垂尾抖振控制中多重動力吸振器設計

牛文超，李　斌

垂尾抖振控制中多重動力吸振器設計

牛文超，李斌

（西北工業大學 飛行器結構力學與強度技術國防重點學科實驗室，西安 710072）

針對飛機垂尾抖振抑制的需要，進行小型電渦流耗能動力吸振器設計，并推導多重動力吸振器最優參數設計方法。分別以懸臂梁系統和縮比垂尾為被控對象，并考慮動力吸振器與垂尾實際尺寸，選定合理安裝位置，通過有限元仿真驗證多重動力吸振器吸振性能，仿真結果表明多重動力吸振器具有良好的振動抑制效果，可滿足設計預期要求。

振動與波；抖振抑制；電渦流阻尼力；多重動力吸振器；有限元；優化設計參數

當飛機進行高機動性飛行時，垂尾時常處于不穩定渦流中并產生抖振現象，激起結構的彎扭模態振動，使飛機結構出現振動疲勞問題。動力吸振器是結構振動控制最常見的手段之一，它一般分為主動型、被動型、半主動型、混合型四種形式。主動可調型動力吸振器系統復雜，受成本高、可靠性差、適航性等制約，目前應用范圍有限。而被動式動力吸振器作為最常見的形式具有原理和結構簡單、可靠性和穩定性高、不需要外界提供能量等特點，在實踐中得到廣泛的應用。

動力吸振器最早可追溯到1940年，在主結構上連接一個中等質量的振子后，主結構在共振頻率附近的共振峰值明顯降低。Clark最早研究應用多重動力吸振器在較寬的頻帶內控制結構振動，并且每個吸振器都在不同的頻率上起作用［1］。此后，研究者陸續關注多重動力吸振器在單自由度主結構中的應用，并驗證了多重動力吸振器的有效性［1］。目前多重動力吸振器在土木建筑或大型機械結構的應用研究較多，在航空結構的應用研究則較少。

飛機設計對重量限制非常嚴格，另外飛機垂尾內部空間極為有限，因此用于飛機垂尾抖振抑制的動力吸振器必須滿足小型化和輕量化的設計要求。電渦流耗能動力吸振器具有良好的可設計性，阻尼、剛度、質量可以方便地靈活調節，為實現動力吸振器的小型化和輕量化設計提供了一個有效的手段。本文將在前期所研制小型化電渦流耗能動力吸振器的基礎上，進一步研究多重小型電渦流耗能動力吸振器在垂尾抖振抑制中的可行性。

1　電渦流耗能動力吸振器簡介

本文提出的電渦流耗能動力吸振器空間布局緊湊、基于非接觸式電渦流耗能機理、阻尼可設計，并實現剛度和阻尼的完全分離，如圖1所示。采用磁鐵在銅管內運動的布局形式，通過導體切割磁感線，在導體內部產生電渦流，形成電渦流阻尼。實際尺寸為長90 mm左右，外徑45 mm左右，吸振器運動質量可在350 g～600 g之間調節，該電渦流吸振器的阻尼調節范圍為2 Ns/m～20 Ns/m。

圖1　電渦流耗能動力吸振器

2　多重動力吸振器設計方法

對于超過二重的多重動力吸振器很難應用定點理論，需要探索新的方法來進行最優調整［4］。如圖2所示，在由質量M與剛度K構成的主振系統上，施加外激勵f，并且在其上設置有n個動力吸振器，吸振器質量、剛度、阻尼分別為mi、ki、ci（i=1，2，…，n）。則力學模型的運動方程為

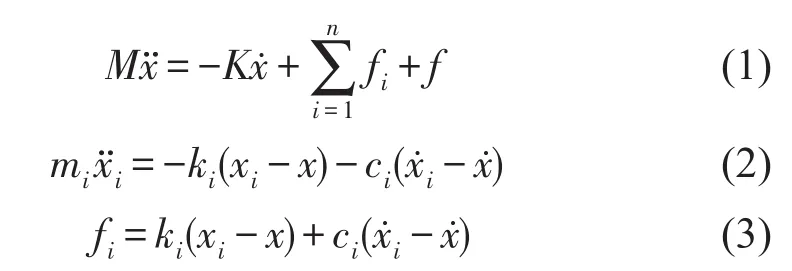
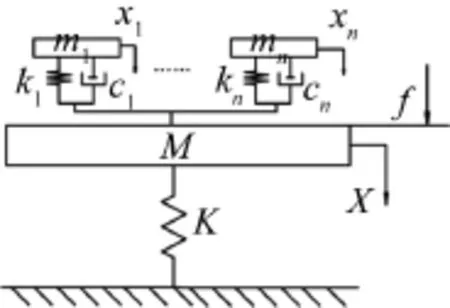
圖2　多重動力吸振器的力學模型

在此定義

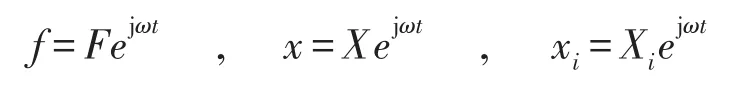
主振系統上的外激勵力F與K的比值F/K定義為靜變形Xst，并引入以下無量綱參數。

利用以上定義，位移振幅比可表示為

其中

n重動力吸振器主振動系統的位移振幅曲線上存在n+1個極值點。根據這些極值峰定義以下兩個評價函數

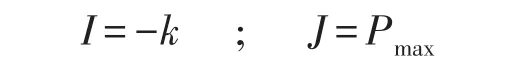
式中k為峰值個數，J為峰值的最大值。本文采用遺傳算法調節多重動力吸振器的最優參數γi（最優同調）、ζi（最優阻尼）使得上述評價函數為最小值。

3　等效懸臂梁的吸振設計分析

首先，以一個與飛機垂尾動力學模型等效的懸臂梁結構為對象，進行多重動力吸振器的性能研究。該等效懸臂梁模型的當量剛度、質量及阻尼取自文獻［7］提供的F18飛機的參考數據，一彎等效質量、剛度、阻尼系數和固有頻率分別為

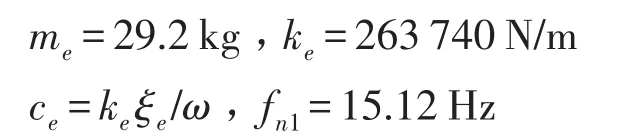
實際設計的等效懸臂梁模型如圖3所示，懸臂端長為901.4 mm、寬為137.6 mm、厚為30 mm，端部配重質量為22.315 kg，材料為45號鋼。通過模態分析得到該懸臂梁系統的1階彎曲固有頻率為15.201 Hz，與垂尾模型1階彎曲固有頻率的誤差為0.54%，由此可見該懸臂梁系統的剛度和質量可以較好地模擬垂尾的1階振動。

圖3　等效懸臂梁模型

四重吸振器的優化設計參數

十重吸振器的優化設計參數

針對設計結果，進行有限元仿真，并與單重動力吸振器的吸振效果進行對比，如圖4所示。由圖可以看出，具有最優參數設計的多重動力吸振器吸振效果明顯增強，吸振器作用頻帶寬度增加，重數越高吸振器效果越好，并不斷趨近于一個最優值。另外需要指出的是，多重吸振器如果簡單地處理為多個質量、剛度和阻尼相等的小吸振器，其效果與單一大吸振器的效果是相同的。因此進行多重吸振器的優化設計是非常必要的。對本例，與單一大動力吸振器方案的最大位移振幅比相比，四重動力吸振器共振峰減少16%，十重動力吸振器減少20%。

圖4　多重動力吸振器吸振效果對比

4　垂尾吸振設計分析

為進一步分析多重動力吸振器對垂尾的吸振效果，以某戰機的縮比垂尾模型為對象進行動力吸振器優化設計分析，垂尾模型如圖5所示。參照垂尾內部安裝空間尺寸與動力吸振器的實際尺寸，選定圖5所示的吸振器安裝點為參考點，可推導出對應1階彎曲振型的垂尾等效模型的模態質量、模態剛度分別如表1所示。

表1　垂尾等效單自由度動力學模型參數

圖5　垂尾模型

進一步確定動力吸振器參數，選取3號點為單一動力吸振器安裝點，通過有限元分析可以得到垂尾最大位移響應與動力吸振器質量的關系，結果如圖6所示。可以發現，垂尾的最大位移響應隨動力吸振器質量增加而減少，且曲線斜率逐漸降低。當動力吸振器質量大于1.7 kg時，曲線斜率變為最小且保持不變。考慮到輕型化的設計要求，選定動力吸振器質量為1.7 kg。

圖6　垂尾最大位移響應與吸振器配重的關系

分別對垂尾安裝單一動力吸振器、未安裝動力吸振器和安裝四個動力吸振器等工況進行了有限元仿真分析。計算過程中激勵點的響應拾取點如圖5所示，激勵為單位激勵。首先，對比未安裝動力吸振器與安裝單一動力吸振器兩種工況下的垂尾端部的位移頻率響曲線，結果如圖7所示。未安裝動力吸振器垂尾端部的最大位移為2.44 mm，安裝單一動力吸振器的最大位移為0.197 mm，垂尾的最大減幅比為92%。

圖7　單位激勵激起的頻率響應

下面進一步研究多重動力吸振器的吸振性能，上節中限定了吸振器的總質量元素為1.7 kg。參照電渦流動力吸振器的實際參數，本文采用四個動力吸振器進行分析，每個吸振器質量為0.425 kg。將四個動力吸振器分為三種不同的工況：

（1）以其中一點為參考點確定動力吸振器剛度阻尼參數，四個動力吸振器參數完全相同。

（2）四點分別作為參考點確定各自的動力吸振器參數。

（3）以其中一點為參考點，采用上節方法得到的多重動力吸振器的最優設計參數矩陣，確定吸振器剛度、阻尼參數。

對比上述三種工況下的垂尾端部的位移頻率響應曲線，結果如圖8所示。工況一的最大位移響應為0.334 mm、工況二的最大位移響應為0.285 mm、工況三的最大位移響應為0.165 mm。工況三的最大減幅比為93.24%。由此可見，若滿足多重動力吸振器的最優設計參數時，吸振器的吸振效果明顯增強，吸振頻帶增寬。

圖8　多重方案的頻率響應對比

如圖9進一步給出了單一大動力吸振器與最優四重動力吸振器之間的結果對比，四重動力吸振器的響應峰值比單重方案降低16.2%，與等效懸臂梁算例效果相當。

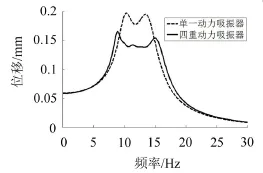
圖9　單重與四重方案的對比

5　結語

針對垂尾抖振抑制的需要，提出利用電渦流耗能動力吸振的設計參數可分離設計，及便于小型化等特點，開展了多重動力吸振的優化設計方法研究。

分別以等效懸臂梁模型和垂尾模型為例，參照所設計的電渦流耗能動力吸振器的具體參數，通過有限元仿真分析驗證了多重動力吸振器在等效懸臂梁模型和垂尾模型中的吸振效果。分析結果表明，符合最優參數設計的多重動力吸振器的吸振效果明顯，并且吸振效果要高于單一大吸振器方案。相關研究結果可為進一步的工程實用設計提供有益參考。

［1］HOUSNER G W，BERGMAN LA，CAUGHEY T K，et al. Structural control：past，present，and future［J］.ASCE Journal of Engineering Mechanics，1997（123）：897-971.

［2］JANGID R S.Dynamic characteristics of structures with multiple tuned mass dampers［J］.Structural Engineering and Mechanics，1995（3）：497-509.

［3］JANGID R S，DATTA T K.Performance of multiple tuned massdampersfortorsionallycoupledsystem［J］. Earthquake Engineering and Structural Dynamics，1997（26）：307-17.

［4］張炳康，何立東，楊秀峰.顆粒碰撞環形調諧質量阻尼器的設計與實驗［J］.噪聲與振動控制，2014，34（4）：142-147.

［5］李斌，牛文超，徐兆懿.電渦流耗能動力吸振器設計與試驗研究［J］.西北工業大學學報，2016，34（1）：18-24.

［6］背戶一登.動力吸振器及其應用［M］.北京：機械工程出版社，2013：1-2.

［7］JOSEPHRMALY，KEVINL.NAPOLITANO.A magnetic tuned mass damper for buffet-induced airfoil vibration［EB］//http www.csaengineering.com，2010.

Design of Multiple Dynamic VibrationAbsorbers for Buffet Control of Vertical Tails

NIU Wen-chao，LIBin
（Fundamental Science onAircraft Structural Mechanics and Strength Laboratory，Northwestern Polytechnical University，Xi'an 710072，China）

Aiming at the need of vertical tail buffet suppression，the eddy current vibration absorber is designed and its parameters is introduced.The optimal design parameters method of the multiple dynamic vibration absorber is deduced to realize the vibration absorber miniaturization.Taking an equivalent cantilever beam system and a scaled vertical tail as the objects respectively for vibration control，considering the actual size of the vibration absorber and the vertical tail，and choosing the reasonable installation position，the vibration absorption effect of the multiple-dynamic-vibration-absorber is verified through the finite element simulation.Simulation results show that the vibration suppression property of the multiple-dynamic-vibration-absorber scheme is very good.Compared to the single large dynamic vibration absorber，the vibration attenuation rate of the quadruple dynamic vibration absorber scheme is increased by 16%，and will be raised by 20%for the ten-dynamic-vibration-absorber scheme.

vibration and wave；buffet suppression；eddy current damping force；multiple dynamic vibration absorber；finite element；optimal design parameters

V214

ADOI編碼：10.3969/j.issn.1006-1335.2016.03.040

1006-1355（2016）03-0197-04

2015-10-20

國家自然科學基金資助項目（11172238）；中央高校基本科研業務費專項資金資助項目（3102014KYJD015）

李斌（1975-），男，湖北咸寧人，教授，博士生導師，主要研究方向為結構動力學與控制。E-mail：leebin@nwpu.edu.cn