STAP抗混響輔助樣本的選取方法

趙申東, 周田宰, 沈建森

?

STAP抗混響輔助樣本的選取方法

趙申東, 周田宰, 沈建森

(海軍航空工程學院青島校區, 山東青島, 266041)

空時自適應處理(STAP)的一個關鍵問題是協方差矩陣的估計, 協方差矩陣的估計是依靠待檢數據附近的輔助樣本來完成的。要使估計精度足夠高, 就要求獲取足夠多的獨立同分布的輔助樣本。文中對混響數據輔助樣本的相關性、同分布特性、時間點數選擇問題進行了分析, 根據水聲信號的特點, 給出了有效的處理方案。通過綜合考慮協方差矩陣估計精度、自適應處理運算量和降維STAP方法等因素, 給出了采用STAP方法抑制混響時輔助樣本的選取方法, 為STAP抗混響的實現提供了條件。

水聲信號; 抗混響; 空時自適應處理(STAP); 輔助樣本

0 引言

空時自適應處理(space time adaptive processing, STAP)是抑制機載雷達雜波的一種有效方法。Klemm[1]分析了聲吶混響和雷達雜波的相似性, 指出可以采用空時自適應濾波器進行混響的抑制; Jaffer[2]設計了將STAP用于混響抑制的方案; 文獻[3]提出采用梳狀譜信號用來改善探測的時域分辨能力, 同時還提出了先時后空的級聯自適應處理方法用來抑制混響; 文獻[4]提出的方法也可視為一種廣義的STAP, 以被動方式確定目標的方位; 文獻[5]將STAP方法應用到拖線陣上, 給出了STAP方法的基本結構, 介紹了全維STAP方法; Pillai[6]等將STAP算法應用到了被動聲吶中, 在空間-頻率域內采用寬帶STAP方法用來增強聲吶對弱運動目標的檢測能力。進行STAP處理的一個關鍵問題就是待檢數據混響協方差矩陣的估計, 而這一估計依靠的是合理選取輔助樣本, 即選擇足夠多的滿足獨立同分布條件的輔助樣本。以上研究表明, STAP用于混響抑制可取得明顯效果, 但均未對協方差矩陣求解方法和標準進行詳細討論。文獻[7]針對協方差矩陣的影響進行了專門研究, 比較了理論導向矢量合成法和直接陣列數據域法2種協方差矩陣計算方法。文章將討論解決如何從混響序列中合理選取輔助樣本這一問題。

1 輔助樣本的相關性

所選擇的輔助樣本要滿足獨立同分布的條件。輔助樣本是通過從待檢數據兩側鄰近的混響數據中選擇與待檢樣本同樣大小的一段空時數據而形成的, 即它們的空間采樣點和時間采樣點都是相同的。如何確定輔助樣本的起始位置是保證樣本間獨立性的關鍵所在。仿真以及試驗數據表明, 混響數據的瞬時值服從高斯分布[8], 所以輔助樣本間的獨立性與不相關是等價的。為此, 可以通過對2個具有一定間隔的輔助樣本之間的相關性檢驗來判斷其是否獨立。

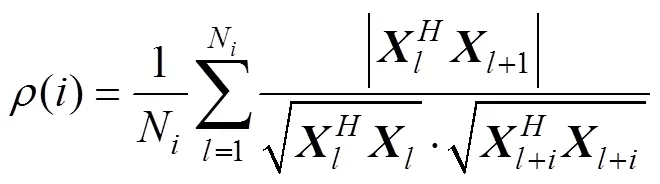
圖1所示的是一組采用典型參數仿真的混響輔助樣本的相關系數, 其中圖(a)為脈寬50 ms的情形, 圖(b)為脈寬100 ms的情形。仿真時采用由12個陣元組成的等距線陣, 陣元間隔為半波長, 基陣的運動速度為40 kn, 線陣軸線方向與基陣運動方向垂直, 即為前視陣情形; 發射信號為20 kHz的單頻信號, 脈寬分別為50 ms和100 ms, 發射波束水平寬度為90°, 主波束指向線陣的法線方向, 即基陣運動的方向; 海深為50 m, 陣列距海底43.5 m, 底質為粘土; 不考慮陣元誤差。

為了盡量減少混響的時間采樣點數以降低STAP的處理維數, 需要對混響信號進行降采樣處理。通常單頻脈沖的聲吶混響為窄帶信號, 首先將其解調得到復包絡, 然后采用較低的采樣率對信號進行重新采樣, 新的采樣率應能保證所有可能出現的混響和目標信號的頻移不會出現模糊, 在此基礎上盡量采用低的采樣率。本仿真的混響復包絡信號采樣率為1 200 Hz, 該采樣率可以保證不同方位的混響頻移不發生混疊, 所以脈寬為50 ms時, 目標的信號包含60個左右的采樣點, 脈寬為100 ms時, 目標的信號包含120個左右的采樣點。圖中不同曲線表示選擇不同點數時輔助樣本的相關系數, 橫坐標表示2個輔助樣本相隔的點數。

通過圖1可以看出, 當2個輔助樣本相隔較近時, 它們具有較強的相關性, 當輔助樣本時間采樣間隔點數增加到6~7個時, 不論樣本的時間點數多于還是少于發射脈寬對應的采樣點數, 其相關系數基本已經降到了0.3以下, 可以認為2個輔助樣本已經不相關。如果所選的時間采樣間隔點數太少, 輔助樣本間具有一定的相關性, 進行協方差估計時要想達到同樣的精度, 就需要更多的樣本數。

同時還可以發現, 當發射脈寬不一樣, 而其他條件相同時, 圖1(a), (b)兩圖中相關系數是稍有區別的, 脈寬為100 ms的相關系數要稍大于脈寬為50 ms的相關系數。這是因為發射脈寬增大后, 所有混響散射元的散射信號都會相應拖長, 總的混響時間相關性增強, 所以相同間隔的2個輔助樣本相關性也會相應增強。所以, 在給定的混響序列中, 只要2個輔助樣本間隔足夠大, 就可以認為它們是相互獨立的。當然, 樣本間隔太大也是不可取的, 因為那樣會使得從相同長度的混響中取得的輔助樣本數量變少, 不利于協方差矩陣的準確估計。通過仿真計算, 可以得出如下結論: 2個輔助樣本的相關系數降至0.3左右時, 此時2個樣本的間隔點數是比較合適的選擇。

2 輔助樣本的同分布問題

在估計協方差矩陣時, 如果輔助樣本不是同分布的, 或者說它們的統計特性是明顯不同的, 那么即使獨立的樣本數再多也不能準確反映出混響的分布特性, 也就難以求解出有效的加權系數, 所以輔助樣本的同分布是STAP協方差矩陣估計中一個重要條件。

文獻[9]提出了一種采用關聯維數的大小來評判樣本間數據是否相似的方法。樣本關聯維數的差別表明了樣本的相似程度或逼近程度, 2個樣本的統計特性越相似, 它們的關聯維數也就越接近, 可以用樣本的關聯維數作為剔除非均勻輔助樣本的依據。關聯維數的求取方法如下。

(3)

圖2給出的就是位于不同時刻的仿真混響輔助樣本的關聯維數。仿真時, 發射信號脈寬為100 ms, 采樣率為1200Hz, 輔助樣本的時間采樣點數為120, 其他參數與圖1中的參數一樣。

從圖2可以看出, 不同時刻的輔助樣本關聯維數總體變化趨勢是在逐漸增大, 這說明在短時間內輔助樣本的統計特性是相近的, 而在較長時間內其統計特性逐漸發生了變化, 偏離了同分布的條件。所以, 如何選擇合適的混響時間長度就成了問題的關鍵所在。

合適的長度應該使得所選的混響既能保證樣本的統計特性不發生較大變化, 又能提供足夠的樣本用來進行協方差矩陣的估計。但是, 從圖中還可以看出, 這些樣本的關聯維數存在較大的起伏振蕩, 難以據此準確界定混響非均勻的范圍, 所以需要依據其他的標準進行判定。實際上, 選擇接收信號的功率作為均勻混響范圍的判定標準是比較合適的。這是因為在平坦的淺海條件下, 混響的主要來源是海底, 不同時刻海底的散射元都是呈圓環形分布, 散射元分布情況是相似的, 所以不同時刻混響譜在空時2D平面上的分布也是相似的, 主要的差別就是混響功率與噪聲功率比值的大小發生變化, 而這一變化就意味著輔助樣本的統計特性發生了變化。噪聲功率在整個接收過程中基本是不變的, 所以接收信號功率的變化就體現了混響功率的變化, 同樣也體現出了輔助樣本統計特性的變化。結合混響的衰減規律, 這里選擇功率衰減在6 dB~10 dB以內的信號作為輔助樣本的選取范圍。

盡管這樣選取的混響輔助樣本并非嚴格滿足同分布的條件, 但為了取得足夠數量的輔助樣本, 就不得不放松對該條件的要求, 在統計特性和混響長度上進行適當折衷。在距離較近的混響處, 由于混響衰減較快, 為了得到足夠的樣本數量, 可以將起止混響的功率差選為10 dB, 這樣在10 kHz~20 kHz范圍內, 在750 m附近的混響用于估計協方差矩陣的數據時間長度約為0.4 s; 在距離較遠的混響處, 混響衰減較慢, 可以將起止混響的功率差選為6 dB, 這樣在1500 m附近用于估計協方差矩陣的混響時間長度約為1 s。

3 輔助樣本時間采樣點數的確定

選定均勻混響的分布范圍和相鄰輔助樣本的間隔后, 還需要確定單個輔助樣本中的時間采樣點數才能最終給出所有用于協方差矩陣估計的輔助樣本。單個輔助樣本時間采樣點數越少, 則進行STAP處理的維數就越低, 運算量也就越小。但是, 較少的采樣點數也會帶來不利的影響。輔助樣本的大小與待檢數據的大小相一致, 減少輔助樣本的時間采樣點數也就意味著減少了待檢樣本的時間點數, 這首先會降低STAP處理器的頻率分辨率。除此以外, 時間采樣點數太少也不利于提高輸出信號的信混比, 下面的仿真就說明了這一點。

圖3給出的是輔助樣本選用不同的時間點數時, STAP處理器的改善因子。仿真時, 發射信號脈寬為50 ms, 采樣率為1200 Hz, 所以1個脈寬對應的信號時間采樣點數為60, 其他參數與圖1中的參數一樣。圖中所求的改善因子都是假設目標位于基陣運動的正前方, 即主波束照射的方向, 目標的運動速度為5 kn, 運動方向遠離基陣。待檢數據位于脈沖發射后的2.2 s處, 用于估計協方差矩陣的混響位于待檢數據的左右兩側, 兩側的時間長度各取為0.5 s, 相鄰輔助樣本的時間點數為5。通過如上參數可以大概估計出所能得到的輔助樣本的數量, 當單個輔助樣本時間點數從10增加到100時, 輔助樣本的數量從238個降到202個。可以發現, 這些輔助樣本不能全部滿足進行全維STAP處理的條件, 但是都可以采用一種降維的處理方法進行計算—局域聯合處理(joint- domain localized, JDL)[10]。

在采用JDL方法進行處理時, 方位方向取5個輔助波束, 多普勒方向取5個輔助波束, 降維后的系統自由度為25。觀察圖中的改善因子可以發現, 在少于1個脈寬對應的點數60時, 隨著輔助樣本時間點數的增加, 處理器的改善因子隨之增加。這是因為待檢數據時間點數越多, 說明利用的目標回波越充分, 檢測輸出中目標信號的強度也就越大。但是當輔助樣本時間點數超過1個脈寬所對應的點數時, 改善因子反而隨著時間點數的增加而降低。這是因為點目標的信號信息已經被全部利用, 此時再增加時間點數, 反而會增加混響能量的輸出, 降低了輸出信混比。所以, 選擇輔助樣本的時間點數時, 應該在輔助樣本數量能夠滿足協方差矩陣估計精度的前提下, 選取與發射脈寬相一致的時間點數。

4 結束語

綜上所述, 混響輔助樣本的選取需要兼顧樣本長度、統計特性和樣本數量, 而這些參數又是相互影響、相互制約的。當采用STAP方法進行混響抑制時, 需要對這幾個參數進行綜合的權衡折中, 同時還要考慮盡量降低系統的運算量。

通常當2個輔助樣本的相關系數降至0.3左右時, 可以認為此時樣本已經滿足獨立性的要求; 選擇混響信號的功率作為均勻混響范圍的判定標準是比較合理可行的一種方案; 輔助樣本時間點數的選擇需要考慮樣本數量能否滿足協方差矩陣估計的要求, 若能夠保證, 則應選取與發射脈寬相一致的時間點數, 否則應該根據輔助樣本的實際數量來降低樣本的時間點數。

需要指出的是, 文中判斷輔助樣本獨立性的相關系數是在特定海洋環境及發射參數下給出的, 當參數改變后, 相關系數的取值也應略有不同, 需要進行進一步的研究。

[1] Klemm R. Interrelations Between Matched-field Processing and Airborne MTI Radar[J]. IEEE Journal of Oceanic Engineering, 1993, 18(3): 168-180.

[2] Jaffer A G. Constrained Partially Adaptive Space-time Processing for Clutter Suppression[C]//28th Asilomar Conference on Signal, System and Computer, Pacific Grove, CA, 1994: 671-676.

[3] Mio K, Chocheyras Y, Doisy Y. Space Time Adaptive Processing for Low Frequency Sonar[C]//Oceans Conference Record (IEEE), USA, 2000: 1315-1319.

[4] Kim B C, Lu I T. High Resolution Broadband Beamforming Based on the MVDR Method[C]//IEEE Oceans Conference, 2000: 1025-1028.

[5] Maiwald D, Benen S, Hostermann H, et al. Space-time Adaptive Processing for Active Towed Array Sonar Systems[C]//UDT Europe 2001, 2001: 1-6.

[6] Pillai S U, Guerci J R, Pillai S R. Wideband STAP (WB- STAP) for Passive Sonar[C]//Oceans 2003. Proceedings, 2003: 2814-2818.

[7] 呂維, 王志杰, 李建辰, 等. 混響空時協方差矩陣的兩種計算方法比較與分析[J]. 魚雷技術, 2012, 20(4): 251-255.Lü Wei, Wang Zhi-jie, Li Jian-chen, et al. Comparison and Analysis of Two Calculation Methods of Space Time Co- variance Matrix for Reverberation[J]. Torpedo Technology, 2012, 20(4): 251-255.

[8] 趙申東, 唐勁松, 蔡志明. 多通道運動聲吶混響仿真[J]. 艦船科學技術, 2007, 29(4): 117-120.Zhao Shen-dong, Tang Jin-song, Cai Zhi-ming. Simulation of Multi-channel Moving Sonar Reverberation[J]. Ship Science and Technology, 2007, 29(4): 117-120.

[9] 陳建文, 王永良, 皇甫堪, 等. 基于非均勻檢測的機載雷達空時自適應處理方法[J]. 數據采集與處理, 2000, 15(1): 44-47.Chen Jian-wen, Wang Yong-liang, Huang Fu-kan, et al. The STAP Method of Airboarn Radar Based on Inhomogeneous Detection[J]. Data Acquisition and Processing, 2000, 15(1): 44-47.

[10] Wang H, Cai L. On Adaptive Spatial-temporal Processing for Airborne Surveillance Radar Systems[J]. IEEE Trans. AES, 1994, 30(3): 660-670.

(責任編輯: 陳 曦)

Selection of Auxiliary Samples for Reverberation Suppression via STAP

ZHAO Shen-dongZHOU Tian-zaiSHEN Jian-sen

(Qingdao Branch, Naval Aeronautical and Astronautical University, Qingdao 266041, China)

A key link in space-time adaptive processing (STAP) is the estimation of covariance matrix, which depends on auxiliary samples near the sample to be detected. To ensure the estimation accuracy, sufficient independent identically distributed auxiliary samples are necessary. In this paper, the correlation of reverberation auxiliary samples, the identical distribution characteristic, and the selection of time point number are analyzed, and a corresponding valid scheme is given according to the characteristics of acoustic signal. As a result, a selection method of auxiliary samples for reverberation suppression via STAP is proposed through comprehensively considering the estimation precision of covariance matrix, the operand of adaptive processing, and the dimension-reduced STAP.

acoustic signal; reverberation suppression; space-time adaptive processing(STAP); auxiliary sample

10.11993/j.issn.1673-1948.2016.06.004

TJ630.3; TN911.2

A

1673-1948(2016)06-0417-05

2016-08-26;

2016-10-27.

趙申東(1978-), 男, 副教授, 主要研究方向為水聲信號處理.