采用兩步式模型修正過程識別海上風電支撐結構的損傷

李英超，張 敏，王樹青

(1.魯東大學 土木工程學院，山東 煙臺 264025；2.中國海洋大學 工程學院，山東 青島 266100)

采用兩步式模型修正過程識別海上風電支撐結構的損傷

李英超1，張 敏2，王樹青2

(1.魯東大學 土木工程學院，山東 煙臺 264025；2.中國海洋大學 工程學院，山東 青島 266100)

針對海上風電支撐結構損傷識別的難點，將一種新的模型修正方法應用到了三腳架式海上風電支撐結構的損傷識別中。采用數學上常用的正則化方法，解決了實測模態含噪聲條件下損傷識別“病態”方程組的求解問題；結合Guyan擴階技術，實現了基于低階不完備模態的損傷識別。另外，為提高損傷識別精度，結合算例提出一種兩步式模型修正過程：第一步，初步定位損傷位置；第二步，精確識別損傷位置和損傷程度。數值研究結果表明，采用兩步式模型修正過程的方法對于海上風電支撐結構的損傷識別是有效的。

損傷識別； 模型修正； 海上風電；正則化；模態擴階

Abstract:Through a numerical example,a recently developed model updating method is applied to identify the damages of the tripod-type offshore wind turbine support structure.Regularization method of mathematics is used to solve the “ill-conditioned” damage identification equations when noise polluted measured modes are used.With Guyan expansion technology,damage identification is realized based on a few low order incomplete modes.Moreover,in order to improve the accuracy of damage identification,a two-step model updating process is proposed.The first step is to locate damage position.The second step is to identify damage location and damage severity accurately.Results of numerical examples show that the method used in this paper is effective for damage identification of offshore wind structure.

Keywords:damage identification; model updating; offshore wind turbine; regularization; modal expansion

海上風電支撐結構長期作用在復雜的海洋環境中，除了要承受風機荷載外，還將受到波浪、流、風，甚至冰擊、船的撞擊和臺風、地震等極端荷載的作用，另外結構本身還要遭到環境腐蝕、海生物附著、海底沖刷、復雜海床變化等影響。在此環境下，結構容易產生各種各樣的損傷，使得結構整體動力特性發生改變，嚴重時還會導致結構失效，造成巨大的經濟損失和不良的社會影響。為了合理有效地維護海上風電結構，減少因結構損傷導致的風機停機時間，降低維護成本，采用有效的方法對風電結構在服役期內的安全性進行實時監測或定期檢測是非常必要的[1]。

然而，海上風電支撐結構大部分位于水面以下和泥面以下，且常以建筑群的形式存在，測試非常困難，傳統的無損檢測方法很難進行應用。與此相反，基于振動測試的結構整體檢測技術日益受到國內外學者的關注，并成為研究的熱點[2]。其基本原理是根據結構的實測動力特性反推結構的物理參數，從而診斷結構的健康性。其最突出的優點是利用環境激勵下的動力響應進行損傷診斷，檢測過程不影響正常使用[3]。

基于振動測試的結構損傷診斷技術在航空航天、土木工程和機械工程等領域得到了深入的研究和廣泛的應用，目前學者們已經提出了多種較成熟的方法，如模型修正法、敏感性分析方法、神經網絡方法、小波包變換法、遺傳算法、頻響函數法和模態應變能法等。但這些方法在海洋結構物中的應用還受到一些限制，如傳感器布置困難，使得實測模態極度不完備；另外環境激勵下的實測信號噪聲污染較大，識別精度較差等。針對這類問題， Hu和Li等[4-5]提出了交叉模型交叉模態(cross model cross mode,簡稱CMCM)有限元模型修正方法，并將其應用于海洋平臺結構的損傷診斷中。相比于傳統方法，CMCM方法最大的優點是可以應用有限的低階實測模態構建更多的線性方程，使得修正因子(損傷程度)更利于求解。然而這種方法在實際應用中存在兩個技術瓶頸：1)實測模態空間不完備問題；2)實測模態含噪聲條件下模型修正“病態”方程組的求解問題[6]。

針對第1)類問題，Li等[5]展開了研究，結合擴階/縮階技術實現了基于低階不完備模態的模型修正。而對于第2)類問題，尚未展開細致研究。線性“病態”方程組的求解問題在數學領域并不罕見，常用的手段是正則化方法。最早的正則化方法由Tikhonov[7]1963年提出，通過正則化參數的選擇，使得求解在最小二乘解和最小范數解之間取得平衡，從而控制解的振蕩和方程的擬合程度。目前最常用的正則化方法主要依據矩陣的奇異值分解(SVD)技術，如截斷奇異值分解(TSVD)方法[8-10]。文獻[11]對各種正則化方法進行了較系統深入的研究，針對中小規模、大規模等不同的“病態”系統提出了適用的正則化方法。研究還指出，利用正則化方法求解不適定問題的關鍵是正則化參數的選擇，這一過程通常需要借助一些數學統計手段，如Morozov偏差準則、廣義交叉檢驗法、“L”曲線法等，這些方法均需要進行大量的試算。正則化方法盡管在理論上比較完善，但在模型修正的實際應用中卻仍然存在一些問題，如對于不同問題，同一算法表現出的收斂性卻不同，很難用一個通用的方法解決不適定問題[12]。

將這種新的模型修正方法(CMCM 方法)應用到海上風電支撐結構的損傷識別中。首先，給出了該方法的推導過程；然后介紹了正則化求解方法和Guyan擴階技術，分別用以解決該方法在測量噪聲影響下存在的“病態”求解問題和實測空間不完備問題；最后，以一個三腳架式海上風電支撐結構為模型進行數值模擬驗證。為提高損傷識別精度，文章結合算例提出一種兩步式模型修正過程，通過第一步模型修正實現對損傷的初步定位；在此基礎上，進行第二步模型修正，從而實現對損傷位置和損傷程度的精確識別。結果表明，在實測模態不完備且含有測量噪聲條件下，結合正則化求解方法和Guyan擴階技術，采用兩步CMCM方法可以準確地識別結構的損傷。

1 基本理論

1.1CMCM方法

將未損傷結構的整體剛度矩陣和質量矩陣記為K和M，一般可通過有限元模型分析得到，其對應于第i階特征值λi和特征向量Φi的關系可表示為

假設損傷結構模型的剛度矩陣記為K*，并將其寫為對未損傷模型剛度矩陣K的一個修正：

其中，Kn為第n個單元在整體坐標系下的剛度矩陣；Ne為待識別損傷單元的個數；αn為剛度修正系數，即損傷程度，可模擬為對應單元的材料彈性模量的變化。另外，假定結構在損傷過程中，不發生質量的變化，即

對于損傷模型，同樣存在特征關系：

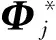
將式(4)前乘Φi的轉置(Φi)T，可得

將式(2)、式(3)代入式(5)得到一線性方程：

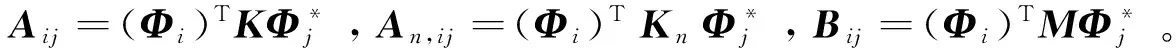
用m代替ij，式(6)改寫為

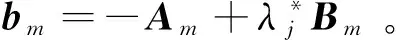
由以上推導過程可以得出，當有Ni階模態從未損傷模型中獲取，并且Nj階模態從損傷結構的模態測試中獲得時，共可以組建Nm=Ni×Nj個形如式(7)的線性方程，將其寫為方程組

其中，A為Nm×Ne的矩陣；x為包含Ne個剛度損傷系數αn的列向量；b為Nm×1的列向量。

求解模型修正方程組(8)即可實現對結構進行損傷定位和損傷程度的識別。由于未損傷模型的模態是通過有限元分析獲得，其可用模態數較多，因此該方法所構建的方程組通常屬于超定情況， 即Nm≥Ne，此時可采用奇異值分解法來求取方程組的最小二乘解。

對式(8)的系數矩陣A做奇異值分解：

其中，U∈Nm×Nm，V∈Ne×Ne為酉矩陣，Σ∈Nm×Ne為奇異值矩陣。 由于矩陣A的某些奇異值可能為0，因此奇異值矩陣Σ可寫為

其中，對角陣Σr=diag(σ1,σ2,…,σr)的對角元素為矩陣A的奇異值，且滿足σ1≥σ2≥…≥σr>0，r為A的秩。

將酉矩陣U和V分別記為U=(u1,u2,…,uNm)，V=(v1,v2,…,vNe)，其中u1,u2,…,uNm和v1,v2,…,vNe分別為酉矩陣U和V的列向量，則式(10)可寫為

方程(8)的解可寫為：

1.2正則化求解方法

Tikhonov[7]將最小二乘解和最小范數解綜合考慮：

其中，Γ為正則化矩陣，很多情況下取Γ=I或Γ=αI，其中α稱為正則化參數，用于控制最小二乘解和最小范數解之間的平衡，當α值較大時，可以保證‖x‖值較小，但可能會使得解不滿足方程組Ax=b；反之，如果α值較小，式(13)較接近原問題，雖然能滿足方程組的解，但該解會發生振蕩，使得沒有物理意義。α的取值對求解非常關鍵。

假定A的奇異值分解為式(9)，則方程組(8)的正則解可寫為

稱為正則化因子，其作用是過濾掉小奇異值對解的貢獻，從而起到穩定解的作用。為方便計算，在截斷奇異值分解法(TSVD)中，直接舍棄式(12)中的小奇異值。即取過濾因子為：

如果取σ1≥…≥σk≥α≥σk+1≥…≥σr≥0，則正則解為

其中，k稱為截斷數，當k=rank(A)時，式(17)即為式(12)所示最小二乘解。

利用正則化方法求解病態方程組的關鍵是選擇正則化參數。對于正則化參數α∈(0,∞)或k∈(1,r)，曲線(ln(‖Γx‖2)，ln(‖b-Ax‖2))形狀呈“L”型，稱為“L-曲線”，其角點正好使得最小二乘解和最小范數解得到平衡。因此可以通過該曲線的最大曲率來確定角點，從而確定截斷數k。

1.3Guyan擴階

受海上工作環境的限制，在實際測試中，傳感器布置數目非常有限，這導致實測模態信息往往是空間不完備的。采用Guyan方法對實測模態進行擴階處理。

將結構自由振動方程寫為

其中，下標m表示主自由度(測試自由度)，s表示從自由度(未測試自由度)。忽略慣性力，有

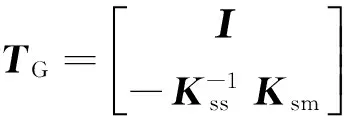
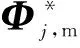
1.4模態應變能法

為驗證方法的優越性，擬采用模態應變能法[13]進行對比研究，基本公式如下：

對于含有ne個單元的線性無阻尼系統，結構的第i階模態應變能定義為：

第j個單元的第i階模態應變能分量寫為：

當有nm階實測模態時，第j個單元的損傷指標βj可以寫為：

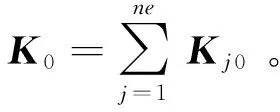
當αj<0時，表示第j個單元有損傷。

2 兩步式模型修正過程

當實測模態空間不完備且包含測量噪聲時，振型擴階和正則化求解過程難免會造成求解誤差，該誤差將隨著實測模態的不完備程度和噪聲水平的提高而增大，因此，單純地采用CMCM方法進行一次模型修正難免會造成損傷的誤判。通過大量試算，結合CMCM方法，提出一種兩步式模型修正過程來精確識別結構損傷。

第一步：將結構的全部單元選為損傷識別(修正)對象，利用CMCM方法構建方程組，根據求解結果，結合物理意義，初步定位損傷位置；

第二步：將初步定位損傷的單元選為損傷識別(修正)對象，利用CMCM方法再次進行識別。根據本次結果通常可以較準確地識別損傷位置和損傷程度。

3 數值算例

3.1算例介紹

一個3.0 MW的海上風電裝置，采用三腳架式(tripod)基礎結構，如圖1所示。應用Matlab編程，建立該風電結構的有限元簡化模型，如圖2所示，共22個單元，17個結點，桿件采用兩結點三維梁單元；結點13和17處分別施加6 t和111 t的集中質量，分別模擬工作平臺處設備和塔頂風機的質量。樁基采用等效固定樁來模擬，等效樁底距泥面的長度取為10 m[14-16]。結構材料為鋼材，彈性模量取為E=2.1×1011N/m2，密度ρ=7 850 kg/m3，采用集中質量矩陣。

通過特征值分解，得到有限元基準模型的模態參數，如圖3所示，其前六階頻率分別為：0.568 5 Hz、0.569 4 Hz、2.787 3 Hz、2.790 2 Hz、5.023 7 Hz和5.034 Hz。

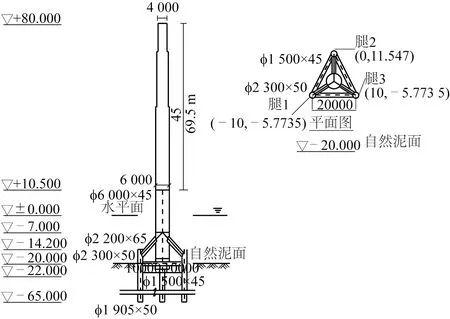
圖1 三腳架式海上風電支撐結構Fig.1 Tripod offshore wind turbine structure

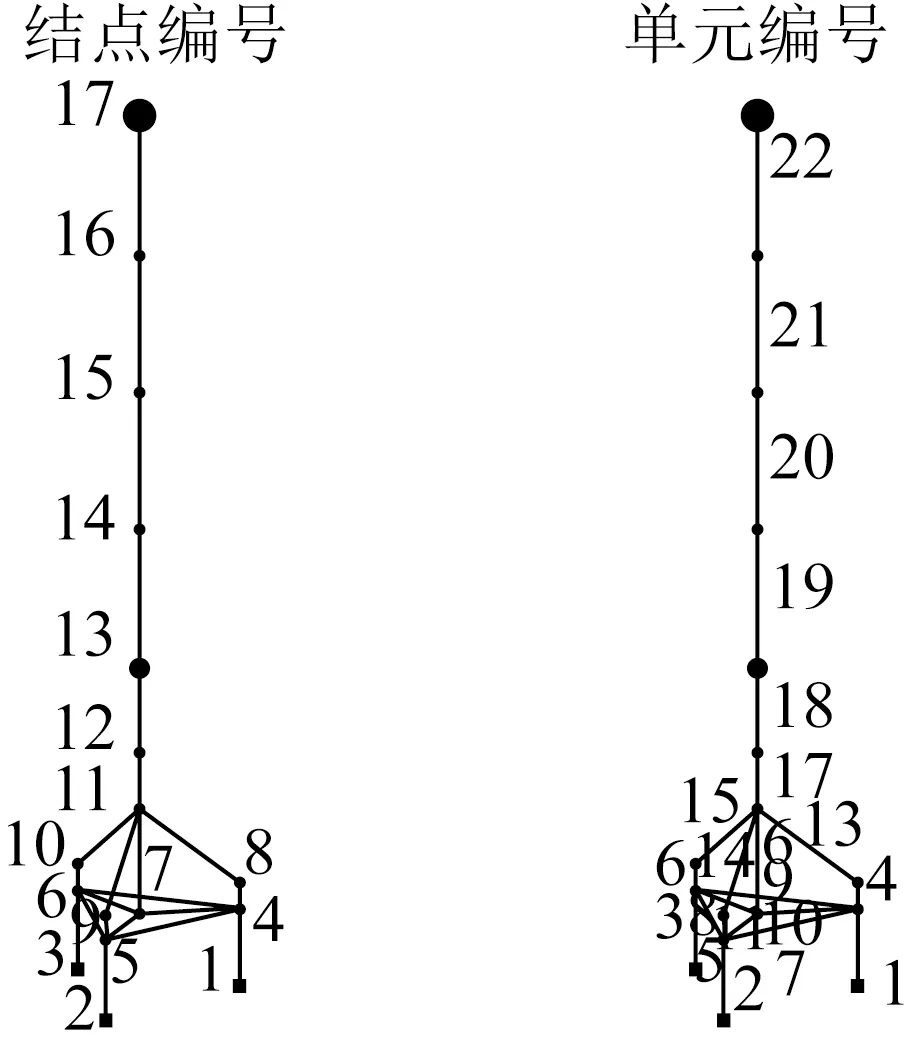
圖2 結構的有限元簡化模型Fig.2 FE model of the structure

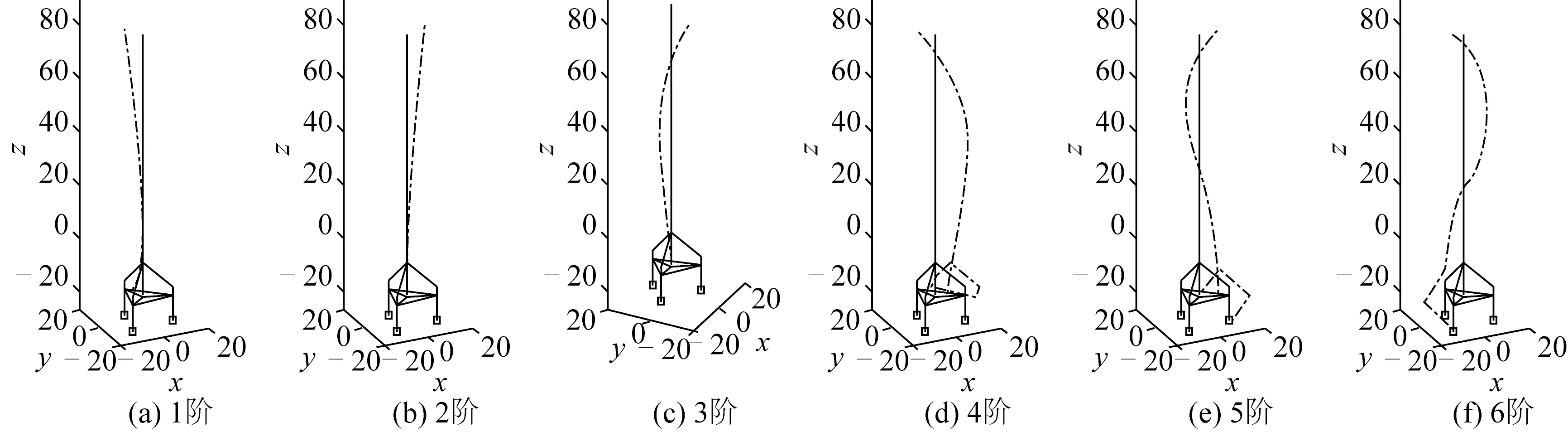
圖3 有限元模型的前六階模Fig.3 The first six modes of FE model

3.2損傷模擬

在本研究中，損傷程度定義為某個構件或單元的剛度損失百分比。比如單元13損傷了20%，即該單元的損傷后剛度比基準模型減少了20%。在該算例中，假定3個單元發生了損傷，分別為三腳架一斜撐(單元13)，水面附近立柱(單元17)，塔架靠近工作平臺段(單元19)，損傷程度均設為30%。損傷結構是通過修改有限元模型中這3個單元的剛度矩陣來進行模擬的，通過特征值分解，得到損傷模型的模態頻率和振型來模擬實測模態參數。損傷模型的前六階頻率分別為：0.520 5 Hz、0.525 5 Hz、2.691 9 Hz、2.733 5 Hz、4.927 9 Hz和4.938 Hz，與損傷前結構相比，頻率均有所降低。

3.3損傷識別

3.3.1 工況1：振型空間完備且不含噪聲

為驗證CMCM方法的適用性，首先假定通過振動測試可以得到損傷結構的前6階模態，振型空間完備，且不含測量噪聲。

將全部22個單元作為損傷識別對象，即Ne=22，利用前6階實測模態和前6階有限元模態，可構建Nm=36個CMCM方程。此時方程個數大于未知數個數，為超定方程，采用奇異值分解法(SVD)求取其最小二乘解，結果如圖4所示，損傷位置和損傷程度均可實現準確的識別。

3.3.2 工況2：振型空間完備且包含噪聲

在實際模態測試中，模態頻率的識別結果一般較準確，而振型的識別結果常常受測量噪聲的影響較嚴重，因此在本算例中假定實測模態振型含有噪聲。噪聲添加方式為Φi,j=Φi,j(1+εRi,j)。其中，ε為噪聲水平，Ri,j為均值為0、方差為1的高斯隨機數，Φi,j為對應于第i個自由度的第j階振型值。即在通過數值模擬獲得的實測模態振型的基礎上添加一定水平的高斯白噪聲。

首先假定噪聲水平為ε=0.5%。同樣將全部22個單元作為損傷識別對象，利用前6階實測模態和前6階有限元模態，構建36個CMCM方程。由于該方程組的條件數較大(cond(A)=3.582 1×105)，噪聲的存在，使得最SVD求解結果發生振蕩，損傷識別結果失效。因此嘗試采用TSVD正則化方法進行求解，并用“L-曲線”法選取截斷數k。通過大量試算，畫出該系統的“L-曲線”，如圖5所示。將曲線中位于角點左側最靠近的點選為截斷數，此時k=13。根據這一截斷數，利用TSVD方法進行求解，損傷識別結果如圖6(a)所示。單元13、單元17和單元19很明顯可以診斷到損傷，但與之相連的單元18和單元20也識別到較大的剛度損傷。因此需要結合物理意義定位損傷位置。通常當某個單元含有剛度損傷時，與之相連的單元也會有模態能量的變化，即也會診斷出一定的剛度損傷[16]。根據這一原則，可以排除單元20(與該單元相連的單元21并未診斷出損傷)；但單元18是否含有損傷尚不能確定。因此，初步定位損傷單元為單元13、單元17、單元18和單元19。

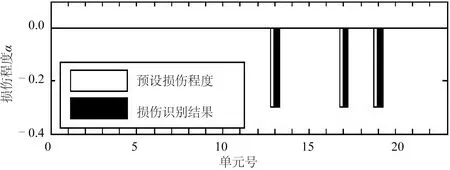
圖4 工況1損傷識別結果Fig.4 Damage identification result of Case 1

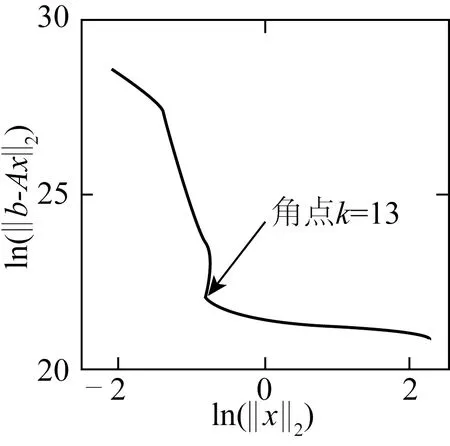
圖5 工況2“L-曲線”圖Fig.5 L-curve of Case 2

將初步定位的四個損傷單元作為識別對象，利用前6階實測模態和前6階有限元模態，重新構建Nm=36個CMCM方程，此時Ne=4。由于此時未知數個數很少，直接采用奇異值分解法(SVD)求取其最小二乘解，結果如圖6(b)所示，在0.5%噪聲影響下，經過第二步識別，可以相當準確的定位出損傷，且對損傷程度的求解誤差也非常小。

圖6 利用兩步式CMCM模型修正方法識別工況2損傷Fig.6 Damage identification with two-step CMCM model updating method of Case 2

為探討該兩步式方法在不同測量噪聲水平下的適用性，將噪聲水平分別設為1%、 5%、10%和20%進行對比研究，如圖7所示。損傷識別方程組的構建方式和噪聲添加方式同上。采用兩步式模型修正過程進行損傷識別，結果如圖8～10所示。

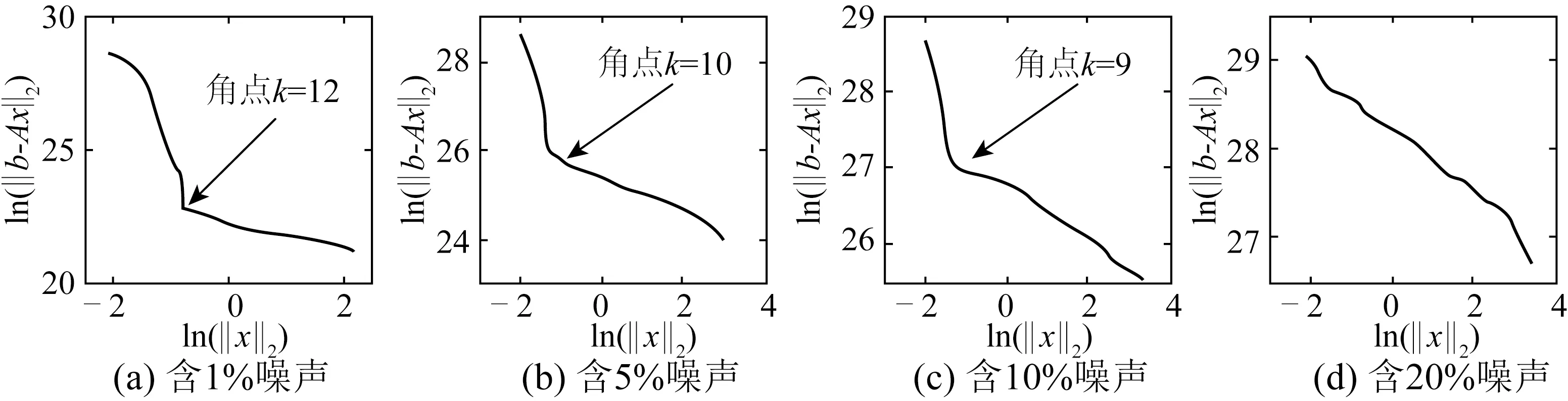
圖7 L-曲線圖Fig.7 L-curves

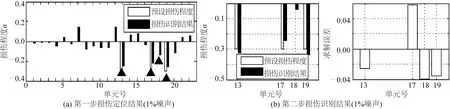
圖8 利用兩步式CMCM模型修正方法進行損傷識別 (1%噪聲)Fig.8 Damage identification with two-step CMCM model updating method (1% noise)

圖9 利用兩步式CMCM模型修正方法進行損傷識別 (5%噪聲)Fig.9 Damage identification with two-step CMCM model updating method (5% noise)

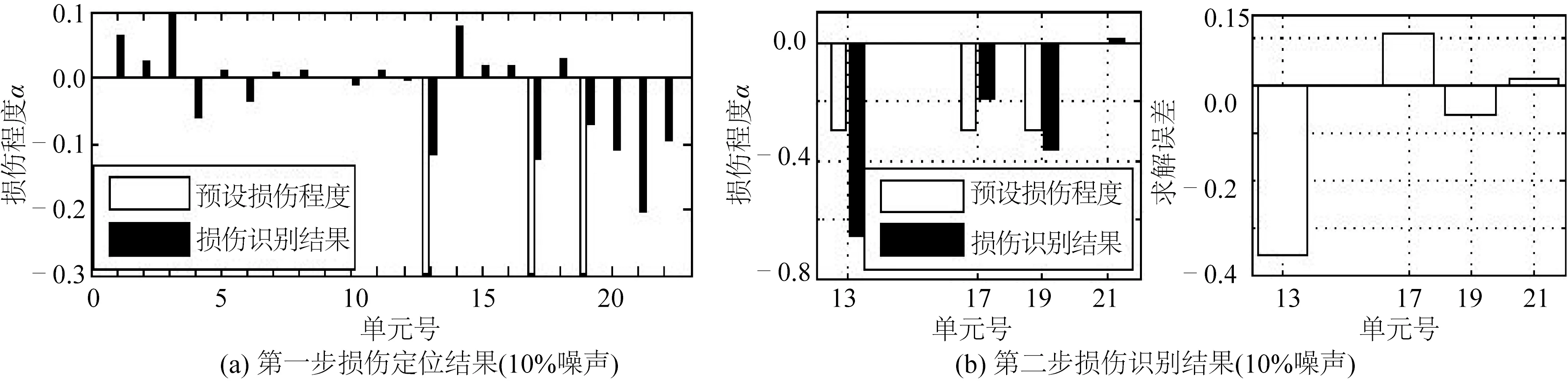
圖10 利用兩步式CMCM模型修正方法進行損傷識別 (10%噪聲)Fig.10 Damage identification with two-step CMCM model updating method (10% noise)

通過比較可以看出，隨著噪聲水平的提高，“L-曲線”逐漸趨于平滑，當噪聲水平達到20%時，很難選定截斷數k。但對于能夠通過“L-曲線”選定出截斷數的三個噪聲工況，均可以在第一步模型修正中通過TSVD求解方法定位損傷位置，在第二步模型修正中確定損傷程度。但隨著噪聲水平的提高，損傷程度識別誤差不斷增大，造成這一結果的主要原因是，隨著噪聲水平的提高，模型修正方程組的病態性不斷增大，為防止解的“震蕩”，利用L曲線選取的截斷數不斷變小，這使得解趨向于最小范數解，而偏離最小二乘解，從而造成誤差的增大。

為體現以上兩步式模型修正方法的優越性，采用模態應變能法分別對四種噪聲水平工況進行了對比研究，結果如圖11所示。可以看出，當噪聲水平為0.5%時，模態應變能指標可以準確的定位單元13、17和19的損傷，損傷程度均在-0.3附近，與預設值吻合較好；當噪聲水平提高到1%時，損傷程度識別誤差增大，且明顯高于圖8所示兩步式模型修正方法給出的誤差值；當噪聲水平增大到5%和10%時，僅能定位到單元17的損傷，且損傷程度識別誤差較大。由此可見，兩步式模型修正方法比模態應變能法具有更強的噪聲魯棒性。除此之外，模態應變能指標還造成了單元4、5和6的損傷誤判，而兩步式模型修正方法通過第一步初步定位可以有效地避免這一問題。

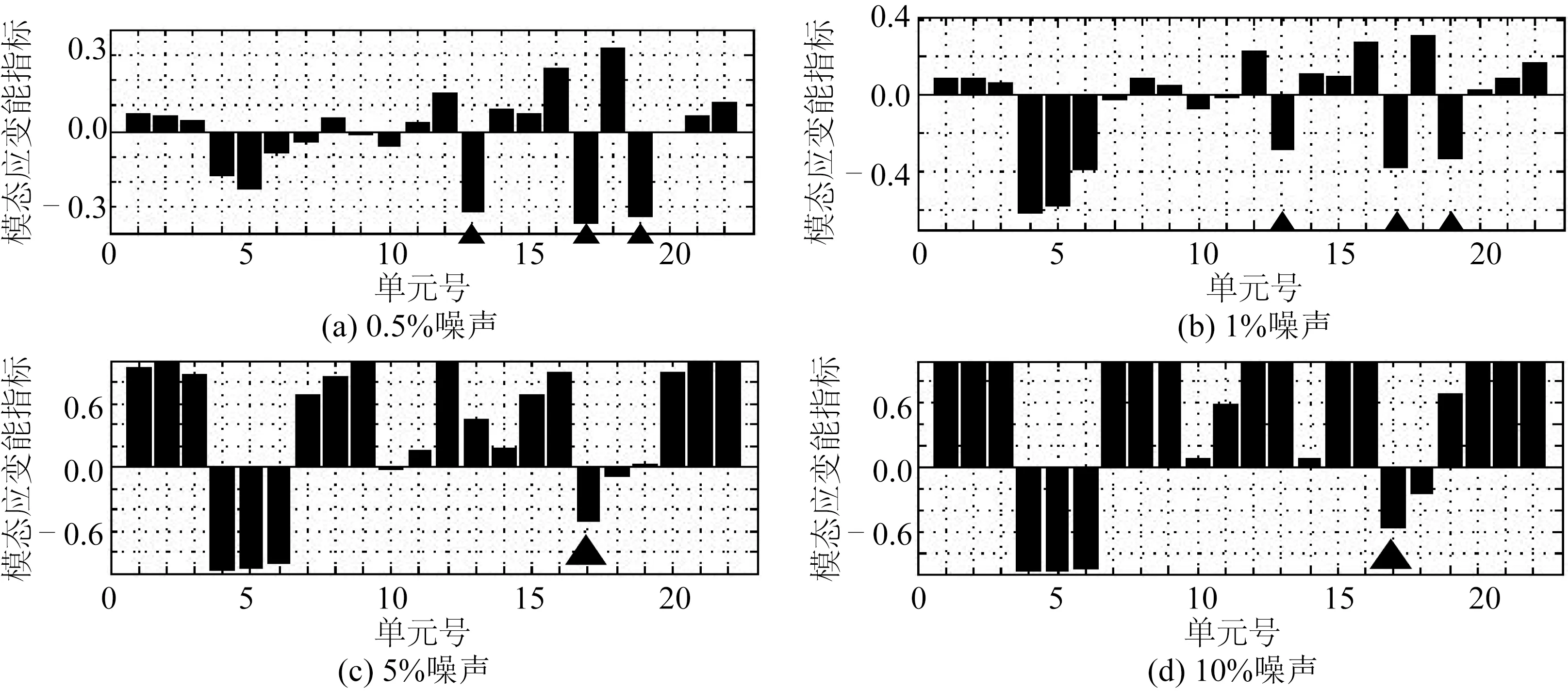
圖11 利用模態應變能法識別各噪聲水平工況下的損傷Fig.11 Damage identification of different noise levels with modal strain energy method

3.3.3 工況3：振型空間不完備且包含噪聲

假定實際測試中，只在結點11～17的三個平動自由度(x、y和z)上布置傳感器，即通過測試僅獲得21個自由度的振型值。且假定實測模態振型中包含1%的噪聲。采用2.3中Guyan方法對實測振型進行擴階。

第一步：先將全部22個單元作為損傷識別對象，利用前6階實測模態和前6階有限元模態，構建36個CMCM方程。利用“L-曲線”選取截斷數k=8，如圖12(a)所示。采用TSVD 方法求取正則解，根據這一結果可初步定位損傷位置為單元13、單元17、單元18和單元19，如圖12(b)所示。

第二步：將初步定位的四個損傷單元作為識別對象，利用第3～6階實測模態和第3～6階有限元模態，重新構建Nm=16個CMCM方程，此時Ne=4。采用奇異值分解法(SVD)進行求解，結果如圖12(c)所示，經過第二次識別，可以相對準確地定位出損傷位置和損傷程度。與圖8所示振型空間完備工況相比，損傷識別誤差稍大。由此可見，當實測模態振型空間不完備時，擴階過程也會造成一定的識別誤差，但影響不大。

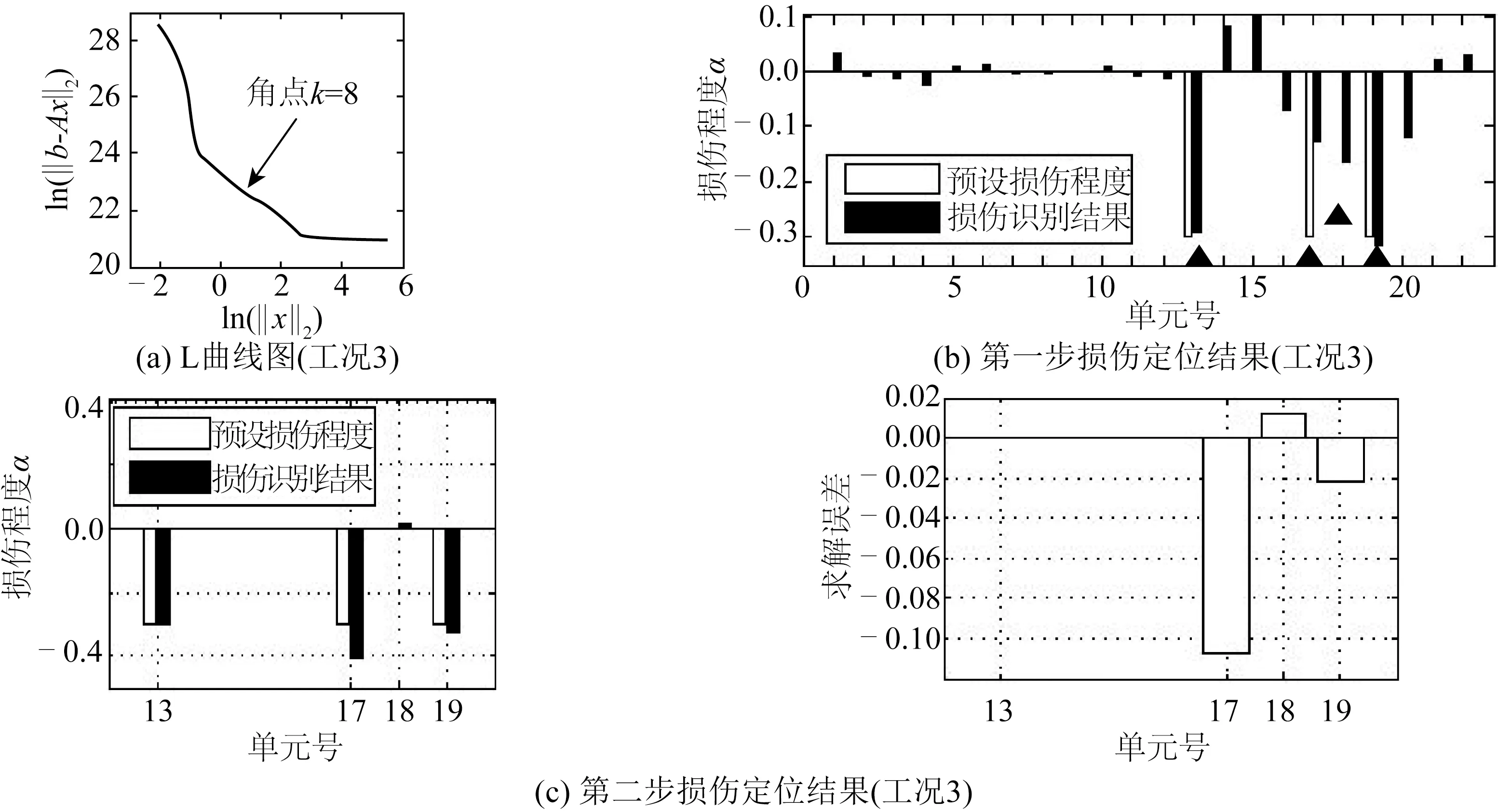
圖12 利用兩步式CMCM模型修正方法識別工況3損傷Fig.12 Damage identification of Case 3 with two-step CMCM model updating method

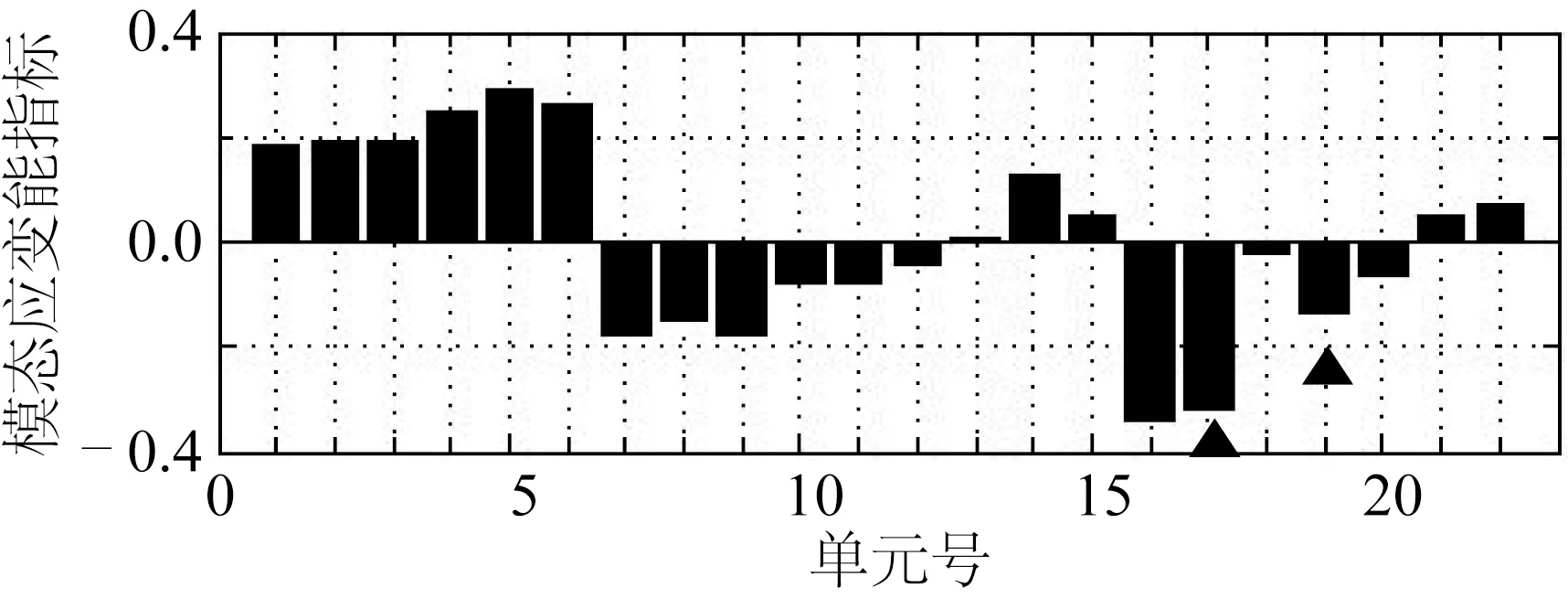
圖13 利用模態應變能法識別工況3損傷Fig.13 Damage identification of Case 3 with modal strain energy method

同樣采用模態應變能法進行對比研究，結果如圖13所示。該方法僅能定位到單元17和單元19的損傷，且損傷程度識別結果誤差較大；另外，還造成了水平撐單元7～9和單元16等更多單元的損傷誤判。與圖11(b)所示振型空間完備工況對比可見，模態擴階過程對模態應變能方法的損傷識別結果影響較大。

4 結 語

1)將一種新提出的交叉模型交叉模態模型修正方法(CMCM)應用到了海上風電支撐結構的損傷識別中。并提出了一種兩步式模型修正過程：第一步，將結構的所有單元作為對象，利用CMCM方法進行傷識別，根據結果對損傷位置進行初步定位；第二步，將初步定位損傷的單元重新選作損傷識別對象，再次利用CMCM方法實現對損傷位置和損傷程度的精確識別。數值算例表明，該方法與模態應變能法相比具有較強的噪聲魯棒性和振型擴階容差性，且能有效的避免損傷的誤判。

2)當用CMCM方法構建的損傷識別方程組呈現一定程度的“病態”時，在測量噪聲的影響下，最小二乘解容易導致求解失效。采用TSVD正則化方法進行求解可有效解決這一問題。

3)在測量模態不完備且含有一定噪聲的情況下，結合傳統的Guyan擴階技術，采用兩步式模型修正過程可以較好地識別海上風電支撐結構的損傷。

[1] LIU F,LI H,LI W,et al.Experimental study of improved modal strain energy method for damage localization in jacket-type offshore wind turbines [J].Renewable Energy,2014,72:174-181.

[2] SOHN H,FARRAR C R,HEMEZ F M.A review of structural health monitoring literature:1996-2001[R].Los Alamos National Laboratory Rep.No.LA-13976-MS,2003.

[3] PEETERS B,MAECK J,ROECK G D.Vibration-based damage detection in civil engineering:excitation sources and temperature effects [J].Journal of Smart Materials and Structures,2001,10(3):518-527.

[4] HU S J,LI H J,Wang S Q.Cross-model cross-mode method for model updating [J].Mechanical Systems and Signal Processing,2007,21(4):1690-1703.

[5] LI H J,WANG J R,HU S J.Using incomplete modal data for damage detection in offshore jacket structures [J].Ocean Engineering,2008,35(17-18):1793-1799.

[6] 李英超.基于模態參數識別的海洋平臺結構模型修正技術研究[D].青島：中國海洋大學，2012.(LI Yingchao.Study on finite element model updating for offshore platform structures based on vibration test [D].Qingdao:Ocean University of China,2012.(in Chinese))

[7] TIKHONOV A N.Solution of incorrectly formulated problems and the regularization method [J].Soviet Math,Dokl,1963,4：1035-1038.

[8] MARES C,FRISWELL M I.MOTTERSHEAD J E.Model updating using robust estimation [J].Mechanical Systems and Signal Processing,2002,16(1)：169-183.

[9] FRISWELL M I,MOTTERSHEAD J,AHMADIAN H.Finite-element model updating using experimental test data:parameterization and regu1arization[J].Philosophical Transactions of the Royal Society of London,2001,359：169-186.

[10] CALVETTI D,REICHEL L,SGALLARI F,et al.A regularizing lanczos iteration method for underdetermined linear systems [J].Journal of Computational and Applied Mathematics,2000,115：101-120.

[11] 吳頡爾.正則化方法及其在模型修正中的應用[D].南京：南京航空航天大學,2007.(WU Jieer.The regularization method with application to finite element model updating [D].Nanjing:Nanjing University of Aeronautics and Astronautics,2007.(in Chinese))

[12] 肖庭延,于慎根,王彥飛.反問題的數值解法[M].北京：科學出版社,2003.( XIAO Tingyan,YU Shengen,WANG Yanfei.Numerical solution of inverse problem [M].Beijing:Science Press,2003.(in Chinese))

[13] KIM J T,STUBBS N.Improved damage identification method based on modal information[J].Journal of Sound and Vibration,2002,252(2):223-238.

[14] ZAAIJER M B.Foundation modeling to assess dynamic behaviour of 0ffshore wind turbines[J].Applied Ocean Research,2006,28,45-57.

[15] JAN V T.Design of supports for offshore wind turbines [D].Delft:Delft University of Technology,2006.

[16] WANG S Q.Damage detection in offshore platform structures from limited modal data [J].Applied Ocean Research,2013,41:48-56.

Damage identification of offshore wind turbine support structure with a two-step model updating process

LI Yingchao1,ZHANG Min2,WANG Shuqing2

(1.College of Civil Engineering,Ludong University,Yantai 264025,China; 2.College of Engineering,Ocean University of China,Qingdao 266100,China)

P752; P741

A

10.16483/j.issn.1005-9865.2016.03.004

1005-9865(2016)03-0028-10

20105-06-09

國家自然科學基金項目(51379196，51209189)；山東省自然科學基金項目(ZR2013EEQ006)；泰山學者工程專項經費；魯東大學科研基金項目(LY2013027)

李英超(1985-)，女，山東煙臺人，博士，講師，主要從事海洋工程結構健康監測研究。E-mail：yingchao.ouc@163.com