計及系統穩定性和電磁特性的電動機聚合方法

戴麗麗，黃小慶，曹一家，張志丹，許雅婧

（湖南大學電氣工程學院，長沙　410082）

各電動機轉子側的輸出功率Poi、轉子銅耗Pri分別為

計及系統穩定性和電磁特性的電動機聚合方法

戴麗麗，黃小慶，曹一家，張志丹，許雅婧

（湖南大學電氣工程學院，長沙410082）

針對傳統電動機聚合方法沒有考慮電動機轉子電磁暫態特性的不足，該文提出了一種計及系統穩定性和電磁特性的電動機聚合方法。首先，分析影響電力系統穩定性的主要電動機參數，并以這些參數組成特征向量，將電動機群分為系統穩定性好和穩定性差的兩組；其次，根據各電動機的實際運行工況，綜合考慮電動機轉子電磁、機械特性，求解聚合電動機的運行滑差，進而求解聚合電動機的電氣參數；最后搭建IEEE9節點系統對該方法進行仿真驗證。結果表明，相對于傳統容量加權法以及同調動態聚合方法，將原電動機群聚合成單臺電動機時，文中方法聚合精度最高，且計算量比同調動態聚合法小；同時，通過聚類采用兩臺等值電動機模擬原電動群，比單臺等值電動機的誤差更小，其動態響應曲線幾乎與原電動機群吻合。

電動機聚合；系統穩定性；運行工況；電磁特性；機械特性

感應電動機是電力負荷（特別是工業負荷）中最重要的動態成分，其模型參數對電力系統仿真精度，尤其是對暫態穩定仿真精度[1]，有著重要的影響。鑒于電動機數量龐大、類型眾多、地點分散的特點，且受計算機存儲容量、計算時間的限制，在實際的仿真過程中，既無必要也不可能對供、配電網絡上的所有電動機進行一一建模，通常用單臺或兩臺等值電動機模擬一群電動機的負荷特性[2]。

電動機的聚合在滿足一定精確度的同時，追求算法簡單，計算量小，但這兩者之間往往存在矛盾。迄今為止，國內外對電動機的聚合進行了大量的探討研究。文獻[3]通過電動機參數修正電動機的加權因子，進而求解聚合電動機的參數。文獻[4]假設電動機堵轉，對電動機的穩態等值電路等效轉換后進行聚合。文獻[5]基于電動機空載和堵轉兩種特殊工況下的聚合。

以上方法都未考慮電動機的電磁暫態特性。文獻[6]指出對于大型的電動機，q軸暫態電勢是電動機動態特性的主導因素。因此，為提高聚合的精確度，對電動機進行聚合時有必要考慮電動機的電磁暫態特性。文獻[7]基于同調性對電動機的機電暫態模型進行動態聚合，為簡便稱呼，下文中的同調動態聚合皆指該方法。同調動態聚合法提高了一定的精確度，但該算法復雜，計算量大，且其聚合精確度受參數初始值的影響較大。

當電動機特性差異較大時，為更精確地模擬原電動機群，可先對電動機群進行分組，再分別對每一組電動機進行聚合。電動機的動態特性與其參數密切相關，當電動機參數不同時，其系統穩定性也不一樣。同時，電動機各參數對系統穩定性的影響大小也各不相同[8]。

基于以上分析，本文提出一種計及系統穩定性和電磁特性的電動機聚合方法。該方法不但提高了聚合精確度，而且參數聚合的程序簡單，計算量小。

1　三階暫態感應電動機模型

1.1感應電動機的等值電路

感應電動機三階機電暫態模型的等值電路如圖1所示。

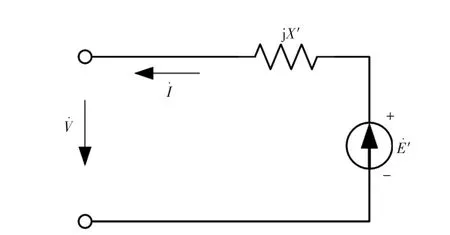
圖1　感應電動機三階暫態等值電路Fig.1　Transient equivalent circuit of induction motor

感應電動機的定子電阻一般很小，可忽略不計，即定子電阻R1=0。感應電動機的三階機電暫態的微分方程為

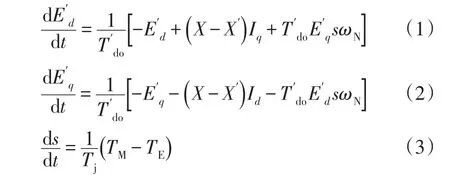
式中：E'd、E'q分別為轉子暫態電勢的d、q軸分量；X=X1+Xu，X'=X1+X2Xu（/X2+Xu），X1、X2、Xu分別為定子電抗、轉子電抗、勵磁電抗；s為運行滑差；Tj、T′do分別為轉子慣性時間常數和定子暫態開路時間常數；ωN為同步角速度。以上所有的參數皆是以電動機自身的容量基準下的標幺值。式（1）～（2）是轉子回路電磁暫態過程的微分方程。式（3）為轉子機械暫態過程的微分方程。

1.2感應電動機的初始求解

在已知各電動機的負荷大小及其電氣參數的前提下，對電動機群進行聚合。由于各電動機的參數是以其自身容量為基準值，且其容量基準可能存在差異。因此，在聚合之前，應先統一電動機的基準。在此基礎上，對電動機進行初始化，求解各電動機的初始滑差s，暫態電勢E'，為后續的電動機聚合奠定基礎。

1）基準轉換系數K的求解

電動機阻抗由本身基準下的標幺值轉換到系統基準下的標幺值的轉換系數K為

式中：SN為電動機額定容量；SB為系統基準容量。

2）初始滑差s的求解

初始滑差s可通過電動機的負載率求解得到。感應電動機的負載率LFM為電動機實際吸收的功率與其額定容量的比值[9]，即

P=LFMPN（5）式中：P為電動機實際吸收功率；PN為電動機的額定有功功率。

忽略定子電阻，電動機實際吸收功率為

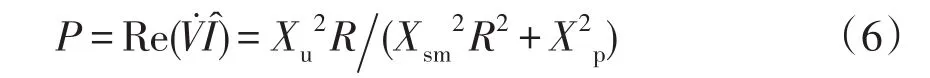
式中：R=R2s，其中R2為電動機的轉子電阻；Xsm=X1+Xu，Xp=X1X2+X1Xu+X2Xu。

結合式（5）和式（6）從而可直接通過電動機的負載率求解出各電動機的初始運行滑差s。

3）暫態電勢E'的求解

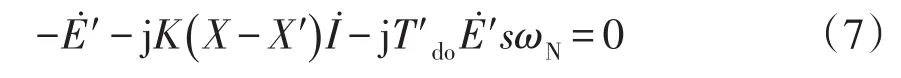
由電路圖1可知電動機定子側電流為

則可求出各電動機的暫態電勢E?′為

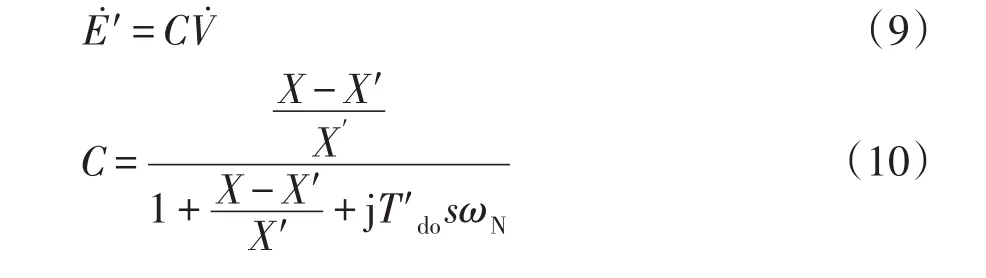
2　感應電動機聚合

2.1聚合電動機初始滑差的計算

假設n臺電動機連接在同一母線下，如圖2所示。經轉換系數Ki，各電動機的阻抗為統一基準下的標幺值，基于戴維南等效定理，聚合電動機的等效阻抗Zeq、等效電源E′eq分別表示為

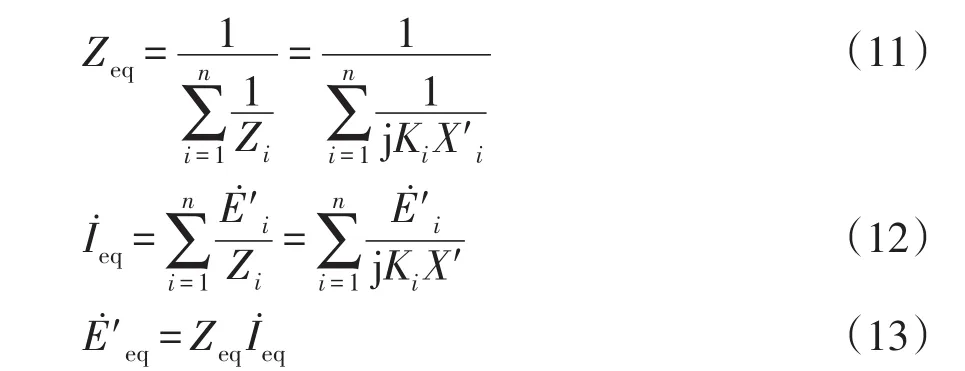
各電動機轉子側的輸出功率Poi、轉子銅耗Pri分別為

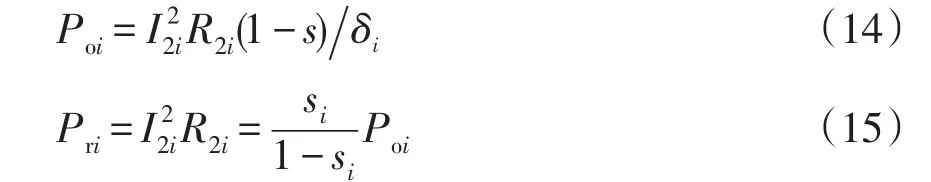
從電動機的等值電路可看出，各電動機轉子側的輸出功率Poi為

從而可得到各電動機轉子側消耗的銅耗Pri為

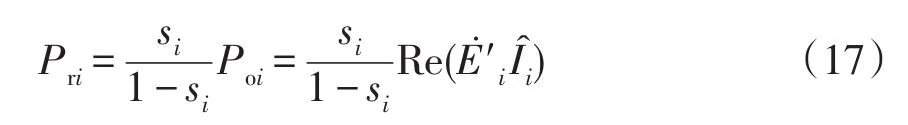
根據聚合前后電動機消耗的轉子銅耗相等，則有

式中，Preq為聚合電動機轉子銅耗。

在第1.2節求得各電動機的初始滑差s，暫態電勢E′的基礎上，通過式（18）則可得到聚合電動機的初始滑差seq。通過綜合考慮電動機的機電暫態特性，即轉子機械特性和轉子電磁暫態特性，求解聚合電動機的初始滑差，將有利于提高聚合的精確度。

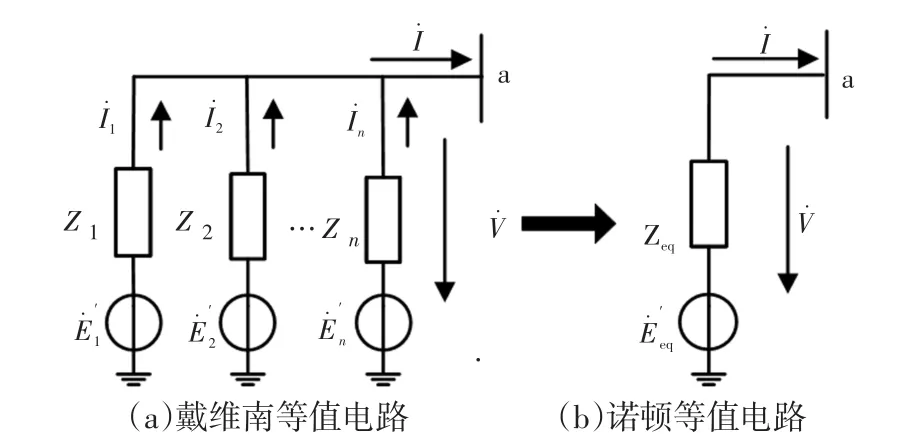
圖2　同一母線下n臺電動機暫態等值電路Fig.2　Transient equivalent circuit of n induction motors on the same bus

2.2聚合電動機電氣參數的計算

圖2（b）的諾頓等值電路如圖3所示，則聚合電動機的等效阻抗可進一步表示為

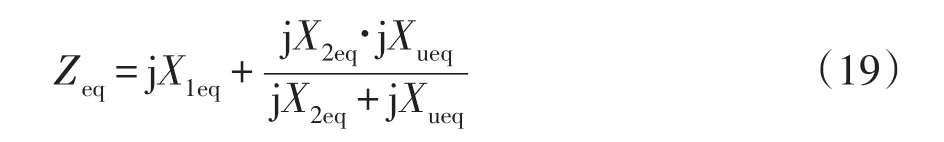
式中，X1eq、X2eq、Xueq分別表示聚合電動機的定子電抗、轉子電抗、勵磁電抗，且有

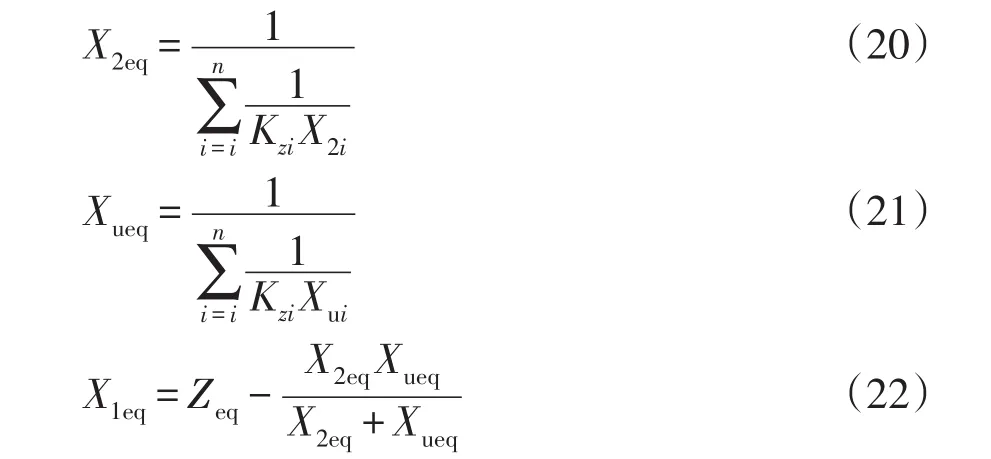
式中：Pi為各電動機從電網吸收的有功功率；SiN為各電動機的額定容量。根據式（6）則可求出聚合電動機的轉子電阻R2eq，則聚合電動機的所有電氣參數都求解出來。

聚合電動機的負載率LFMeq為

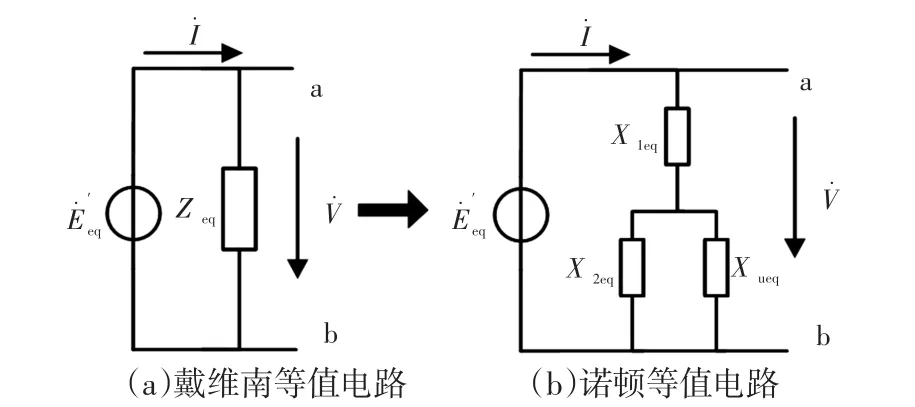
圖3　聚合電動機的諾頓等值電路Fig.3　Norton equivalent circuit of the aggregate induction motor

2.3聚合電動機慣性時間常數的計算

假設聚合前后電動機轉子的動能相等，有

式中：SiN為各電動機的額定容量；Hi為各電動機的慣性常數；Sagg為聚合電動機的額定容量。根據式（24）和式（25）可求出聚合電動機的慣性常數Hagg。

我國通常習慣用慣性時間常數，慣性常數與它有兩倍的關系，即Tj=2H。

3　感應電動機聚類分組

電動機參數不同，其系統穩定性也不相同，且各參數對系統穩定性的影響大小也各不相同。本文通過篩選對系統穩定性影響較大的幾個關鍵電動機參數作為特征向量，對電動機進行聚類，分成系統穩定性好和穩定性差的兩組。通過關鍵參數的選取，既可以反映該系統的穩定性，從而保證聚類的有效性，也可減少計算量。

3.1特征值的選擇

聚類效果的好壞與特征值的選取有密切的關系，特征值選取的不當會造成分類無效[10]。大量文獻研究[11-12]表明：電動機參數對電力系統穩定性的影響大小依次為初始滑差、轉子電阻、定子電抗和轉子電抗，且轉子電阻越大，系統越穩定，而定子電抗、轉子電抗越大，穩定性越差。據此得出電動機的臨界滑差scr為

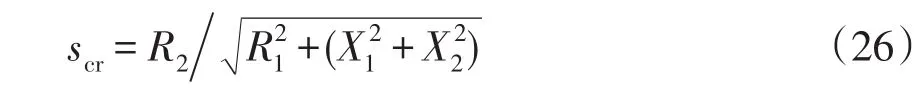
能綜合反映出轉子電阻、定子電抗、轉子電抗等電氣參數對系統穩定性的影響，且對系統穩定性的影響較大。由此可知，初始滑差和臨界滑差對系統的穩定性影響較大，通過這兩者可以整體地反映系統的穩定性。同時，文獻[13]指出初始滑差s和臨界滑差scr對電動機的聚合結果具有較大的影響。

基于以上分析，本文選用初始滑差和臨界滑差作為電動機聚類的特征向量，從而將系統穩定性好的電動機聚類為一組，系統穩定性差的電動機聚為一組。

3.2聚類算例

為了驗證該方法的有效性，本文采用文獻[3]中的6臺電動機進行驗證，6臺電動機的輸入特征向量如表1所示，通過譜系數聚類[14]后的結果如圖4所示。由圖4可知，前4臺電動機歸為一組，后兩臺電動機歸為一組，與文獻[3]中改進型的分組結果相一致，從而驗證該方法的有效性。文獻[15]的研究表明大型電動機有利于系統穩定，相比于電動機1～4的民用電器，電動機5、6為工業電動機，屬于大型電動機。且由表1可看出，電動機5、6的初始滑差較低，臨界滑差較高，該系統穩定性較高，與文獻[15]的結論相一致，進一步證明該分組的合理性。

表1　6臺感應電動機的特征向量Tab.1　Eigenvector of 6 induction motors

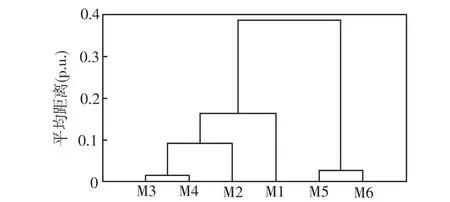
圖4　6臺電動機分類結果Fig.4　Classification results for 6 induction motors

4　算例分析

4.1仿真場景

以IEEE9節點系統為例，母線A，母線C和母線2接恒阻抗負荷，在母線B處連接一臺變壓器帶一110 kV母線，多臺不同類型的電動機直接接在110 kV的母線上，如圖5所示。其中，母線A上輸出有功功率PA=1.25 p.u.、無功功率QA=0.7 p.u.；母線C上輸出有功功率PC=1 p.u.、無功功率QC= 0.55 p.u.；母線2上輸出有功功率P2=0.35 p.u.、無功功率Q2=0.01 p.u.；母線BM上輸出的有功功率功率PBM=0.696 p.u.、無功功率QBM=0.56 p.u.。

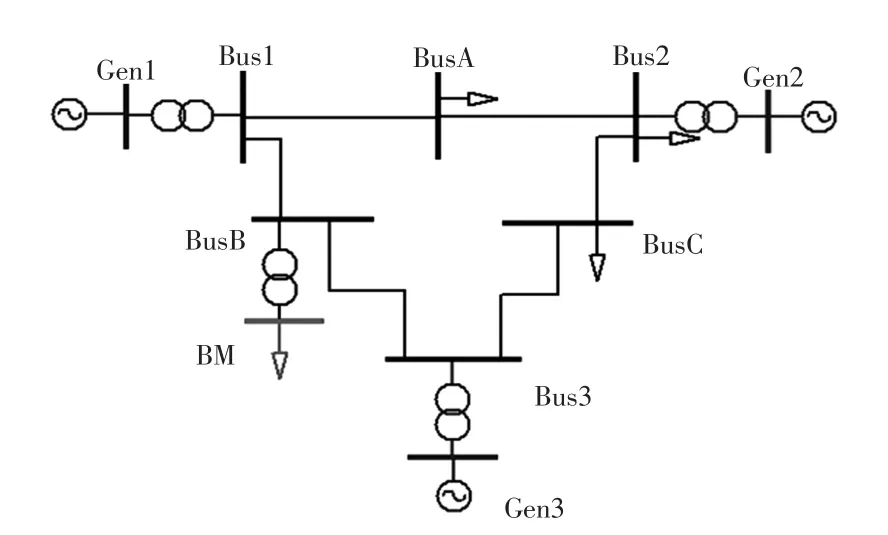
圖5　IEEE9節點系統Fig.5　IEEE9 power system

4.2電動機分類及其聚合結果

本文選取12臺IEEE典型電動機參數[16]，這12臺電動機的差異較大，如表2所示。為方便比較本文聚合方法與容量加權法、同調動態聚合法的精度，分別采用這3種方法將這12臺電動機聚合成單臺電動機，聚合后的電動機參數如表3中M1、M2、M3所示。其中，M1為采用容量加權法獲得的單臺等值電動機，M2為采用同調動態聚合方法獲得的單臺等值電動機，M3為采用本文的聚合方法獲得的單臺等值電動機。

以初始滑差和臨界滑差作為電動機聚類的特征向量，經過譜系數聚類后的結果如圖6所示。根據譜系數聚類原理[14]，類與類之間的距離越小，相似度越大。由圖6可以看出電動機5、6、11、12的平均距離較小，電動機特性相似度較大。因此，可將這4臺聚為第1組，剩下8臺電動機聚為第2組。分組后，采用本文的聚合方法對這兩組電動機進行聚合，聚合后的電動機參數如表3中M31和M32所示，其中M31為4臺電動機聚合成一臺電動機的參數，M32是剩下8臺聚合成一臺電動機的參數。

表2　12臺IEEE典型電動機模型參數Tab.2　Parameters of 12 IEEE typical induction motors p.u.

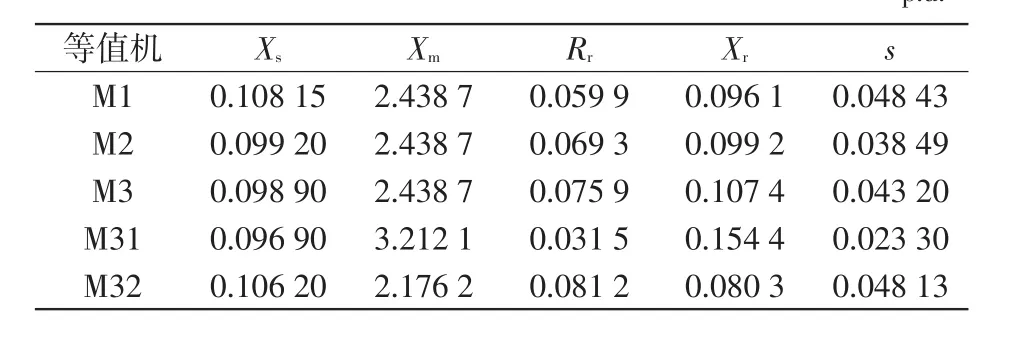
表3　聚合電動機的參數Tab.3　Parameters of the aggregate induction motors

圖6　12臺電動機分組結果Fig.6　Classification results for 12 induction motors

4.3暫態仿真結果與分析

故障設置：0.2 s在線路bus3-busC接近母線3處發生三相短路，0.3 s切除故障。采用PSASP 6.28軟件進行仿真。與原始系統相比，幾種方法仿真結果的有功功率、無功功率、母線電壓、發電機功角及角速度的相對誤差如表4所示。限于篇幅，本文只取母線電壓、發電機功角、及角速度的仿真圖做比較分析，如圖7和圖8所示。其中，原始曲線是指12臺電動機的仿真曲線；容量單臺是指采用容量加權法的單臺等值電動機的仿真曲線；同調單臺是指采用同調動態聚合法的單臺等值電動機的仿真曲線；本文單臺是指采用本文聚合方法的單臺等值電動機的仿真曲線；本文兩臺是指采用本文方法的兩臺等值電動機的仿真曲線。

表4　幾種方法的誤差比較Tab.4　Comparison of fitting error among four methods

由圖7和表4的結果可看出，分別采用容量加權法、同調動態聚合法，本文方法將這12臺電動機聚合成單臺等值電動機，本文方法的聚合精度最高，尤其在發電機功角曲線上，提高較大精度，分別由容量加權法的0.161 5和同調動態聚合法的0.144 3降到0.115 8。與同調聚合法相比，本文方法不但提高了聚合精度，同時參數聚合程序簡單，節省了計算時間。

為驗證本文電動機分組的有效性，圖8給出了采用本文聚合方法下的單臺等值電動機和兩臺等值電動機的仿真曲線對比。結果表明，以初始滑差和臨界滑差作為特征向量，采用譜系數聚類對電動機群進行分組后，采用兩臺等值的電動機模擬原電動機群，與單臺等值電動機相比較，精確度具有顯著的提高，發電機功角的相對誤差由單臺的0.115 8降到0.030 5。

此外，由表3中的M1、M2、M3可發現，3種聚合方法下的單臺等值電動機的定子電抗，勵磁電抗，轉子電抗的聚合結果相差很小，主要區別在于初始滑差跟轉子電阻。相對電動機的其他電氣參數，電動機初始滑差、轉子電阻對暫態穩定的影響較大[11]。因此，在電動機聚合時，聚合電動機初始滑差、轉子電阻的求解對聚合結果的精確度具有重要的影響。由此可知，本文聚合方法的精確度提高的最主要因素在于對電動機的初始滑差、轉子電阻的求解。

經分析，本文提出的感應電動機聚合方法的精確度提高的具體原因如下。

（1）初始滑差的求解更符合實際運行情況。以往聚合方法是先基于特殊運行工況求解電動機的參數，進而求解聚合電動機的初始滑差。本文直接根據各電動機的實際運行工況，并綜合考慮了電動機轉子機械特性和轉子電磁特性求s，因此精度更高。

（2）聚合電動機的參數求解，其中包括轉子電阻。以往的聚合方法是基于特殊的運行工況下，如堵轉或空載，獲得聚合電動機的電氣參數。而本文是先通過求解聚合電動機的初始滑差，在此基礎上，再求解聚合電動機的各電氣參數，從而在一定程度上提高了精確度。

（3）作為同樣基于電動機機電暫態模型聚合的方法，本文方法比文獻[7]的同調動態聚合精度更高，很大程度上是由于同調動態方法的精確度受參數初始值的選擇影響較大，且對于不同的電動機群，很難按經驗確定初始值。而本文的聚合方法通過代數方程求解即可得到聚合電動機參數，無須給出初始值。

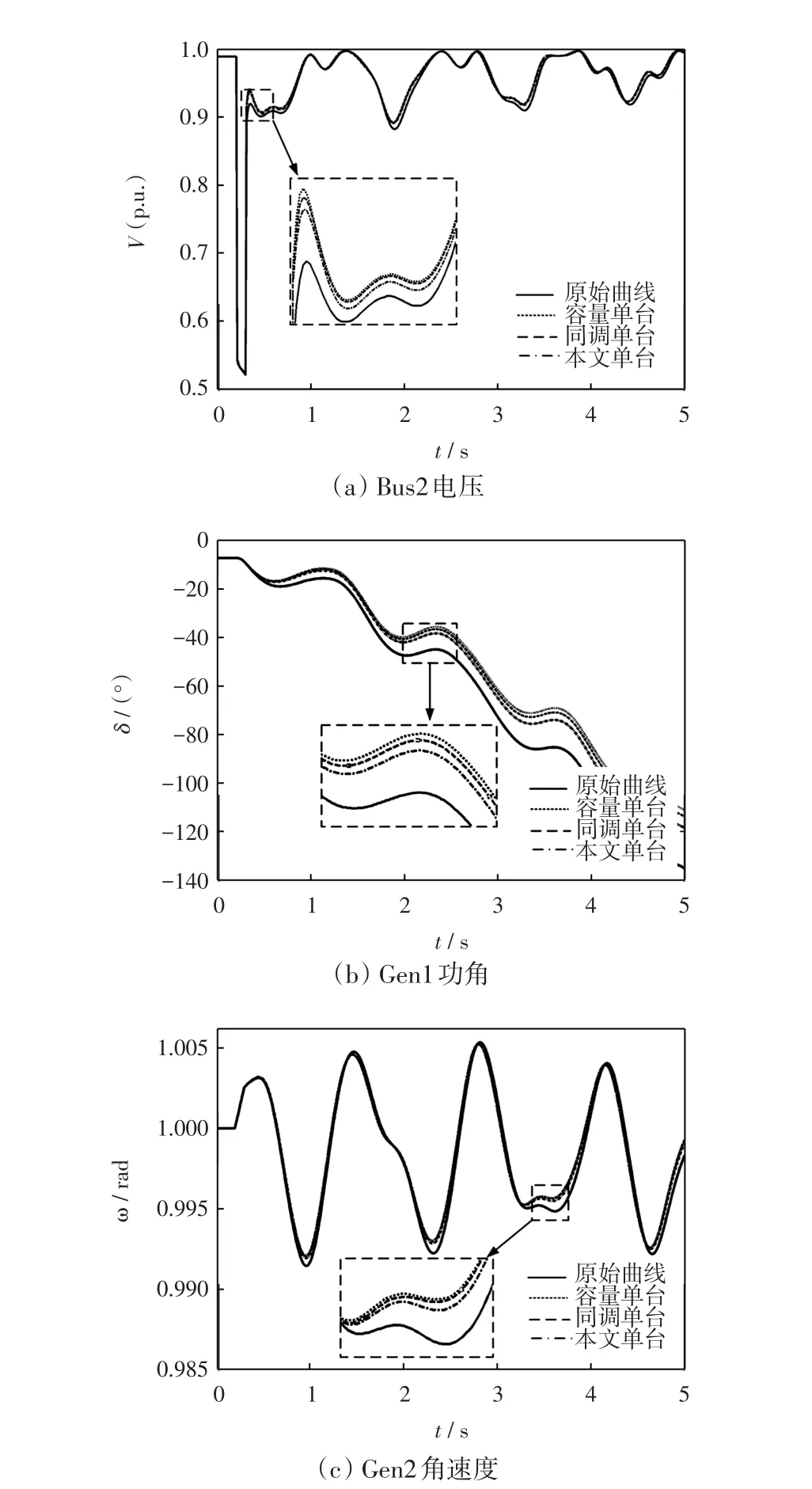
圖7　3種聚合方法的單臺等值電動機仿真曲線對比Fig.7　Simulation results comparison of one aggregate induction motor among three methods

圖8　本文聚合方法的單臺等值電動機與兩臺等值電動機的仿真結果比較Fig.8　Simulation results comparison between one aggregate induction motor and two aggregate induction

5　結語

本文提出一種計及系統穩定性和電磁特性的感應電動機聚合方法。根據系統的穩定程度，以初始滑差和臨界滑差組成特征向量，對電動機群進行分組；然后，根據電動機實際運行工況，并綜合考慮了電動機轉子電磁、機械特性，對電動機進行聚合。通過搭建IEEE9節點系統對該方法進行驗證。結果表明，與容量加權法、同調動態聚合法相比，本文方法的聚合精度較高；且與同調動態法相比，本文算法更簡單；更進一步地，相比于單機等值電動機，采用兩機等值電動機模擬原電動機群，精度顯著提高。動態響應曲線幾乎與原電動機群吻合。

實際運行中，電動機是分散在配電網各個角落，與變電站主母線的距離不等。而本文研究僅考慮同一母線上電動機的聚合，對電動機進行聚合時將造成一定的誤差。下一步將致力研究配電網對電動機聚合的影響，以提高聚合的精度。

[1]Pereira L，Kosterev D，Mackin P，et al.An interim dynam?ic induction motor model for stability studies in the WSCC[J].IEEE Trans on Power Systems，2002，17（4）：1108-1115．

[2]趙兵，湯涌，張文朝（Zhao Bing，Tang Yong，Zhang Wenchao）.感應電動機群單機等值算法研究（Study on single-unit equivalent algorithm of induction motor group）[J].中國電機工程學報（Proceedings of the CSEE），2009，29（19）：43-49．

[3]侯俊賢，湯涌，張紅斌，等（Hou Junxian，Tang Yong，Zhang Hongbin，et al）.感應電動機的綜合方法研究（Study on integration method for induction motor）[J].電網技術（Power System Technology），2007，31（4）：36-41.

[4]Franklin D C，Morelato A.Improving dynamic aggrega?tion of induction motor models[J].IEEE Trans on Power Systems，1994，9（4）：1934-1941．

[5]Louie K W，Marti J R，Dommel H W.Aggregation of in?duction motors in a power system based on some special operating conditions[C]//IEEE Canadian Conference on Electrical and Computer Engineering.Vancouver，Cana?da，2007：1429-1432．

[6]Ahmed-Zaid S，Taleb M.Structural modeling of small and large Induction machines using integral manifolds[J]. IEEETransonEnergyConversion，1991，6（3）：529-535．

[7]張劍，孫元章，徐箭，等（Zhang Jian，Sun Yuanzhang，Xu Jian，et al）.基于同調性的電動機動態聚合方法（A dy?namic aggregation method for induction motors based on their coherent characteristics）[J].電力系統自動化（Au?tomation of Electric Power Systems），2010，34（5）：48-52．

[8]孫華東，周孝信，李若梅（Sun Huadong，Zhou Xiaoxin，Li Ruomei）.感應電動機負荷參數對電力系統暫態電壓穩定性的影響（Influence of induction motor load pa?rameters on power system transient voltage stability）[J].電網技術（Power System Technology），2005，29（23）：1-6．

[9]張景超，張承學，鄢安河，等（Zhang Jingchao，Zhang Chengxue，Yan Anhe，et al）.基于自組織神經網絡和穩態模型的多臺感應電動機聚合方法（Aggregation of multi induction motors based on the self-organized neu?ral network and steady state model）[J].電力系統自動化（Automation of Electric Power Systems），2007，31（11）：44-48，86．

[10]王文生，王進，王科文（Wang Wensheng，Wan Jin，Wang Kewen）.SOM神經網絡和C-均值法在負荷分類中的應用（Application of SOM neural network and C means method in load classification）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2011，23（4）：36-39．

[11]鄭競宏，李康，朱守真（Zheng Jinghong，Li Kang，Zhu Shouzhen）.暫態穩定分析中負荷模型主導參數研究（Dominant parameters of load model in transient stabili?ty analysis）[J].電力自動化設備（Electric Power Auto?mation Equipment），2009，29（9）：1-6．

[12]趙兵，湯涌（Zhao Bing，Tang Yong）.感應電動機負荷的動態特性分析（Dynamic characteristics analysis of in?duction motor loads）[J].中國電機工程學報（Proceed?ings of the CSEE），2009，29（7）：71-77．

[13]郭金川，余貽鑫，黎鵬，等（Guo Jinchuan，Yu Yixin，Li Peng，et al）.計及負載率和臨界滑差的改進感應電動機加權聚合（An improved weighting-mean aggregation method of induction motors considering load rates and critical slips）[J].電力系統自動化（Automation of Elec?tric Power Systems），2008，32（14）：6-10．

[14]李黎（Li Li）.基于聚類分析的負荷數據分類方法的研究（The Studies on Classified Methods of Load Data Based on Clustering Techniques）[D].北京：華北電力大學電氣與電子工程學院（Beijing：School of Electrical and Electronic Engineering，North China Electric Power University），2004．

[15]Tanneeru Sirisha，Joydeep Mitra，Patil Yashwant J，et al. Effect of large induction motors on the transient stability of power systems[C]//39th North American Power Sympo?sium.Las Cruces，USA，2007：223-228．

[16]鞠平，馬大強.電力系統負荷建模[M].北京：中國電力出版社，2008．

Aggregation Method of Induction Motors Considering System Stability and Electromechanical Transient Characteristics

DAI Lili，HUANG Xiaoqing，CAO Yijia，ZHANG Zhidan，XU Yajing
（College of Electrical&Information Engineering，Hunan University，Changsha 410082，China）

As the traditional aggregation approach of induction motors does not consider the rotor’s electromagnetic characteristics，an improved method considering system stability and transient model is presented.First，by abstracting the parameters which have a crucial influence on system stability as the characteristic vectors，motors are classified into two subgroups，one subgroup with good system stability，and the other with bad system stability.Secondly，according to the operation condition of individual motor，the slip of equivalent motor is obtained based on the rotor’s electromagnet?ic and mechanical characteristics.Then electrical parameters of equivalent motor are calculated based on the slip.Final?ly，this method is verified by IEEE 9-bus system.Simulation results show that the proposed method has a higher preci?sion to simulate the original individual motors than the classical weighted method and the coherent dynamic method，and fewer calculations than the coherent dynamic method.In addition，two equivalent motors is much more accurate than one equivalent motor，the dynamic curves of two equivalent motors almost match the original motors.

induction aggregation；system ability；operational states；electromagnetic characteristics；mechanical characteristics

TM7

A

1003-8930（2016）02-0015-07

10.3969/j.issn.1003-8930.2016.02.003

戴麗麗（1989—），女，碩士研究生，研究方向為負荷建模、靈活互動智能用電技術。Email：dai_lili@foxmail.com

黃小慶（1981—），女，通信作者，博士，講師，研究方向為彈性負荷與電網的相互關系研究、微電網和電力系統自動控制技術。Email：huang_xq@126.com

曹一家（1969—），男，博士，教授，博士生導師，研究方向為電力系統穩定與控制、進化計算與計算智能和智能控制系統與決策。Email：yijiacao@zju.edu.cn

2013-12-24；

2015-05-11

國家高科技研究發展計劃（863計劃）項目（2012AA050217）；國家自然科學基金重點資助項目（51137003）；國家電網公司科技項目（2011B-11）