雜交型馬鞍網殼結構參數化設計及形狀優化

蘇亞，鹿少博，鹿曉陽*，洪寧，陳亞若，李濤

(1.山東建筑大學 工程力學研究所,山東 濟南 250101； 2．坦佩雷理工大學 建筑學院,芬蘭 坦佩雷 FI-337203；3.濟南鍋爐集團 設計一處,山東 濟南 250022)

?

雜交型馬鞍網殼結構參數化設計及形狀優化

蘇亞1，鹿少博2，鹿曉陽1*，洪寧3，陳亞若3，李濤1

(1.山東建筑大學 工程力學研究所,山東 濟南 250101； 2．坦佩雷理工大學 建筑學院,芬蘭 坦佩雷FI-337203；3.濟南鍋爐集團 設計一處,山東 濟南 250022)

雜交型網殼可以發揮各單一傳統網殼的優點，在增大跨度的同時又可獲得較高的經濟效益。文章根據雜交型馬鞍型網殼結構特點，采用APDL參數化設計語言研制了兩類六種不同雜交型馬鞍網殼參數化設計宏程序，運用ANSYS軟件對其進行受力性能分析，并對受力性能最好的凱威特—聯方(Kie-Lam)網殼進行了108種工況形狀優化設計。結果表明：在同等工況下六種雜交型馬鞍網殼中Kie-Lam最大位移為6.9mm和最不應力為25.1MPa均最小，受力最為合理；矢高f與網殼最不利應力成反比，f每增加1m最不利應力平均下降幅度最大為0.51MPa，隨Ns變化沒有統一規律；在S=60m、f=30m不變的情況下，存在一種工況Kn=8、Nx=12和Ns=8滿足結構強度、剛度和穩定性前提下，使網殼結構總耗鋼量最輕。

雜交型馬鞍網殼；參數化設計；受力性能分析；形狀優化設計

0　引言

隨著大跨度、大空間建筑的日益普及，人們已不滿足傳統、單一網殼形式的直接運用，傾向于不同結構形式的組合、發揮各自的特點，形成滿足建筑美學及合理、經濟的新型結構形式[1]，雜交型網殼應運而生(如圖1所示)。新型雜交空間結構因幾何構造簡單、力流傳遞清楚、室內建筑效果美觀而受到工程設計人員的青睞[2]，雜交型球面、柱面網殼及馬鞍型網殼已廣泛應用于展覽館，影劇場，體育館和音樂廳等場所[3-5]。

圖1　雜交型網殼建筑結構實例圖(a) 北京奧運會羽毛球館；(b) 南京科學水利研究院河湖治理研究基地；(c) 中國石油大學青島校區體育館

雜交型馬鞍網殼給人們帶來舒適感且能增大結構跨度，改善肋環、施威德勒、聯方單一網殼類型頂點應力集中及按凱威特、三向格子型網殼規律連接桿件較多的弊端，使網格單元分布均勻，獲得較高的經濟效益。文章應用APDL參數化設計語言，研制了兩類六種雜交型馬鞍網殼的參數化設計宏程序，并對它們進行了受力性能分析和基于離散變量兩級形狀優化設計[1]，其研究結論為雜交型馬鞍網殼選型優化設計和推廣應用提供依據。

1　雜交型馬鞍網殼組合條件及幾何描述

馬鞍型網殼有五種基本網格形式：肋環型(Ribbedtype)、施威德勒型(Schwedlertype)、三向格子型(three-waygrid)、凱威特型(Kiewitttype)和聯方型(Lamellatype)，不包括短程線(Geodesictype)型(基于球面正二十面體分割的思想)，實現雜交得滿足兩個條件：(1) 在過渡圈上兩種結構形式的節點數必須相同;(2) 雜交是為了實現優化結構形式的目的，即改善結構的受力也可能改變結構重量的雜交形式。凱威特每圈的節點數都是環向區域份數的整數倍和三向格子在過渡區不滿足節點數相同，肋環、施威德勒和聯方之間不滿足條件(2)，考慮到條件(2)，肋環、施威德勒、聯方只能為下層分別和凱威特、三向格子雜交。因此兩類六種雜交型馬鞍網殼模式出現。第一類為凱威特—肋環雜交型(簡記為Kie-Rib)，凱威特—施威德勒雜交型(Kie-Sch)，凱威特—聯方雜交型(Kie-Lam)；第二類為三向格子—肋環雜交型(thr-Rib)，三向格子—施威德勒雜交型(thr-Sch)，三向格子—聯方雜交型(thr-Lam)。雜交型馬鞍網殼主要幾何參數有：跨度S、矢高f、環向區域份數Kn(對應棱角數)、上部結構徑向圈數Ns和徑向節點圈數Nx(對應網格密度)。圖2以凱威特—肋環雜交型馬鞍網殼為例描述了其主要幾何參數。

2　兩類六種雜交型馬鞍網殼的參數化設計

借鑒拓展型型球面網殼、橢圓水平投影雙曲拋物面網殼和折板網殼結構參數化設計的建模思想[6-8]，研制了兩類六種雜交型馬鞍網殼的參數化設計宏程序，限于篇幅，僅以凱威特—肋環雜交型馬鞍網殼(Kie-Rib)參數化設計為例進行說明。

2.1凱威特—肋環雜交型馬鞍網殼參數化設計

在笛卡爾坐標系下給定S、f、Kn、Nx、Ns，圓形水平投影馬鞍型曲面方程由式(1)表示為

(1)

式中:S為跨度，m;f為矢高，m;x、y、z為節點坐標。

① 計算節點坐標、并定義節點編號：首先建立凱威特型節點，令頂點為1號節點，用APDL中循環語句[9]，由頂點向外依次進行節點編號，在平面上利用等分圓心角法計算出網殼第i圈節點數Kn×i，第i (1≤i≤Ns)圈第j (1≤j≤Kn×i)份上的節點編號為j+i×Kn×(i-1)/2+1，節點坐標為： x=i×(S/(2Nx))×cos(360×(j-1)/(i×Kn))，y=i×(S/(2Nx))×sin(360×(j-1)/(i×Kn))，z=2f×(x2-y2)/S2。然后建立下部結構肋環型節點，從第Ns+1圈開始建立節點，由內向外依次進行，第j+Kn×(Ns×Ns+Ns)/2+1+Ko×(i-Ns-1) (式中Ko=Ns×Kn下同，且Ns+ 1≤i≤Nx， 1≤j≤Ko)號節點坐標為：x= i×(S/(2Nx))×cos(360/Ko×(j-1))，y=i×(S/(2Nx))×sin(360/ Ko×(j-1))，z=2f×(x2-y2)/S2。

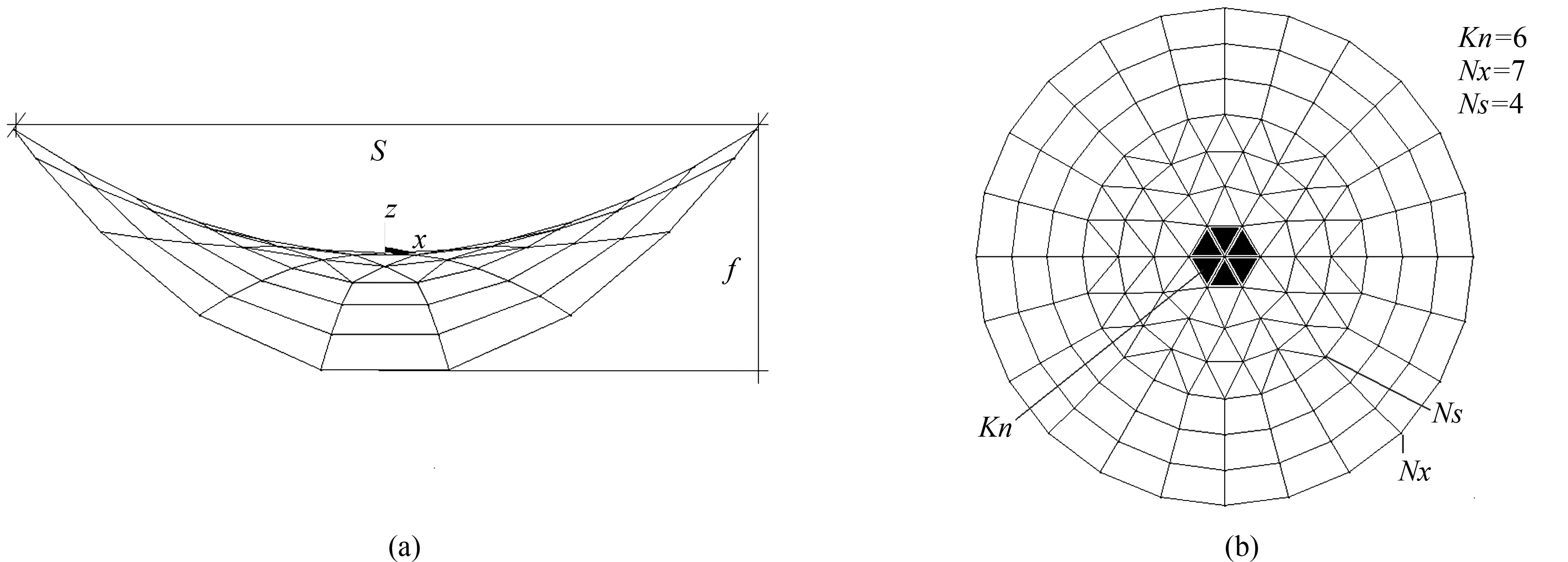
圖2　凱威特-肋環雜交型馬鞍網殼宏觀幾何參數圖(a) Kie-Rib正視圖；(b) Kie-Rib俯視圖

② 桿件連接：首先進行凱威特型桿件連接，據節點編號利用APDL循環語句按節點分布規律進行環向和徑向桿件連接。第i (1≤i≤Ns)圈第j (1≤j≤Kn×i-1)對稱區域環向桿件是連接節點j+i×Kn×(i-1)/2+1和j+i×Kn×(i-1)/2+2， 第i圈最后一對稱區域的環向桿件是由圈末節點j+i×Kn×(i-1)/2+1和首節點i×Kn×(i-1)/2+1+Kn×i連接而成。徑向桿件利用三重循環命令、按節點分布規律進行桿件連接。其次從第Ns+1圈桿件的連接方式變為肋環型，即第i(Ns+1≤i≤Nx)圈第j(1≤j≤Ko-1)對稱區域環向桿件是連接節點j+Kn×(Ns×Ns+Ns)/2+1+Ko×(i-Ns-1)和j+Kn×(Ns×Ns+Ns)/2+Ko×(i-Ns-1)+2， 第i圈最后一對稱區域的環向桿件是由節點Kn×(Ns×Ns+Ns)/2+2+Ko×(i-Ns-1)和節點Kn×(Ns×Ns+Ns)/2+1+Ko×(i-Ns-1)+Ko連接而成。徑向桿件的連接是第Ns+1圈和第Nx圈之間的徑向的節點相連，由內向外循環，第i圈第j對稱區域節點j+Kn×(Ns×Ns+Ns)/2+1+Ko×(i-Ns-1)和節點j+Kn×(Ns×Ns+Ns)/2+1+Ko×(i-Ns)相連而成。最后過渡區(即第Ns圈和第Ns+1圈之間)的桿件連接，因節點數相同，上下兩環節點相連即可。

(3) 施加約束和荷載：雜交型馬鞍網殼最外一圈節點施加固定鉸約束(限制x、y、z三個方向的線位移)，等效荷載施加在網殼所有節點上。

2.2兩類六種雜交型馬鞍網殼參數化設計實例

圖3為第一類和第二類雜交型馬鞍網殼在跨度S=60m、f=30m、Kn=6、Nx=8和Ns=5時參數化設計實例圖。

3　兩類六種雜交型馬鞍網殼受力性能分析

3.1施加約束和載荷

選取S=60m、f=30m、f/S=1/2、Kn=6、Nx=12、Ns=9兩類六種雜交型馬鞍網殼進行受力分析。桿件采用Q235鋼管，鋼材密度為7850kg/m3，彈性模量2.06×1011N/m2，泊松比0.3；桿件單元選ANSYS中BEAM4梁單元，桿件截面為Φ219×16；采用理想彈塑性材料模型，不考慮材料的強化，屈服前鋼材為線彈性，網殼最外一圈節點采用固定鉸支座(只限制x、y、z三個方向線位移，不限制轉動)，考慮結構自重，屋面施加2.35kN/m2均布荷載[10]。

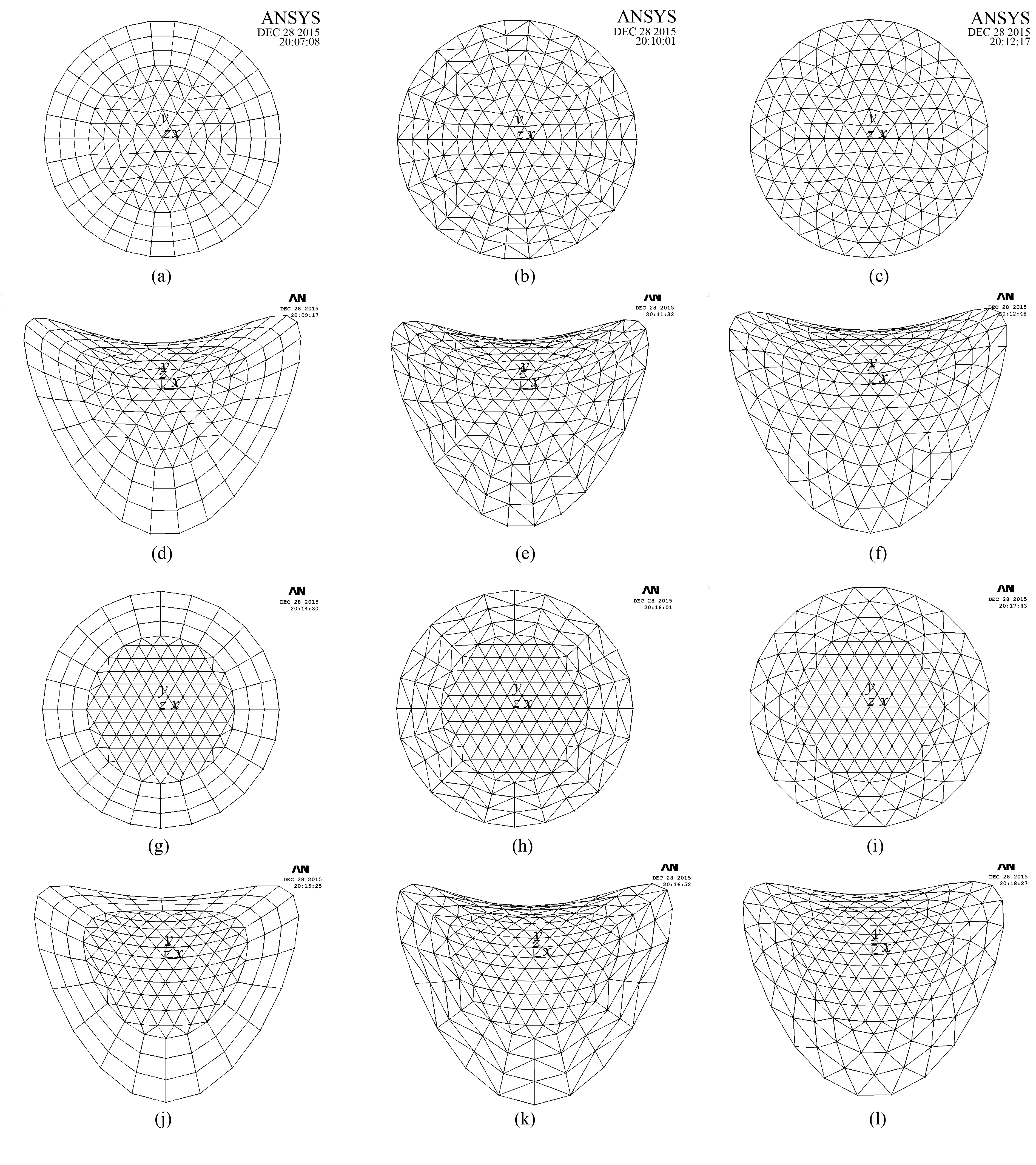
圖3　六種雜交型馬鞍網殼參數化設計圖(a) Kie-Rib俯視圖；(b) Kie-Sch俯視圖；(c) Kie-Lam俯視圖；(d) Kie-Rib軸測圖；(e) Kie-Sch軸測圖；(f) Kie-Lam軸測圖；(g) thr-Rib俯視圖；(h) thr-Sch俯視圖；(i) thr-Lam俯視圖；(j) thr-Rib軸測圖；(k) thr-Sch軸測圖；(l) thr-Lam軸測圖

3.2兩類六種雜交型馬鞍網殼受力性能分析

空間網格結構技術規程[11]中3.5.1規定，單層網殼節點最大撓度值不宜超過最短跨度的1/400，許用應力為鋼材的強度設計值215MPa。其中,S=60m，結構允許最大位移為S/400=0.15m；圖4～7分別為第一類和第二類雜交型馬鞍網殼在S=60m、f=30m、f/S=1/2、Kn=6、Nx=12和Ns=9下的位移云圖和最不利應力云圖。

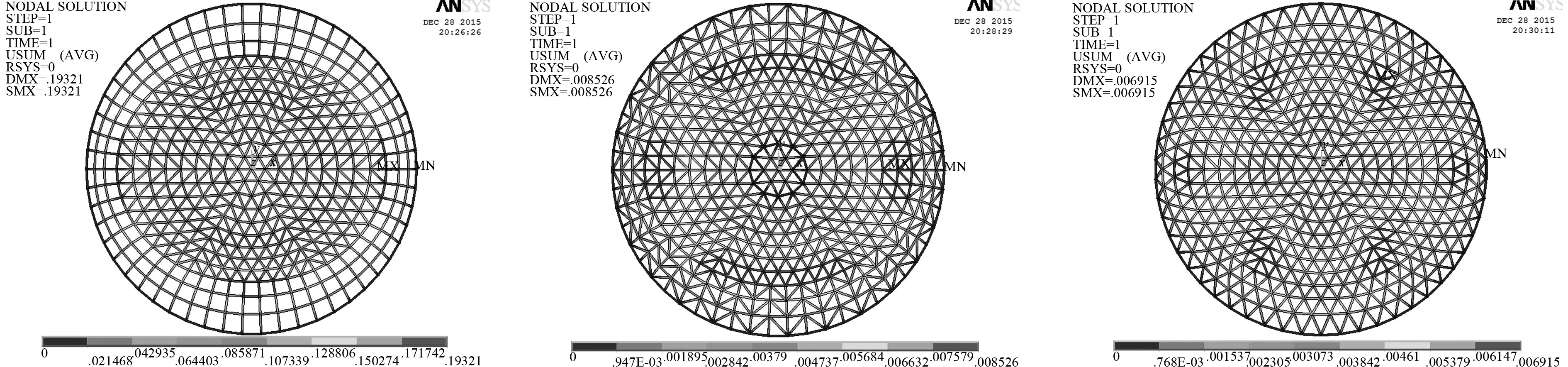
圖4　第一類雜交型馬鞍網殼位移云圖(a) Kie-Rib馬鞍網殼位移云圖；(b) Kie-Sch馬鞍網殼位移云圖；(c) Kie-Lam馬鞍網殼位移云圖

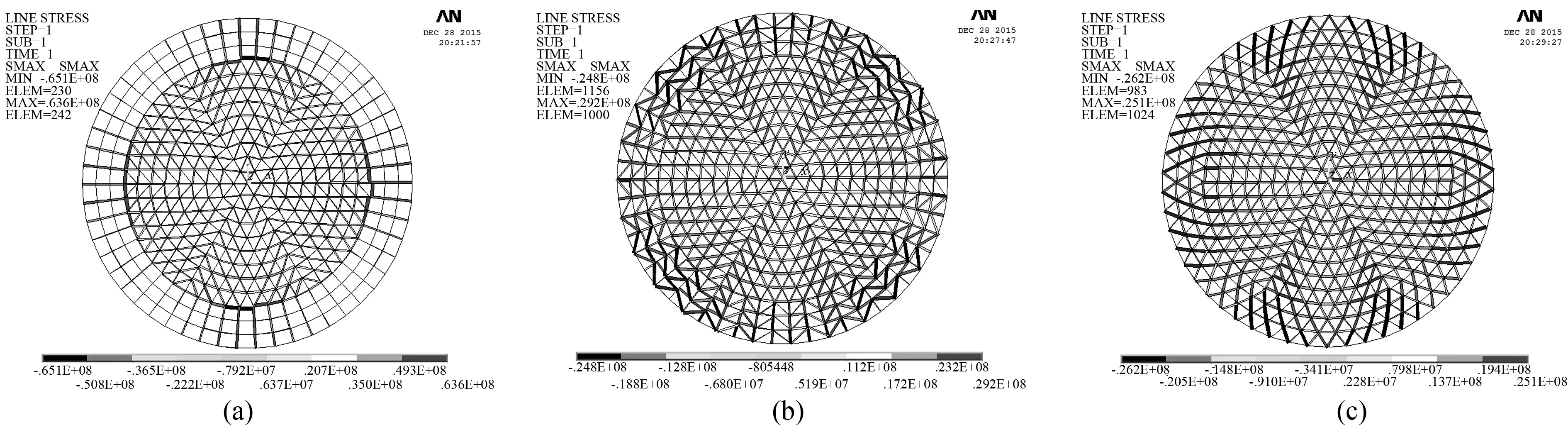
圖5　第一類雜交型馬鞍網殼最不利應力云圖(a) Kie-Rib馬鞍網殼應力云圖；(b) Kie-Sch馬鞍網殼應力云圖；(c) Kie-Lam馬鞍網殼應力云圖

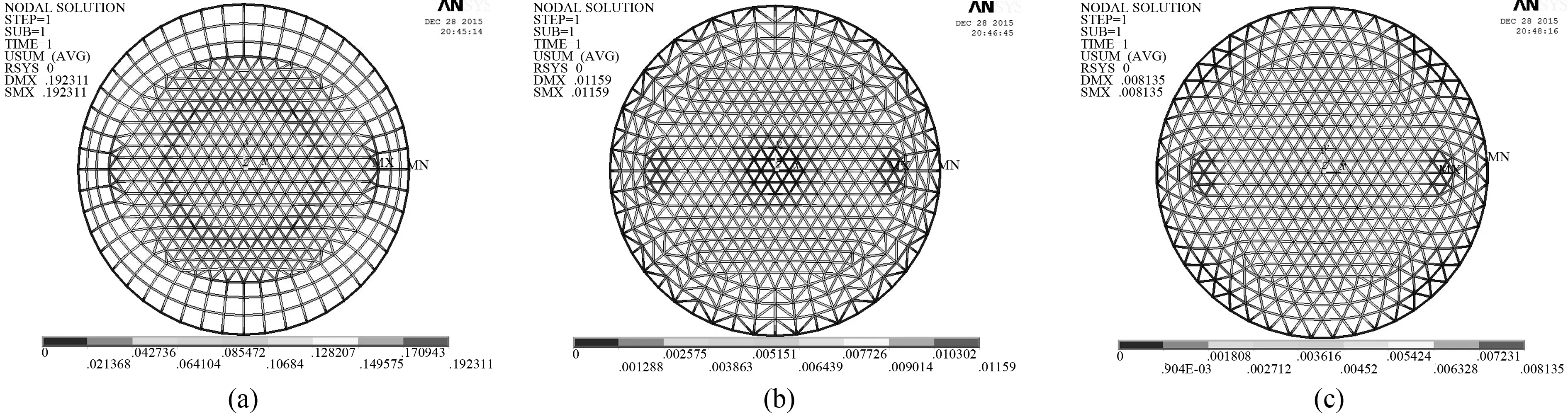
圖6　第二類雜交型馬鞍網殼位移云圖(a) thr-Rib馬鞍網殼位移云圖；(b) thr-Sch馬鞍網殼位移云圖；(c) thr-Lam馬鞍網殼位移云圖

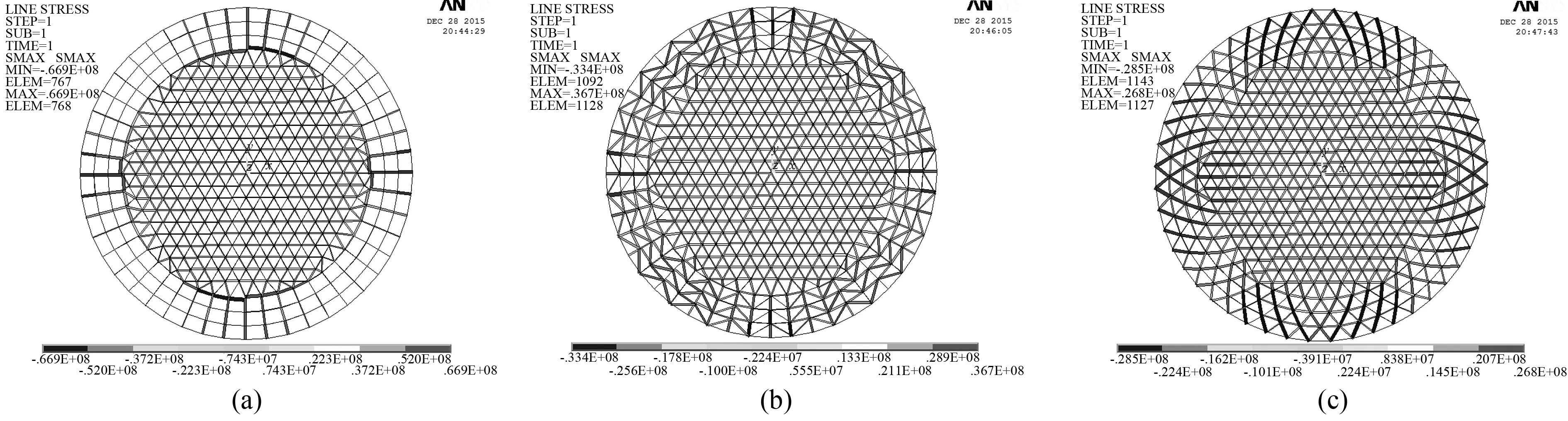
圖7　第二類雜交型馬鞍網殼最不利應力云圖(a) thr-Rib馬鞍網殼應力云圖；(b) thr-Sch馬鞍網殼應力云圖；(c) thr-Lam馬鞍網殼應力云圖

由圖4～7可知，六種雜交型網殼在豎向荷載作用下，主要由索向受拉桿件和拱向受壓桿件來承擔，中心頂點處的應力和位移均很小，成功避免了單一網殼類型頂點應力集中現象；其中，Kie-Rib和thr-Rib網殼位移和最不利應力較大區域發生在拱向和索向過渡區附近；Kie-Sch和Kie-Lam網殼位移較大的區域發生在六條主肋過渡區偏上一到兩圈，分布的區域較均勻；thr-Sch和thr-Lam網殼位移較大的區域發生在索向過渡區附近，這四種網殼最不利應力較大的區域普遍出現在拱向和索向邊緣附近，說明此處桿件強度相對較弱，設計施工時可有針對性的加強。但是，Kie-Rib和thr-Rib網殼在文中工況下最大位移分別為0.192942 和0.192001m均大于結構允許撓度0.15m，整體剛度較弱，不適合中大跨度結構，結構必須具有一定的剛度來抵抗結構的變形[12]。thr-Lam、Kie-Sch、thr-Sch的最大位移和最不利應力分別為0.008132、0.008526和0.011586m和26.5MPa、29.2MPa、36.7MPa。而Kie-Lam的最大位移0.006912m和最不利應力25.1MPa在同工況下均最小，遠小于結構允許撓度0.15m和許用應力215MPa，受力合理，可優先選用。

表1、2 給出了兩類雜交型馬鞍網殼在S=60m、f=30m、Kn=6、Nx=12和Ns=4～11時的最大位移和最不利應力值；表3、4給出了兩類雜交型馬鞍網殼在S=60m、Kn=6、Nx=12、Ns=9和f=15m～50m時的最大位移和最不利應力值。其中，最不利應力是負值，代表壓應力；正值，代表接應力。

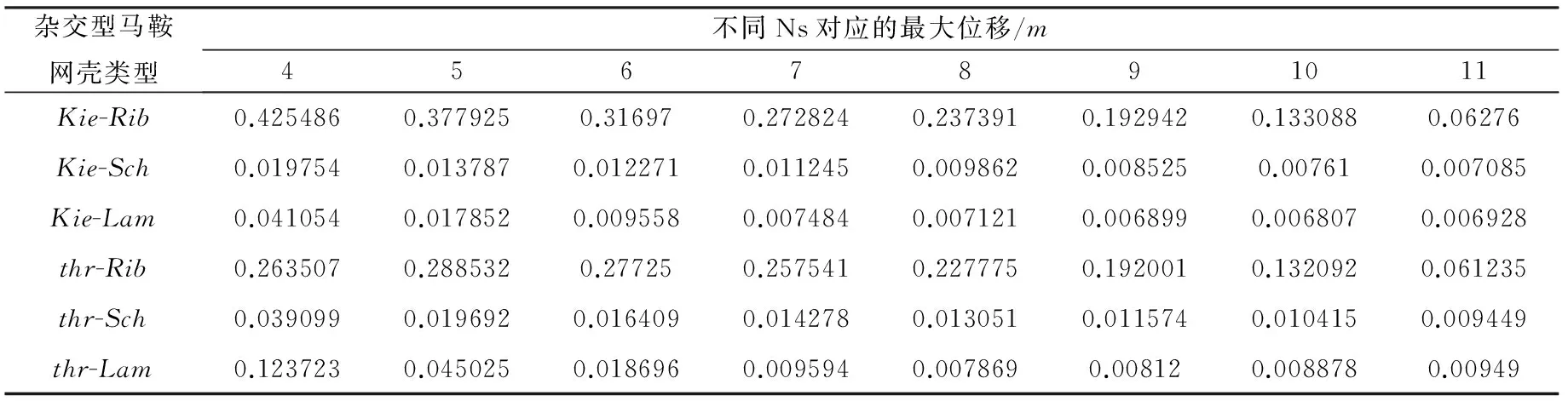
表1　六種網殼不同的Ns對應的最大位移

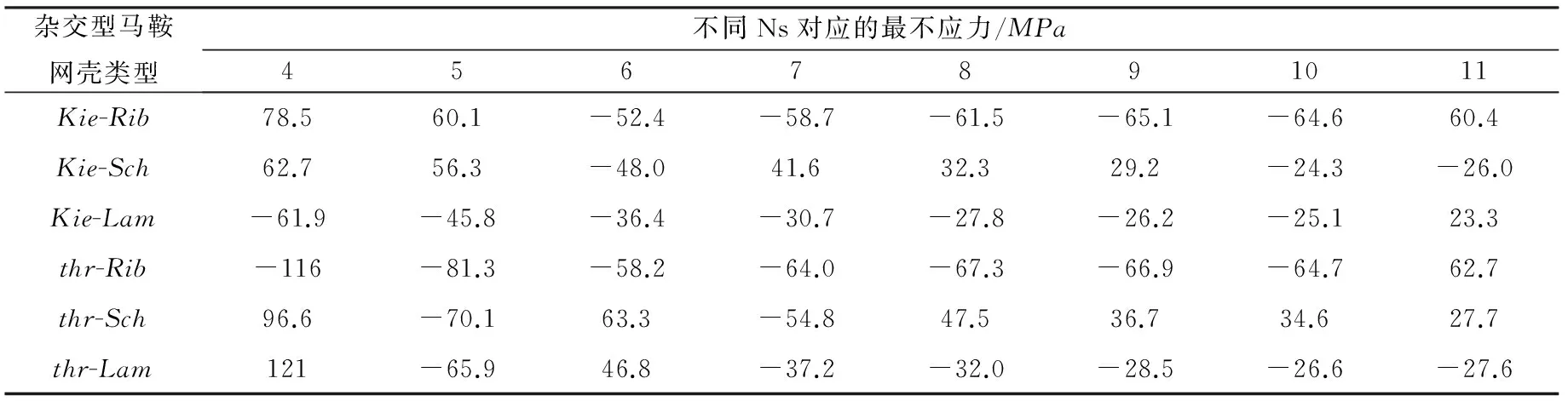
表2　六種網殼不同的Ns對應的最不利應力

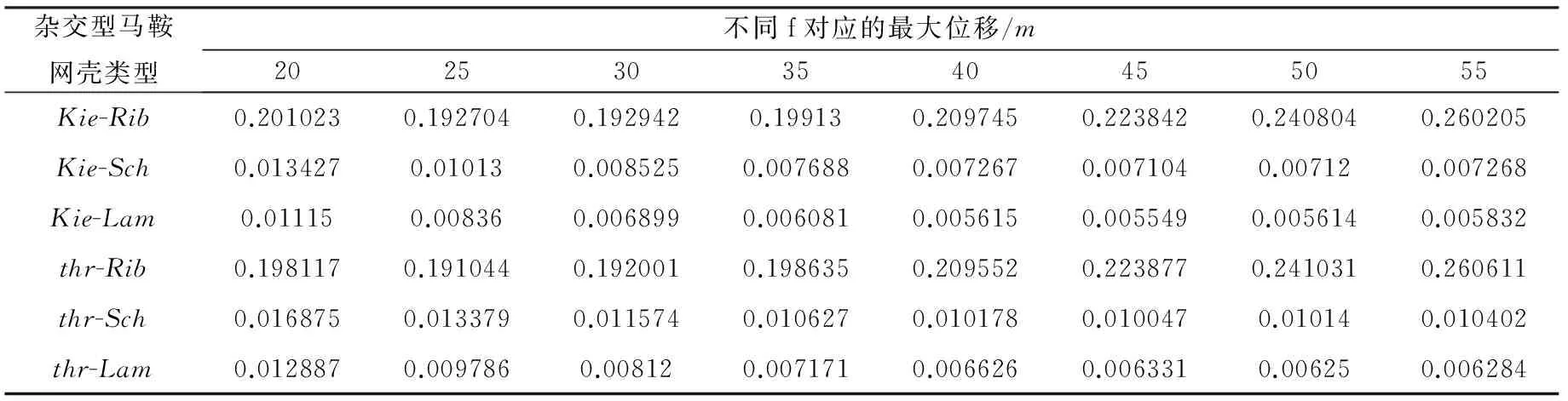
表3　六種網殼不同的f 對應的最大位移

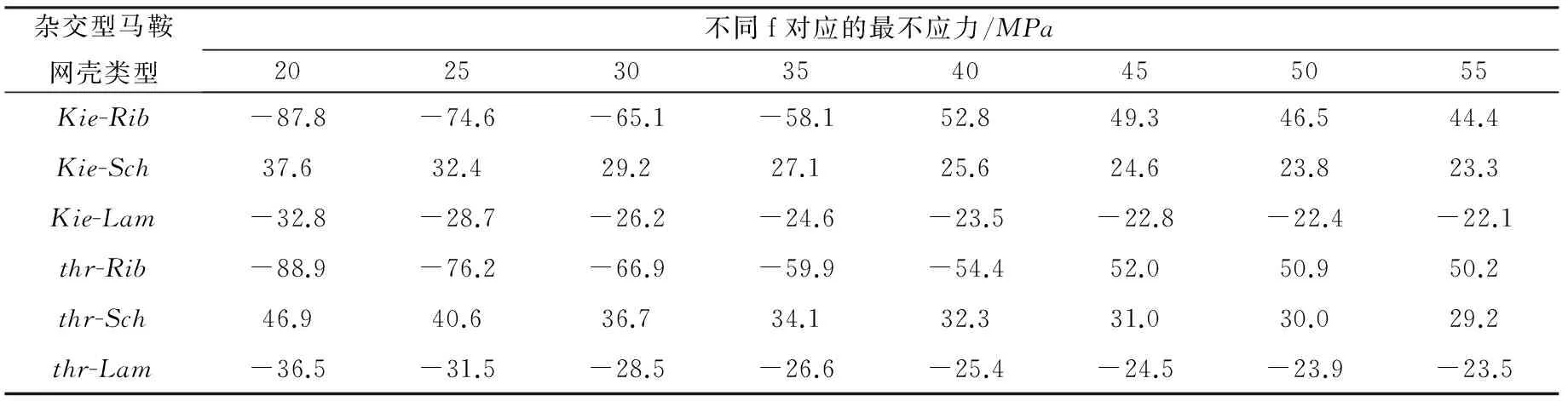
表4　六種網殼不同的 f 對應的最不利應力

通過上述表格可知：

(1) 由表1、2知，隨著Ns的增多：Kie-Lam和thr-Lam網殼的最大位移呈現先減小后增大的趨勢，其它四種雜交型馬鞍網殼的最大位移均呈現遞減的規律性變化，但變化幅度不是很大(最大幅度不超過毫米級)，但是Kie-Rib和thr-Rib網殼在Ns=4～9時最大位移均大于結構的允許位移0.15m，結構剛度已難以滿足實用要求；Kie-Rib、thr-Rib的最不利應力變化先減小后增大又變小波動性的變化，Kie-Sch、thr-Lam呈現先減小后增大的變化規律，而Kie-Lam、thr-Sch最不利應力則呈現遞減的變化規律。

(2) 由表3、4知，隨著f的增大，六種雜交型馬鞍網殼的最大位移均呈現先減小后增大的規律性變化，各自都存在結構合適矢高f使其整體位移最小；而最不利應力卻呈現遞減的規律性變化，Kie-Sch、thr-Sch以索向桿件受拉為主，Kie-Lam、thr-Lam以拱向桿件受壓為主，而Kie-Rib、thr-Rib矢高f較小時以拱向桿件受壓為主，f較大時以索向桿件受拉為主。f 每增加1m，最不利應力下降幅度最大的thr-Sch平均僅減少0.51MPa，相對下降1.08%，最不利應力下降幅度最小的Kie-Lam平均減少0.31MPa，相對下降0.93%(除Kie-Rib，thr-Rib外)，f增大對受力性能效果的改善并不顯著。

4　凱威特—聯方雜交型馬鞍網殼形狀優化分析

以網殼結構的Kn、Nx、Ns為設計變量，采用離散變量兩級形狀優化方法對其進行形狀優化，分析網格(Kn、Nx、Ns)變化對網殼結構耗鋼量的影響。

4.1基于離散變量兩級優化方法

第1級優化賦予初始桿件型鋼離散集中最小的截面尺寸和空心焊接球節點許用離散集最小型號，對其靜力分析，得到每組桿件的最不利應力，最大長細比等中間變量，增大桿件截面使其滿足應力、長細比，桿件局部穩定性和節點約束；第2級優化是以1級優化的解作為初始解，滿足結構整體位移和整體穩定性約束，滿足約束條件優化結束，否則，采用“相對差商法[13]”，增大“相對差商”最小的那組桿件截面和節點型號，讓全局約束條件得到滿足，又使整體結構耗鋼量增加最少，反復迭代直到全局約束全部滿足[14-16]。

4.2網殼形狀優化數學模型

設計變量：桿件截面積Ai(i=1，2，m1)，節點體積Vj(j=1，2，n)；目標函數網殼結構的最輕總重量由式(2)表示為

(2)

式中：m1為桿件組數；n為節點總數；Ai為第i 根桿件的面積，m2；Vj為第j個球節點的體積，m3；ρi、ρj分別為桿件和球節點鋼材的密度，kg/m3；li為第i根桿件的幾何長度，m；Vj=πD2t；D為球節點直徑，m；t為焊接空心球節點的壁厚，m。

應力約束：

(3)

式中：N為桿件軸力，N；A為桿件截面積，m2；My和Mz分別為繞局部二軸和局部三軸的彎矩，N·m；Wy和Wz分別為兩主軸的截面抗彎模量，m3；γy和γz為與截面模量相應的塑性發展系數，均取1.15，σ=215MPa為桿件的屈服應力。

彎矩作用平面內穩定性約束由式(4)表示為

(4)

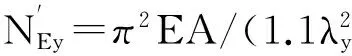
彎矩作用平面外穩定性約束由式(5)表示為

(5)

式中：φb為均勻彎曲的受彎構件整體穩定系數，取1.0；My為所計算構件段范圍內的最大彎矩，N·m；η為截面影響系數，閉口截面η=0.7,β1y為等效彎矩系數，取1.0。

長細比約束由式(6)表示為λ≤[λ]

(6)

式中:[λ]為桿件的長細比，壓桿取150，拉桿取250。

節點約束，空心球的最小直徑由式(7)表示為

(7)

式中：d1為兩相鄰鋼管中較大外徑，mm；ds為兩相鄰鋼管中較小外徑，mm；θ為兩相鄰桿件軸線間的夾角，rad；αn為兩相鄰鋼管間的凈距，一般取αn=10mm。

4.3數值算例

以受力性能較好的凱威特—聯方雜交型(Kie-Lam)馬鞍網殼為例進行形狀優化設計，給定S=60m、f=30m、Kn=6～16步長為2、Nx=10～12步長為1和Ns=4～9步長為1，共108個工況下，在結構滿足強度、剛度、局部穩定性和整體穩定性約束條件下，以網殼結構總耗鋼量最小為目標函數，尋求Kn、Nx和Ns最優組合，形狀優化得到的最優組合為Kn=8、Nx=12和Ns=8，總耗鋼量最小為27220.39kg。文中僅列出Kn分別為6、8、10和Nx為10～12、Ns為4～9時所對應的耗鋼量圖。

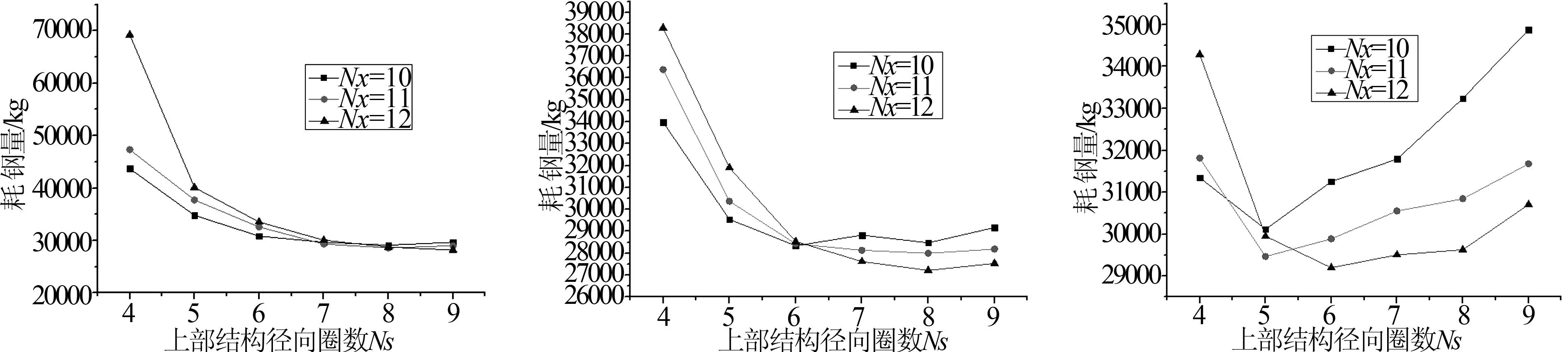
圖8　形狀優化對應的耗鋼量圖(a) Kn=6對應的耗鋼量；(b) Kn=8對應的耗鋼量；(c) Kn=10對應的耗鋼量

由圖8可知，當S =60m、f =30m時，Kie-Lam雜交型馬鞍網殼在滿足強度、剛度、穩定性前提下，Kn、Nx和Ns的匹配與網殼耗鋼量呈現較為復雜的非線性關系，網格數的變化對用鋼量比較敏感，特別當Ns=4變到Ns=5時，網殼耗鋼量下降均較大，最大下降量當屬Kn=6、Nx=12時達到50%左右。當Kn=6時，耗鋼量是隨著Ns的增加逐漸減小的，說明網殼桿件和節點增多的用鋼量相對于桿件截面變小的用鋼量的幅值偏小；當Kn>6 時，耗鋼量均隨著Ns的增加呈現先減小后增大的變化，受力合理的網格數一旦確定，則網格密度的增加是必會引起用鋼量的增加，但對網殼結構的受力性能改善并不大，一味的增大網格密度只會增加結構成本。網殼結構在形狀優化得到的最優網格數下既能保證結構安全性，又可獲得較高經濟效益，為降低實際工程造價提供了一條可靠途徑。

5　結論

文章對兩類六種雜交型馬鞍網殼進行了參數化設計，分析了S=60m時網殼靜力性能以及108種工況下Kie-Lam形狀優化，結果表明：

(1) 在f/s=1/2、Kn=6、Nx=12和Ns=9時，兩類網殼頂點處應力和位移均很小，避免了單一網殼頂點附近應力集中現象，Kie-Lam最大位移6.9mm和最不利應力25.1MPa均最小，受力合理，可優先選用，其次thr-Lam，Kie-Sch，thr-Sch。但是Kie-Rib和thr-Rib最大位移分別為192.9mm和192mm均大于結構允許撓度150mm，整體剛度較弱，不適合中大跨度結構。

(2) 最不利應力隨Ns變化沒有統一規律，卻與f成反比，f每增加1m最不利應力平均下降幅度最大為0.51MPa，相對降低1.08%(thr-Sch)對改善受力性能并不顯著；但存在合適f使其整體撓度各自最小，唯一Ns使Kie-Lam和thr-Lam整體撓度最小。

(3) 網格數對網殼耗鋼量影響較敏感，甚者可使其降低50%，當Kn=8、Nx=12和Ns=8時可保證Kie-Lam既安全同時總耗鋼量最輕，這為實際工程設計提供了有意的參考。

[1]鹿曉陽,趙曉偉,陳世英．離散變量網殼結構優化設計[M]. 北京：中國建筑工業出版社,2013.

[2]張志宏,李志強,董石麟．雜交空間結構形狀確定問題的探討[J]．工程力學,2010,27(11):56-62.

[3]張愛林,葛家琪,劉學春．2008奧運會羽毛球館大跨度新型弦支穹頂結構體系的優化設計選定[J]．建筑結構學報,2007, 28(6):1-4.

[4]王澈泉,申波,馬克儉,等．正三角形立體管桁架與單層柱面網殼雜交結構的設計與分析[J]．工業建筑,2014, 44(6):130-134.

[5]王毅,王雪生,朱忠義,等．中國石油大學(青島校區)體育館主館屋蓋結構選型與研究[J]．建筑結構,2009, 39(12):71-73．

[6]洪寧．拓展型球面網殼參數化建模與形狀優化設計[D]．濟南：山東建筑大學,2013.

[7]安然．橢圓水平投影雙曲拋物面網殼參數化設計及抗震性能分析[D]．濟南：山東建筑大學,2015.

[8]鹿曉陽,張萍,陳世英,等. 折板網殼結構參數化設計及受力特點分析[J]．山東建筑大學學報,2013,28(1):1-6．

[9]龔曙光,謝桂蘭．ANSYS參數化編程與命令手冊[M]．北京：機械工業出版社,2010.

[10]GB50009—2012，建筑結構荷載規范[S]．北京：中國建筑工業出版社,2012.

[11]JGJ7—2010，空間網格結構技術規程[S]．北京：中國建筑工業出版社,2010.

[12]張毅剛,薛素鐸,楊慶山，等．大跨空間結構[M]. 北京：機械工業出版社,2014.

[13]孫煥純,柴山,王躍方,等．離散變量結構優化設計[M]．大連：大連理工大學出版社,2002.

[14]陳世英,郭玉霞,鹿曉陽．單層球面網殼結構選型優化設計[J]．建筑鋼結構進展,2010,12(8):46-50．

[15]陳世英,鹿曉陽,綦文,等．凱威特網殼最優網格研究[J]．建筑鋼結構進展,2013,15(2):21-25．

[16]陳世英,鹿曉陽,王洪利,等．截面優化對網殼結構應力、位移和整體穩定性影響分析[J]．空間結構,2014, 20(1):45-52．

(學科責編：李雪蕾)

Parametric modeling and shape optimization ofhybridsaddlereticulatedshell

Su Ya1，Lu Shaobo2，Lu Xiaoyang1*,et al.

(1. Research Institute of Engineering Mechanics, Shandong Jianzhu University, Jinan250101, China；2．School of Architecture, Tampere University of Technology, FI-33720, Finland； 3. The First Design Department, Jinan Boiler Group Company?Limited, Jinan250022, China)

Hybridshellcantaketheadvantagesofeachsingletraditionalshell,whichcannotonlyincreasethespanbutalsoobtainhighereconomicbenefitsatthesametime.MacroprogramofsixkindshybridsaddlereticulatedshellparametricdesignweredevelopedbyANSYSparameterofdesignlanguageaccordingtosaddlereticulatedshellfeatures.Themechanicalperformanceswereanalyzedandtheshapeoptimizationunder108kindsofworkingconditionforKiewitt-LamellaSaddleReticulatedShellwasstudiedwithobjectivefunctionofminimumsteelconsumptionandshapeoptimizationdesignvariablesKn(ringtosymmetricregionalcopiesnumber), Nx(radialnoderingnumber), Ns(theupperstructureofradialring).Theresultsshowed:ThemaximaldisplacementandthemostunfavorablestressofKiewitt-Lamellawere6.9mmand25.1Mpa,whichweretheleastofsixkindshybridsaddlereticulatedshellthatitsmechanicalperformancewasthemostreasonableunderthesamecondition.Thevectorheightfwasinverselyproportionaltothemostunfavorablestress,existingsuitablefmadetheirrespectiveoveralldeflectionminimum,andNschangedthelawoftheunityonboth;WhenspanS=60mandthef=30mwerecertain,existingonekindofworkingconditionofKn=8, Nx=12andNs=8underthepreconditionsatisfiedthestrength,stiffnessandstability,makingthetotalsteelconsumptionofreticulatedshelllightest.

hybridsaddlereticulatedshell;parametricdesign;mechanicalperformancesanalysis;shapeoptimizationdesign

2015-12-06

山東省研究生創新計劃項目(SDYY08038);山東省自然科學基金項目(ZR2010AM016)

蘇亞(1987-)，男，在讀碩士，主要從事結構優化設計等方面的研究.E-mail：suya0310@163.com

*:鹿曉陽(1955-)，男，教授，博士，主要從事結構受力分析與優化設計、材料加工工藝等方面的研究.E-mail:lxy5504@yahoo.com.cn

1673-7644(2016)01-0038-09

TU393.3，TU311.41

A