基于藤copula–已實現GARCH的組合收益分位數預測

黃友珀,唐振鵬,唐　勇

(福州大學經濟與管理學院,福建福州350116)

基于藤copula–已實現GARCH的組合收益分位數預測

黃友珀,唐振鵬,唐勇

(福州大學經濟與管理學院,福建福州350116)

為準確預測分位數,利用已實現GARCH模型在邊緣分布建模中納入高頻信息,通過藤copula刻畫資產收益兩兩之間相異的相依結構,構建了資產組合收益分位數預測的藤copula–已實現GARCH模型.選取中國股市風格指數組合展開實證分析,回測檢驗結果表明高頻信息和異質相依結構是準確預測分位數的關鍵環節,藤copula–已實現GARCH模型能夠提供更準確的資產組合收益分位數預測.

分位數預測;藤copula–已實現GARCH;高頻信息;相依結構;回測檢驗

1　引　言

隨著經濟改革與發展,中國不斷推進金融自由化和全球化進程,逐步建成交易場所梯級化、交易產品多樣化、交易機制多元化的金融市場體系.金融資產價格的運動過程及其相依結構變得愈加復雜.為準確預測組合分位數并有效管理風險,市場參與者必須妥善處理價格過程及其相依結構的雙重復雜性.

資產價格過程的復雜性表現為波動集聚、偏峰厚尾、杠桿效應等典型事實(stylized facts),主要通過波動建模處理.波動率是一個必須通過可觀測數據估計的潛在變量.近20年來,利用高頻數據估計波動率已成為學界關注的焦點.在特定假設下,RV(realized volatility)是潛在波動率的一致估計量[1].在實踐中,存在導致RV有偏的問題.一是存在無法獲取高頻數據的非交易時間,如我國股市僅在上午9:30到11:30、下午1:00到3:00兩個時段交易,僅用4小時高頻數據計算得到的RV可能低估真實波動率.第二,隨著抽樣頻率提高,RV容易遭受市場微觀結構噪聲的影響[2].與許多偏差修正方法不同[3-5],Hansen等[6]提出對資產收益和RV聯合建模的已實現GARCH模型,能夠調整非交易時間和市場微觀結構噪聲導致的RV偏差.王天一和黃卓[7]進一步引入偏t分布,考慮了“偏峰厚尾”特征.這些工作為納入高頻信息的波動建模提供良好的框架,其優勢得到了實證的支持,如Watanabe[8]、Louzis等[9]、黃雯等[10].但已實現GARCH模型在資產組合分位數預測中的應用效果有待考證.

對于處理相依結構的復雜性,copula函數是一種靈活的工具.組合風險分析常用多元高斯copula[11,12]、學生t-copula[13,14]和阿基米德copula[15,16].其中,多元高斯copula可以描述非線性相依結構,但忽視了尾部相依.學生t-copula僅用一個自由度參數描述尾部相依,只能刻畫對稱的尾部相依.多元阿基米德copula能刻畫下尾相依或上尾相依,但同樣只有一個尾部相依參數.擴展阿基米德copula往往需要附加的參數限制,其建模靈活性受限.市場參與者往往持有風格或類別不同的資產構成的異質資產組合.成分資產兩兩之間的相依結構存在顯著差異,從而兩兩資產同時實現極端收益的概率也不同.因此,準確預測異質資產組合分位數要求相依結構模型能夠將對稱或非對稱的尾部相依以及兩兩相異的相依結構同時考慮在內.前述常用的多元copula隱含假設變量兩兩之間具有相同的相依結構,無法滿足這一要求. 藤copula由Bedford等[17,18]在Joe[19]的基礎上提出,利用藤結構將一系列二元copula函數聯結成多元copula函數,具有更強的相依結構建模靈活性[20-23].Aas等[20]系統研究藤copula函數的分解結構、參數估計和數值模擬問題,為藤copula的應用奠定了良好的基礎.近年來國內學者驗證了藤copula在不同領域的應用優勢,如唐振鵬和黃友珀[24],高江[25],郭文偉和鐘明[26],張幫正等[27]等.盡管文獻[25,26]已將藤copula應用于組合風險度量,但均未考慮高頻信息的影響.

可見,已實現GARCH和藤copula可能從波動率建模和相依結構刻畫兩個方面改進資產組合分位數預測方法.為此,本文將藤copula和已實現GARCH結合起來,提出預測資產組合收益分位數的藤copula–已實現GARCH模型,采用風格指數組合展開實證分析,在滾動時間窗口預測下結合多個回測檢驗(backtesting)指標驗證方法的有效性和優越性,為資產組合風險管理實踐提供參考.

2　資產組合分位數預測的藤copula–已實現GARCH方法

在給定置信水平(1-α)下,資產組合收益在第t天的向前一天VaRαt滿足

其中Ri,t+1指資產i的第t+1天收益率,(w1,w2,...,wN)代表成分資產在組合中的權重.

VaR是收益聯合分布的分位數,忽略了超出該分位數的尾部信息,應進一步考慮向前一天的資產組合收益ESαt,即

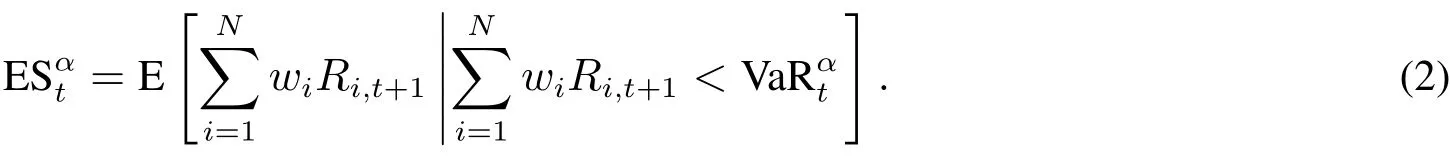
藤copula聯結邊緣分布得到的聯合分布往往不具有明確的解析式.通過藤copula預測資產組合收益分位數必須借助數值模擬方法獲得組合收益情景.從式(1)和式(2)看,組合收益是成分資產收益的簡單線性求和,成分資產相依結構體現在收益情景模擬中.換言之,為成分資產價格過程及其相依結構恰當建模是模擬情景貼近實際的前提.在邊緣分布建模中,通過已實現GARCH模型納入高頻信息,能夠濾出更接近現實的邊緣分布.另一方面,藤copula克服常用多元copula的缺陷,能夠充分考慮成分資產相依結構的異質性.這是構建藤copula–已實現GARCH模型的動機所在.

2.1資產收益邊緣分布

已實現GARCH模型引入已實現測度,信息含量更為豐富,可用于濾出分位數預測所需的邊緣分布.參考Hansen等[6],對數形式的已實現GARCH模型可以重寫為

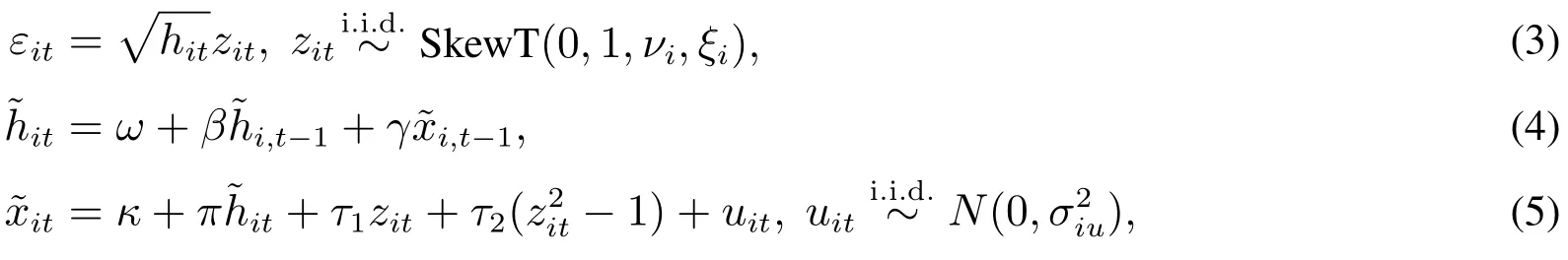
其中εit表示資產i在第t天扣除均值、消除自相關的殘差項,服從零均值、單位方差、自由度為νi、非對稱參數為ξi的偏t分布SkewT(0,1,νi,ξi)[8],i=1,2,...,N.it和t分別表示對數條件方差it=ln(hit)和對數已實現波動測度ln(xt).

2.2資產收益相依結構

藤copula的靈活性來源于兩個方面:分解結構和二元配對copula函數族.藤copula的分解結構是一種被稱為藤的圖形模型.實踐中常用的是C藤(canonical vine)和D藤(drawable vine).C藤和D藤分別通過基礎節點和基礎樹結構的選擇得到多樣的分解結構.基礎節點通常根據經濟含義確定,而基礎樹結構往往依據變量之間的秩相關排序選擇.在資產組合分位數預測中,難以確定何種成分資產起主導作用,而秩相關強弱排序是客觀的,因而D藤copula更適用.下面以四維D藤copula為例說明它的靈活性及其在異質資產組合分位數預測中的適用性.如圖1所示,1–2–3–4的基礎樹結構確定了惟一的D藤結構.

圖1　四維D藤copula分解結構示意Fig.1　Breakdown structure of four dimensional drawable vine copula

該結構下的四元聯合密度可以表示為

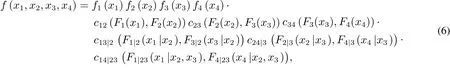
其中fi(·)是每個變量的密度函數,Fi(·)指每個變量的累積分布函數,i=1,2,3,4,j=1,2,3,4,F·|·(·|·)表示條件分布函數,cij(·,·)是copula的密度函數,c·|·(·|·)代表條件copula密度函數.

由圖1和式(6)可見:一方面,通過靈活選擇D藤結構,可以篩選出關鍵的配對變量(如12,23等)或條件配對變量(如13|2、24|3等),同時在結構上允許分別考慮配對變量的相依結構;另一方面,在選定的結構下,從豐富的二元copula函數族中選擇恰當的(條件)配對copula,能夠滿足(條件)配對變量相依結構刻畫的差異化需求.D藤copula的尾部相依取決于分解結構中所有配對copula的尾部相依參數,通過多個尾部相依參數充分考慮相依結構的異質性,尤其適用于異質資產組合收益分位數預測.

2.3藤copula–已實現GARCH方法的模型

藤copula聯結邊緣分布獲得的多元分布往往沒有明確的解析式,必須借助數值模擬預測組合分位數.首先利用已實現GARCH為資產收益建模,濾出邊緣分布;然后用藤copula刻畫資產收益的相依結構,利用藤copula–已實現GARCH模型模擬組合收益;最后預測分位數.用G(·)表示組合收益的聯合分布函數,Gi(·)表示第i個資產的邊緣分布函數(標準殘差分布),Cvine為藤copula函數,QF表示分位數預測值(VaR或ES),Q(·)表示不同分位數預測對應的函數,模擬資產組合收益為R(j),j=1,2,...,S,則有

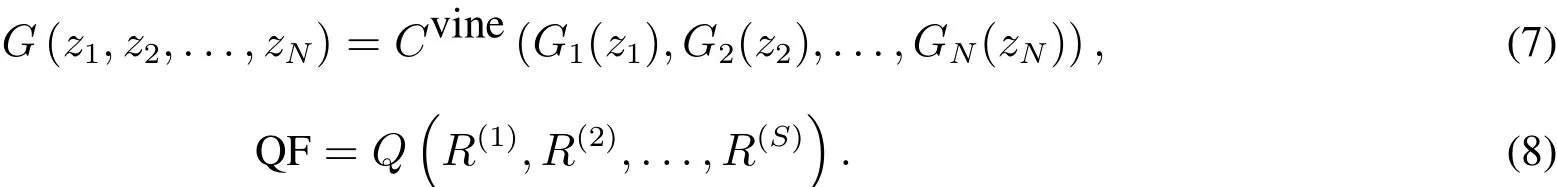
藤copula–已實現GARCH方法的模型可以通過聯立式(1)至式(8)表示.

2.4藤copula–已實現GARCH方法的應用步驟

步驟1成分資產邊緣分布建模.采用成分資產收益序列(Ri1,Ri2,...,RiT)和RV序列(RVi1,RVi2,..., RViT)估計已實現GARCH模型的參數,i=1,2,...,N;濾出資產收益的標準殘差向量(z1t,z2t,...,zNt), t=1,2,...,T,通過概率積分轉換獲得copula數據(G1(z1t),G2(z2t),...,GN(zNt)).

步驟2估計藤copula參數.以copula數據為基礎,采用較為成熟的極大似然法[20]估計藤copula的參數,即使用R軟件包CDVine估計參數[32],根據信息準則從豐富的二元copula函數族中選擇配對copula.

步驟3 模擬資產組合收益情景.首先,利用已估計參數的藤copula模擬隨機數,即生成獨立的、服從均勻分布U(0,1)的隨機向量(e1,e2,...,eN);然后令u1=e1,利用D藤copula分解結構中的條件copula函數得到等式ei=C(ui|u1,u2,...,ui-1),逐次求解該等式得到u2,u3,...,uN;其次,利用邊緣分布函數的逆函數將模擬數據轉換為資產收益標準殘差,并利用式(3)獲得成分資產i在第T+1天的模擬殘差εi,T+1,加回扣除的均值或自回歸項得到Ri,T+1,i=1,2,...,N.

步驟4預測資產組合收益分位數.重復進行S次步驟3,獲得成分資產i在第T+1天的模擬收益情景,i=1,2,...,N,根據式(1)和式(2)預測VaRαT和ESαT.

2.5資產組合收益分位數預測準確性評價

為驗證藤copula–已實現GARCH模型的有效性和優越性,相依結構建模考慮藤copula和常用多元copula(高斯copula、學生t-copula),波動建模考慮已實現GARCH模型與GJR-GARCH模型.為比較分位數預測效果, VaR的回測檢驗選用Kupiec[28]的非條件覆蓋率檢驗和Christoffersen[29]的條件覆蓋率檢驗.ES預測準確性利用D(α)值評估[30],即

D(α)越小,說明ES估計越準確.

3　實證分析

3.1數據基本分析

以巨潮風格系列指數(大盤價值、大盤成長、中盤價值、中盤成長、小盤價值和小盤成長)構成異質的風格資產組合.樣本數據包括2010年1月5日～2014年8月29日的日對數收益和5分鐘RV.巴塞爾協議建議風險度量模型的參數估計窗寬至少1年,即250個交易日左右.同時參考類似研究[25-27]，將樣本分為兩部分:樣本內數據(2010年1月6日～2013年6月7日,共828個交易數據)和樣本外數據(2013年6月13日～2014 年8月29日,共300個交易數據).樣本內數據用于估計藤copula–已實現GARCH模型參數,樣本外數據用于檢驗分位數預測的準確性.表1顯示,所有風格資產收益序列呈現負偏和尖峰形態,不服從正態分布.因此,實證假定標準殘差服從偏t分布.Ljung-Box Q檢驗說明中盤成長、小盤成長和小盤價值的收益序列存在自相關,而大盤成長、大盤價值和中盤價值不存在自相關.為獲得無自相關、扣除均值的殘差序列,用AR(1)為中盤成長、小盤成長和小盤價值指數收益建模,而大盤成長、大盤價值和中盤價值指數收益僅簡單扣除均值.風格資產的對數RV也不服從正態分布,因此為uit設定非正態分布可能是更好的選擇,這留待后續研究探討. LBQ(10)取值很大,說明風格資產的RV序列存在顯著自相關,即波動集聚效應.

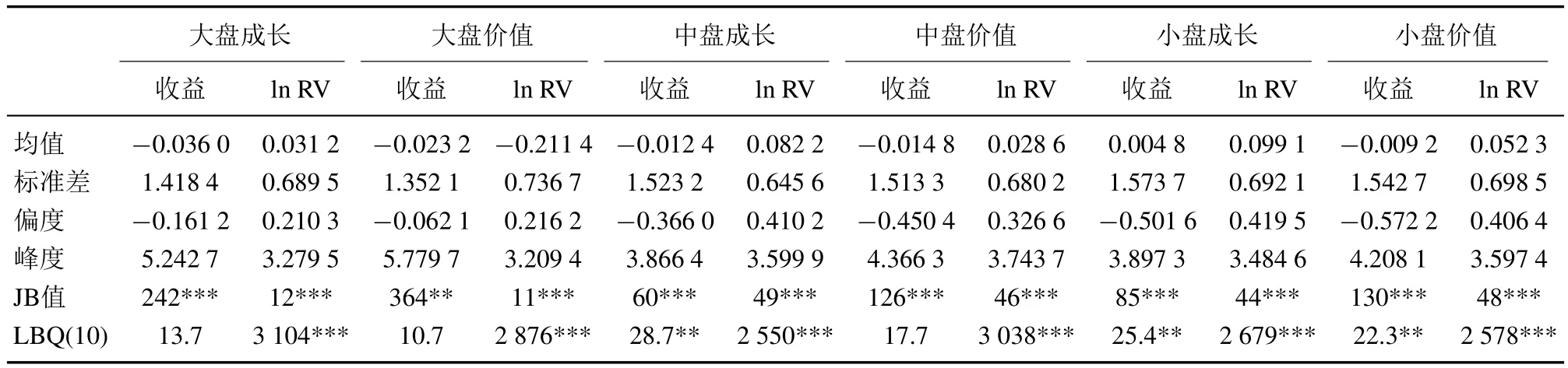
表1　資產收益及對數RV的描述性統計(2010–01–06～2014–08–19)Table 1 Descriptive statistics of asset returns and their ln RV

3.2藤copula–已實現GARCH模型的參數估計結果

已實現GARCH模型和GJR-GARCH模型的參數估計結果如表2和表3所示.β+πγ接近于1,說明風格資產收益序列具有很強的波動持續性.除了大盤價值,其他風格資產收益序列的τ1均小于0,與金融資產收益序列普遍存在杠桿效應的事實相符.

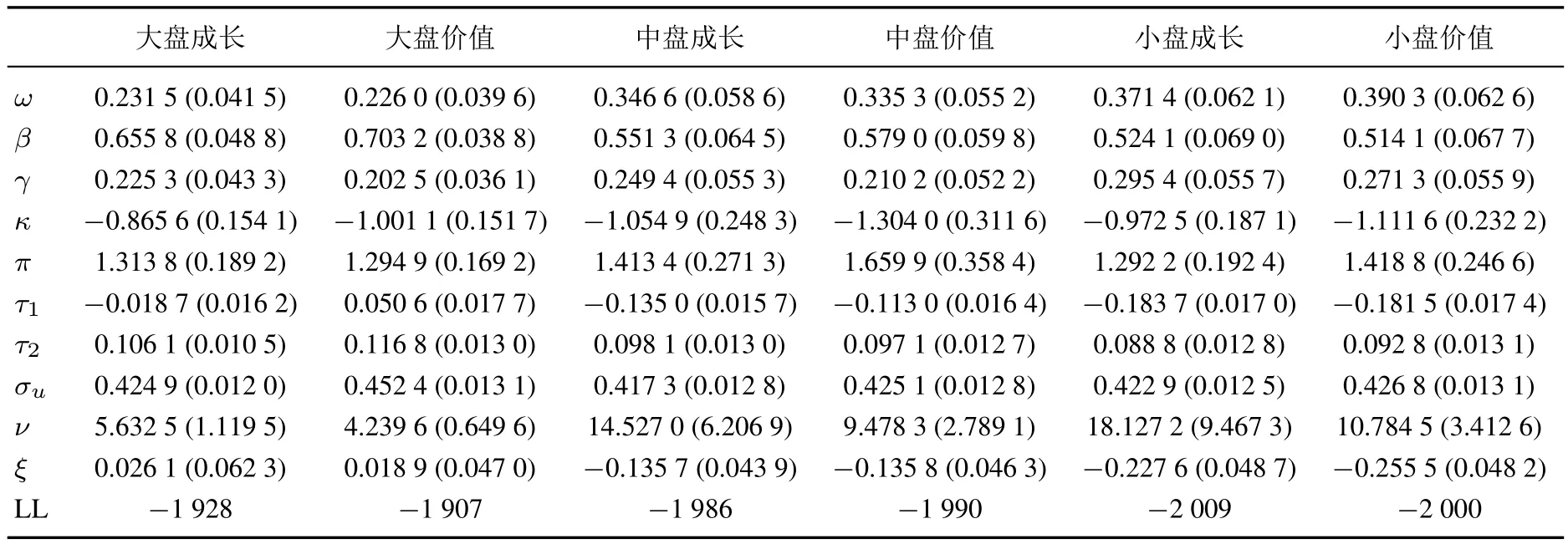
表2　已實現GARCH模型的參數估計結果Table 2 Parameter estimation of realized GARCH model

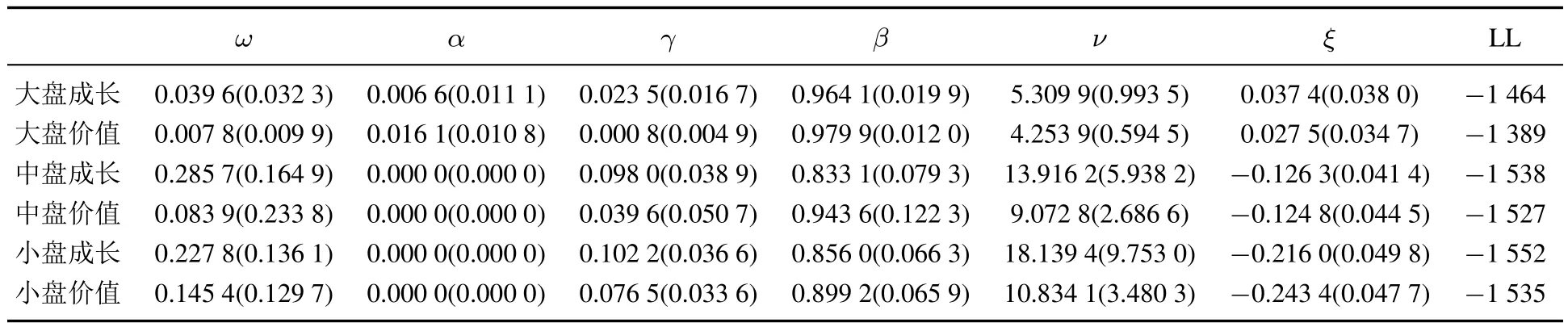
表3　GJR-GARCH模型的參數估計結果Table 3 Parameter estimation of GJR-GARCH model

標準殘差自相關檢驗和概率積分轉換序列的Kolmogorov-Smirnov(KS)和Cramer-von Mises(CvM)檢驗P值如表4所示.為避免參數估計誤差的影響,用bootstrap方法計算KS和CvM檢驗P值[31].所有P值大于0.1說明標準殘差無自相關,其概率積分轉換序列適用于藤copula建模.

表4　標準殘差序列的檢驗結果Table 4 Testing results of standardized residual series

為凸顯考慮成分資產收益相依結構差異的重要性,以常用的多元高斯copula(GC)和學生t-copula(TC)作為比較對象.表5和表6分別給出D藤copula和常用多元copula的參數估計結果.在表5中,1代表大盤成長,2為大盤價值,3為中盤成長,4為中盤價值,5為小盤成長,6為小盤價值,配對copula編號與文獻[32]保持一致.

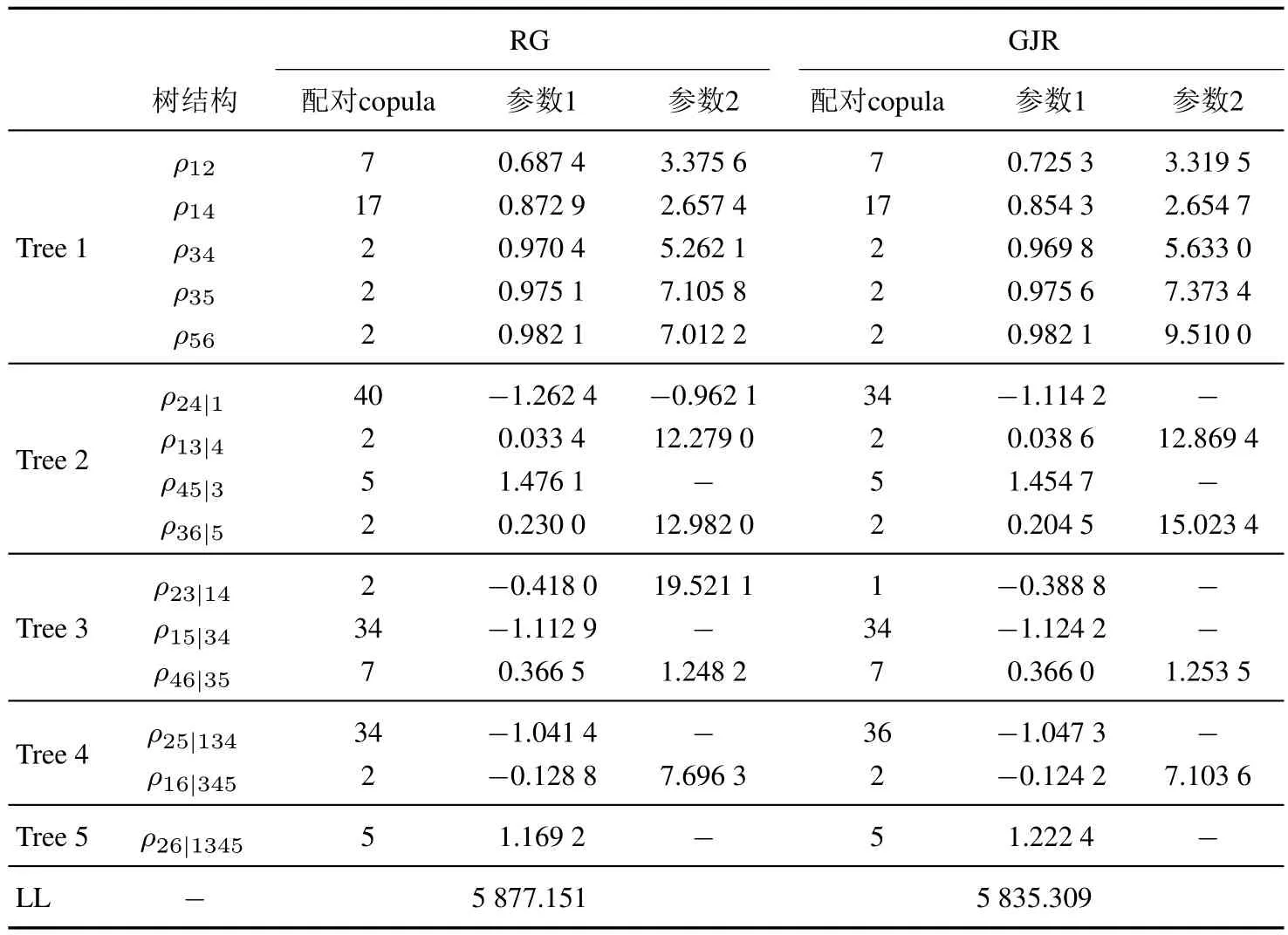
表5　D藤copula的分解結構與參數估計結果Table 5 Breakdown structure and parameter estimation of drawable vine copula

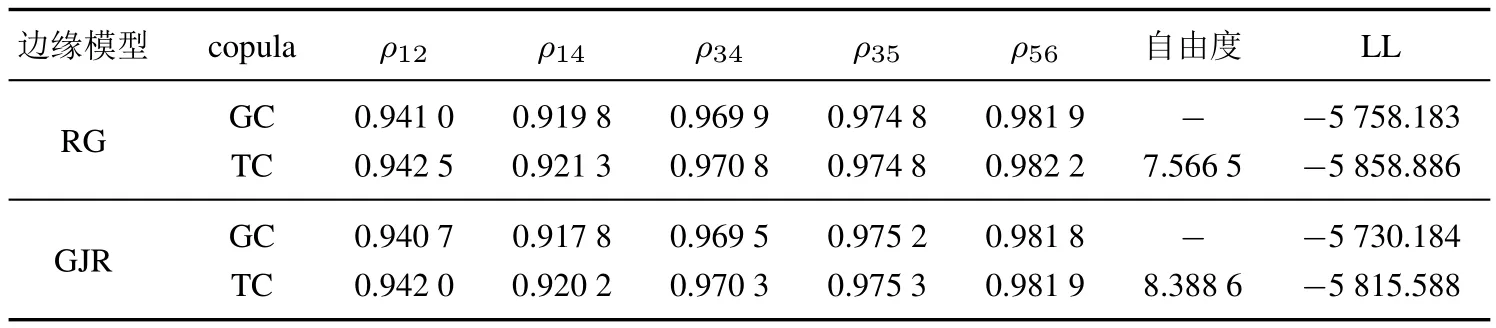
表6　常用多元copula的參數估計結果Table 6 Parameter estimation of commonly used multivariate copula

3.3資產組合收益的分位數預測結果

以3.2給出的參數估計結果為基礎,按照藤copula–已實現GARCH模型的應用步驟,采用滾動窗口法預測異質資產組合在樣本外300個交易日的分位數,其中異質資產組合由6個風格資產等權重構成.由表7可見,DV-GJR模型預測的95%置信水平下的VaR沒有通過似然比檢驗,而DV-RG模型在99%和95%兩個置信水平下的預測值均通過似然比檢驗,具有較好的表現.在ES預測中,基于DV-RG模型的ES具有更小的D(α)值.因此,在邊緣分布模型中考慮高頻信息能夠提高異質資產組合分位數預測的準確性.

表7　藤copula-GJR-GARCH與藤copula–已實現GARCH預測表現Table 7 Forecasting performance of vine copula-GJR-GARCH and vine copula-realized GARCH

表8列出不同copula–已實現GARCH模型的分位數預測表現.在VaR預測方面,t-copula–已實現GARCH模型在95%置信水平下未通過非條件似然比檢驗,其他模型和其他置信水平的VaR預測均通過了似然比檢驗,無法據此分辨模型優劣.但是,從極端尾部風險ES預測看,藤copula–已實現GARCH模型在99%和95%兩個置信水平下的ES預測均具有最小的D(α)值.

表8　不同copula–已實現GARCH模型的預測表現Table 8 Forecasting performance of different copula-realized GARCH model

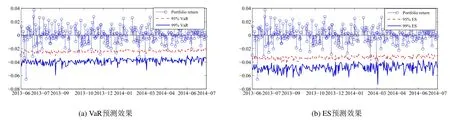
圖2　藤copula–已實現GARCH模型的分位數預測效果Fig.2　Quantile forecasting performance of vine copula-realized GARCH model

通過以上兩組對比,即選定D藤copula作為相依結構模型,比較已實現GARCH模型和GJR-GARCH模型;選定已實現GARCH作為邊緣分布模型,比較D藤copula、高斯copula和學生t-copula模型,結果表明藤copula–已實現GARCH模型在99%和95%兩個置信水平下均提供了更準確的分位數預測,尤其是在極端尾部風險ES預測方面,藤copula–已實現GARCH模型的優勢尤為顯著.參考已有研究的做法[25,26],進一步用圖2直觀展示藤copula–已實現GARCH模型的VaR和ES的預測效果.

表7、表8和圖2展示的結果證實了資產組合分位數預測的藤copula–已實現GARCH方法的優越性.基于第2部分闡述的建模動機,著重從兩個方面解釋這一優越性.首先,已實現GARCH模型同時引入已實現測度和杠桿函數,由它導出的條件波動率包含了交易時段內的高頻信息和非交易時段的波動信息,具有明顯的信息含量優勢.其次,資產組合的成分資產收益序列存在異質性.這種異質性不僅體現在不同資產收益序列的邊緣分布中,更體現在不同資產收益序列之間的相依結構中.常用多元copula(如多元高斯copula或學生t-copula)隱含假定成分資產收益序列兩兩之間的相依結構類型和相依程度都是相同的.但是,正如實證結果所呈現出來的那樣，如第一層樹對應的配對copula向量、Kendallτ向量和下尾相依系數向量分別為(7,17,2,2,2),(0.78,0.74,0.84,0.86,0.88)及(0.74,0.70,0.77,0.76,0.79),均存在顯著差異.成分資產收益之間的相依結構具有常用多元copula函數無法刻畫的異質性.而藤copula通過靈活選擇藤分解結構和配對copula能夠充分考慮相依結構的異質性.從不同copula函數的極大似然函數值可以簡單看出(表5和表6), 藤copula具有最佳的擬合效果.同時,從不同組合收益分位數預測結果看(表7和表8),基于藤copula的新方法無論在VaR預測還是ES預測中都具有較好的表現.由此可見,在六維情形下,藤copula已經展現出一定優勢.在高維情形下,相依結構的異質性隨著維數增加而增強,藤copula的優勢將進一步凸顯[21].但是,高維情形的藤copula參數估計和數值模擬也會變得更加復雜.另外,在多期分位數預測中[33],藤copula–已實現GARCH方法同樣會遭遇模擬復雜性問題.因此,如何在高維資產組合分位數預測和多期分位數預測應用中權衡藤copula的建模靈活性與計算復雜性是一個亟待后續研究探討的問題.

4　結束語

資產組合的成分資產收益序列本身存在波動集聚、偏峰厚尾、杠桿效應等復雜特征,資產收益序列之間的相依結構復雜性體現為非線性、非對稱、尾部相依以及收益序列兩兩之間相依結構的異質性.本文妥善處理資產收益序列及其相依結構的雙重復雜性,利用已實現GARCH模型和藤copula同時改進邊緣分布建模和相依結構建模,提出預測資產組合收益分位數的藤copula–已實現GARCH模型.中國股市風格指數組合的實證分析結果表明:在邊緣分布納入高頻信息有助于提高分位數預測精度;風格指數收益之間的相依關系存在結構性差異,藤copula能更恰當地描述它們之間復雜的相依關系;藤copula–已實現GARCH模型在實證中提供較好的資產組合收益分位數預測.藤copula–已實現GARCH模型的優勢來源于納入高頻信息和藤copula在相依結構建模中的靈活性.這些結論對金融市場機構投資者、個體投資者以及政策制定者均有一定借鑒意義:第一,機構投資者和個體投資者要有效管理資產組合風險,一方面應監測高頻波動信息,另一方面應根據資產收益之間的復雜相依結構調整資產的配置比例,即根據相依結構特征選擇投資組合[27];第二,政府相關部門在制定政策時應充分認識到不同類別資產之間存在的非線性、非對稱性和尾部相依特征,更準確地預估政策影響,從而制定合理的市場規則或監管政策,最終有效控制系統性風險、維護金融市場的穩定.

[1]Andersen T G,Bollerslev T.Answering the skeptics:Yes,standard volatility models do provide accurate forecasts.International Economic Review,1998,39(4):885–905.

[2]Hasbrouck J.Empirical Market Microstructure:The Institutions,Economics and Econometrics of Securities Trading.New York: Oxford University Press,2007:31–41.

[3]Hansen P R,Lunde A.A forecast comparison of volatility models:Does anything beat a GARCH(1,1).Journal of Applied Econometrics,2005,20(7):873–889.

[4]Bandi F M,Russell J R.Microstructure noise,realized variance,and optimal sampling.Review of Economic Studies,2008,75(2): 339–369.

[5]Barndorff-Nielsen O E,Hansen P R,Lunde A,et al.Designing realized kernels to measure the ex post variation of equity prices in the presence of noise.Econometrica,2008,76(6):1481–1536.

[6]Hansen P R,Huang Z,Shek H H.Realized GARCH:A joint model for returns and realized measures of volatility.Journal of Applied Econometrics,2012,27(6):877–906.

[7]王天一,黃卓.高頻數據波動率建模:基于厚尾分布的Realized GARCH模型.數量經濟技術經濟研究,2012(5):149–161. Wang T Y,Huang Z.High frequency volatility modelling based on realized GARCH model with heavy-tailed distribution.TheJournal of Quantitative&Technical Economics,2012(5):149–161.(in Chinese)

[8]Watanabe T.Quantile forecasts of financial returns using realized GARCH models.Japanese Economic Review,2012,63(1):68–80.

[9]Louzis D P,Xanthopoulos-Sisinis S,Refenes A P.The role of high-frequency intra-daily data,daily range and implied volatility in multi-period value-at-risk forecasting.Journal of Forecasting,2013,32(6):561–576.

[10]黃雯,王天一,黃卓.利用高頻數據管理滬深300指數的尾部風險:基于Realized GARCH模型的VaR.中大管理研究,2012, 7(2):66–86. Huang W,Wang T Y,Huang Z.Managing HS 300 index tail risk with high frequency data:Value-at-risk based on realized GARCH approach.China Management Studies,2012,7(2):66–86.(in Chinese)

[11]韋艷華,張世英.多元copula-GARCH模型及其在金融風險分析上的應用.數理統計與管理,2007,26(3):432–439. Wei Y H,Zhang S Y.Multivariate copula-GARCH model and its applications in financial risk analysis.Journal of Applied Statistics and Management,2007,26(3):432–439.(in Chinese)

[12]周孝華,張保帥,董耀武.基于Copula-SV-GPD模型的投資組合風險度量.管理科學學報,2013,15(12):70–78. Zhou X H,Zhang B S,Dong Y W.Risk measurement of financial portfolio based on copula-SV-GPD model.Journal of Management Sciences in China,2013,15(12):70–78.(in Chinese)

[13]胡心瀚,葉五一,繆柏其.基于Copula-ACD模型的股票連漲和連跌收益率風險分析.系統工程理論與實踐,2010,30(2): 298–304. Hu X H,Ye W Y,Miao B Q.Risk analysis of continuously rising and falling stock yield based on copula-ACD method.Systems Engineering:Theory&Practice,2010,30(2):298–304.(in Chinese)

[14]謝赤,朱建軍,周竟東.基于Copula函數的ETF流動性風險與市場風險相依性分析.管理科學,2010,23(5):94–102. Xie C,Zhu J J,Zhou J D.Dependence analysis of liquidity risk and market risk for exchange traded funds based on copula function. Journal of Management Science,2010,23(5):94–102.(in Chinese)

[15]吳慶曉,劉海龍,龔世民.基于極值Copula的投資組合集成風險度量方法.統計研究,2011,28(7):84–91. Wu Q X,Liu H L,Gong S M.Integrated risk measurement of portfolio with extreme copula.Statistical Research,2011,28(7): 84–91.(in Chinese)

[16]陸靜,張佳.基于極值理論和多元Copula函數的商業銀行操作風險計量研究.中國管理科學,2013,21(3):11–19. Lu J,Zhang J.Measurement of commercial bank’s operational risk based on extreme value theory and multivariate copula functions. Chinese Journal of Management Science,2013,21(3):11–19.(in Chinese)

[17]Bedford T,Cooke R M.Probability density decomposition for conditionally dependent random variables modeled by vines.Annals of Mathematics and Artificial Intelligence,2001,32(1/4):245–268.

[18]Bedford T,Cooke R M.Vines:A new graphical model for dependent random variables.The Annals of Statistics,2002,30(4): 1031–1068.

[19]Joe H.Families of m-variate distributions with given margins and m(m-1)/2 bivariate dependence parameters//Ruschendorf L, Schweizer B,Taylor M D Eds.Lecture Notes-Monograph Series:Distributions with Fixed Marginals and Related Topics.Bethesda: Institute of Mathematical Statistics,1996:120–141.

[20]Aas K,Berg D.Models for construction of multivariate dependence:A comparison study.The European Journal of Finance,2009, 15(7–8):639–659.

[21]Fisher M,K¨ock C,Schl¨uter S,et al.An empirical analysis of multivariate copula models.Quantitative Finance,2009,9(7):839–854.

[22]Low R K Y,Alcock J,Faff R,et al.Canonical vine copulas in the context of modern portfolio management:Are they worth it. Journal of Banking&Finance,2013,37(8):3085–3099.

[23]Zhang B,Wei Y,Yu J,et al.Forecasting VaR and ES of stock index portfolio:A vine copula method.Physica A:Statistical Mechanics and Its Applications,2014,416:112–124.

[24]唐振鵬,黃友珀.組合信用風險測度的藤copula方法.系統工程學報,2013,28(4):488–496. Tang Z P,Huang Y P.Vine copula approach to measure portfolio credit risk.Journal of Systems Engineering,2013,28(4):488–496. (in Chinese)

[25]高江.藤copula模型與多資產投資組合VaR預測.數理統計與管理,2013,32(2):247–258. Gao J.Vine copula model and VaR forecast for multi-asset portfolio.Journal of Applied Statistics and Management,2013,32(2): 247–258.(in Chinese)

[26]郭文偉,鐘明.基于Vine Copula的中國股市風格資產相依結構特征及組合風險測度.管理評論,2013,25(11):41–52. Guo W W,Zhong M.An empirical study on dependency structure and risk measure of style portfolio in Chinese stock market based on vine copula model.Management Review,2013,25(11):41–52.(in Chinese)

[27]張幫正,魏宇,余江,等.基于EVT-Vine-copula的多市場相關性及投資組合選擇研究.管理科學,2014,27(3):133–144. Zhang B Z,Wei Y,Yu J,et al.The study of correlation and portfolio selection among multi-markets based on EVT-vine-copula. Journal of Management Science,2014,27(3):133–144.(in Chinese)

[28]Kupiec P.Techniques for verifying the accuracy of risk management models.Journal of Derivatives,1995,3(2):73–84.

[29]Christoffersen P F.Evaluating interval forecasts.International Economic Review,1998,39(4):841–862.

[30]Embrechts P,Kaufmann R,Patie P.Strategic long-term financial risks:Single risk factors.Computational Optimization and Applications,2005,32(1–2):61–90.

[31]Patton A.Copula methods for forecasting multivariate time series//Elliott G,Timmermann A eds.Handbook of Economic Forecasting.Amsterdam:Elsevier,2013,2(B):899–960.

[32]Brechmann E C,Schepsmeier U.Modeling dependence with C-and D-vine copulas:The R package CDVine.Journal of Statistical Software,2013,52(3):1–27.

[33]許啟發,張金秀,蔣翠俠.基于支持向量分位數回歸多期VaR測度.系統工程學報,2014,29(2):202–214. Xu Q F,Zhang J X,Jiang C X.Evaluating multiperiod VaR via support vector quantile regression.Journal of Systems Engineering, 2014,29(2):202–214.(in Chinese)

Portfolio quantile forecasts based on vine copula and realized GARCH

Huang Youpo,Tang Zhenpeng,Tang Yong
(School of Economics and Management,Fuzhou University,Fuzhou 350116,China)

Aiming at enhancing quantile forecasting performance,this article incorporates high-frequency information using realized GARCH model,then captures the variant dependency structure of pairs of asset returns by vine copula,and constructs a quantile forecasting approach based on vine copula-realized GARCH model.Selecting Chinese style index portfolio to carry out an empirical analysis,the backtesting results show that both high-frequency information and heterogenous dependency structure are key links for precise quantile forecasts,and the proposed method provides more accurate quantile forecasts of portfolio returns.

quantile forecast;vine copula-realized GARCH;high-frequency information;dependency structure;backtesting

F830

A

1000-5781(2016)01-0045-10

10.13383/j.cnki.jse.2016.01.005

2014-12-16;

2015-06-25.

國家自然科學基金資助項目(71171056);福建省社科規劃辦重點資助項目(2013A017);福建省高等學校新世紀優秀人才支持計劃資助項目(JA11025S).

黃友珀(1987—),男,福建泉州人,博士生,研究方向:金融風險度量及管理,Email:fzuhyp@126.com;

唐振鵬(1966—),男,湖北鐘祥人,博士,教授,博士生導師,研究方向:金融工程,Email:zhenpt@126.com;

唐勇(1970—),男,江蘇洪澤人,博士,教授,研究方向:金融計量與風險管理,Email:tangyong05@126.com.