光纖環瞬態溫度梯度對Shupe誤差的影響
劉國軍,章 博,潘 雄
(北京航空航天大學儀器科學與光電工程學院,北京100191)
光纖環瞬態溫度梯度對Shupe誤差的影響
劉國軍,章 博,潘 雄
(北京航空航天大學儀器科學與光電工程學院,北京100191)
光纖陀螺的承環結構不同,會影響光纖環的溫度及溫度梯度分布,進而影響陀螺的精度。對四種不同承環結構的光纖陀螺進行有限元瞬態熱仿真,得到光纖環的溫度分布。基于四極對稱繞法繞制光纖環的截面數字離散化模型,繪制了四個光纖環沿展開光纖上的溫度分布,計算了四個陀螺的軸向和徑向溫度梯度及其引起的Shupe誤差。對比分析結果表明:承環結構形式不同,光纖環的軸向和徑向溫度梯度不同,軸向溫度梯度對光纖環的Shupe誤差影響更大。
光纖環;承環結構;徑向向溫度梯度;軸向溫度梯度;Shupe誤差
0 引言
光纖陀螺由光路組件、電路組件和機械結構組成。各組件均對環境溫度變化敏感,尤其是作為敏感元件的光纖環[1]。環境溫度主要通過機械結構傳至光纖環,因此機械結構與光纖環的接觸方式不同會影響光纖環的溫度以及溫度梯度分布,進而影響陀螺的精度[2]。陀螺內容納、支撐和保護光纖環,為光纖環敏感軸方向提供基準,且與光纖環溫度和振動特性有密切關系的部分機械結構稱為承環結構。
目前有很多文獻對承環結構的結構形式及其材料屬性對光纖環溫度性能的影響進行了定性分析,并給出了具體的改進措施,但沒有定量分析表征光纖環溫度分布均勻性的徑向溫度梯度、軸向溫度梯度以及周向溫度梯度對光纖環溫度性能的影響。P.B.Ruffin等研究了軸向和徑向溫度梯度對光纖環Shupe誤差的影響,指出四極對稱繞法繞制的光纖環對軸向溫度梯度更敏感[3-4]。本文在P.B.Ruffin等的研究基礎上,以某一型號四種不同承環結構的陀螺為研究對象,定量分析軸向和徑向溫度梯度對光纖環溫度性能的影響。
目前實際應用中陀螺的承環結構的材料主要是鋁合金,結構形式主要有C字型、L字型、I字型和一字型四種,如圖1所示。這四種承環結構與光纖環的接觸方式不同(從三邊接觸到一邊接觸),環境溫度經過承環結構傳至光纖環的路徑不同,導致光纖環截面的軸向和徑向溫度梯度不同,定量分析它們對光纖環溫度性能的影響,對光纖陀螺結構設計具有一定的指導意義。

圖1 光纖環的四種安裝方式及其簡化示意圖Fig.1 Four kinds of installation methods of optical fiber ring
1 熱致非互易誤差理論
根據Shupe誤差原理和Mohr公式[5-7],取一小段光纖為微元(dz),當存在溫度擾動時,光沿這段光纖傳播的相位變化:

式中,β0為光在光纖中的傳播常數,n為光纖折射率,?n/?T為光纖折射率隨溫度變化系數,ΔT為這段光纖上的溫度變化量。沿光纖長度積分,得到Sagnac干涉儀中兩束反向傳輸的光產生的相移及相移差:

由此可得由溫度瞬態效應引起的旋轉角速率誤差:

式中,D為光纖環的有效直徑(光纖環內外徑均值),L為光纖長度。
2 有限元瞬態熱仿真與實驗
2.1有限元仿真
模型和材料參數:光纖環的溫度分布主要取決于環境溫度和承環結構,建模時可以只考慮承環結構和光纖環兩部分。基于旋轉對稱性,可以按其截面建模,將三維模型簡化為二維模型,如圖2所示。
有限元模型中各部分的材料參數如表1所示。

圖2 模型簡化過程Fig.2 Simplification of the model

表1 材料參數Table 1 Material parameter
載荷和邊界條件:有限元仿真時,為了模擬溫箱內傳熱情況,溫度載荷與實驗溫度一致。由于溫箱內的氣流由風扇驅動,陀螺表面的對流屬于強制對流。通常溫箱內的風速范圍為2.5m/s~3m/s,取μ= 2.5m/s時,對流換熱系h=16W/(K·m2)[8]。
2.2溫度實驗
為了驗證有限元模型的有效性,需要進行溫度實驗。設定實驗溫度為:初始溫度為25℃,實驗開始后以1℃/min的溫變速率降溫至-40℃,保溫1h,再以1℃/min的溫變速率升溫至60℃,保溫55min,實驗結束。總時間為280min(16800s)。實驗結果如圖3所示,實測溫度曲線與仿真溫度曲線基本吻合,驗證了模型的正確性。

圖3 溫度曲線Fig.3 Temperature curve
2.3仿真結果
瞬態熱仿真得到光纖環截面在溫度實驗時間內每一時刻的溫度分布。t=9600s時刻,四種結構下光纖環截面的溫度分布如圖4所示。N.01和N.03光纖環的溫度分布上下對稱(軸向對稱),N.04光纖環的溫度分布左右對稱(徑向對稱)。

圖4 四種結構下光纖環截面的溫度分布Fig.4 Temperature distribution of four fiber ring sections

圖5 光纖環截面離散化模型Fig.5 Discrete model of fiber ring section
3 溫度梯度引起的Shupe誤差
3.1沿光線長度的溫度分布
基于光纖環圓周方向溫度均勻分布的假設,光纖環每一圈光纖可以由環截面一個節點表示,如圖5所示。光纖環的幾何參數:環內徑R= 45mm,環寬W=12mm,環高H=27mm,層數M=52,匝數N=108,光纖直徑d=250μm。結合環截面離散化模型和溫度仿真結果,可以得到每一圈光纖的溫度和位置。將這兩者對應起來便得到沿光纖長度的溫度分布T(z,t)。t=9600s時刻的溫度分布曲線如圖6所示。

圖6 光纖上的溫度分布Fig.6 Temperature distribution along the fiber
3.2軸向和徑向溫度梯度
圖6中每一個小拋物線為每一層光纖的溫度分布,即光纖環的軸向溫度分布。t時刻小拋物線的最大幅值A為光纖環軸向溫差ΔTa(t)下包絡線反映光纖環的徑向溫度分布。t時刻下包絡線的幅值B為光纖環徑向溫差ΔTr(t)四種結構下光纖環的軸向和徑向溫差隨時間變化曲線,如圖7所示。四種結構下光纖環的軸向溫差最大值分別為: 3.03℃、3.37℃、1.13℃、6.18℃;徑向溫差最大值分別為:2.84℃、3.26℃、3.35℃、1.42℃。

圖7 四種結構下光纖環的軸向和徑向溫差Fig.7 Axial and radial temperature difference of four fiber rings
根據梯度定義,環截面任一點處的溫度梯度以及軸向、徑向溫度梯度分量分別為:
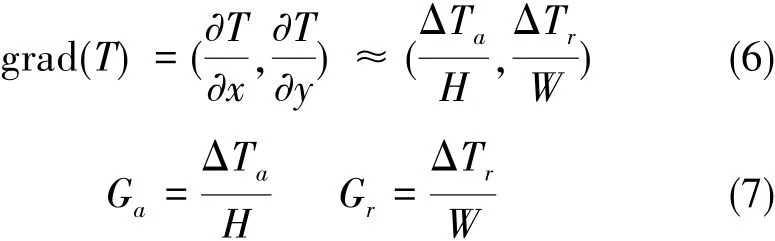
3.3Shupe誤差
根據式(5)計算得到軸向和徑向溫度梯度引起的旋轉速率誤差隨時間變化曲線Ω(t),如圖8所示。四種結構下光纖環的旋轉速率誤差最大值分別為:0.0383(°)/h、0.0495(°)/h、0.0089(°)/h、0.1047(°)/h。

圖8 旋轉角速率誤差隨時間變化Fig.8 Variation of rotational rate error with time
3.4誤差與溫度梯度的關系
結合圖7和圖8可知,由熱擾動引起的旋轉速率誤差分別與軸向和徑向溫差成正比,如圖9所示,即軸向和徑向溫差越大,由它們引起的誤差越大。對每一個陀螺有:Ω=K1ΔTa,Ω=K2ΔTr,所以旋轉速率誤差與軸向溫度差和徑向溫度差滿足關系式:


圖9 四個環的軸向、徑向溫差與誤差的關系Fig.9 Relationship between the axial and radial temperature difference of four fiber rings and the rotational rate error
將軸向溫度差、徑向溫度差以及由其引起的誤差進行多項式曲面擬合,如圖10所示,得到旋轉速率誤差Ω關于軸向溫度差ΔTa和徑向溫度差ΔTr的函數關系式:
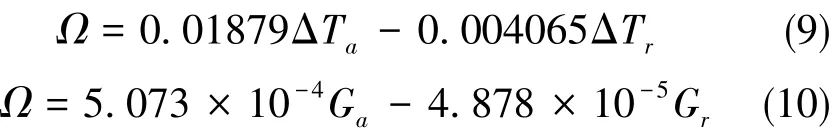
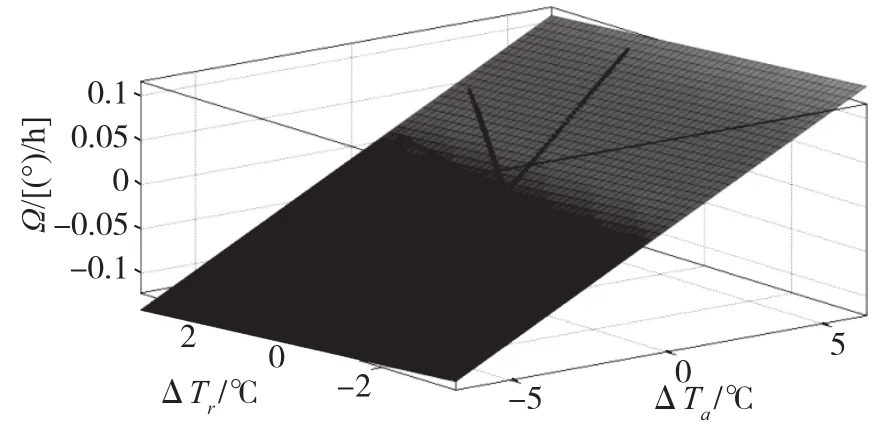
圖10 軸向、徑向溫差和誤差的關系式擬合Fig.10 Fitting of relationship between axial temperature difference,radial temperature difference and rate error
4 結果分析
式(10)中,Gr項的系數4.878×10-5比Ga項的系數5.073×10-4小一個數量級,說明徑向溫度梯度引起的誤差相比軸向溫度梯度引起的很小,Shupe誤差主要來源于軸向溫度梯度。這是因為四極對稱繞法對徑向溫度梯度實現了兩次抵消,第一次抵消:對稱段的溫度差;第二次抵消:相鄰兩對稱段的溫度差異號,如圖11所示。

圖11 徑向溫度差相消過程Fig.11 The radial temperature difference cancellation
四個光纖環的軸向、徑向最大溫差以及誤差極值列表如表2所示。

表2 結果列表Table 2 Result lists
對比分析四種情況可知:1)旋轉速率誤差對軸向溫度梯度更敏感,即軸向溫度梯度越大,誤差越大;2)軸向溫度對稱分布能在一定程度上減小誤差。
仿真結果表明承環結構與光纖環內側單邊接觸時(N.03),溫度梯度引起的誤差最小。這一結果與文獻[4]、文獻[9]的研究結果相符合,但是從實際使用情況來看,具有第四種結構(N.04)的陀螺誤差最小。導致這一矛盾的原因可能是實際應用中所測的誤差除了溫度梯度引起的誤差外,還包含了結構熱應力引起的誤差。需要進一步研究熱應力對Shupe誤差的影響,將兩者結合起來分析承環結構對光纖環溫度性能的影響。
5 結論
本文利用有限元法對四個不同承環結構的光纖陀螺進行Shupe誤差定量分析,結合溫度實驗結果,驗證了陀螺有限元模型的正確性。對比分析了光纖環由承環結構形式決定的軸向溫度梯度和徑向溫度梯度對Shupe誤差的影響,結果表明:四極對稱繞法繞制的光纖環對軸向溫度梯度更敏感,軸向溫度梯度越大,誤差越大。采用軸向交叉排列的光纖環繞法,如免交叉繞法和螺旋盤式繞法可以減小光纖環的Shupe誤差。設計承環結構時,保證軸向溫度分布均勻且對稱,有助于減小Shupe誤差。
[1] 宋凝芳,關月明,賈明.光纖陀螺光纖環Shupe誤差的多參數影響仿真分析[J].北京航空航天大學學報,2011,37(5):569-573. SONG Ning-fang,GUAN Yue-ming,JIA Ming.Analysis of multi-parameters effect on shupe error in fiber optic gyroscope fiber coil[J].Journal of Beihang University,2011,37(5):569-573.
[2] D.M.Shupe.Thermally induced non-reciprocity in the fiber optic interferometer[J].Applied Optics,1980,19 (5):654-655.
[3] C.M.Lofts,P.B.Ruffin,M.Parker,C.C.Sung.Investigation of the effects of temporal thermal gradients in fiber optic gyroscope sensing coils[J].Optical Engineering, 1995,34(10):2856-2863.
[4] J.Sawyer,P.B.Ruffin,C.C.Sung.Investigation of the effects of temporal thermal gradients in fiber optic gyroscope sensing coils(part 2)[J].Optical Engineering,1997,36 (1):29-34.
[5] Mohr F,Schadt F.Bias error in fiber optic gyroscopes due to elasto-optic interactions in the sensor fiber[C].Proceedings of SPIE-The International Society for Optical Engineering,2004,5502:410-413.
[6] MohrF, SchadtF.Rigoroustreatmentoffiberenvironmental interactions in fiber gyroscopes[C].IEEE Region 8 International Conference on Computational Technologies in Electrical and Electronics Engineering,2008,Sibircon,IEEE,2008:372-375.
[7] Mohr F.Thermooptically induced bias drift in fiber optical Sagnacinterferometers[J].JournalofLightwave Technology,1996,14(1):27-41.
[8] 楊世銘,陶文銓.傳熱學[M].北京:高等教育出版社,2006. YANGShi-ming,TAOWen-quan.Heattransmission science[M].Beijing:Higher Education Press,2006.
[9] 關月明.螺旋盤式光纖環繞制的關鍵技術研究[D].北京航空航天大學,2010. GUAN Yue-ming.Study on key technology of the spiral disc fiber winding method[D].Beihang University,2010.
Effects of Temporal Thermal Gradient on the Shupe Error of Fiber Coil
LIU Guo-jun,ZHANG Bo,PAN Xiong
(School of Instrumentation Science and Optoelectronics Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191)
Optomechanical structure of fiber optic gyro(FOG)may affect thermal gradients distribution of fiber coil,which influence the precision of fog.Finite element models of four FOGs with different kinds of configurations were set up and temporal thermal simulation was done,through which we got the temperature distribution of fiber optic rings.According to digital discrete model of fiber ring cross section,the temperature curves along the fiber length were plotted.Then we computed the Shupe errors caused by radial thermal gradient(RTG)and axial thermal gradient(ATG).The results show that different kinds of optomechanical structures affect the ATG and RTG,the former has greater influence on the Shupe error of the quadrupoar winding fiber coil.
fiber coil;optomechanical structure;radial thermal gradient(RTG);axial thermal gradient(ATG);shupe error
V241.5
A
1674-5558(2016)03-01124
10.3969/j.issn.1674-5558.2016.03.012
2015-05-21
劉國軍,男,碩士,研究方向為光纖陀螺技術。

