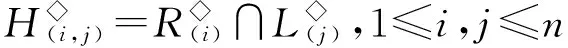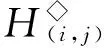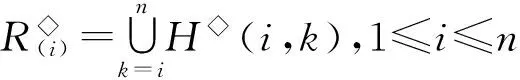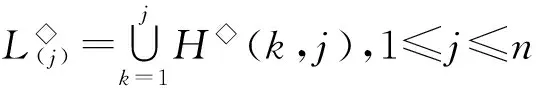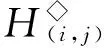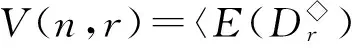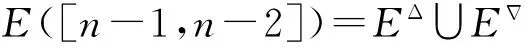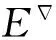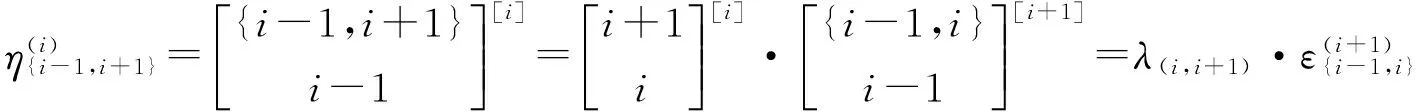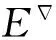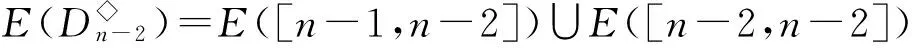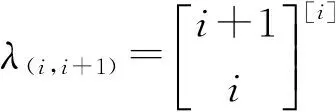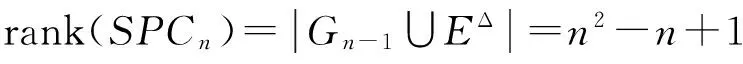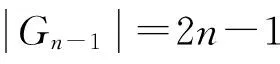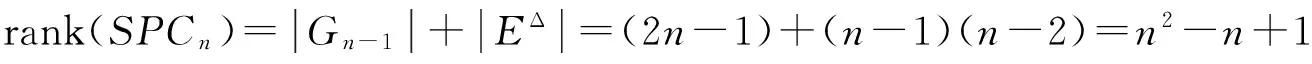半群SPCn的秩

田應信，游泰杰，趙　平

(1.銅仁職業技術學院信息工程學院，貴州 銅仁 554300；2.貴州師范大學數學科學學院，貴州 貴陽 550001)

?

半群SPCn的秩

田應信1，游泰杰2，趙平2

(1.銅仁職業技術學院信息工程學院，貴州 銅仁 554300；2.貴州師范大學數學科學學院，貴州 貴陽 550001)

設[n]={1，2，…，n}是正自然數集，Cn和PCn分別為[n]上的保序且降序變換半群和保序且降序部分變換半群. 記SPCn=PCnCn.對n≥5， 證明了半群SPCn的秩為n2-n+1.

變換半群；降序；保序；秩

1　預備知識

設[n]={1，2，…，n}， 并賦予自然序，Singn和Pn是分別為[n]上的奇異變換半群和部分變換半群.設α∈Pn，若對任意x，y∈dom(α)，x≤y?xα≤yα， 則稱α是保序的. 設POn為Pn中的所有保序部分變換之集(不含[n]上的恒等變換)，則POn是Pn的子半群，稱POn為[n]上的保序部分變換半群.設PCn={α∈POn|?x∈dom(α)，xα≤x}，則PCn是POn的子半群，稱PCn為[n]上降序且保序部分變換半群.記On=POn∩Singn，Cn=PCn∩Singn，則On和Cn都是POn的子半群，稱On和Cn分別為保序變換半群和保序且降序變換半群.記SPOn=POnOn，SPCn=PCnCn，則SPOn和SPCn都是POn的子半群，稱SPOn和SPCn分別為保序嚴格部分變換半群和降序且保序嚴格部分變換半群.

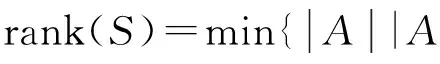
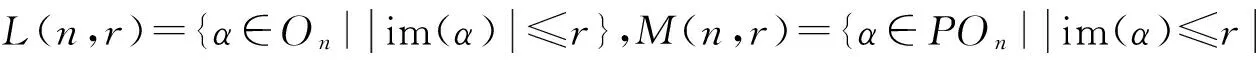
設S是V(n，r)的子集. 通常，用E(S)表示S中所有冪等元組成的集合.

2　主要結論及證明

為敘述方便，文獻[6]在V(n，r)上引入二元關系：對任意的α，β∈V(n，r)，定義

(α，β)∈L◇?im(α)=im(β)；

(α，β)∈R◇?dom(α)=dom(β)；

則L◇，R◇和D◇都是V(n，r)上的等價關系，易見L◇∈D◇，R◇∈D◇.對0≤k≤r≤n-1，記

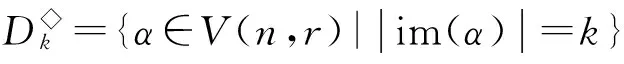
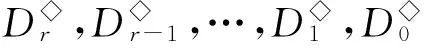
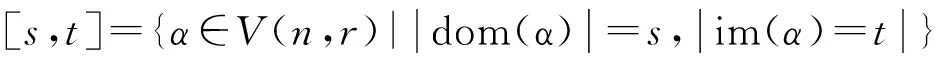
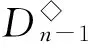
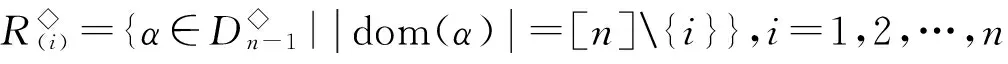
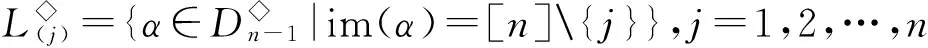
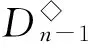
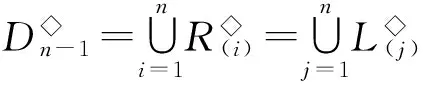
設A，B是[n]的非空子集.若對任意a∈A，b∈B，有a

其中a1

設

引理2.1設1≤i

引理2.2設n≥5，則[n-1，n-1]?〈Gn-1〉.

證明注意到

任取α∈[n-1，n-1]，存在1≤i≤j≤n，使得α=λ(i，j).若i=j，則α=λ(i，i)∈H◇(i，i)?Gn-1?〈Gn-1〉.注意到H◇(i，i+1)={λ(i，i+1)}且H◇(i，i+1)?Gn-1，若i

λ(i，i+1)λ(i+1，i+2)…λ(j-1，j)=λ(i，j)=α，

從而α∈〈Gn-1〉.再由α的任意性可得[n-1，n-1]?〈Gn-1〉.

引理2.3設n≥5，則E([n-2，n-2])?〈E([n-1，n-1])〉.

證明設δi，j(i≠j)是[n]{i，j}上的恒等映射，則由半群SPCn的保序性可知

任取α∈E([n-2，n-2])，則存在i≠j使得α=δi，j. 注意到λ(i，i)，λ(j，j)∈E([n-1，n-1])(由注2.1可知)，易驗證δi，j=λ(i，i)λ(j，j)，從而α=δi，j∈〈E([n-1，n-1])〉. 由α的任意性可得E([n-2，n-2])?〈E([n-1，n-1])〉.

證明類似文獻[6]中的定理2的證明過程.

dom(α)=[n]{k}，Aiα=ai，1≤i≤r，1≤k≤r;

xα=x，x∈dom(α)(A1∪A2∪…∪Ar).

考慮[n-1，n-2]中的冪等元. 由半群SPCn的保序且降序性可知[n-1，n-2]中的冪等元有如下形式：

令：

引理2.6設n≥5，則SPCn?〈Gn-1∪EΔ〉.

引理2.7設G是半群SPCn的生成集，則對任意1≤i≤n，有λ(i，i)∈G.

證明由G是半群SPCn的生成集可知存在α1，α2，…，αr∈G， 使λ(i，i)=α1α2…αr，再由λ(i，i)∈[n-1，n-1]可得dom(α1)=dom(λ(i，i))=[n]{i}.我們斷言α1=λ(i，i).(ⅰ)若r=1，則α1=λ(i，i).(ⅱ)若r≥2，則顯然α2…αr∈SPCn. 注意到λ(i，i)是[n]{i}的恒等變換(由注2.1可知)且α1∈SPCn，若α1≠λ(i，i)，則存在x∈[n]{i}，使xα1

綜上所述，α1=λ(i，i). 因此λ(i，i)=α1∈G.

引理2.8設G是半群SPCn的生成集，則對任意1≤i≤n-1，有λ(i，i+1)∈G.

x=xλ(i，i+1)=(xα1α2…αr-1)αr≤(xα1α2…αr-2)αr-1≤…≤(xα1)α2≤xα1≤x，x∈Di，i+1，

從而

xα1α2…αr-1αr=xα1α2…αr-1=…=xα1α2=xα1=x，x∈Di，i+1.

(1)

我們斷言：對1≤m≤r，有

xαm=x，x∈Di，i+1.

(2)

事實上，若m=1，則由(1)式可得xα1=x，x∈Di，i+1.若2≤m≤r，則由(1)式，

xα1α2…αm-1=xα1α2…αm-1αm=x，x∈Di，i+1，

從而

xαm=(xα1…αm-1)αm=x，x∈Di，i+1.

im(αk)=dom(αk+1)，1≤k≤r-1.

(3)

引理2.9設G是半群SPCn的生成集，則Gn-1?G.

證明注意到

由引理2.7—2.8，Gn-1?G.

引理2.10設G是半群SPCn的生成集，則EΔ?G.

由G是半群SPCn的生成集可知存在α1，α2，…，αs∈G，使ε=α1α2…αs.(ⅰ)若s=1，則ε=α1∈G.(ⅱ)若s≥2，則由ε=α1α2…αm∈SPCn(1≤m≤s)可得

x=xε=(xα1α2…αs-1)αs≤(xα1α2…αs-2)αs-1≤…≤(xα1)α2≤xα1≤x，x∈Dk，i+1，

從而

xα1α2…αs-1αs=xα1α2…αs-2αs-1=…=xα1α2=xα1=x，x∈Dk，i+1.

(4)

我們斷言：對1≤m≤s，有

xαm=x，x∈Dk，i+1.

(5)

若m=1，由(4)式可得xα1=x，x∈Dk，i+1.若2≤m≤s，由(4)式可得

xα1α2…αm-1=xα1α2…αm-1αm=x，x∈Dk，i+1，

從而

xαm=(xα1α2…αm-1)αm=x，x∈Dk，i+1，

故(5)式得證. 從而易得

Dk，i+1?dom(αm)，1≤m≤s.

(6)

i=(i+1)ε=(i+1)α1α2…αs=(i+1)α2…αs，

i=(i+1)ε=(i+1)α1α2…αs=(i+1)α2…αs=(i+1)α3…αs，

重復上述過程可得

再由(6)式，α1=α2=…=αs且它們都為Dk，i+1∪{i+1}上的恒等變換，從而

[1]GOMES M S，HOWIE J M. On the ranks of certain semigroups of order-preserving transformation semigroup[J]. Semigroup Forum，1992，45(1):271-282.

[2]GARBA G U. On the idempotent ranks of certain semigroups of order-preserving transformation semigroup[J]. Portugal Math，1994(51):185-204.

[3]HIGGINS P M. Idempotent depth in semigroups of order-preservin mappings[J].Proc Roy Soc Edinburgh Sec A，1994，124(5):1045-1058.

[4]趙平，游泰杰，徐波. 降序且保序有限部分變換半群的冪等元的秩[J].山東大學學報(理學版)，2011，46(4):75-77.

[5]LARADJI A，UMAR A. On certain finite semigroups of orderdecreasing trans formations[J].Semigroup Forum，2004，69:184-200.

[6]吳江燕，游泰杰. 保序部分變換半群POn的平方冪等元[J]. 東北師大學報(自然科學版)，2015，47(1)：6-11.

[7]趙平. 半群V(n，r)的冪等元秩[J]. 山東大學學報(理學版)，2012，47(2):78-81.

(責任編輯：李亞軍)

On the rank of the semigroupSPCn

TIAN Ying-xin1，YOU Tai-jie2，ZHAO Ping2

(1.School of Information Engineering，Tongren Polytechnic college，Tongren 554300， China；2.School of Mathematics and Computer Science，Guizhou Normal University，Guiyang 550001，China)

Let[n]={1，2，…，n} be a natural order set，CnandPCnbe the semigroups consisting of order-preserving or order-decreasing transformations and partial order-preserving or order-decreasing transformations on [n]，respectively. DenoteSPCn=PCnCn，it is called the order-preserving and order-decreasing stricty partial transformations semigroups. Forn≥5， it is given that the rank of the semigroupSPCnisn2-n+1.

transformation semigroup； order-decreasing； order-preserving;rank

1000-1832(2016)03-0009-05

2015-02-04

國家自然科學基金資助項目(11461014)；貴州省自然科學基金資助項目(黔科合J字[2013]2225號).

田應信(1990—)，女，碩士，主要從事半群代數理論研究；通信作者：游泰杰(1959—)，男，教授，主要從事半群代數理論研究；趙平(1973—)，男，教授，主要從事半群代數理論研究.

O 152.7[學科代碼]110·2115

A

[DOI]10.16163/j.cnki.22-1123/n.2016.03.003