星載BDS/GPS低軌衛星自主定軌精度分析

熊　超，賈小林，朱　俊，盧傳芳

(1.西安航天天繪數據技術有限公司，陜西　西安　710100；2.地理信息工程國家重點實驗室，陜西　西安　710054；3.西安測繪研究所，陜西　西安　710054；4.宇航動力學國家重點實驗室，陜西　西安　710043；5.中國西安衛星測控中心，陜西　西安　710043)

?

星載BDS/GPS低軌衛星自主定軌精度分析

熊超1，賈小林2，3，朱俊4，5，盧傳芳1

(1.西安航天天繪數據技術有限公司，陜西西安710100；2.地理信息工程國家重點實驗室，陜西西安710054；3.西安測繪研究所，陜西西安710054；4.宇航動力學國家重點實驗室，陜西西安710043；5.中國西安衛星測控中心，陜西西安710043)

為了進一步研究低軌衛星搭載BDS/GPS接收機實現自主定軌的熱點問題，討論了基于星載BDS/GPS自主定軌需要考慮的數學模型，提出了顧及動力學模型的Helmert方差分量估計實現基于星載BDS/GPS自主定軌的方法，并闡述了方法的原理及自主定軌的過程；然后基于自主研發程序，利用高動態信號仿真器仿真的星載BDS/GPS數據驗證了基于星載BDS/GPS自主定軌的可行性及其能達到的精度。結果表明，顧及動力學模型的Helmert方差分量估計既可以較好地解決BDS/GPS觀測值的合理定權問題，又可以有效地減弱粗差的影響，提高定軌精度。

自主定軌；擴展卡爾曼濾波；方差分量估計

0　引言

北斗衛星導航系統(BeiDou navigation satellite system，BDS)是我國自主研發、獨立運行的全球衛星導航系統。其空間星座由5條地球靜止軌道(geostationary Earth orbit，GEO)衛星、27條中圓地球軌道(medium Earth orbit，MEO)衛星和3條傾斜地球同步軌道(inclined geosynchronous satellite orbit，IGSO)衛星組成。截止到2012年底，在軌工作衛星有5顆GEO衛星、4顆MEO衛星和5顆IGSO衛星共計14顆衛星，已具備區域服務能力[1]。

長期以來，基于衛星導航系統的低軌衛星高精度定軌主要依靠全球定位系統(global positioning system，GPS)，圍繞各種不同需求，低軌衛星的星載GPS定軌技術取得了迅速發展。首次用星載GPS測量獲得cm級定軌精度的成功范例是TOPEX/POSEIDON海洋測高衛星(簡稱為T/P衛星)。美國航空航天局(National Aeronautics and Space Administration，NASA)下屬的噴氣推進實驗室(Jet Propulsion Laboratory，JPL)用星載GPS測量數據作精密定軌數據處理，結果表明：T/P衛星徑向軌道精度達到3 cm，切向和法向的軌道精度優于10 cm。星載GPS測量在衛星精密定軌方面取得巨大成功的同時，世界各國也在積極開展自主定軌的研究和試驗工作。JPL在其研制的高精度定位定軌軟件GIPSY的基礎上，研制出一套實時版GIPSY軟件(real-time GIPSY，RTG)[2]。該軟件不僅可用于低軌衛星的自主定軌，也可用于地面飛機的實時定位。用T/P衛星實測數據驗證表明，在有選擇可用性(selective availability，SA) 的影響下，經過約4 h的濾波收斂時間后，3維數據求得的實時定軌軌道均方根(root mean square，RMS)為3～5 m。文獻[3]將RTG軟件用于SAC-C衛星的自主定軌，結果表明：自主定軌精度可達到1.5 m。文獻[4]于2006年研制成功了星載GPS自主定軌軟件SATODS，并用大量的星載GPS實測數據進行模擬自主定軌的試驗，試驗結果表明：自主定軌精度可以達到±1.5～3.0 m軌道精度和±3 mm/s的速度精度[4]。

低軌衛星及星座作為高精度對地觀測系統的傳感器搭載平臺，已廣泛應用于資源遙感、大氣探測、海洋開發、軍事偵察等領域，在科學研究、經濟建設、社會發展及國家安全中具有不可替代的作用。作為我國新一代自主導航系統，BDS區域導航系統的建成將改變我國對GPS依賴的局面提供可能；同時BDS/GPS組合衛星導航系統可以使可視衛星數顯著增加，并改善衛星的幾何分布結構，提高系統的可用性和可靠性[1]；因此低軌衛星搭載BDS/GPS接收機實現自主定軌將成為定軌領域的熱點問題。

本文研究討論基于星載BDS/GPS自主定軌相關問題，并實驗驗證基于星載BDS/GPS自主定軌的可行性及其能達到的精度。

1　數據處理策略

1.1數據處理

1.1.1狀態方程和觀測方程

星載BDS/GPS自主定軌是根據帶有隨機誤差的一系列觀測信息和衛星軌道的動力學信息，依照一定的準則，對衛星運行狀態參數、動力學模型參數、觀測模型參數等進行最優估計的過程。自主定軌常以序貫或者遞推方式進行數據處理和參數估計，一般采用擴展卡爾曼濾波(extended Kalman filter，EKF)估計方法[4-5]。建立星載BDS和GPS自主定軌的數學模型，必須建立自主定軌擴展卡爾曼濾波的狀態方程和觀測方程。

對于低軌衛星來說，大氣阻力和太陽光壓這2種非保守力對衛星軌道影響較大，同時又是難以精確模型化的攝動力，在動力學定軌時常將大氣阻力系數CD和太陽光壓系數CR作為狀態參數進行估計[6-8]。相比于單一導航衛星系統，由于不同導航系統間信號延遲的存在，在觀測方程中需顧及BDS/GPS系統間信號延遲，一般采用GPS接收機鐘差作為基準，將BDS接收機鐘差表達成GPS接收機鐘差的形式。因此自主定軌系統狀態向量確定為

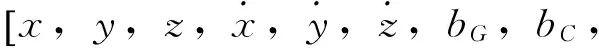
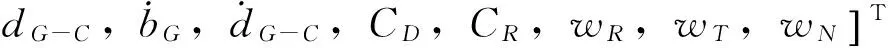
(1)

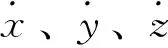
采用消電離層偽距非差線性組合PC觀測值，同時顧及BDS/GPS的系統時間偏差δtG-C，其觀測方程可表示為：

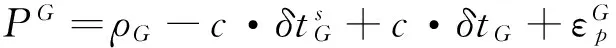
(2)

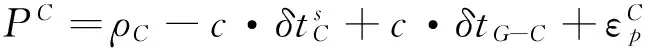
(3)

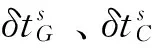
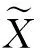
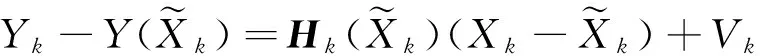
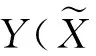
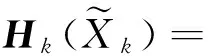
(5)

對于BDS衛星可表示為

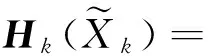
(6)

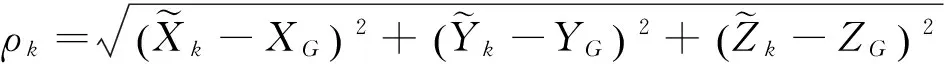
1.1.2觀測模型和動力學模型

本文在自主定軌時，處理的是消電離層偽距非差線性組合PC觀測值。表1給出了具體的觀測模型。

對于低軌衛星來說，大氣阻力和太陽光壓這2種非保守力對衛星軌道影響較大，同時又是難以精確模型化的攝動力。在動力學定軌時常將大氣阻力系數和太陽光壓系數作為狀態參數進行估計。詳細的動力學模型見表2。

表1　觀測模型和估計參數

表2　動力學模型和估計參數

1.2定權策略

由于BDS星座的分布、頻率特征、軌道精度、觀測數據質量等方面和GPS等都存在差別，如何對觀測資料進行合理加權是星載BDS和GPS自主定軌中的一個重要問題。在實際定軌過程中，觀測資料有3種途徑定權：1)利用觀測文件中提供的標準偏差；2)根據經驗定權；3)利用方差分量估計。由于觀測數據文件中觀測值的標準偏差只代表觀測的內符合情況，而經驗加權法也不能很好地反映觀測資料的實際精度，低軌衛星不斷運動造成隨機噪聲改變進而影響固定權比，會導致自主定軌精度下降。Helmert方差分量估計是一種通過迭代計算自適應確定不同類觀測值權比的驗后方差分量估計方法，能夠在計算過程中自動地調整不同類觀測值的權比，合理分配不同類觀測值對整個解的貢獻大小；因而在數據處理領域得到了廣泛的應用。數據處理過程中，觀測信息難免有粗差以及軌道預報值難免有異常，為減弱粗差和軌道預報值異常對自主定軌結果的影響，采用顧及動力學模型的Helmert方差分量估計方法[9]對仿真數據進行星載BDS/GPS自主定軌實驗。

首先可構造極值條件為

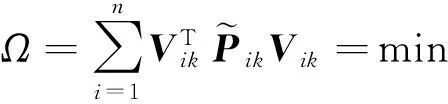
(7)

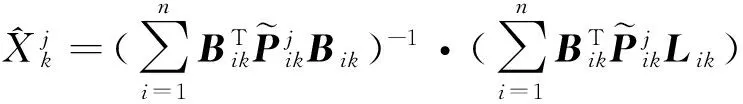
(8)

然后顧及動力學模型信息，采用自適應估計原理[10]，其原理為

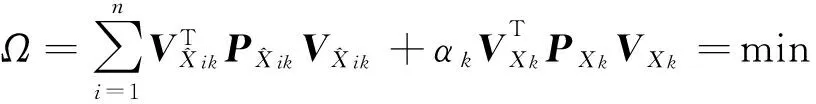
(9)

則自適應融合解為：

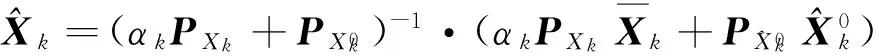
(10)

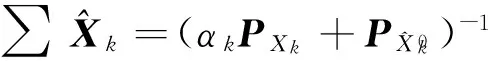
(11)

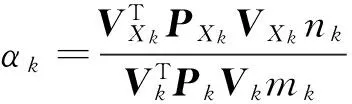
(12)

2　實驗與結果分析

2.1數據準備及處理流程

目前尚無法獲取星載BDS/GPS接收機實測數據，本文通過模擬數據來進行試驗，試驗數據是由高動態信號仿真器產生。高動態信號仿真器根據BDS和GPS衛星的精密軌道和鐘差以及在軌衛星的運動軌跡，模擬產生射頻信號。接收機通過接收模擬射頻信號獲取各衛星的觀測值。

自主定軌仿真驗證軟件通過解算接收機的觀測值得到自主定軌結果，定軌結果與仿真器輸出的衛星軌道比較可以綜合分析利用低軌衛星高動態BDS/GPS接收機的自主定軌能力。圖1是星載BDS/GPS自主定軌仿真驗證的流程圖。

本文使用的試驗數據為：2014-09-05的BDS精密星歷和鐘差、2014-09-05的GPS精密星歷和鐘差。數據來源為由地球科學研究中心(DeutschesGeoForschungsZentrum，GFZ)提供的BDS和GPS雙系統的軌道鐘差產品，文件名為gbm18085.sp3和gbm18085.clk。廣播星歷采用包含BDS和GPS的多系統混合的廣播星歷產品，文件名為brdm2480.14p。觀測數據采用由高動態信號仿真器生成的2014-09-05的BDS/GPS仿真觀測數據。

本文以重力反演與氣候實驗衛星(gravityrecoveryandclimateexperiment，GRACE)為背景模擬1顆具有星載BDS/GPS接收機的低軌衛星GRACE-A。GRACE-A軌道真值取JPL提供的GRACE-A精密軌道。本文采用2014-09-05全天24h的星載BDS/GPS模擬觀測數據進行數據處理。

2.2不同定權策略的自主定軌精度分析

由于BDS與GPS的衛星星歷精度不同，觀測數據噪聲也不同，為分析這些不同對BDS/GPS自主定軌結果的影響，在試驗中分別對BDS和GPS進行不同定權策略的自主定軌。經驗定權采用BDS和GPS按照1:3的權比來定權。采用2014-09-05的BDS/GPS仿真觀測數據采用不同定權策略進行BDS/GPS自主定軌精度分析。

采用上述仿真數據，按照以下方案進行數據處理，測試不同定權策略的聯合自主定軌的精度及其性能。數據處理方案包括：1)方案1，經驗定權的自主定軌的精度分析；2)方案2，Helmert方差分量估計的自主定軌的精度分析；3)方案3，顧及動力學模型的Helmert方差分量估計的自主定軌的精度分析。不同策略的定軌結果如圖2所示。

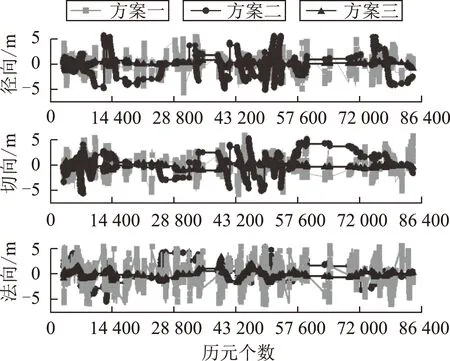
圖2　不同定權策略BDS/GPS自主定軌結果

方案1和方案2不考慮動力學模型。從圖2可以看出，采用經驗定權方法進行自主定軌波動較大，徑向、切向和法向方向均呈現明顯的“尖刺”狀。采用Helmert方差分量估計后，誤差曲線較之經驗定權平緩些，這是因為Helmert方差分量估計合理調整了BDS和GPS觀測信息的權比，保證了BDS和GPS觀測信息在聯合自主定軌中的合理貢獻；但從圖2中可以看出，誤差曲線仍然存在部分“尖刺”狀。對于星載高動態觀測數據來說，觀測信息存在粗差不可避免，存在部分異常觀測數據，導致估計的方差分量不可靠。而采用顧及動力學模型的Helmert方差分量估計，誤差曲線比采用Helmert方差分量估計的誤差曲線更為平緩；不僅合理地分配了BDS和GPS觀測信息在自主定軌中的貢獻，而且自適應地合理利用了動力學模型信息，聯合自主定軌結果誤差曲線平穩。

為了進一步分析不同定權策略對BDS/GPS聯合自主定軌結果的影響，我們對3種方案進行了位置和速度的徑向、切向、法向和3維定軌結果的RMS統計，具體詳見表3和表4。

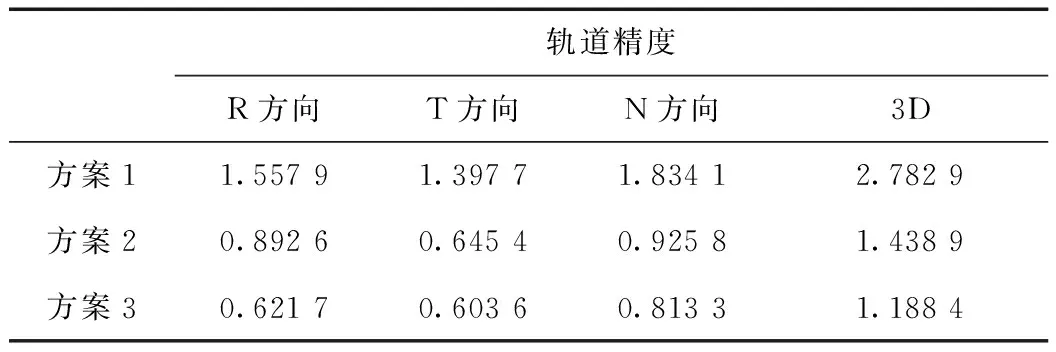
表3　不同定權策略BDS/GPS自主定軌位置結果　m

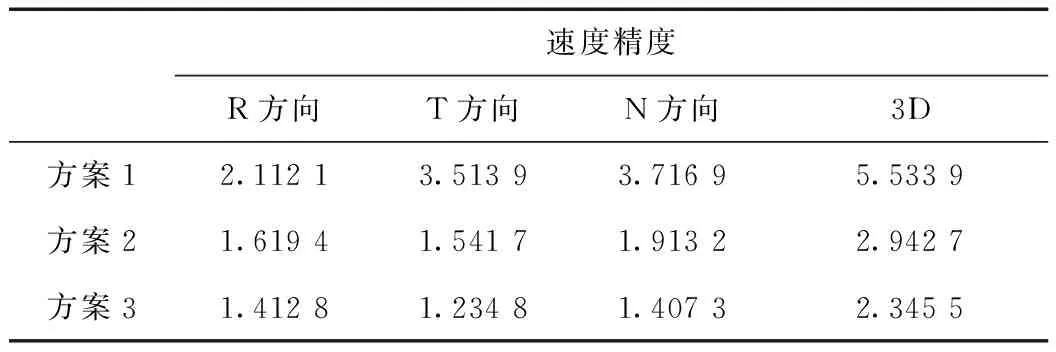
表4　不同定權策略BDS/GPS自主定軌速度結果　mm·s-1

從表3和表4的位置和速度結果表明：Helmert方差分量估計自主定軌位置結果比經驗定權法在徑向、切向、法向和3維方向提高了0.66、0.75、0.91和1.34 m；顧及動力學模型的Helmert方差分量估計自主定軌位置結果比Helmert方差分量估計自主定軌結果各方向分別提高了0.27、0.04、0.11和0.25 m；對于速度結果來說，Helmert方差分量估計和顧及動力學模型的Helmert方差分量估計相比經驗定權法在切向、法向方向改善較大，主要是因為BDS衛星目前主要分布在亞太地區，部分區域觀測信息質量較差，采用方差分量估計方法可以提高GPS觀測信息在聯合自主定軌的貢獻；顧及動力學模型的Helmert方差分量估計自主定軌位置3維RMS為1.188 m，速度3維RMS為2.345 mm/s。表3和表4表明顧及動力學模型的Helmert方差分量估計既較好地解決了BDS/GPS觀測值的合理定權問題，又有效地減弱了粗差的影響，從而提高了定軌精度。

2.3BDS、GPS和BDS/GPS自主定軌精度分析

BDS的區域系統空間部分由5顆GEO衛星、5顆IGSO衛星和4顆MEO衛星星座構成，其中5顆GEO衛星分別定點于58.75°E、80°E、110.5°E、140°E、160°E；5顆IGSO衛星分布于3個軌道面上，其中I1、I2和I3星下點軌跡重合，交點地理經度處于118°E，I5和I6分別和I1、I2處于同一軌道面，與I1、I2各自相差23°，交點地理經度處于95°E；4顆MEO衛星軌道高度21 528 km，為7 d 13圈回歸，4顆衛星分別位于WALKER24/3/1星座的第一和第二軌道面上，星下點軌跡見圖3。

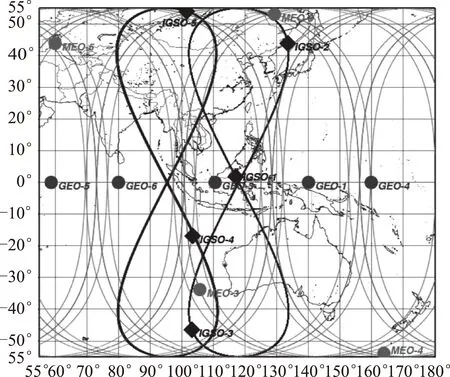
圖3　BDS區域衛星導航系統(5GEO/5IGSO/4MEO)星下點軌跡

為了評價BDS/GPS聯合自主定軌的性能，通常可以將BDS/GPS聯合自主定軌的結果與BDS、GPS自主定軌的結果進行比較分析。采用2014-09-05的BDS/GPS仿真觀測數據進行GPS、BDS和BDS/GPS自主定軌精度分析。

采用上述仿真數據，按照以下方案進行數據處理，測試聯合自主定軌的精度及其性能。數據處理方案包括：1)方案1，GPS自主定軌的精度分析；2)方案2，BD2自主定軌的精度分析；3)方案3，GPS/BD2聯合自主定軌的精度分析。

統計試驗數據的可見衛星數如圖4所示。GPS可見衛星數為7～11顆；BDS可見衛星數為3～7顆；BDS和GPS聯合可見衛星數為12～16顆。加入BDS后歷元可見衛星數增加了5顆左右。

圖5為試驗數據BDS、GPS和BDS/GPS的位置精度衰減因子(position dilution of precision，PDOP)值統計圖。

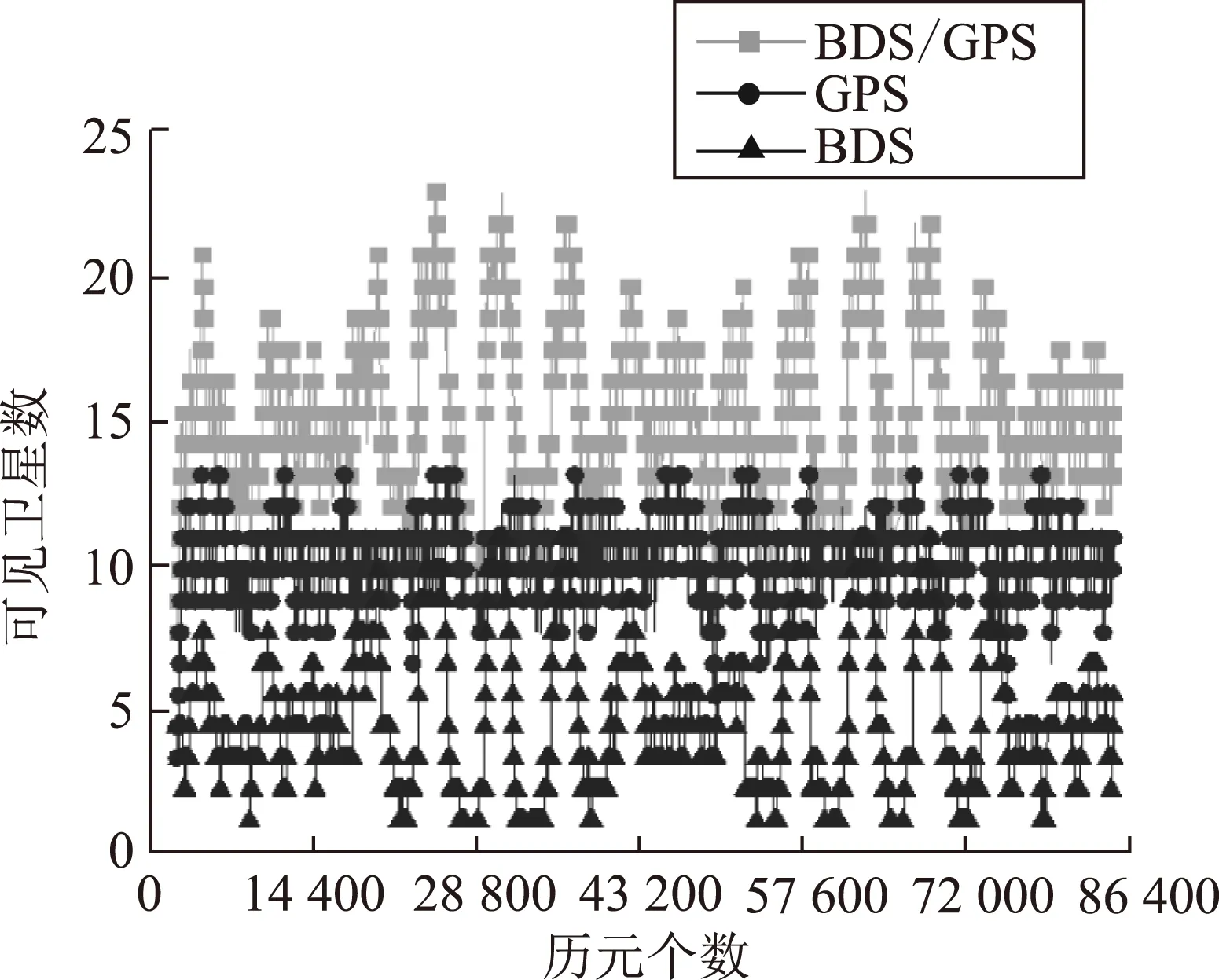
圖4　可見衛星數

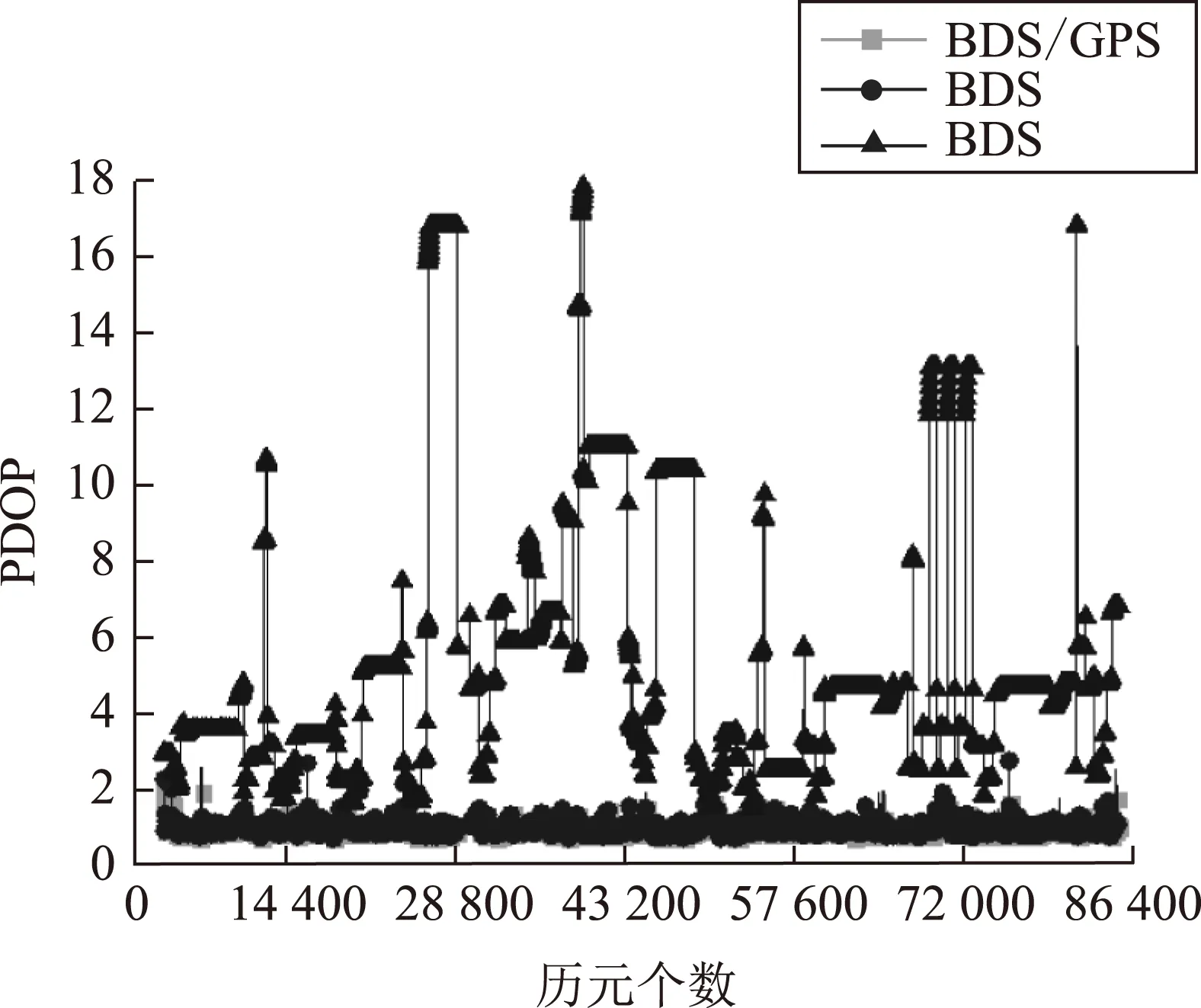
圖5　PDOP統計

由圖5可以看出，GPS和BDS/GPS的PDOP值相差很小，均值分別為0.87和0.82，GPS加入BDS后，PDOP減小了0.05；而BDS的PDOP值則出現較大波動，均值為4.96，主要是因為BDS為區域系統，衛星主要分布在亞太區域(見圖3)，當低軌衛星運行到覆蓋區域內，可以觀測到多于5顆衛星，幾何分布結構好，當低軌衛星運行到覆蓋區域之外時，幾何分布結構差。

采用星載BDS/GPS試驗數據中的GPS觀測數據進行自主定軌的結果如圖6和圖7所示。

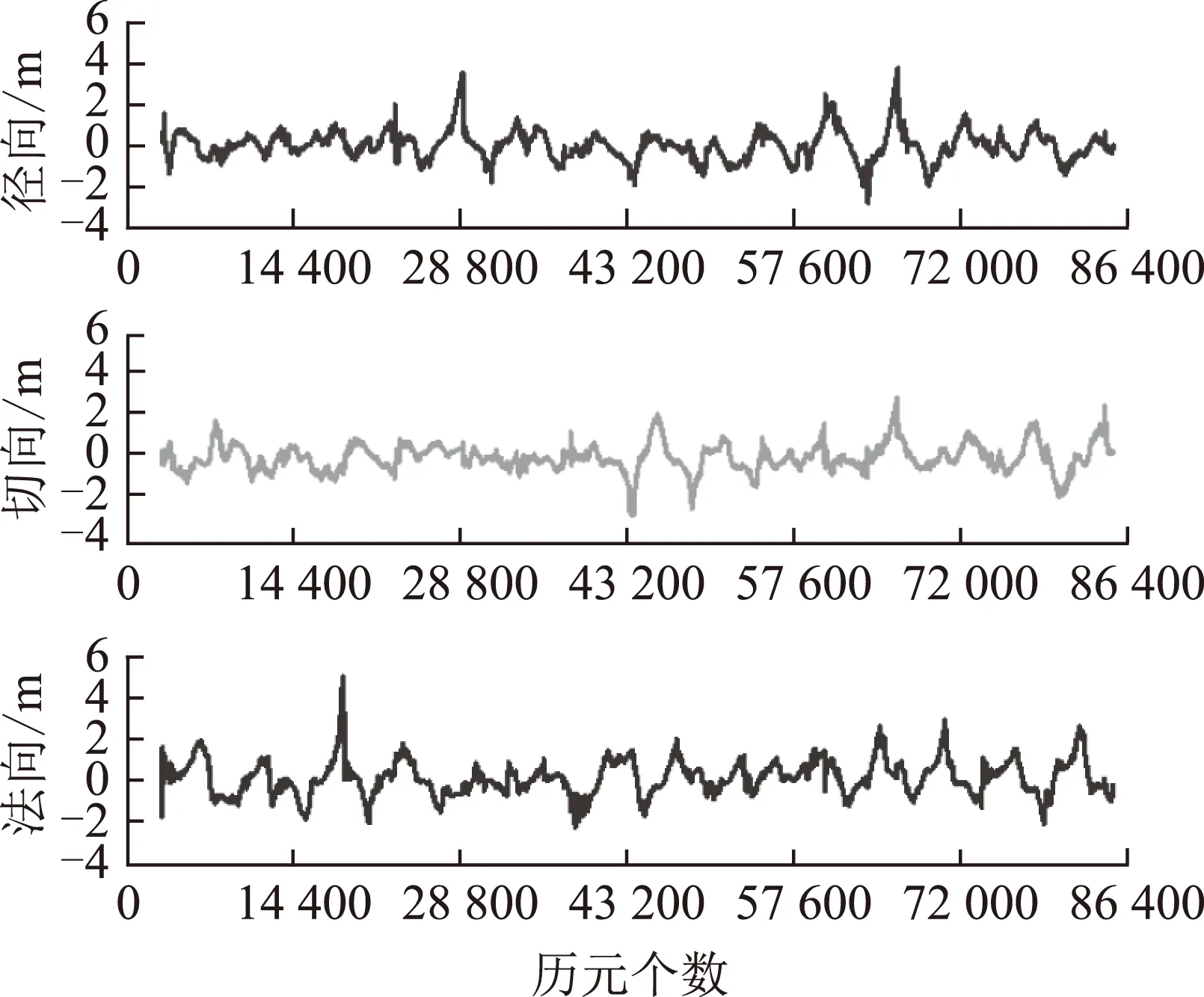
圖6　GPS自主定軌位置誤差

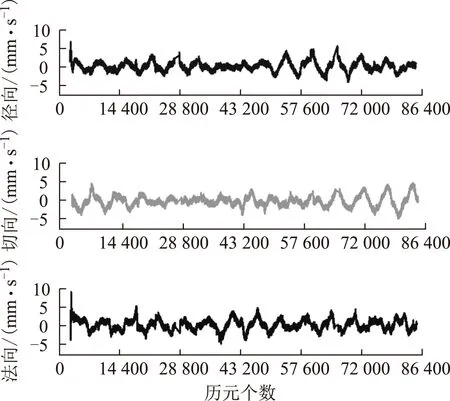
圖7　GPS自主定軌速度誤差

經過統計，僅采用GPS觀測數據進行自主定軌徑向、切向和法向的位置誤差分別為0.64、0.64和0.86 m；3維位置誤差為1.25 m；徑向、切向和法向的速度誤差分別為1.44、1.28和1.44 mm/s；3維速度誤差為2.41 mm/s。

采用星載BDS/GPS試驗數據中的BDS觀測數據進行自主定軌。結果如圖8和圖9所示。

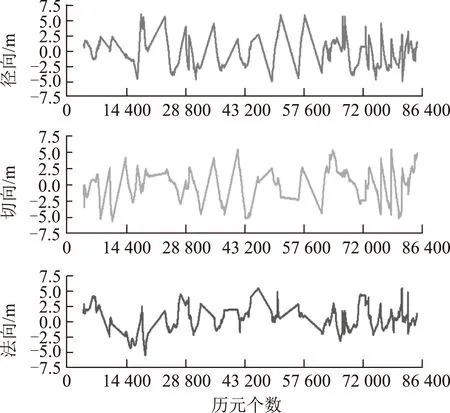
圖8　BDS自主定軌位置誤差

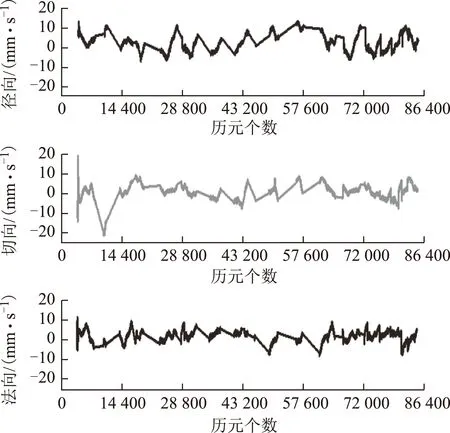
圖9　BDS自主定軌速度誤差

從圖8中可以看出，僅用BDS數據的自主定軌結果的徑向、切向和法向的軌道位置和速度誤差很不穩定，起伏較大。主要是因為BDS為區域系統，主要覆蓋亞太區域，當低軌衛星運行到覆蓋區域內，可以觀測到多于5顆衛星，定軌精度較為穩定；當低軌衛星運行到覆蓋區域之外，觀測衛星數減少，無法進行單點定位，自主定軌處于預報中，軌道精度較差。經過統計，僅用BDS的自主定軌結果徑向軌道誤差在5 m以內，統計RMS值為2.23 m，切向和法向的RMS值分別為2.22和1.99 m；3維位置誤差為3.73 m；徑向、切向和法向的速度誤差分別為3.35、3.68、2.19 mm/s；3維速度誤差為5.44 mm/s。

采用星載BDS/GPS試驗數據進行聯合自主定軌，軌道位置誤差如圖10所示，速度誤差如圖11所示。

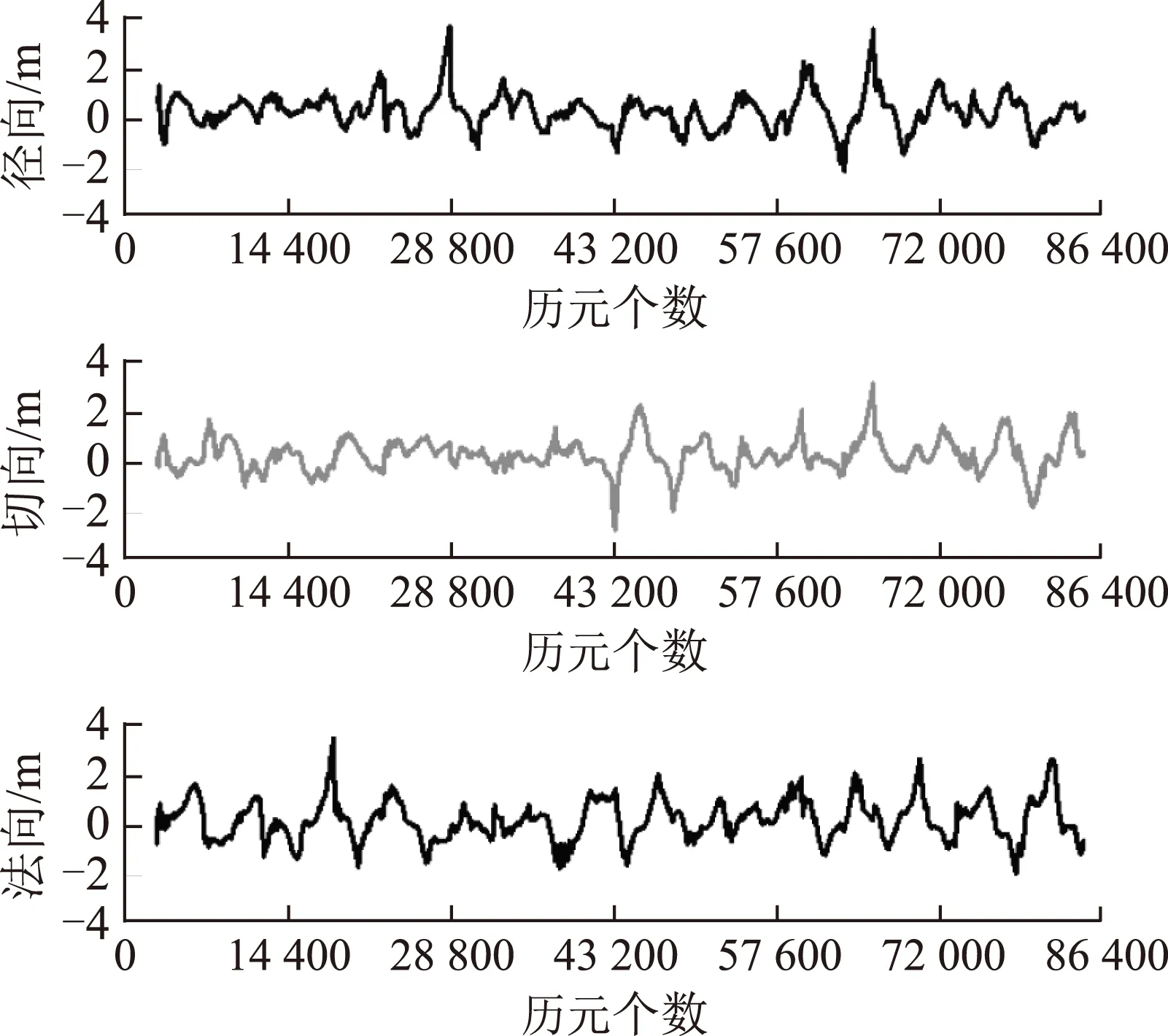
圖10　BDS/GPS自主定軌位置誤差

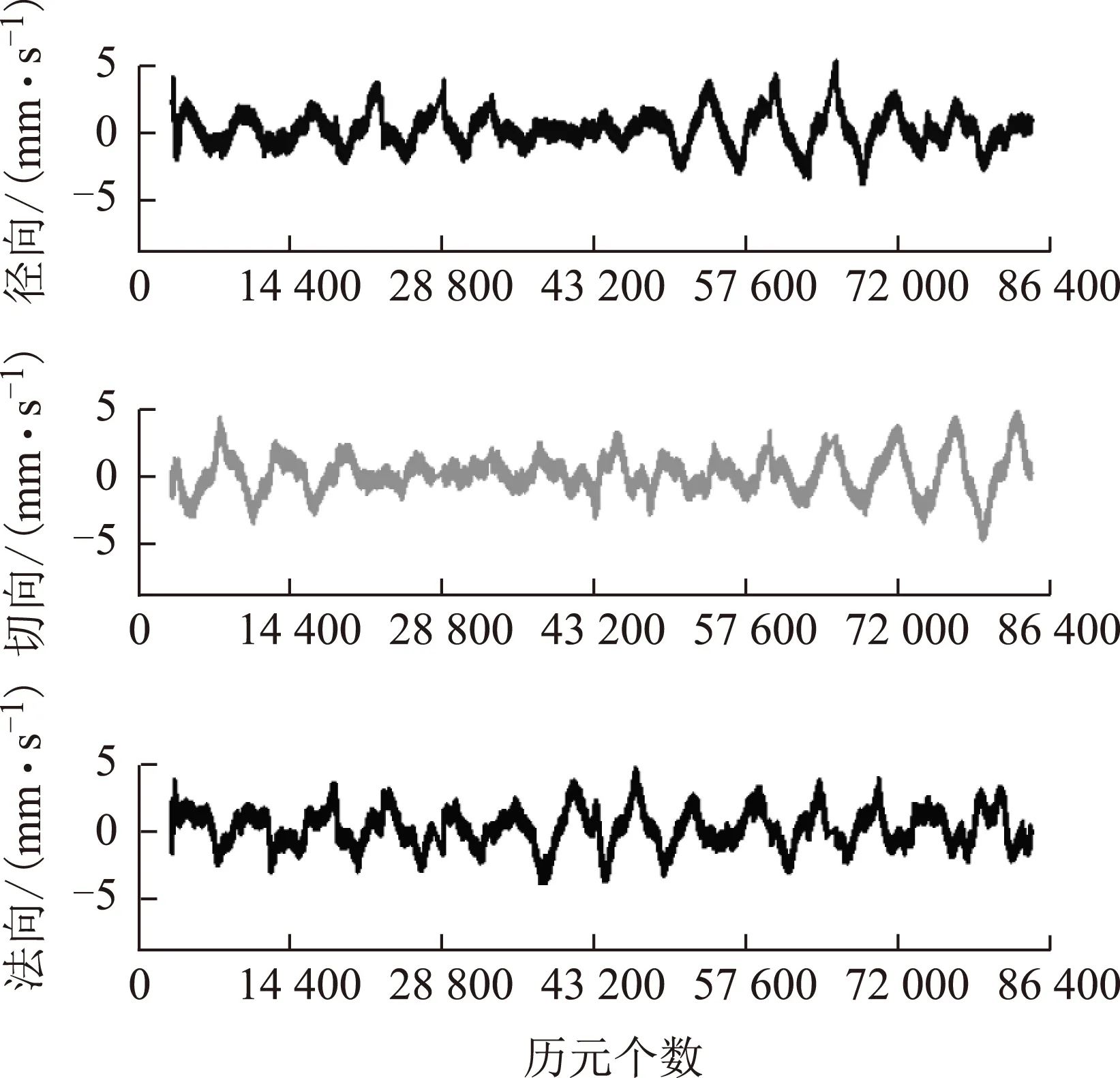
圖11　BDS/GPS自主定軌速度誤差

經過統計，BDS/GPS聯合自主定軌位置誤差徑向、切向和法向分別為0.62、0.60和0.81 m；3維位置誤差為1.19 m；徑向、切向和法向的速度誤差分別為1.41、1.23和1.41 mm/s；3維速度誤差為2.35 mm/s。

統計GPS、BDS和BDS/GPS自主定軌3種方案的位置誤差如表5所示，速度誤差如表6所示。

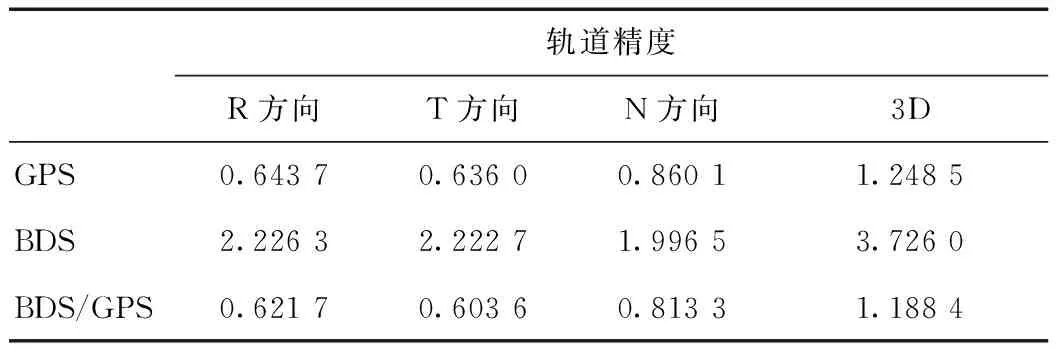
表5　不同方案自主定軌的位置誤差　m

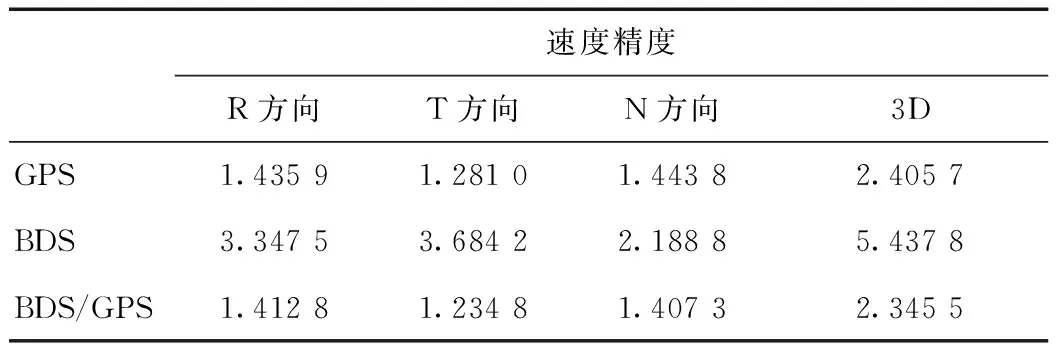
表6　不同方案自主定軌的速度誤差　mm·s-1

將GPS、BDS和BDS/GPS自主定軌3種方案的位置誤差進行統計，結果如圖12所示。

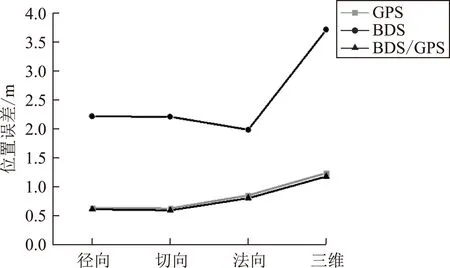
圖12　BDS/GPS自主定軌3種方案的位置誤差

從表5和表6以及圖12中可以看出：僅采用GPS觀測數據的自主定軌和BDS/GPS聯合自主定軌的精度相當；而僅采用BDS觀測數據的自主定軌精度較差。主要是由于GPS衛星星座是全球均勻分布，從圖4可以看出可見衛星數較多而且變化較為平穩，圖5中GPS觀測數據的PDOP均值為0.87與BDS/GPS的PDOP均值0.82相差很小；而BDS為區域系統，從圖3中可以看出BDS的GEO衛星和IGSO衛星主要分布在亞太區域，圖4中顯示BDS可見衛星數變化較大，圖5中顯示BDS的PDOP值波動較大。GPS加入BDS觀測數據后，自主定軌徑向、切向和法向的位置誤差分別提高了3.42%、5.09%和5.44%，3維位置誤差提高了4.81%。GPS信號發生中斷時即僅采用BDS觀測數據進行自主定軌時，3維位置誤差達到3.73 m，可以滿足部分領域軌道位置的應用需求，為改變我國對GPS依賴的局面提供可能。

3　結束語

本文采用高動態信號仿真器生成的星載BDS和GPS仿真數據進行了不同定權策略的BDS/GPS自主定軌精度分析，并進行了BDS、GPS和BDS/GPS自主定軌精度分析，得出以下幾點結論：

1)Helmert方差分量估計和顧及動力學模型的Helmert方差分量估計相比經驗定權法在切向、法向方向改善較大。顧及動力學模型的Helmert方差分量估計既較好地解決了BDS/GPS觀測值的合理定權問題，又有效地減弱了粗差的影響，從而提高了定軌精度。

2)GPS可見衛星數為7～11顆；BDS可見衛星數為3～7顆；BDS和GPS聯合可見衛星數為12～16顆。加入BDS后歷元可見衛星數增加了5顆左右。GPS和BDS/GPS的PDOP值相差很小，均值分別為0.87和0.82，加入BDS后，PDOP減小了0.05；而BDS的PDOP值則出現較大波動，均值為4.96。

3)僅采用GPS觀測數據的自主定軌和BDS/GPS聯合自主定軌的精度相當，加入BDS觀測數據后，BDS/GPS聯合自主定軌徑向、切向和法向的位置誤差分別提高了3.42%、5.09%和5.44%，3維位置誤差提高了4.81%。BDS/GPS聯合自主定軌3維位置誤差為1.19 m，速度誤差為2.35 mm/s。

4)GPS信號發生中斷時即僅采用BDS觀測數據進行自主定軌時，3維位置誤差達到3.73 m，可以滿足部分領域軌道位置的應用需求，為改變我國對GPS依賴的局面提供可能。

隨著我國BDS系統的快速建設與不斷完善，將形成全球分布的衛星導航系統，屆時BDS可見衛星數將增多，幾何分布結構改善，BDS自主定軌精度將大幅度提高；同時也將進一步體現BDS/GPS自主定軌的優勢與更廣泛的應用前景。

[1]YANG Yuanxi，LI Jinlong，XU Junyi.Contribution of the Compass satellite navigation system to global PNT users[J].Chinese Science Bulletin，2011，56(26): 2813-2819.doi:10.1007/s11434-011-4627-4.

[2]BERTIGER W，HAINES B，KUANG D，et al.Precise real-time low-Earth-orbiter navigation with the global positioning system(GPS)[EB/OL].(1999-05-26)[2015-08-26].http://ipnpr.jpl.nasa.gov/progress_report/42-137/137B.pdf.

[3]REICHERT A，MEEHAN T，MUNSON T.Toward decimeter-level real-time orbit determination: a demonstration using the SAC-C and CHAMP spacecraft[C]//The Institute of Navigation.Proceedings of the 15th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2002).Portland，Oregon:The Institute of Navigation，Inc.，2002:1996-2003.

[4]王甫紅.星載GPS自主定軌理論及其軟件實現[D].武漢：武漢大學，2006:27-32.

[5]ASHKENAZI V，CHEN W，HILL C J，et al.Real-time autonomous orbit determination of LEO satellites using GPS[C]//The Institute of Navigation.Proceedings of the 10th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1997).Kansas City，Missouri:The Institute of Navigation，Inc.，1997:755-761.

[6]MONTENBRUCK O，GILL E.Satellite orbits-models，methods，and applications[M].Springer:Verlag Berlin Heidelberg，2000:123-126.

[7]TAPLEY B D，RIES J C，DAVIS G W，et al.Precise orbit determination for Topex/Poseidon [J].Journal of Geophysical Research Oceans，1994，99 (12): 24383-24404.

[8]趙齊樂.GPS導航星座及低軌衛星的精密定軌理論和軟件研究[D].武漢：武漢大學，2004-11:36-42.

[9]楊元喜.自適應動態導航定位[M].北京：測繪出版社，2006:303-306.

[10]YANG Y，HE H，XU G.Adaptively robust filtering for kinematic geodetic positioning[J].Journal of Geodesy，2001，75(2/3):109-116.

Precision analysis on autonomous orbit determination with spaceborne BDS and GPS measurements for LEO satellite

XIONG Chao1，JIA Xiaolin2，3，ZHU Jun4，5，LU Chuanfang1

(1.Xi’an Aerospace Remote Sensing Data Technology Co.，Ltd.，Xi’an，Shanxi 710100，China；2.State Key Laboratory of Geo-information Engineering，Xi’an，Shanxi 710054，China；3.Xi’an Research Institute of Surveying and Mapping，Xi’an，Shanxi 710054，China；4.State Key Laboratory of Astronautic Dynamics，Xi’an，Shanxi 710043，China；5.Xi’an Satellite Control Center，Xi’an，Shanxi 710043，China)

In order to further study on the autonomous orbit determination of LEO satellite with BDS and GPS receiver，the paper discussed the mathematical models of autonomous orbit determination with spaceborne BDS and GPS measurements，presented a method of Helmert variance component estimation considering dynamical model，and then put forward the principle and the process of autonomous orbit determination in details.Based on the self-developed program，the feasibility and precision of autonomous orbit determination were analyzed using the stimulated BDS and GPS measurements generated by high dynamic signal simulator.Result showed that Helmert variance component estimation considering dynamical model could not only resolve the optimal weight of BDS and GPS measurements successfully，but also weaken the impact of gross errors effectively，thus to improve the precision of orbit determination.

autonomous orbit determination；extended Kalman filter；variance component estimation

2015-10-22

國家自然科學基金項目(11503096)；中國博士后科學基金項目(2015M572691)；地理信息工程國家重點實驗室基金項目(SKLGIE2014-M-2-3)。

熊超(1986—)，男，湖北麻城人，工程師，研究方向為衛星精密定軌和精密定位。

10.16547/j.cnki.10-1096.20160315.

P228

A

2095-4999(2016)03-0069-08

引文格式：熊超，賈小林，朱俊，等.星載BDS/GPS低軌衛星自主定軌精度分析[J].導航定位學報，2016，4(3):69-76.(XIONG Chao，JIA XiaoLin，ZHU Jun，et al.Precision analysis on autonomous orbit determination with spaceborne BDS and GPS measurements for LEO satellite[J].Journal of Navigation and Positioning，2016，4(3):69-76.)