Hadoop下基于貝葉斯網絡的氣象數據挖掘研究

王　昊，師　衛，李　歡（太原理工大學信息工程學院，太原030024）

Hadoop下基于貝葉斯網絡的氣象數據挖掘研究

王昊，師衛*，李歡
（太原理工大學信息工程學院，太原030024）

為了提高傳統樸素貝葉斯分類器對氣象數據挖掘的精度，擁有更高的處理海量數據的效率，提出了一種Hadoop平臺下基于離散貝葉斯網絡的數據挖掘改進算法。算法不要求屬性之間相互獨立，且充分結合Hadoop平臺適應處理大數據的優點，利用海量數據選取預測因子來訓練貝葉斯網絡分類器模型，以達到預測溫度的目的。實驗結果表明，算法不但預測精度明顯高于目前短期氣候預測中采用的樸素貝葉斯算法，而且極大地提高了運算效率。

數據挖掘；貝葉斯網絡；Hadoop；MapReduce；氣象預測

自古以來氣象預報在防災減災和國民經濟建設中都發揮著巨大作用，隨著社會經濟的發展和人民生活水平的提高，如何更加準確高效的進行天氣預測也越來越重要［1］。

傳統基于樸素貝葉斯分類器［2］的氣象預測算法在處理大規模數據時缺點越來越突出，主要表現為：一是沒有充分考慮到氣象屬性的特點，仍以屬性之間互不相關為基本出發點；二是隨著氣象預報要求的不斷提高，氣象數據計算規模急劇膨脹，其處理數據的效率已不能適應現代天氣預測的要求。

針對上述不足，本文提出Hadoop［3］下基于貝葉斯網絡的氣象預測算法。該算法以貝葉斯網絡［4］為理論依據，在Hadoop平臺下，利用MapReduce［5］對貝葉斯網絡結構學習中的預處理、模型訓練和精度評估3個過程進行分布式并行處理，充分利用了海量的氣象數據中蘊藏的大量有價值的信息。

1　貝葉斯網絡

1.1樸素貝葉斯分類器和貝葉斯網絡分類器

樸素貝葉斯分類器（Native Bayes）［6］是基于貝葉斯公式的一類簡單概率分類器，它以各個屬性間的條件獨立性假設為前提，假定特征向量的各分量間相對于決策變量是相對獨立的，也就是說各分量獨立地作用于決策變量，因此構造過程簡單，具有錯誤率小、穩定、健壯性強等特點。在氣象數據量小的時代，這種條件獨立假設還能保持比較高的準確性，但是在海量氣象數據面前，這種假設的缺點變得越來越明顯。

與樸素貝葉斯所不同，貝葉斯網絡是一種概率網絡，是基于概率推理的圖形化網絡，貝葉斯公式是這個概率網絡的基礎。它采用圖形化的網路結構直觀地表達變量的聯合概率分布及其條件獨立性，一個貝葉斯網絡是一個有向無環圖，由代表變量結點及連接這些結點的有向邊組成。

一個完整的貝葉斯網絡是由一個二元組B=（BS，BP），BS是貝葉斯網絡結構，包括網絡結構中的節點集合A，每一節點表示特定域中一個特征屬性，還包括有直接關系的節點之間的有向邊E，BP是每一節點都附有與該變量相聯系的條件概率分布函數（CPT），如果變量是離散的，則它表現為給定其父節點狀態時該節點取不同值的條件概率表（CPT），表示它們之間的概率依賴關系，當節點X沒有父節點時，節點X的CPT中只有X的先驗概率P（X），當節點X有k個父節點｛Y1，…，Yk｝時，節點X的CPT中是條件概率P（X|Y1，…，Yk）。可見，貝葉斯網是一種表示數據變量之間潛在關系的定性定量的方法，它使用這種圖形結構制定了一組條件獨立的聲明和用于刻畫概率依賴強度的條件概率的數字值。

1.2貝葉斯網絡學習

貝葉斯網絡具有牢固的數學基礎，Pearl在其［1988］的專著［7］中奠定了貝葉斯網絡的了基礎理論。其中給出并證明了如下定理：

對給定的概率分布P（x1，…，xn），存在P的貝葉斯網絡G，使，其中πxi是Xi的父結點集∏xi的配置。

貝葉斯網絡學習一般包含兩個內容，貝葉斯參數學習和貝葉斯結構學習，而貝葉斯網絡學習的核心是對貝葉斯網絡結構的學習。現在最流行的貝葉斯網絡結構學習方法可分為兩類，一類是基于搜索評分的學習方法，此方法過程簡單規范，易于操作，但由于搜索空間大，一般只適用于變量少或在一定范圍內的結構學習；還有一類是基于約束測試的學習方法，此方法過程比較復雜，但在一些假設下學習效率較高，而且在耗時方面，它往往要更快一些。現有的約束測試方法中，冗余邊檢測是在確定邊的方向之前進行，這樣無法準確地確定切割集，這就導致大量的高維條件概率計算，這樣經常不能定向所有的邊，這些都降低了學習效率和準確性［8］。

本文在此基礎上提出了基于預測能力的貝葉斯網絡學習方法。

1.3基于預測能力的貝葉斯網絡學習

因為預測能力就是預測正確率，預測能力相同是條件獨立性的充分必要條件［9］，這樣預測能力便把變量之間弧的存在性與方向有機的結合在一起。此結構學習算法首先依次計算兩個變量之間的預測能力，再根據條件預測能力確定弧的存在性及方向。

設有離散隨機變量X1，X2，…，Xn，x1，x2，…，xn為變量的值；D是變量X1，X2，…，Xn產生的大小為N的隨機數據集。

將F（Xi→Xi）定義為變量Xi的自預測能力，F^（Xi→Xi）記作F（Xi→Xi）的估計值；

將F（Xm1，…，Xmt→Xi）定義為變量 Xm1，…，Xmt對變量 Xi的預測能力，F^（Xm1，…，Xmt→Xi）記作F（Xm1，…，Xmt→Xi）的估計值。

第1步確定貝葉斯網絡的初始結構

Xj→Xi；

Xi→Xj

第2步對初始結構進行調整

如果P（X|Y1，…，Yk）＞ρz，則添加弧Xj→Xi；

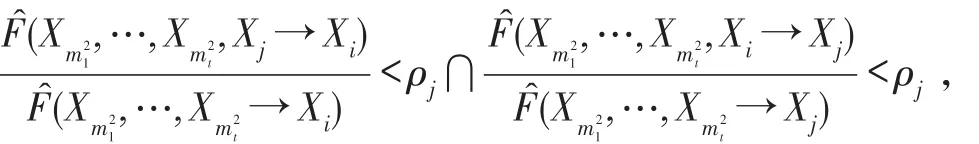
則刪除Xi→Xj之間的弧；

定向為Xj→Xi；

第3步進行環路檢驗［11］

在經過第二步調整過的結構圖中，我們要把沒有父結點或沒有子結點的結點和與他們相連的弧刪除，在剩下的子圖中依照剛剛的做法把這些結點和弧都刪除，這樣一直做下去，若始終沒有出現一個每個結點都既有父結點又有子結點的子圖，則說明結構圖不存在環路。否則，存在環路。

2　本文算法實現

針對溫度氣象數據集特征，基于MapReduce改進貝葉斯網絡算法的過程包括：數據預處理、模型訓練和精度評估三大過程。其流程圖如圖1所示。

圖1　算法流程圖

2.1數據預處理

（1）數據清洗

氣象數據質量的好壞直接影響著氣象領域中數據挖掘的準確度。實驗中采集到中國地面氣候資料日值數據集中，存在缺省漏測和格式不一致的數據值，這嚴重影響到數據挖掘算法的執行效率，甚至有可能導致挖掘結果的偏差，故需要對數據集進行清洗。首先，基于MapReduce編程模型，統計含有缺失值的數據條數，結果顯示日值數據集中含有缺失值的數據條數占總條數不到1%，因而直接采用把不完整的數據全部剔除出數據集；其次，基于MapReduce編程模型，對數據格式不一致的數據進行格式轉換。最終使得數據集中的每一條數據都是格式一致的和完整可靠的。

（2）預測因子選擇

基于MapReduce編程模型完成對溫度和其他氣象要素之間的相關性分析，選取合適的預測因子。對于任意兩個氣象要素X和Y，其相關系數的計算公式為：

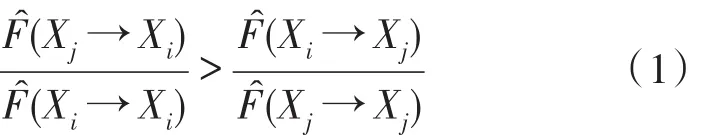
γXY取值在-1到1之間。當γXY=0時，稱X與Y不相關；當|γXY|=1時，稱X與Y完全相關，此時，X與Y之間具有線性函數關系；當|γXY|＜1時，X的變動引起Y的部分變動，γXY的絕對值越大，X的變動引起Y的變動就越大，一般情況下當|γXY|＞0.8時為高度相關，當0.5＜|γXY|＜0.8時為顯著相關，當0.3＜|γXY|＜0.5時為低度相關，當|γXY|＜0.3時為不相關。

（3）數據離散化和整理

根據氣溫在一年中的分布情況，把氣溫按照溫度的高低分為寒冷（-15℃以下），涼爽（-15℃～0℃），溫和（0℃～15.9℃），暖和（15.9℃～25℃），炎熱（25℃以上）5個級別。

數據預處理分為兩個任務，一個是離散化預測因子，另一個是輸出整理數據與溫度分級標識。這兩個任務是獨立的，因此將這兩個過程作為并行的MapReduce任務完成，定義Step1負責預測因子的區間離散化，定義Step2負責輸出數據整理與溫度分級標識。

①Step 1預測因子在數據集中以數字值的形式描述，因此需要對預測因子進行離散化操作。首先對預測因子和預測目標做標識，如下表所示：

離散過程中，我們采用PKI算法［12］，其一般采取離散區間大小等于離散區間數量的方法，但是在數據量巨大且分布不均勻的情況下，離散區間大小過大，會使得有些區間內沒有值。針對氣象數據大而不均的特點，我們令k=，以達到擴大區間的目的。

基于MapReduce編程模型完成統計預測因子的最大值和最小值，因此各個預測因子的離散化區間寬度w表達式如下：

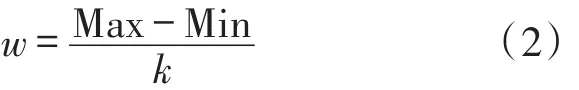
②Step 2輸出數據需要進行整理，定義當前日期為t，則前一日為t-1，整理后每一行數據為（t-2，t-1，t）的各個預測因子和明日的氣溫等級。Hadoop框架中的MapReduce的shuffle過程會將相同的key值放在一起，可以將t-2，t-1，t的各個預測因子所生成的key值設置為待連接的每一行，然后MapReduce框架會自行將其連接起來。

2.2模型訓練

一般情況下，為了提高數據挖掘的準確度，將數據預處理中的J2整理的數據集分為兩部分：80%訓練集和20%測試集，訓練集用于訓練貝葉斯網絡模型，測試集用于測試貝葉斯網絡分類模型的精度。模型訓練過程中，分為兩大任務，一是統計各個溫度級別頻率和各個預測因子頻率，另一是根據統計的頻率計算各個預測因子之間以及預測因子與預測目標之間的預測能力，后一次的過程依賴于前一次的頻率統計結果。

根據計算出的預測能力，運用第1節提出的算法，經過確定初始貝葉斯結構、調整初始貝葉斯結構和環路檢驗3個步驟，最終確定出貝葉斯網絡的結構。

2.3精度評估

精度評估MapReduce過程中，將測試集分割成多個小塊，對每一小塊中各行數據通過分類模型進行預測，將預測結果與測試集中的溫度真實數據進行比較，記錄其正確與否的情況。最后用MapReduce統計預測情況，計算出正確率和預測率，公式如下：

正確率=正確分類數/實際分類數預測率=正確分類數/真實分類數在精度評估過程中，通過式（3）

預測分類時，由于數據量大且分布不均，導致大量的條件概率相乘后，引起浮點數結果下溢的情況，因此對上式兩邊用求對數做處理，則c可表示為式（4）

精度評估結果不理想時，需對模型重新訓練，直到結果可以接受為止。

3　實驗分析

3.1實驗環境和數據

本文實驗環境基于Hadoop云平臺，采用完全分布式模式搭建于9臺普通PC機上，其中一臺為NameNode，其余八臺作為DataNode。電腦的配置如下：3.4 GHz雙核CPU、4 G內存、150 G磁盤、Linux CentOS 6.0操作系統、Hadoop 1.0.2版本。

研究數據來自中國的氣象數據共享服務體系從1951年到2014年的環境數據，包括降水量、平均氣溫、平均氣壓、平均風速、平均相對濕度、日照時數、最大風速、最大風速的方向等其他因素。我們試驗采取的數據是太原市從1951年到2014年底的全部數據。

3.2實驗結果與分析

（1）相關性分析

首先通過對數據的清洗，把原來不完整、格式不正確的數據全部剔除出我們的數據庫。然后對各類各類預測因子進行標識，并計算它們與氣溫之間的相關系數。計算結果如表1所示。

表1　各個氣象要素與平均氣溫之間的相關系數

我們在試驗中選取|γXY|＞0.3的氣象要素作為預測因子，他們分別是平均氣壓B、平均水汽壓D、日最低氣溫G、日最高氣溫H和小型蒸發量I，平均氣溫是我們的目標因子，我們用字母R作為它的標識。

（2）模型訓練

取 ρc=ρz=ρj=1.1，根據計算出的變量之間的預測能力，得到初始的貝葉斯網絡結構圖，如圖2所示。

調整貝葉斯網絡結構，經過調整后的貝葉斯網絡結構如圖3所示。

圖3　調整后的貝葉斯網絡結構圖

（3）精度評估

本實驗的正確率和預測率如表2所示，其中R0代表寒冷，R1代表涼爽，R2代表溫和，R3代表暖和，R4代表炎熱。

表2　正確率和預測率

圖4和圖5分別展示了本算法和短期預測的樸素貝葉斯分類方法在正確率和預測率方面的對比，通過圖形可以看出，不管是在正確率方面還是在預測率方面，本文算法都有較大的優勢。

圖4　正確率對比圖

圖5　預測率對比圖

（4）效率評估

為了驗證本文方案在海量氣象數據情況下的運行效率，如圖5，我們采用加速比對集群執行時間與單機時間進行對比。加速比公式定義為：

加速比=單機執行時間/集群執行時間

如圖6所示，在數據量較大的情況下，本文方案的加速比接近于線性加速比。隨著節點數的增多，對海量數據訓練的加速優勢也就越明顯。

圖6　加速比曲線

4　結語

本文對Hadoop下基于貝葉斯網絡的氣象數據挖掘進行了研究，給出了一種基于預測能力的離散貝葉斯網絡結構學習和Hadoop相結合處理數據的新方法，該方法具有以下特點：（1）可以充分利用大數據時代下的海量數據，有效避免信息丟失及假依賴的出現（2）運算效率及準確率高于常規預測方法（3）不要求預測因子相互獨立等，對預測因子要求不高（4）能夠處理不完全、不精確或不確定訓練數據集。在數據量不斷飛漲的今天，此算法提供了在海量數據中挖掘有用的信息的新思路，其在電子商務、移動互聯網、反恐等諸多領域的應用值得進一步研究。

［1］ 樊改娥，張順利.淺談氣象預報的作用［J］.科技情報開發與經濟，2008，18（16）：217-218.

［2］ 張晨陽，劉利民，馬志強.云計算下基于貝葉斯分類的氣象數據挖掘研究［D］.內蒙古：內蒙古工業大學，2014.

［3］ 李斌，張建平，劉學軍.基于Hadoop的不確定異常時間序列檢測［J］.傳感技術學報，2015，28（7）：1066-1072.

［4］ 史志富，郭曜華.機載光電系統目標威脅估計的模糊貝葉斯網絡方法［J］.傳感技術學報，2011，24（11）：1584-1589.

［5］ Kadirvel SELVI，Fortes JAB.Towards Self-Caring MapReduce：A Study of Performance Penalties Under Faults［J］.Concurrency and Computation-Practice&Experience，2015，27（9）：2310-2328.

［6］ 趙力.基于貝葉斯壓縮感知的說話人識別方法［J］.電子器件，2015，38（5）：1135-1137.

［7］ Peal J.Fusion ProPagation and Structuring in Belief Network［J］. Artificial Intelligence，1986，29：241-288

［8］ 馬明，劉浩然.貝葉斯網絡算法研究及應用［D］.秦皇島：燕山大學，2014.

［9］ 張劍飛，王輝，王雙成.基于預測能力的貝葉斯網絡分類器學習［J］.計算機應用研究，2007，24（8）：50-52.

［10］Lam W，Bacchus F.Learning Bayesian Belief Network：An Approach Based on the MDL Principle［J］.Computational Intelligence，1994，10：269-293.

［11］李碩豪，張軍.貝葉斯網絡結構學習綜述［J］.計算機應用研究，2015（3）：641-646.

［12］Yang Y，Webb G I.Weighted Proportional k-Interval Discretization for Naive Bayes Classifiers［C］//The 7th Pacific-Asia Conference on Knowledge Discovery and Data Mining（PAKDD），2009：501-512.

王昊（1989-），男，漢族，河北省保定人，太原理工大學信息工程學院，碩士研究生在讀，主要研究方向為大數據挖掘，wanghao_tyut@163.com；

師衛（1956-），男，漢族，山西省朔州人，太原理工大學信息工程學院，副教授，主要研究方向為嵌入式系統研究、大數據挖掘，shi_w@163.com。

The Research of MeteorologicalData Mining Using Bayesian Network Based on Hadoop

WANG Hao，SHI Wei*，LI Huan
（Taiyuan Uniυersity of Technology Institute of Information Engineering，Taiyuan 030024，China）

In order to improve the precision of themeteorological datamining using raditionalnaive bayesian classifier，and own a higher efficiency ofhandling the huge amountsof data，this paper proposes an improved algorithm of discrete Bayesian network to predict the temperature.This algorithm can eliminate theweakness of naive bayesian method on the premise thatattributes are independentof each other，and combine the characteristics of the Hadoop platform processing large data.Usingmassivemeteorological data，it selects predictors and trains the Bayesian network classificationmodelon Hadoop platform.The experiments show that the improved algorithm isnotonly the accuracy is significantly higher than the short-term climate prediction using Naive Bayesian analysis，regression analysisand clusteranalysismethod，butalso improves the efficiency of the algorithm greatly.

datamining；bayesian network；hadoop；mapreduce；weather prognosis

TP301.6

A

1005-9490（2016）04-0841-06

2015-09-13修改日期：2015-11-19

EEACC:614010.3969/j.issn.1005-9490.2016.04.018