三角恒等變換和解三角形，想說愛你不容易
——有感于高一習題課中一個習題的數學

李雪嬌（浙江省臨海市杜橋中學）

三角恒等變換和解三角形，想說愛你不容易
——有感于高一習題課中一個習題的數學

李雪嬌
（浙江省臨海市杜橋中學）

三角恒等變換和解三角形是高中數學的重要內容之一，因此三角恒等變換與解三角形是三角函數部分的重要內容，也是這幾年浙江省數學高考必考的一個重要知識點。

三角恒等變換；解三角形；正弦定理；余弦定理；數學思想

在高考的大背景下，三角恒等變換及解三角形的教學是個重要內容。考查時以中、低檔題為主，是高考得分的關鍵點，筆者對所在的學校高三學生解答三角題目的得分做了長期的統計，發現得分率并不高，容易出現這樣那樣的錯誤，解答題得滿分的學生較少，我常把這種現象叫做“三角，想說愛你不容易！”針對高三出現的這種現象，筆者分析高一的學習是關鍵，要從高一開始做起，打好基礎。下面是筆者在高一必修5一節復習課時對例題的設計和講解，以此來復習和強化三角恒等變換及解三角形的知識。

例題：在△ABC中，角A，B，C的對應邊為a，b，c且c cos B+ b cos C=2a cos B

分析：將已知條件進行轉化，找到比較明顯的邊的關系或角的關系.這類問題通常需要運用正弦定理或余弦定理，并結合三角恒等變換公式將條件中的邊角關系統一到邊的關系或角的關系，即“角化邊”或“邊化角”.“角化邊”或“邊化角”是解決這類問題常見的思維出發點.

（1）對于式子c cos B+b cos C=2a cos B，可以有以下幾種解法，

可對其利用正弦定理得到sin C cos B+sin B cos C=2sin A cos B即

或者也可利用余弦定理得到

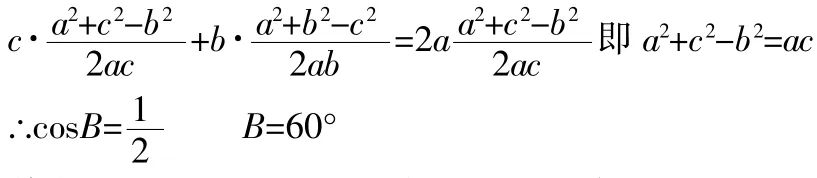
其實c cos B+bcos C是向量投影概念的應用，即c cos B+bcos C=a，

所以由c cos B+bcos C=2a cos B馬上得到所以B=60°

（2）由（1）知B=60°，先用余弦定理b2=a2+c2-2a cos B求得ac，再可以用面積公式計算出結果。

我們的學生在（2）小題中存在的困惑是選擇公式時不夠準確，糾結在余弦定理和面積公式三個式子里選擇哪個，筆者在教學中教給他們一個不是規定的約定，就是已知哪個角就用含有這個角正弦值的面積公式，用含有這個角余弦值的余弦公式。學生掌握得也較快。下面是對（2）小題進行變式：

變6：若在開始的條件中，改變成在銳角△ABC中，那么從“變1～變5”中哪些結果會變。

分析：來看變2和變3，此題可以先寫出余弦定理b2=a2+c2-2ac cos B，再用基本不等式可得，又因為三角形兩邊之和大于第三邊得到

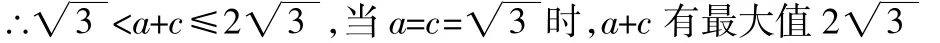
來看變4，此題可以先寫出余弦定理b2=a2+c2-2a cos B，再用基本不等式得到3=a2+c2-ac≥ac當a=c時（ac）max=3，進而能求出面積的最大值。

但是當有了“銳角三角形”這個條件的限制時，用基本不等式還要會再加其他的條件來進行求范圍，顯得有點麻煩，對于高一的學生有些難以接受。所以筆者就針對高一學生的知識儲備和知識結構，對上述的幾個變式采用了邊到角的轉化，實現了兩條邊（即兩個未知量）到一個角（即一個未知量）的轉化。

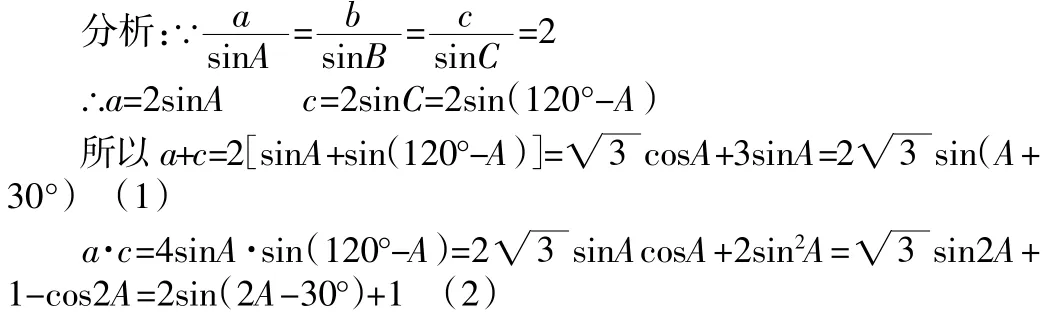
若是任意三角形，則A的范圍容易確定0°＜A＜120°，則利用三角函數知識能求得（1）式和（2）式的范圍。

若三角形是銳角三角形，則確定A的范圍是關鍵，也是一個難點。因為是銳角三角形，所以三角形的三個內角都必須是銳角，可做這樣的限制。

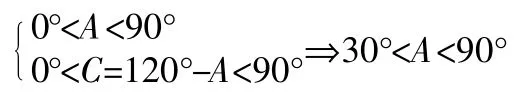
再利用三角函數知識能求得（1）式和（2）式的范圍。

評注：

1.易錯點撥。在解題過程中，由于三角恒等變換和解三角形中公式眾多需靈活運用，且常需要對角的范圍及三角函數值的符號等進行討論，甚至需要對題設中的隱含條件進行挖掘，故解題時稍有不慎，就會出現漏解、增解等現象。合理運用三角公式是解決三角函數的圖象與性質、三角求值及解三角形這幾類問題的關鍵。高一的學生還要不斷地進行訓練。

2.利用數學思想方法進行變換。數學思想與方法是數學知識在更高層次上的概括，利用它來指導我們解題，會讓我們思維頓開。它蘊涵在數學知識發生、發展和應用的過程中，本題用到的思想方法主要有轉化與化歸思想、整體化思想、特殊與一般化思想。

下面是我為上述這個例題準備的反饋練習：

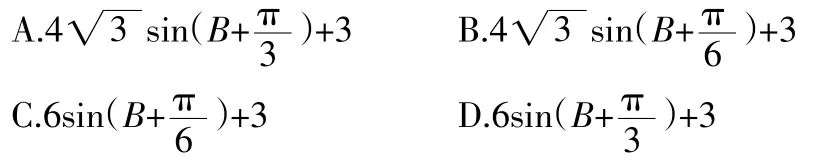
在選出的選項中求周長的最大值________；

……

通過本題的教學，學生收獲比較大，本題目比較綜合，將三角恒等變換和解三角形綜合在一起，題中用到了恒等變換中的變角、降冪、輔助角公式、正弦定理、余弦定理，并能運用正、余弦這兩個定理解決周長和面積問題。通過變式講解，反饋題目做得較好，效果不錯。

在高中數學解題中，變換是其主要工具之一，通過變換能夠將復雜公式簡單化，簡單明了，通過變換能將復雜問題簡單化，利于學生理解。總之，解答三角恒等變換的題目的方法多樣，萬變不離其宗，要注意靈活運用，最后借用名師教給我們的口訣，要努力做到“三看”，即

（1）看角，把角盡量向特殊角或可計算角轉化；

（2）看名，把一道等式盡量化成同一名稱或相近的名稱，例如把所有的切都轉化為相應的弦，或把所有的弦轉化為相應的切；

（3）看式，看式子是否滿足三角函數的公式。如果滿足直接使用，如果不滿足轉化一下角或轉換一下名稱，就可以使用。

·編輯謝尾合