基于磁梯度張量的共軛梯度3D約束反演

李金朋，張英堂，范紅波，李志寧，尹　剛

(解放軍軍械工程學院，河北 石家莊　050003)

?

基于磁梯度張量的共軛梯度3D約束反演

李金朋，張英堂，范紅波，李志寧，尹剛

(解放軍軍械工程學院，河北 石家莊050003)

針對傳統鐵磁物質反演方法存在反演結果多解性的問題，提出了基于磁梯度張量的共軛梯度3D約束反演方法。該方法在經典Tikhonov正則化理論框架下，引入粗糙度矩陣對反演模型進行約束以避免反演過程中的多解性問題；針對磁梯度張量數據深度分辨率差、容易出現“趨膚效應”的問題，在模型目標函數中引入深度加權矩陣提高縱向分辨率；通過引入懲罰泛函，在反演迭代過程中去除方程的病態解，使反演結果更好地與原始模型相吻合。仿真驗證表明：該反演方法能夠反映磁性異常體的輪廓形態，具有較好的橫向和縱向分辨率。

磁梯度張量；共軛梯度；粗糙度矩陣;深度加權矩陣

0　引言

磁性目標反演技術是通過地面或航空等實測數據，利用某種手段推算出磁性體(未爆彈、水雷、潛艇等)在地下的分布信息。磁法勘探具有探測精度高、虛警率低、定位能力強等優點。運用磁探測技術可以對地下或者水下小尺度磁性目標進行定位與識別[1]，為下一步的工作提供數據支持。磁梯度張量場是指磁場三分量在三個坐標方向上的變化率，共有9個分量。相比磁總場、磁總場梯度和磁場三分量數據，磁梯度張量場不但具有更高的分辨率，而且包含可以聯合解釋的多個分量，能更好地描繪場源的空間形態及位置[2]。

國內外眾多研究學者針對三維反演成像展開了大量的工作。1972年,Nabighian將解析信號運用到二維剖面磁場數據解釋中，隨后又應用于三維網格情況[3-4]。2013年，吉林大學孟慧在磁梯度張量數據解釋方面研究了解析信號法，通過仿真實驗表明解析信號法能突出淺部磁場特性[5]。1982年，Thompson利用二維歐拉反褶積識別法對二維剖面數據進行解釋。1990年，Reid等人將二維反演方法推廣到三維磁場數據解釋中，能夠對大范圍的平面網格數據進行反演[6-7]。2008年，吳招才將該方法應用到多目標識別，仿真表明識別效果較好[8]。1997年由Patella[9]首次提出概率成像法。郭良輝根據概率成像概念提出了重力數據三維相關成像法并將其推廣到磁法數據的相關成像，提出了磁總場異常相關成像法，并通過建模仿真驗證了該方法的有效性[10-11]。2002年，Portniaguine和Zhdanov提出了聚焦反演法，并將其應用于磁化率成像和重力梯度反演[12-13]。

但是，以上反演方法研究存在方程解的不唯一性及成像結果的“上漂”現象等問題，使得傳統反演方法在實際應用中受到限制。針對此問題，本文提出基于磁梯度張量的共軛梯度3D約束反演。

1　磁梯度張量正演理論

1.1磁梯度張量要素

與傳統的磁總場異常相比，磁梯度張量能提供更加豐富的異常信息，能更好的反映地下磁性體的細節特征。磁梯度張量可以由一個二階矩陣表示為：

(1)

式(4)中：G為磁梯度張量；Bαβ(α,β=x,y,z)為磁梯度張量的分量，共有9個；根據場論可知:Bxy=Byx,Bxz=Bzx,Byz=Bzy,Bxx+Byy+Bzz=0。因此，磁梯度張量的9個分量只有5個是獨立的。

1.2長方體正演公式

建立笛卡爾坐標系。x,y軸為水平軸，z軸為垂直向上軸。設x方向為a，y方向為b，z方向為c的直立長方體，長方體中心坐標為(x0,y0,z0)。M為長方體磁化強度，點(x,y,z)為觀測點。則長方體磁異常及梯度正演公式如下：

(2)

(3)

(4)

(5)

(6)

(7)

式中，cosαs，cosβs，cosγs為磁化強度M的方向余弦，u0為真空磁導率，(ξ,u,ζ)為長方體單元角點坐標。

2　基于磁梯度張量的共軛梯度3D約束反演

將地下待測空間劃分成大小相等、緊密排列、物性參數為常數且相等的長方體，觀測點與單元體中心到地面的投影一一對應，各觀測點實際測量所得磁梯度張量分量數據為所有長方體相應分量的和，用線性公式表示為：

d=A×m

(8)

式(8)中，矩陣A的元素Aij為第i(i=1,2,3,…,p)個觀測點觀測的第j(1,2,3,…,n)個單元的響應；p×1維的行向量d為任意張量分量數據，m為待反演參數。

傳統的磁梯度張量場反演等價于求解線性方程(8)的反問題，由于采集數據d遠小于待反演參數m，因此該方程是欠定的，方程組的解不唯一且不穩定。根據Tikhonov正則化理論，構建三維目標函數:

(9)

2.1粗糙度矩陣

針對病態方程的多解性問題，本文將模型粗糙度矩陣引入磁梯度張量的三維反演中，通過補充先驗數據信息，將目標函數轉化為非病態問題，使得反演模型能夠在三個方向上光滑過渡。定義粗糙度矩陣R為m(r)在x,y和z方向的一階偏微分的平方和，即：

(10)

2.2深度加權矩陣

根據磁梯度張量正演公式(2)—式(7)可知，反演方程的核函數隨著距離的增大而快速衰減，而在構造極小化模型目標函數‖m‖2=∫m2dV時，重構模型的核函數是線性的。因此如果不對模型進行約束就會使反演結果出現“趨膚效應”，在進行模型重構時使模型多集中于地表很難反演出真實構造。因此，本文通過引入深度加權因子來抵消核函數隨深度增大的衰減量，即：

(11)

式(11)中，z為地下網格單元體中心坐標；z0和β為常數。β為經驗值一般取2～4;z0取決于塊體單元的尺寸以及觀測面的高度。

將公式(11)及目標函數最小化模型構造帶入公式(10):

(12)

式(12)中，αs,αx,αy和αz為模型目標函數中的加權因子。將公式(12)按照模型區域網格剖分進行離散化得到：

(13)

式(13)中，Wi=αiRiZ(i=s,x,y,z)。Ri為有限元差分算子，Z為深度加權對角矩陣。將公式(13)代入式(9):

(14)

2.3懲罰泛函

在反演過程中，為了得到與實際情況更加吻合的物性參數分布，利用懲罰函數在反演迭代過程中去除病態解，對模型參數進行約束使反演結果控制在合理的范圍內：

(15)

2.4共軛梯度法

共軛梯度法是求解大型對稱正定線性方程最優化問題的高效解法。共軛梯度法最早是由計算數學家Hestenes和幾何學家Stiefel于1952年在解線性方程組時提出的。

其主要思想是，對稱正定線性方程組

Ax=b

(16)

的解與下述二次函數F(x)的極小值等價，

(17)

共軛梯度法就是基于這個二次函數推導得出的，過程從略，算法如下：

1)任意取初始向量x0，計算r0=b-Ax0，并取p0=r0。

2)對k=0,1,…,計算下列各項，

3)若‖rk+1‖≤ε，則停止計算，否則返回2)。

3　仿真分析

3.1單直立長方體模型

設地下模型空間尺寸xyz為21 m×21 m×10 m，將地下場源空間劃分為21×21×10=4 410個單元格，每個單元格均為邊長為1 m的正方體,地面觀測點為21×21=441個網格。地下空間存在1個異常體，長×寬×高為4 m×5 m×4 m，頂板埋深為3 m,底板埋深為7 m，磁化強度為40 A/m，模型與觀測點如圖1所示。假設模型體在垂直磁化條件下，觀測面位于地面0.1 m處，得到理論模型正演數據如圖2所示。利用所得正演數據，在僅考慮數據擬合泛函時，對理論模型進行反演。設置最高迭代次數為60次。對反演物性參數設置解區間[Mmax,Mmin]，在本例對磁梯度張量全張量反演獲得的磁化強度進行加權并設置統一的模型約束區間為[1,40]。從圖3可以看出，異常體反演的結果具有一定的橫向分辨率，但是對深度信息的反映較差，長方體反演模型多集中于地表，難以反映異常體的真實構造。

應用本文反演方法，在目標函數中加入深度加權函數及粗糙度矩陣。通過對比圖3和圖4結果可以看出：在加入深度加權函數和粗糙度矩陣后，能夠反映異常的深度信息，更好地反映了地下異常體的分布情況。

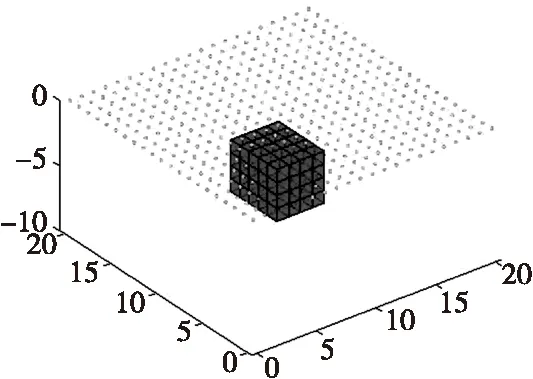
圖1　正演理論模型Fig.1　Forward theoretical model

圖2　單直立長方體磁梯度張量數據分布圖Fig.2　Single rectangular magnetic gradient tensor data map

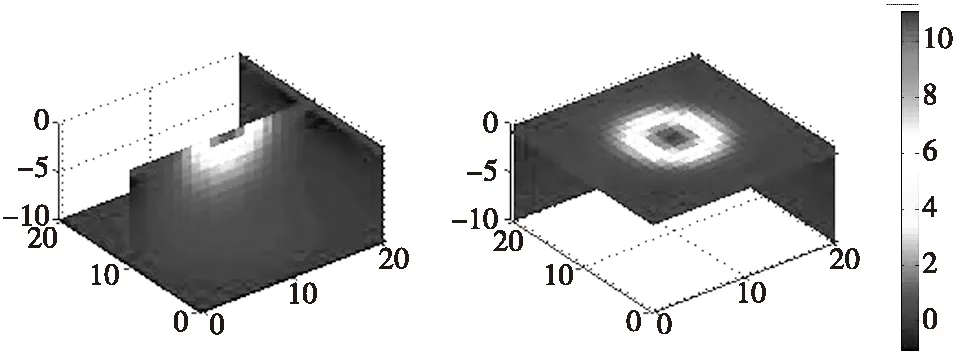
圖3　數據擬合泛函反演圖Fig.3　data fitting inversion map

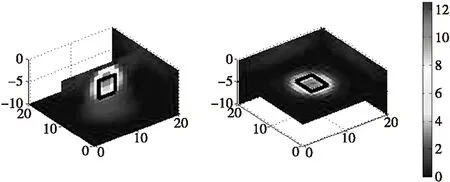
圖4　應用本文方法進行反演Fig.4　Inversion results by this method

3.2長方體組合模型

設地下模型空間尺寸xyz為21 m×21 m×10 m，將地下場源空間劃分為21×21×10=4 410個單元格，每個單元格均為邊長為1 m的正方體,地面觀測點為21×21=441個網格。地下空間存在2個長方體，分別由長×寬×高為7 m×7 m×7 m和8 m×9 m×9 m的長方體拼接而成，磁化強度為40 A/m，模型與觀測點如圖5所示。假設模型體在垂直磁化條件下，觀測面位于地面0.1 m處，得到理論模型正演數據如圖6所示。對反演物性參數設置解區間[Mmax,Mmin]，在本例對磁梯度張量全張量反演獲得的磁化強度進行加權并設置統一的模型約束區間為[1,40]。利用本文反演方法獲得的反演分布如圖7所示。從結果可以看出：該反演方法能夠反映長方體組合模型的輪廓形態，具有較好的橫向和縱向分辨率。

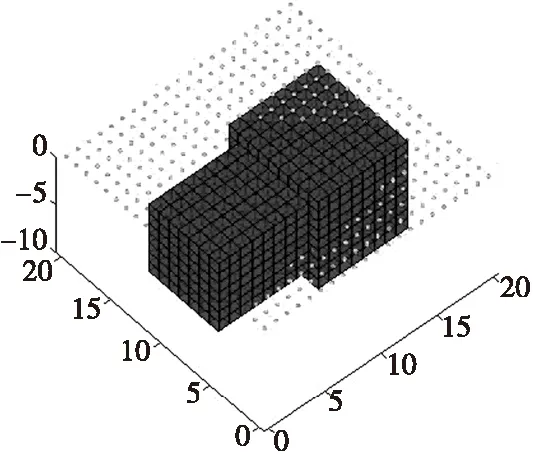
圖5　組合長方體模型Fig.5　Combination rectangular model

圖6　組合立長方體磁梯度張量數據分布圖Fig.6　Combination of rectangular magnetic gradient tensor data map

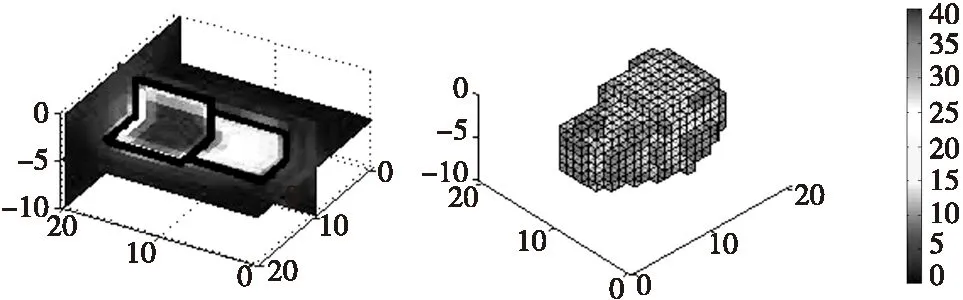
圖7　加約束后反演切片圖與空間立體結構圖Fig.7　Inversion slice and three-dimensional structure under constraint

4　結論

本文提出了基于磁梯度張量的共軛梯度3D約束反演方法。通過引入粗糙度矩陣有效地避免函數的多解性問題；利用深度加權矩陣約束函數，壓制了“趨膚效應”，提高了異常體的縱向分辨率；通過引入懲罰泛函，有效提高了解的有效性。仿真驗證表明：本文方法能夠較好地反映磁性異常體的輪廓形態，具有較好的橫向和縱向分辨率。不足之處在于只是通過仿真驗證了該方法的有效性，在工程實踐中的應用還有待進一步的補充和改進。

[1]卞光浪，翟國軍，黃謨濤，等.顧及地磁背景場的多目標磁異常分量換算方法[J].武漢大學學報，2011,36(8):914-918.

[2]張昌達.航空磁力梯度張量測量——航空磁測技術的最新進展[J].工程地球物理學報, 2007,3(5): 354-361.

[3]NabighianMN.Theanalyticsignaloftwo-dimensionalmagneticbodieswithpolygonalcross-section:itspropertiesanduseforautomatedanomalyinterp-retation[J].Geophysics, 1972,37(3):507-517.

[4]NabighianMN.Towardathree-dimen-sionalautomaticinterpretationofpotentialfielddataviageneralizedHilberttransfo-rms:Fundamentalrelations[J].Geophysics.,1984,49(6):780-786.

[5]孟慧.磁梯度張量正演、延拓、數據解釋方法研究[D]. 吉林：吉林大學儀器科學與電器工程學院，2012.

[6]ThompsonDT.EULDPH:Anewtechniqueformakingcomputer-assisteddepthestim-atesfrommagneticdata[J].Geophysics,1982,47(1):31-37.

[7]ReidAB,AllsopJM,GranserH,etal.Ma-gneticinterpretationinthreedimensionsusingEulerdeconvolution[J] .Geophysics,1990,55(1):80-91.

[8]吳招才.磁梯度張量技術及其應用研究[D].武漢：中國地質大學，2008.

[9]PatellaD.Introductiontogroundsurfaceself-potentialtomography[J].GeophysicalProspecting,1997,45:653-681.

[10]郭良輝，孟曉紅，石磊，等.重力和重力梯度數據三維相關成像[J].地球物理學報，2009,52(4):1098-1106.

[11]郭良輝，孟曉紅，石磊.磁異常ΔT三維相關成像[J].地球物理學報，2010,53(2):435-441.

[12]PortinaguineO,ZhdanovMS.Focusinggeophysicalinversionimage[J] .Geop-hysics,1997,64(3):874-887.

[13]PortinaguineO,ZhdanovMS.3-Dinv-ersionwithdatacompressionandimagemagneticfocusing[J].Geophysics, 2002,67,(5):1532-1541.

3D Constrained Inversion of Conjugate Gradient Based on Magnetic Gradient Tensor

LI Jinpeng, ZHANG Yingtang, FAN Hongbo, LI Zhining, YIN Gang

(Ordnance Engineering College, Shijiazhuang 050001, China)

For the problem that the inversion results of conventional inversion methods of ferromagnetic material have multiple solutions due to qualitative equations, we proposed a method of 3D constrained inversion of conjugate gradient based on magnetic gradient tensor. Firstly, in order to avoid the problem of multiple solutions, we used the roughness matrix in the classical Tikhonov regularization under the framework of the theory. Then, for the magnetic gradient tensor data had poor depth resolution and problem of “skin effect”, we used depth weighting matrix introduced in the objective function to improve the vertical resolution. Finally, we removed solution of the equation in the inversion iterative process, so that the inversion results coincided with the original model better, by introducing the penalty functional. Simulation result showed that this inversion method could reflect the outline shade of the magnetic anomaly and has good lateral and vertical resolution.

magnetic gradient tensor; conjugate gradient; roughness matrix; depth weighting matrix

2016-01-13

李金朋(1991—)，男，吉林長春人，碩士研究生，研究方向：測試技術與信號處理。E-mail:18626648671@163.com。

P631

A

1008-1194(2016)04-0088-05