三維重力異常的正則化反演

劉　堯，李延清，陶鵬飛，胡尊平

（新疆維吾爾自治區地質調查院，新疆烏魯木齊830000）

三維重力異常的正則化反演

劉堯*，李延清，陶鵬飛，胡尊平

（新疆維吾爾自治區地質調查院，新疆烏魯木齊830000）

以BG理論為基礎，將該理論與吉洪諾夫正則化方法相結合，應用于重力異常三維反演中，用來確定地下場源的密度分布和質心坐標。針對位場缺少深度上的分辨能力、垂向分辨率低這一問題，聯合地面和航空測量的數據組成三維重力異常數據，對地下地質模型參數進行等維反演，即用三維重力異常數據反演地下三維的地質模型參數。用于反演的異常數據包含了不同高度上的重力觀測數據，與傳統的反演方法相比，相當于增加了數據維數，在一定程度上有效改善了垂向分辨率低這一問題。

重力異常；正則化；三維反演；線性反演

1　概述

地球物理場是由地下地質體引起，因此場的分布也就反映了地下地質體的分布特征。地球物理反演就是利用地面觀測到的地球物理場的異常數據來推測地下地質體的分布，即根據觀測數據求取相應的地球物理模型［1-2］。眾所周知，位場數據不能很好反映地質體的垂向分布信息，反演結果深度分辨率低，這是因為實際觀測數據總是有限個數據體，而地球物理模型是連續的介質模型。地球物理反演時，需要將連續的地球物理模型進行離散化，根據離散數據來求取離散模型。觀測數據一般是一條剖面或一個平面上的離散數據，而相應的模型是二維或三維的連續介質模型，這樣就導致我們經常采用一維的觀測數據反演二維的地球物理模型，或者采用二維的觀測數據反演三維的地球物理模型，最終使得反演結果的垂向分辨率低［3-5］。

針對重磁位場反演結果垂向分辨率低這一問題，介紹了一種新的位場反演方法，即“等維反演”。“等維反演”所采用的異常數據體包含了不同高度上的位場觀測數據，這相當于增加了“數據維”，實現了用三維數據反演三維模型，必然能夠提高反演結果垂向分辨率低的問題［4-5］。不同飛行高度上的航空重磁測量數據，聯合地面觀測數據即可構成等維反演的三維的異常觀測數據［6-7］。

2　位場正則化線性反演理論

在許多地球物理學問題中，觀察數據和模型之間存在線性泛函關系，并可以通過第一類弗雷德霍姆方程表示。根據觀察數據和模型參數的個數不同，方程可能為不同的類型。當方程為欠定時，解不唯一，可以通過多種方法構制不同的模型［8-9］。根據BG理論，引入加權函數和拉格朗日乘數，構制最小長度解模型：

通過變分原理，可得該無條件極值問題的解模型。進一步分析該泛函模型，可知方程（1）是不適定方程，需要引入正則化因子來求解該不適定方程。根據吉洪諾夫正則化方法選取合適的正則算子和正則參數，通過變分原理，解得不適定方程的正則解［4-5］。

3　三維重力正則化等維反演

3.1模型構制

重力場情況下弗雷德霍姆方程的具體表達式為：

式中：（x，y，z）——整個重力場源區域v內的任意點；

Δρ（x，y，z）——模型在點（x，y，z）處的剩余密度值；

Δg（ξ，η，ζ）——整個重力場源在觀測點（ξ，η，ζ）處產生的重力值；

K——萬有引力常數。

我們構制最小長度解模型，即在方程（1）的約束下，求泛函的極小［7］。

在公式（3）中，ω（x，y，z）為加權函數，可根據先驗信息加大或縮小某部分Δρ（x，y，z）的權重。引入拉格朗日乘數αj（j=1，2，…，N），將上述條件極值問題化為求泛函的極小值的無條件極值問題。

體育教育對于增強青少年身體體質、提高運動技能具有重要作用，作為體育教育的一線工作者，體育教師的能力水平直接影響體育教育質量。然而在學校體育領域，眾多體育教師還保留著傳統的“運動技能中心”和“運動訓練模式”的思維來接受教育培訓，體育教師教育專業化的理念并沒有得到體現[1]。體育教師相較于其他文化課教師而言，其“邊緣化”的地位也是顯而易見的。“同工不同酬”、“由其他任課老師替代”等情況時有發生，其根本原因就是體育教師職業“專業性”的缺失。因此，有必要將體育教師教育放置于一個專業化的框架中進行整體規劃，促進體育教師教育發展，實現國家建立高素質專業化體育教師隊伍的目標。

公式（4）即為反演的目標函數，目標函數的極小值即為所求的模型。

3.2重力場離散模型

通常情況下，地球物理場源是連續的無規則形狀模型，為了方便數值計算，我們需將連續的模型離散成一系列規則模型的組合。

本文采用右手坐標系，x軸垂直于礦體走向，y軸沿著礦體走向，z軸垂直向下。場源網由多個矩形體排列而成，源網的左上角點坐標是（x0，y0，z0）。各單元體的中心坐標是（xk，yl，zm），具有常數密度Δρ（k，l，m）；不同單元體的密度不同（圖1）。

圖1　三維密度場源模型

由于重力場問題是線性的，所以地面觀測點（ξj，ηj，ζj）處的重力異常是所有單元塊體效應之和，公式（1）可以表示為：

其中，（x，y，z）是重力場源區域內的任意點；Δg（ξj，ηj，ζj）是所有單元在觀測點（ξj，ηj，ζj）處產生的重力值之和。

3.3重力核函數

在將場源離散化的過程中，單個塊體的剩余密度值視為常數值，因此，對于單個塊體（圖2），公式（5）可以簡化為：

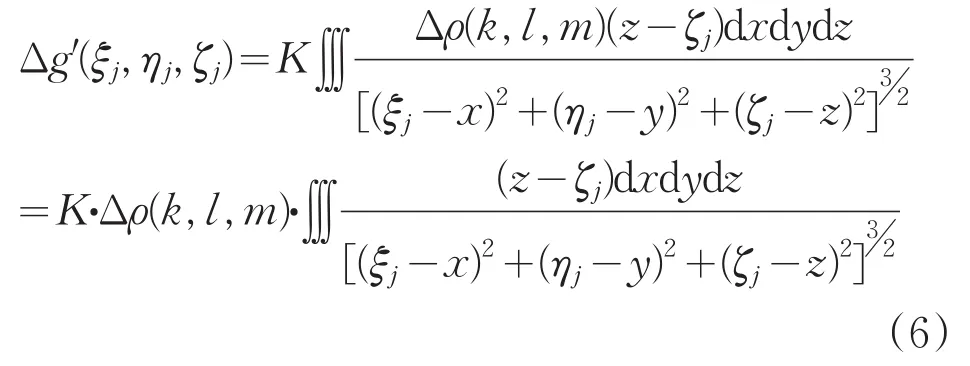
式中的參量含義如圖2所示。其中，（x，y，z）是單元塊體重力場源區域內的任意點；Δg′（ξj，ηj，ζj）是圖中單個場源塊在觀測點（ξj，ηj，ζj）處產生的重力值［2］。

圖2　三維重力核函數中的參量關系

式中：G（j，k，l，m）——重力核函數。

3.4場源分布及質心的確定

根據位場線性反演理論，可以構制模型如下［8］：

其中對稱正定矩陣G的元素是：

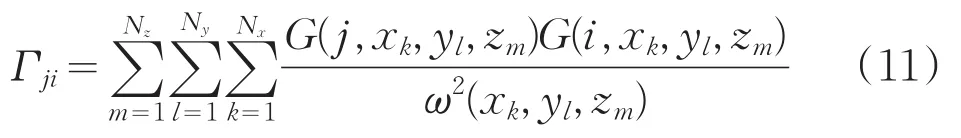
反演求解過程如下：

（1）對重力場根據（8）式計算重力核函數G（j，xk，yl，zm）；

（2）根據（11）式計算內積矩陣Γ；

（3）用正則化方法解方程（10），求得系數向量-→αj；

（4）根據（9）式計算重力場源分布；

（5）計算該重力場源分布所產生的理論重力異常，以便判斷與實際觀測值擬合程度；

（6）計算重力場源質心坐標：

4　結論

針對位場數據反演過程中出現的垂向分辨率低這一問題，在BG理論的基礎上，結合吉洪諾夫正則化方法，給出了用于地球物理位場三維反演的重力異常正則化等維反演方法，詳細介紹了方法的理論基礎及主要公式推導，給出了運用此方法求解地球物理重力場的密度源分布的公式。與傳統位場反演方法相比，正則化等維反演方法參與反演的數據體本身就體現了三維結構，可有效地改善重力位場反演垂向分辨率低的問題。

［1］楊文采.地球物理反演的理論與方法［M］.地質出版社，1996.

［2］劉天佑.重磁異常反演的理論與方法［M］.武漢：中國地質大學出版社，1992.

［3］張貴賓.地磁梯度測深與位場反演［M］.北京：冶金工業出版社，1997.

［4］晉風明.重力異常的正則化等維反演研究［D］.中國地質大學（北京），2008.

［5］盛君.三維重力梯度正反演研究［D］.中國地質大學（北京），2008.

［6］張永明，盛君，張貴賓.航空重力測量技術的現狀及應用［J］.勘探地球物理進展，2006，29（2）：94-97.

［7］張永明，張貴賓，盛君.航空重力梯度測量技術及應用［J］.工程地球物理學報，2006，3（5）：375-380.

［8］王家映.地球物理反演理論［M］.2版.高等教育出版社，2002.

［9］王華嘯.廣義線性反演理論及其在磁異常解釋中的應用［D］.長春地質學院，1985.

P59

A

1004-5716（2016）05-0126-03

2015-12-29

劉堯（1989-），男（漢族），陜西渭南人，現從事地球物理正反演研究及勘探工作。