小波變換在電壓閃變信號中的檢測分析
徐健,邵山
(西安工程大學 電信學院,陜西 西安 710048)
小波變換在電壓閃變信號中的檢測分析
徐健,邵山
(西安工程大學 電信學院,陜西 西安 710048)
為了實現對電力系統中電壓閃變信號更為精確地檢測,提出了小波變換的多分辨率分析的原理。由于小波變換具有較好的時頻局部化特性,進而提取出電壓閃變信號中的頻率和幅值等參數。最后通過MATLAB仿真證明小波變換是一種更為有效的電壓閃變分析方法。
電力系統;電壓閃變;小波變換;多分辨率分析;MATLAB
電壓閃變作為電能質量的重要指標之一,通常是由大功率沖擊性負載的投入所引起的。電壓閃變不僅會引起人的視覺疲勞也會影響到電子儀器、自動控制設備等正常工作[1]。如果能對電力系統中的電壓閃變的信號進行有效的檢測,將會給電壓閃變的治理帶來很大的幫助,對整個電力系統的安全穩定的運行也有十分重要的意義。
隨著電力系統的不斷發展,也逐漸形成了多種對電壓閃變的檢測方法。如傅里葉變換以及 Kalam濾波、最小誤差二乘法、小波變換、S變換等。文中主要介紹前兩種方法及其應用,最后通過對比,小波變換具有良好的時頻局部化特性[2],可以更加方便運用到電壓閃變信號檢測中去。
1 電壓閃變的數學模型
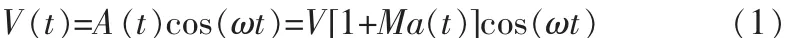
公式(1)中:V(t)是電網電壓的額定值;A(t)為包絡信號;ω代表信號的工頻角頻率;M是調幅系數,M通常為 0.01,最大可取到 0.1;a(t)為調制信號。調制信號表示為
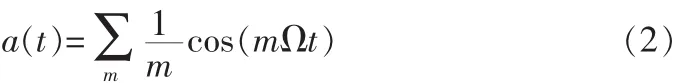
式(2)中,為調制信號的角頻率,代表諧波的次數。
2 分析方法
2.1 傅里葉變換
傅里葉變換是信號分析的最重要的方法,他架起了時域和頻域之間的橋梁。如果周期信號f(t)滿足狄里赫利條件,則的傅里葉級數可表示為:

任何周期函數都可以表示為正弦函和余弦函數的疊加,并且這些正余弦函都是一組正交的函數基[3]。
式(3)中a0為常數分量,an、bn代表頻率分量系數。其中:

傅里葉變換可以將函數f(t)分解為不同頻率的正余弦函數的組合,也說明了傅里葉變換能夠準確地提取出信號的幅頻特性。
2.2 小波變換及其多分辨特性
小波變換的含義是把基本小波的函數ψ(t)做位移τ后,在不同的尺度a下和待分析信號x(t)做內積[4]:

等效的頻域表示為
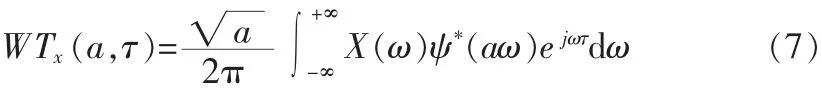
式(7)中,X(ω),ψ(t)分別是x(t),ψ(t)的傅里葉變換。
將任意L2(R)空間中的函數f(t)在小波基下展開,稱這種展開為函數f(t)的連續小波變換(Continue Wavelet Transform),其表達式為:

小波變換也是一種積分變換,Wf(a,b)是小波變換系數,函數 ψ(t)為基小波或母小波[5],a為尺度參數,b為平移參數,基小波波形表現為正負交替兩端振蕩衰減,均值為零。基小波 ψ(t)的傅里葉變換 ψ(w)滿足容許性條件[6]:

小波變換的多分辨率分析將信號在高頻和低頻頻帶上細化,得到越來越精細的時頻描述,可以精確地再現信號在不同層次上的信息,多分辨率分析的方法就是將信號的信息在不同頻帶上體現出來的過程,多分辨率子空間V0可以用有限子空間來逼近[7],即:
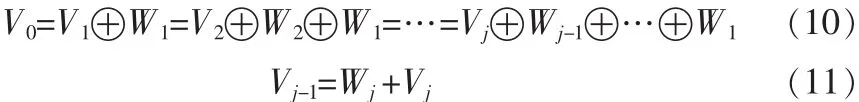
Vj是尺度為j的尺度空間,也是反映空間Vj-1內信號近似部分的低頻子空間;Wj是小波空間,也是反映空間Vj-1內信號細節部分的高頻子空間[8]。Vj和Wj相互正交,從公式(7)又可以看出Wj是Vj在空間中Vj-1的補子空間。
對任意信號f(t)∈L2(R),將其進行多分辨率分解為:

式(12)中:

φj,k(t),ψj,k(t)分別代表尺度函數φ(t)和小波函數ψ(t)經過尺度和位移變化后的函數集合。cj(k)為尺度系數,dj(k)為小波系數。
3 仿真分析
含有突變信號的閃變模型為:
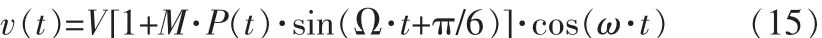

V=1V(標幺值),Ω=14 πrad/s,M=0.04,ω=100 πrad/s采樣頻率為800 Hz,采樣點數為2 000,采樣時間為2.5 s,電壓閃變波形如圖1所示

圖1 含突變信號的閃變波形Fig.1 Flicker mutation signal waveform
經過快速傅里葉(FFT)變換得到的圖形如圖2所示。
圖2 含突變信號的FFT圖形Fig.2 FFT transform graphic of mutation signals
由圖2可以看出FFT只能讀出閃變信號v(t)的幅頻特征,并沒有對閃變信號發生突變的時刻給以精確地區分,因而存在了某種程度的局限性。
根據多分辨率概念,采樣頻率為800 Hz,選用db20小波函數對閃變信號經過第一次分解后得到a1(0~200 Hz)和d1 (200~400 Hz)兩個頻帶。再將a1分解得到a2(0~100 Hz)和d2(100~200 Hz)兩個頻帶。以此類推經過六次分解后得到了a6(0~6.25 Hz)和d6(6.25~12.5 Hz)兩個頻帶,此時7 Hz的閃變頻率就落到了的頻帶上,低頻的頻帶中已經沒有了閃變信號分量,因此多分辨率分解到此為止。a1到a6為信號分解后的各層低頻信號(逼近信號)如圖3,d1到a6為信號分解后的各層高頻信號(細節信號)如圖4。另外在圖4的d1和d2中可以觀察到閃變信號波形有兩個明顯的突變點,分別對應著突變的開始時刻和結束時刻。這就是小波變換優越于傅里葉變換的突出所在。小波變換多分辨率分析能夠將復雜的電壓閃變信號頻率劃分到各子頻帶中,特別適合于調幅波中混合多種頻率成分的情況。這是小波的多分辨率特性在電壓閃變信號分析中的價值的最要的體現。
4 結束語
通過對閃變信號的仿真將傅里葉變換和小波變換的不同特點體現出來,仿真分析的結果可以看出小波變換在電壓閃變信號的時頻分析方面比傅里葉變換具有更強的分析能力。而快速傅里葉變換分析信號時只能反應頻域上的信息,對時域不能做出任何的識別分析能力。小波的多分辨特性能將電壓閃變不同頻率的信號分離,從而能觀察到信號的細微變化,也可以觀察出突變的開始和結束時刻,因此小波變換換更適用于對電壓閃變信號的分析。小波變換為我們的電壓閃變檢測工作提供很有價值的信息,對后續閃變問題的治理也具有十分重要的實際意義。
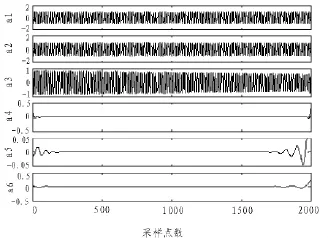
圖3 信號v(t)小波分解后各層逼近信號Fig.3 Approximate components on each floor after the wavelet transform

圖4 信號v(t)小波分解后各層細節信號Fig.4 Detailed components on each floor after the wavelet transform
[1]劉會金,吳玉蓉,熊玲玲.基于Daubechies小波的多分辨分解在電壓閃變信號分析中的應用[J].繼電器,2004,32(13): 6-10.
[2]張勇,管聲啟.基于小波提升分解的帶鋼表面缺陷檢測[J].西安工程大學學報,2013(4):1-2.
[3]謝小磊.電壓波動與閃變的小波分析[D].南京:河海大學,2006.
[4]郭曉麗,朱志松,許小梅.短時間閃變嚴重度Pst的計算方法的研究[J].南通工學院學報:自然科學版,2004,3(3): 66-69.
[5]郝曉平,黨幼云.基于FPGA的信號奇異性檢測[J].西安工程大學學報,2011(6):1-2.
[6]Dwight F M,Kraig J.OLEJNIZAK.小波基礎及應用教程[M].楊志華,楊力華譯.北京:機械工業出版社,2006.
[7]張志剛.電能質量講座 第八講電壓波動與閃變[J].低壓電器,2007(16):56-60.
[8]桑松,柴玉華,孫影.基于小波變換和快速傅里葉變換的諧波檢測[J].電測與儀表,2012,49(559):29-32.
[9]任震,黃群古,黃雯瑩.多層多分辨分析算法及在電力系統中的應用[J].電網技術,2012(6):5-7.
Detection and analysis of wavelet transform in voltage flicker signal
XU Jian,SHAO Shan
(College of Electronic Information of Xi’an Polytechnic University,Xi’an 710048,China)
In order to more accurately detect the power system voltage flicker signal,,this paper proposes the principles of multi-resolution wavelet analysis.Wavelet transform has good time-frequency localization properties and then extract the voltage flicker signal parameters such as frequency and amplitude.Finally through MATLAB simulation,it is proved that the wavelet transform is more effective in analysis of voltage flicker.
power system;Voltage Flicker;Wavelet transform;Multi-resolution analysis;MATLAB
TP
A
1674-6236(2016)04-0155-03
2015-04-14 稿件編號:201504139
陜西省教育廳專項科研計劃(2013JK1015)
徐 健(1963—),男,陜西西安人,碩士,副教授。研究方向:電能質量檢測、信號與系統等。

