經歷定義過程 理解概念本質

嚴政建

在教學“圓的認識”這一課時，很多教師會把圓的概念、半徑、直徑及其關系作為教學的重點，會選擇折一折、比一比、量一量的方式進行數學活動，用告訴、發現的方式讓學生認識這些概念；在教學用圓規畫圓時會總結詳細的畫圓步驟，讓每位學生掌握畫圓的方法；在滲透數學文化時，會非常重視數學知識的人文背景，向學生充分展示圓的文化內涵，但在基本的數學知識與數學能力方面，學生沒有達到數學的理性與概括。綜觀這樣的獲得知識，除了豐富學生的知識儲備、搭建必要的認知臺階外，并沒有為學生數學思考力的提升作出貢獻。因此，對圓概念的本質理解是不深入的，學生心中呈現的仍然是一個靜態的圓。如何讓學生心中的圓動態化，筆者認為，教師在教學圓這個概念時不應該只是為了定義而教學，而應該讓學生經歷定義化過程。于是筆者進行了以下幾個教學片段的嘗試，收到了較好的效果。

一、從“圓規”到“直尺”——突破畫圓工具，理解圓的內涵

學生對圓既熟悉又陌生，一方面學生已經知道了圓的形狀特征（半徑、直徑及關系等），另一方面對圓的圖形性質（到定點距離等于定長）又知之甚少。用圓規畫圓是為了讓學生掌握圓的一些基本知識，通過動手操作讓學生發現圓的特征之間的關系，同時也歸納出畫圓的方法的兩個要點：定點和定長。但是在這個操作活動中思辨活動比較少，也就是說畫圓為什么要定點、定長，這個概念學生是模糊的。因此在學生掌握了用圓規畫圓后再提出一個思維挑戰：用直尺畫圓。用直尺畫圓，先讓學生定點，然后思考定長。怎么定長是考驗學生的關鍵問題，學生必定會思考怎么才能使從定點出發的線段相等。通過實踐學生想出了五種方法，讓學生在思辨中感悟到圓的本質屬性——到定點距離等于定長。因此，用概念的本質去解決畫圓的方法才是解決一切問題的法寶。

師：你能用圓規畫圓嗎？請你試著畫一個圓，畫圓時想一想要注意什么呢？（生畫圓）

師：說一說畫圓時要注意什么。

生：圓規兩腳分開。

生：圓規兩腳之間的高度要一樣。

生：畫圓的過程中圓規要稍微傾斜30度左右，使畫出的圓的線條流暢，畫圓過程中帶有針的一端不能移動。

生：圓規兩腳的距離不能改變。

師：圓規兩腳的距離為什么不能動？

生：動了就是一個腳到圓心的距離不相等了。

生：動了半徑就不一樣了。

……

師：聽了剛才同學們說的注意點，我認為有兩點很重要：（1）找一個合適的地方，定點；（2）圓規兩腳之間要有一定的距離，定長。

師：按照同學們說的，老師也來畫一個（邊說邊畫），先定點，再定長。

師：請你把剛才畫的圓修正一下，或重畫一個。

……

師：剛才我們用了圓規，先定點再定長畫了一個圓，你能不能用直尺，利用定點、定長這兩個知識點畫一個圓呢？你打算怎么畫？小組討論下。

方法一：

生：我們組的辦法是先在紙上定一個點，然后從這個點出發畫3cm長的線段，畫得越多越好，然后把各條線段的另一端點用曲線連起來。

師：畫得越多越好是什么意思？

生：因為圓的半徑都相等的，其實這些線段就是圓的半徑，半徑可以畫無數條，畫得越多曲線就容易連起來。

方法二：

生：我們跟他們不一樣。先畫一條10cm的線段，取一個中點，再通過中點畫20條10cm的線段，并且這個點都是這些線段的中點。然后把這些線段的端點用曲線連接起來。

師：你的定點、定長在哪里？

生：定點其實是這個中點，定長是10cm線段的一半5cm。

師：為什么要畫20條這樣的線段呢？

生：線段畫得越多越好，曲線就容易連接起來，不一定要20條，30條、40條都可以。

方法三：

生：先畫一個十字架，每條線段定一個點到中點的距離相等，然后把4個點用曲線連接起來。

師：……

方法四：

生：用一把直尺量取一段長度作為圓的直徑，記錄下這條線段的中點，把這個中點作為圓的圓心，把直徑作為邊長作一個正方形，然后作這樣無數個正方形，這樣正方形的頂點就會構成一個圓的圖形，這個我是在一本書上看到的。

方法五：

生：畫一個正六邊形，然后把多邊形的頂點用弧線連起來。

……

師：你們的方法太好了，用直尺也能畫圓。那讓我們一起來用直尺畫圓吧。

二、從“小”到“大”——突破空間的局限，體驗圓的特征

如果說用圓規畫小圓、等圓是讓學生感受畫大小不同的圓是跟定長有關，那么讓學生在操場上思考怎樣畫大圓是為了進一步讓學生體會，畫圓不一定要用圓規，只要有定點與定長就可以，這也是對用直尺畫圓的突破。因此，在教學中發現有學生用“十字坐標”法畫圓，這種方法其實是對直尺畫圓的一種遷移。而學生想到了用釘子與繩子畫圓的方法是一種對圓定義的突破。只要將與圓心距離處處相等的點連起來就成圓了，可以進一步體會到圓的特征。因此，這樣教學學生對數學知識的獲取，不是被動地接受，而是一種自我建構數學知識的過程。

師：剛才我們用圓規、直尺在紙上畫圓。老師這里有一個半徑為4cm的圓，你能跟我畫一個同樣大的圓嗎？想一想應該怎么畫？

生：只要我畫的圓半徑定在4cm就行了。

生：……

師：請你在紙上畫一個與老師的圓一樣大的圓。（生畫圓）

師：剛才我們都是在紙上畫一些小圓，如果要在我們的操場上畫一個半徑為2.5米的大圓，你有沒有好方法？（生思考）

師（啟發）：我們的圓規比較小、直尺比較短，籃球場上畫大圓還能用它們來畫嗎？

生：不行。

師：那我們的定點、定長怎么辦呢？

生：我們可以用一根2.5米長的繩子，固定一端，然后以另一端繞著這個端點轉一周就成了一個大圓。

生：還可以先在操場上畫十字坐標，以十字坐標的交叉點為圓心，定好上下和左右的半徑，畫出一個正方形。然后再連接它們的對角線，采用切割的方法，先把正方形切成正8邊形，再切成正16邊形，再切成正32邊形。然后把各個點連接起來就成圓了。

三、從“方”到“圓”——突破思維限制，感悟圓的本質

“一中同長”是圓和其他平面圖形的本質特征得以凸顯與內化的重要屬性，而“曲線圖形”“沒有角”等特點是圓的非本質屬性。從中心到圖形上相等的線段條數的對比教學，一方面深化了學生對多邊形特征的認識，另一方面更是在比較辨析中促成了學生對圓的半徑有無數條、所有的半徑都相等的深層次認同。從正六邊形一直到正800邊形，更是架起了多邊形與圓之間的橋梁，讓學生有了直與曲圖形辯證統一、有限與無限、量變與質變等的思考。

師：同學們，我們以前認識圖形特征就是從邊和角兩個方面來研究的，圓確實具有大家說的這些特點。知道古人是怎么說圓的特征嗎？

師：古人說圓是“一中同長”，明白這句話的意思嗎？

生：一個中心點！

師（笑著）：什么是“同長”？

生：半徑一樣長，直徑的長度也一樣長。

師（反問）：圓，有這個特征嗎？

生（齊聲）：是的。

師：在正三角形、正方形、正五邊形、正六邊形中“一中不同長”嗎？（如下圖）

生：如果把線連到三角形的邊上，那么它們線段的長度就是不一樣的。

師：連在各頂點上的長度是相等的，但連接邊上的長度與連接頂點長度就不一樣了（出示課件），但是圓呢？

生：都一樣。

師：是的，圓上的點到圓心的距離都是相等的，而且正三角形內，中心到頂點有3條線段相等，正方形有4條，正五邊形有5條……圓呢？

生：有無數條。

師：為什么是無數條？

生：因為圓上面有無數個點。

師：那誰來說說，半徑是一條怎樣的線段？

生：一端在圓心，一端是圓上任意的一個點。

師：其實，圓出于方。（課件演示正多邊形邊數不斷增多，最后轉變成圓的動態過程）

生（驚奇）：成一個圓了！

師：現在是正800邊形！

師：看到這里你有什么想法？

生：圓是正多邊形變成的。

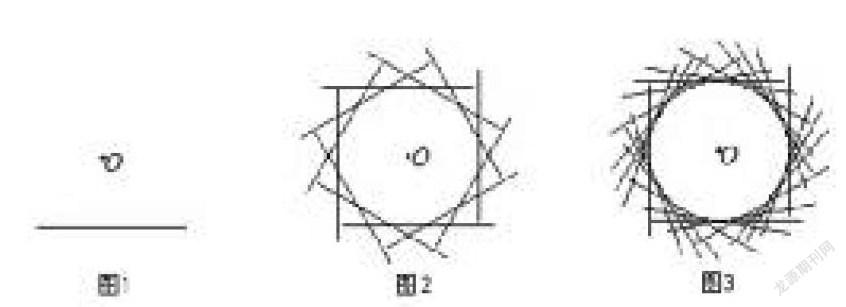
生：我認為圓是一個正無數邊形。

生：圓可以想象成正無數邊形。

師：你們說得太好了。現在請你閉眼想一想，當這個正多邊形的邊數越來越多的時候，這個正多邊形會接近什么圖形？

生：圓。

師：用老子的話來說就是“大方無隅”。大方就是指最大最大的方，“無隅”猜一猜，“隅”是什么意思？

生：角。

師：這樣一來，圓是不是“一中同長”。

生：是的。

師：是的，圓“一中同長”才是它的本質特征，在我國古代的時候墨子就發現了，比西方早了1000多年……

通過三個環節對圓概念特征的體驗，學生以思辨的形式對“圓為什么會圓”這個問題進行了反復理解，使其明白了“圓是到定點的距離等于定長的點的軌跡”真正的意義。因此，對圓概念的教學應該讓學生經歷定義的過程。

（浙江省杭州市大關苑第一小學 310014）