把散落的“珍珠”串成美麗的“項鏈”

【摘 要】正方形集中了矩形菱形的所有性質，而兩個完全相同的正方形疊合在一起旋轉，不僅會產(chǎn)生疊加的結論，還能把正方形的性質、三角形全等、相似以及重疊部分面積、函數(shù)等核心知識串起來，既體現(xiàn)問題的基礎性也彰顯問題的綜合性，這樣的專題復習課更有利于學生數(shù)學思維能力的發(fā)展。

【關鍵詞】正方形;旋轉;核心知識;專題復習

【中圖分類號】G633.6 ?【文獻標志碼】A ?【文章編號】1005-6009（2016）03-0032-04

【作者簡介】章曉東，江蘇省無錫市甘露學校（江蘇無錫，214117）校長，江蘇省特級教師，江蘇省首批基礎教育課程改革先進個人，江蘇省教師培訓中心“送培到市縣”專家組成員，常熟理工學院繼續(xù)教育學院兼職教授。

【主題概述】

通過本課的學習，學生能夠進一步體悟解決雙正方形旋轉問題的核心知識點是旋轉的性質、正方形的性質、三角形全等與相似。同時，還要讓學生通過雙正方形的旋轉領悟旋轉過程中的變與不變，變就有可能存在函數(shù)關系，不變就可能存在相等（定值）、全等或相似關系，這就是雙正方形旋轉問題展現(xiàn)給學生的數(shù)學本質的魅力，也是數(shù)學所特有的哲學價值。

解決旋轉問題的基本策略是“化靜為動，以靜制動”。所謂“化靜為動”，即要搞清楚整個旋轉過程中哪些元素（如邊、角）發(fā)生了變化，哪些元素仍然沒變，有時還要通過特殊位置圖形的特征來判斷不變的元素。所謂“以靜制動”，即要把旋轉過程中的各種圖形的位置情況作為靜止的圖形進行研究，接下來的計算與證明和原先步驟一致，只不過賦予了旋轉的背景而已。如果學生能夠破譯旋轉背后的“密碼”，那么以旋轉為背景的幾何問題就迎刃而解了。

【課堂教學實錄】

一、激活

師：熟悉正方形嗎？誰來說說對它的認識。

生1：正方形四個角都是直角，四條邊相等且對邊平行，對角線相等且互相垂直平分，每條對角線平分一組對角。

生2：正方形既是軸對稱圖形又是中心對稱圖形。

師：很好。是的，正方形集中了矩形和菱形的所有性質。那么，如果兩個完全相同的正方形疊合在一起旋轉，會產(chǎn)生哪些疊加的結論呢？這就是我們今天要研究的課題“旋轉所鐘情的雙正方形”。大家是否留意今天老師發(fā)給大家的作業(yè)單上的例題和你們平時見到的例題有什么不同呢？

生眾：只有條件，沒有問題。

師：那問題（結論）讓大家來猜想如何？有沒有信心自己來編題？

生眾：有（聲音響亮）。

【設計意圖】激活的意義在于激活情感，激活舊知，激活思維。紐帶是激活情感，基礎是激活舊知，根本是激活思維。對正方形性質的回顧與熟悉，是解決以旋轉為背景的雙正方形問題的核心知識點之一。

二、生長

教師打開幾何畫板課件。

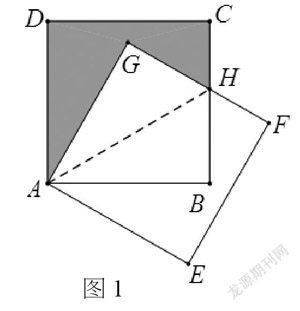
例題1：如圖1所示，把正方形ABCD繞著點A按順時針方向旋轉α（0°≤α≤90°）得到正方形AEFG，F(xiàn)G與BC交于點H。

師：一般我們可以從哪幾個方面來提問題（猜想）呢？

生3：線段、角、面積。

師：那我們就先從簡單的線段、角等方面來猜想問題（結論）。

生4：可以猜想GH=HB，HF=HC。

師：誰來證明生4的猜想？李老師，你到上面來和同學們講（教師請舉手的“李”姓學生上屏幕前來講，學生們發(fā)出會心的笑聲）。

生5：連接AH，……只需證明△AGH≌△ABH即可。

師：老師也來提個問題，若AD=3，∠DAG=30°，你能求出陰影部分的面積嗎？大家先試試看。

教師巡視，發(fā)現(xiàn)部分學生設法把陰影部分面積割成矩形、直角三角形或直角梯形來做，但找不到突破口（請一“王”姓學生到屏幕前講解）。

生6：陰影部分的面積等于正方形面積減去四邊形GABH的面積，而四邊形GABH的面積等于△ABH的面積的2倍。根據(jù)剛才證明的△AGH≌△ABH，故∠GAH=∠BAH=30°，利用解直角三角形的知識求得S△AGH=S△ABH=，因而陰影部分的面積為9-3。

師：非常好。同學們，王老師此題的解決過程給你們什么啟發(fā)？

生7：解題時要懂得以退為進。當面積“割”不行時，我們要想到面積的“補”。

師：“割”時“山重水復疑無路”，“補”時“柳暗花明又一村”。請同學來小結一下，解決此題的核心知識是什么？

生8：正方形的性質，全等三角形的判定，面積的割補。

……

【設計意圖】“教學即生長”。這個題目的設計基于三點考慮，一是引導學生通過觀察圖形嘗試提出一些簡單的問題，激發(fā)他們會猜想、敢提問、能提問的積極性;二是“起點低”，讓基礎一般的學生也能夠通過全等三角形來證明簡單的問題（如線段相等）;三是通過教師提問，讓問題有一定的挑戰(zhàn)性，逐級遞進，不斷“生長”，符合學生的認知特點。

三、啟智

例題2：如圖2所示，正方形ABCD與OEFG都是邊長為4的正方形，其中點O為正方形ABCD的對角線AC的中點，正方形OEFG繞點O順時針旋轉α（0°≤α≤90°）。

師：在旋轉的過程中，試猜想圖2中有哪些結論？

生9：CM=BN，BM=AN，OM=ON，MG=NE。

生10：兩個正方形重疊部分的面積是定值。

師：這位同學有“火眼金睛”哦。說說你是怎樣來猜想的？

生10：只要把正方形GOEF繞O點逆時針旋轉，使得M與C重合，則重疊部分面積等于△BOC的面積。（教師運用幾何畫板的旋轉功能進行演示）

師（豎起大拇指）：從特殊位置入手來猜想，真牛！

師：下面先請趙老師來說怎么來證明生9的猜想（教師點名舉手的“趙”姓學生到屏幕前講解）。

生11：連接OC、OB，構造全等三角形，……證明△COM≌△BON。

師：兩個正方形重疊部分的面積是定值，能求嗎？請張老師來說。（教師點名舉手的“張”姓學生到屏幕前講解）

生12：還是要用到剛才的全等三角形。由△COM≌△BON可知S陰影=S△BON+S△BOM=S△COM+S△BOM=S△BOC=S正方形ABCD=4。

師：老師也想提個有挑戰(zhàn)性的問題，設CM=x，△MON的面積為y，試寫出y與x的函數(shù)關系式。（教師問學生是否有信心，學生大聲回答有。）……請陳老師來說。（5分鐘后，教師點名舉手的“陳”姓學生到屏幕前講解）

生13：由剛才的兩個結論可知，CM=BN=x及BM+BN=4可得BM=4-x，故y=S△MON=S重疊-S△BMN=4-x（4-x）=x2-2x+4。

師：很不錯。同學們，此題的解答過程又給你們什么啟發(fā)？

生14：雖然圖形在變化，但解決問題的關鍵還是全等三角形與面積割補。

師：真不錯。“是他，是他，還是他”。（歌詞惹笑了學生）能否直接求S△MON？請同學們課后思考。

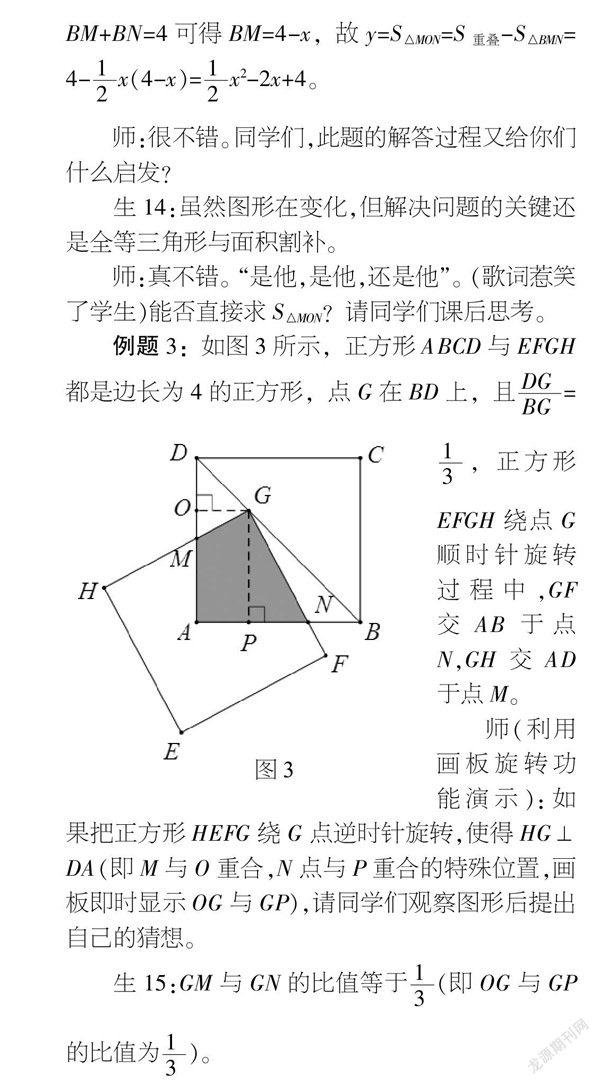
例題3：如圖3所示，正方形ABCD與EFGH都是邊長為4的正方形，點G在BD上，且=，正方形EFGH繞點G順時針旋轉過程中，GF交AB于點N，GH交AD于點M。

師（利用畫板旋轉功能演示）：如果把正方形HEFG繞G點逆時針旋轉，使得HG⊥DA（即M與O重合，N點與P重合的特殊位置，畫板即時顯示OG與GP），請同學們觀察圖形后提出自己的猜想。

生15：GM與GN的比值等于（即OG與GP的比值為）。

生16：重疊部分（即矩形OGPA）的面積等于3。

師：怎么證明這兩個猜想？請錢老師來講（教師點名舉手的“錢”姓學生來屏幕前講）

生17：只要證明兩個等腰直角△DOG與△GPB相似即可……

師：如果再旋轉到一般情況，原來的結論還成立嗎？（利用畫板旋轉功能演示原先的一般位置，顯示的是M、N兩點，O、P兩點自動隱去）

有學生說成立，有學生說不成立，也有學生無法確定。

師：我們不妨先來研究GM與GN的比值是否等于？請孫老師來講（教師點名舉手的“孫”姓學生來屏幕前講）

生18：還是要作出剛才的矩形OGPA，已經(jīng)證明兩個等腰直角△DOG與△GPB相似，只要再證明△GOM∽△GPN，從而轉化為求剛才的矩形兩邊之比為。

師：重疊部分（即四邊形MGNA）的面積會是定值3嗎？

生19：不會，因為△GOM和△GPN只會相似，不會全等，所以，通過面積割補沒法拼成原來的矩形面積。

師：非常好。那如果設BN=x，重疊部分（即四邊形MGNA）的面積為y，你能求出y與x的函數(shù)關系式嗎？請大家先動手試試看。

師：請劉老師來講。（教師點名舉手的“劉”姓學生來屏幕前講）

生20：重疊部分面積可以分割成直角梯形與直角三角形的面積。易求DO=OG=1，GP=PB=3，設BN=x，則PN=3-x，利用△GOM∽△GPN求出OM=（3-x），于是AM=3-（3-x）=2+x。∴y=（2+x+3）+×3×（3-x）=7-x。

師：真厲害。還可以怎樣分割？

生21：連接AG，把重疊部分面積分割成兩個三角形面積，同樣可以求出……

師：真好！那請你再來說說，解決此題的核心知識是什么？

生21：相似三角形的判定和面積的割補。

【設計意圖】啟智即啟發(fā)學生智慧。數(shù)學教學是基于活動的教學，在數(shù)學探究活動過程中，要注重讓學生“感受過程，習得規(guī)律，啟發(fā)智慧”。核心知識從全等過渡到相似，數(shù)學思想從特殊到一般，學生不斷經(jīng)歷認知沖突，不斷迸發(fā)智慧火花。

四、生慧

師：請同學們來談談，通過本課的學習，你們有哪些收獲和體會？

生22：在旋轉過程中，常常會用到全等相似的知識。圖形變化，但方法不變。（教師板書：全等相似）

生23：對于面積問題，不僅要會“割”，也要學會“補”，解題中要“以退為進”。（教師板書：以退為進）

生24：旋轉問題要多從特殊和一般兩個方面去思考，去轉化。（教師板書：轉化）

師：總結得太精彩了！Wonderful！同學們已經(jīng)把老師想說的話都說完了（學生笑）。我嘗試把同學們的總結串起來編成一首詩。“旋轉全等相似，割補可解謎盤;困時以退為進，特殊轉化一般。”（掌聲）兩個完全相同的正方形疊合在一起旋轉，果然產(chǎn)生了疊加的美麗結論，這就解釋了今天的學習主題“旋轉所鐘情的雙正方形”的魅力所在。課后請同學們思考，如果把兩個正方形的旋轉換成兩個矩形的旋轉，又會有什么結論？

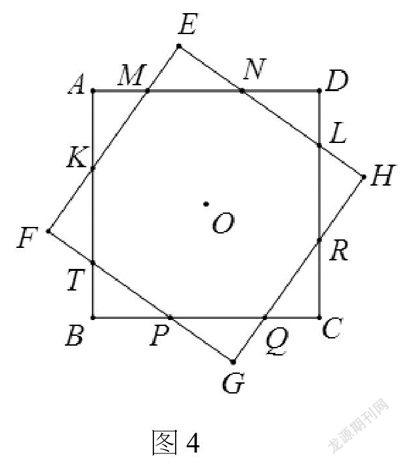
課后拓展：如圖4所示，將兩張互相重合的正方形紙片ABCD和EFGH的中心O用圖釘固定住，保持正方形ABCD不動，逆時針旋轉正方形EFGH。

（1）試給出旋轉角度小于90°時的一些猜想：①ME=MA;②兩張正方形紙片的重疊部分的面積為定值;③∠MON保持45°不變。

請你對這三個猜想作出判斷（正確的打上“√”，錯誤的打上“×”）。

（2）可以發(fā)現(xiàn)：（1）中的△EMN的面積S隨著旋轉角度∠DOE的變化而變化。請你指出在怎樣的位置時△EMN的面積S取得最大值。（不必證明）

（3）上面的三個猜想中若有正確的，請選擇其中的一個給予證明;若都是錯誤的，請選擇其一說明理由。

【設計意圖】“生慧即生成”。課后拓展的目的就是為了打破學生慣用全等的思維定勢，讓學生明白，研究數(shù)學問題既要基于定勢又不能囿于定勢思維，要能夠以退為進，靈活運用。生慧這一環(huán)節(jié)也是數(shù)學知識的反饋鞏固過程，生成新的探究問題的過程，生成數(shù)學方法與思想的過程，生成學生智慧的過程。

【課堂感悟】

本節(jié)課是初三專題復習課，針對不同學習層次的學生展開教學過程的設計，體現(xiàn)“起點低（注重基礎，下要保底），步子緊（小步子式逐步提高要求），落點高（上不封頂）”的設計要求，利用幾何畫板的動畫功能演繹旋轉過程中的變與不變。

本節(jié)課共設計了4道例題，足夠供學生課內(nèi)外的訓練和思考了。每道例題的設計都是安排兩個完全相同的正方形旋轉，這樣做的目的一方面因其旋轉要素已經(jīng)涵蓋了圖形旋轉的類型和特征，另一方面是因為正方形是四邊形中最特殊的四邊形，它集中了矩形和菱形的所有性質，兩個完全相同的正方形通過旋轉會產(chǎn)生性質疊加，不僅結論會更加豐富多彩，而且解決問題的方法也是多樣化的，從而使得旋轉變換更具魅力。

每道例題的內(nèi)部都以問題串的形式出現(xiàn)，而4道例題本身，前一題都是后一題的基礎與鋪墊，后一題都是前一題的提升和拓展，我中有你，你中有我，這就構成了“套題（題組）”式訓練方式。復習課如果堅持這樣去做，學生才能真正“聰明”起來，才能真正達到“以少勝多”的最大功效，才能讓散落的“珍珠”（零散的知識點）串成美麗的“項鏈”（內(nèi)化的知識結構和學生內(nèi)生的智慧）。可見，教師組織教學內(nèi)容要突出其與其他的數(shù)學知識和方法間的縱向與橫向聯(lián)系。一個數(shù)學知識與其他數(shù)學知識的聯(lián)系越多，說明該知識越重要，它的拓展性就越強。

值得課后進一步思考的問題有：如果把4道例題放在直角坐標系的背景中，知識的綜合程度就更高，但不宜作為第一輪復習的要求。如果把其中一個正方形縮小一半，題目的結論會有怎樣的變化？如果把其中一個正方形換成矩形情況又該如何？如果兩個正方形都換成矩形又該是怎樣的結果？如果把兩個正方形都換成正六邊形結果又該如何呢？等等。在這類問題的教學中一定要以數(shù)學知識為載體，切忌“空對空”，要多讓學生去想，去悟，這樣才能取得理想的效果。