Temperature Compensation Algorithm Based on Least Squares Curve Fitting in Flow Measurement*

SHAO Xianhe，LU Zhicheng，WANG Zhu（Harbin Institute of Technology at Weihai，School of Information and Electrical Engineering，Weihai Shandong 264209，China）

?

Temperature Compensation Algorithm Based on Least Squares Curve Fitting in Flow Measurement*

SHAO Xianhe*，LU Zhicheng，WANG Zhu
（Harbin Institute of Technology at Weihai，School of Information and Electrical Engineering，Weihai Shandong 264209，China）

There are serious non-linear errors in flow measurement of ultrasonic heat meter utilizing time difference method.This paper gives detailed calculation and analysis to explain that the errors are caused by the changes of flu?id temperature.To solve this problem，a temperature compensation algorithm based on least squares curve fitting is proposed.Temperature compensation is realized through establishing a non-linear mapping model between flow rate and fluid temperature.However，each meter has different metrological properties.So this paper puts forward an er?ror second-order correction algorithm further.The error of flow rate at current temperature is calculated according to the errors at two adjacent temperature spots and variable weight.The flow measurement global optimization is real?ized by second-order correction.Experimental verification showed that flow measurement error was between±2.0%. So this algorithm has definite value to engineering application.

ultrasonic heat meter；flow measurement；temperature compensation；least squares surface fitting；error correction

時差法超聲波式熱量表是通過測量超聲波順、逆兩向的時間差計算流量，然后代入焓差法或K系數法公式計算出熱量［1］。流量計量的精確度直接決定著熱量計量的精確度［2］。超聲波式熱量表通常工作在30℃～80℃的環境下。而超聲波在水中的傳播速度隨溫度呈非線性變化，從而給流量計量帶來非線性誤差。因此，在用超聲波進行流量計量時，必須要考慮溫度對超聲波傳播速度的影響。同時，溫度變化還會對管道內流體的流動形態產生影響。目前，超聲波式熱量表多采用查表法進行溫度補償。查表法速度快，但是數據量大，對單片機的存儲容量要求高，而且只能實現局部最優。文獻［3］通過建模仿真和現場實驗，提出了基于BP神經網絡的溫度補償算法，補償效果較好，但是選取的樣本點（溫度和流量）少，而且沒有考慮超聲波式熱量表自身計量特性的差異，不能進行二次修正，因此不適合在實際生產中推廣應用。

針對上述問題，通過分析溫度對時差法流量計量精確度的影響，提出了基于最小二乘曲面擬合的溫度補償算法和多溫度點誤差二次修正算法，不僅實現了對流量計量的溫度補償，而且可以對溫度補償后的每塊超聲波式熱量表進行誤差二次修正，提高了流量計量的精確度和穩定性，可在工業生產中推廣應用。

1　時差法超聲波式熱量表流量計量誤差分析

1.1時差法流量測量原理

U型聲道時差法流量測量管道結構如圖1所示［4］。

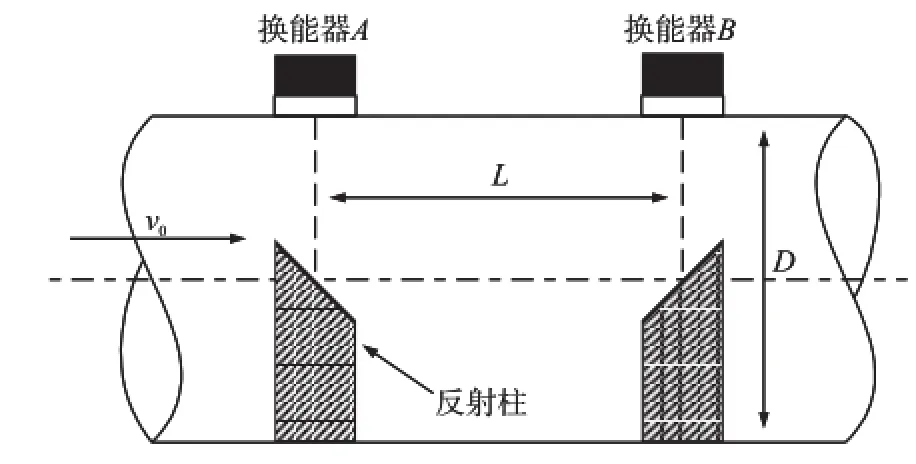
圖1　U型聲道時差法流量測量原理示意圖

換能器A和B分別安裝在管道上游和下游，間距為L。A和B交替收發超聲波信號實現時間差的測量。假設管道內徑為D，流體流速為v0，流體靜止時超聲波在流體中傳播的波速為c。當超聲波順流傳播時，超聲波從發射端發出經反射柱兩次反射到達接收端的時間為t1。逆流傳播時，從發射端到達接收端的時間為t2。反射柱為不銹鋼材料，會改變原有的流速分布。但是，安裝反射柱后的流速分布場是確定的，可以根據其分布進行流速補償。而且通過反射柱可以增加超聲波傳播距離、增大傳播時間差減小流速測量誤差。

由時差法原理可知流體體積流量V為：

式中，K為流速修正系數，可根據流體的流動形態確定。

1.2溫度對超聲波傳播速度的影響

由式（1）可知，流體的體積流量與超聲波傳播速度的平方呈線性關系。而超聲波傳播速度隨溫度呈非線性變化［5］，其變化趨勢如圖2所示。

若僅考慮超聲波傳播速度對流體體積計量結果的影響，則式（1）可簡化為：

假設在程序中使用超聲波在74℃的流體中的傳播速度（1 555.47 m/s）計算流體體積，而當流體真實溫度為30℃時，超聲波在流體中傳播的波速為1 509.44 m/s。則流體體積流量計量誤差為：

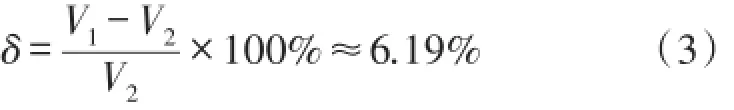
式中，V1為使用超聲波在74℃的流體中的傳播速度計算得到的流體體積流量，V2為使用超聲波在30℃的流體中的傳播速度計算得到的流體體積流量。

對于高精確度的流量測量，這個誤差是不可忽略的。

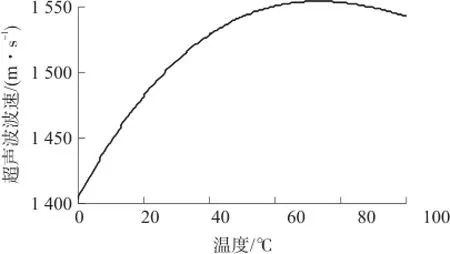
圖2　超聲波傳播速度隨溫度變化圖

1.3溫度對管道內流體流動形態的影響

管道內流體因粘滯性而具有兩種流動形態：層流和紊流。液體質點作有條不紊的運動，彼此不相摻雜的形態稱為層流。液體質點作不規則運動、互相混摻、軌跡曲折混亂的形態稱為紊流［6］。

圖3為層流與紊流流速分布圖。兩種流動形態下管道軸心線流速與面流速之間的關系分別為：

層流：K=v/v0=0.5

紊流：K=v/v0=0.75～0.9（為簡化計算，一般取0.825。由此帶來的誤差可通過溫度補償消除）

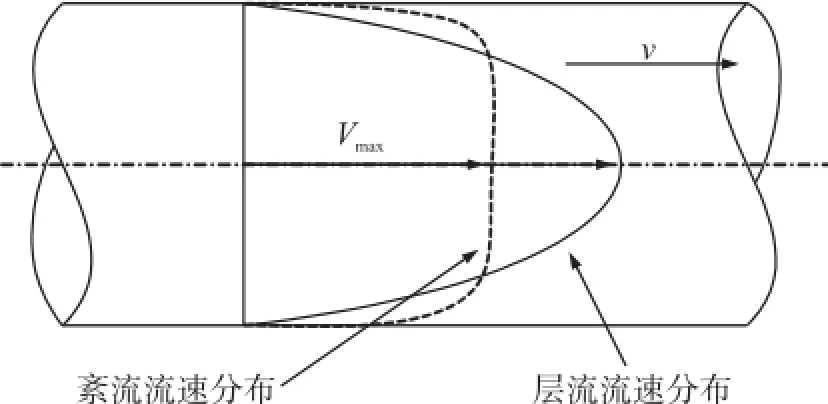
圖3　層流與紊流流速分布

流體的流動形態可由雷諾數Re判別。在工程計算中，當Re≤2 000時是層流；當Re＞2 000時是紊流。對于圓形截面管道，雷諾數Re可由下式計算：

式中，vˉ為管道內流體的平均流速；d為管道內徑；υ為流體的運動粘度。由于流體的運動粘度與溫度存在非線性關系。因此，當管道內流體流速和管徑恒定時，雷諾數Re的值隨溫度呈非線性變化［7］。

假設D=20 mm，vˉ為0.05 m/s，流體溫度為30℃，運動粘度υ為8.009×10-7m2/s［8］。按式（4）計算得Re為1 248.60，流體的流動形態為層流。流速修正系數K取0.5。當溫度升高到80℃時，運動粘度υ為3.650×10-7m2/s，計算得Re為2 739.73，流體的流動形態為紊流。流速修正系數K取0.825。則流體體積流量計量誤差為：

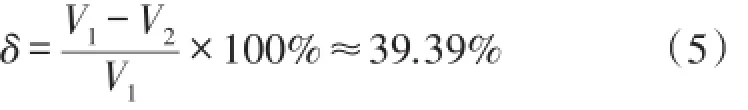
式中，V1為流體溫度為80℃時的流體體積流量，V2為流體溫度為30℃時的流體體積流量。

管道內流體的分布規律極為復雜。為了計算方便，通常認為超聲波式熱量表在全量程內始終工作在一種狀態，在計算流量時流速修正系數K取固定值。但是，當溫度變化時，管道內流體的流動形態可能會改變，給流體體積計量帶來較大誤差。

由上述分析可知，溫度對超聲波流量計量的精確度有著不可忽視的影響。在高精確度的流量計量中，必須要進行溫度補償。

2　最小二乘曲面擬合原理

2.1曲面模型的選擇

對同一組采樣數據，不同的曲面模型擬合效果存在較大差異。我們可以通過以下參數來評價各曲面的擬合效果，從而選擇最佳擬合曲面模型。

SSE（誤差平方和）：曲面預測值和采樣值的誤差平方和。

RMSE（均方根誤差）：曲面預測值和采樣值的誤差均方根。

R-square（確定系數）：曲面預測值和采樣數據均值之差的平方和與采樣值和采樣數據均值之差的平方和的比值。

當SSE和RMSE越小，R-square越接近1時，曲面模型的擬合效果越好［9］。

2.2曲面方程的求解

通過比較多項式逼近和指數逼近的擬合效果，最終選擇二元二次多項式作為擬合曲面模型，其規范化表達式為：

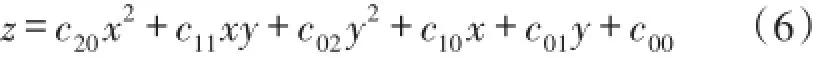
式中，x，y，z是采集的數據，c20，c11，c02，c10，c01，c00是待定系數。

該曲面模型的誤差平方和為：

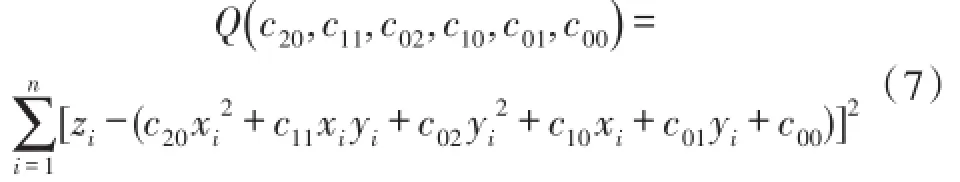
式中，（xi，yi，zi），i=1，2，…，n是采樣數據。

求解二元二次多項式待定系數的原則是使曲面模型的誤差平方和達到最小［10］。由微積分知識可知，該問題即求解六元函數Q（c20，c11，c02，c10，c01，c00）的極值，聯立方程：

可解得待定系數［11］。

3　流量檢定實驗及數據分析

3.1實驗與測試平臺

實驗平臺為三宇熱能表檢定裝置，可用于檢定超聲波熱量表流量計量的精確度。檢測臺的流量計量精確度為0.000 1 m3/h，溫度測量精確度為0.1℃。實驗中選用5塊DN20的超聲波式熱量表，量程為0～5.0 m3/h。

3.2實驗方案

3.2.1數據采集

本實驗通過建立溫度和流量之間的非線性映射模型實現流量計量的溫度補償，因此需要采集檢測臺和未經溫度補償的超聲波式熱量表在不同溫度、流量下測得的瞬時流量值，為曲面模型建模提供樣本數據，同時也驗證溫度對超聲波式熱量表流量計量精確度的影響。實驗中采樣的溫度點有（單位：℃）：30、35、40、45、50、55、60、65、70、75，流量點（單位：m3/h）有：0.05、0.1、0.25、0.3、0.4、0.5、0.6、0.75、0.8、0.9、1.0、1.1、1.2、1.3、1.4、1.6、1.8、2.0、2.2、2.4、2.6、2.8、3.0、3.5、4.0、4.5。

在采集數據時，要等到瞬時流量穩定之后再開始記錄。對每塊超聲波熱量表在不同溫度、流量下測得的瞬時流量值至少采集4次，然后取平均值作為該溫度、流量下的測量值。檢測臺測得的瞬時流量值作為目標值。

從圖4可以看出，流量計量的精確度受溫度的影響。在同一流量點下，流量計量誤差隨著溫度的升高而減小。流量計量的精確度還與瞬時流量有關。相同溫度下，瞬時流量越小，誤差越大。當瞬時流量小于0.5 m3/h時，誤差隨著瞬時流量的增大迅速減小。當瞬時流量大于0.5 m3/h時，誤差變化平緩，趨于穩定。因此采取按瞬時流量分段曲面擬合的方法改善擬合效果。

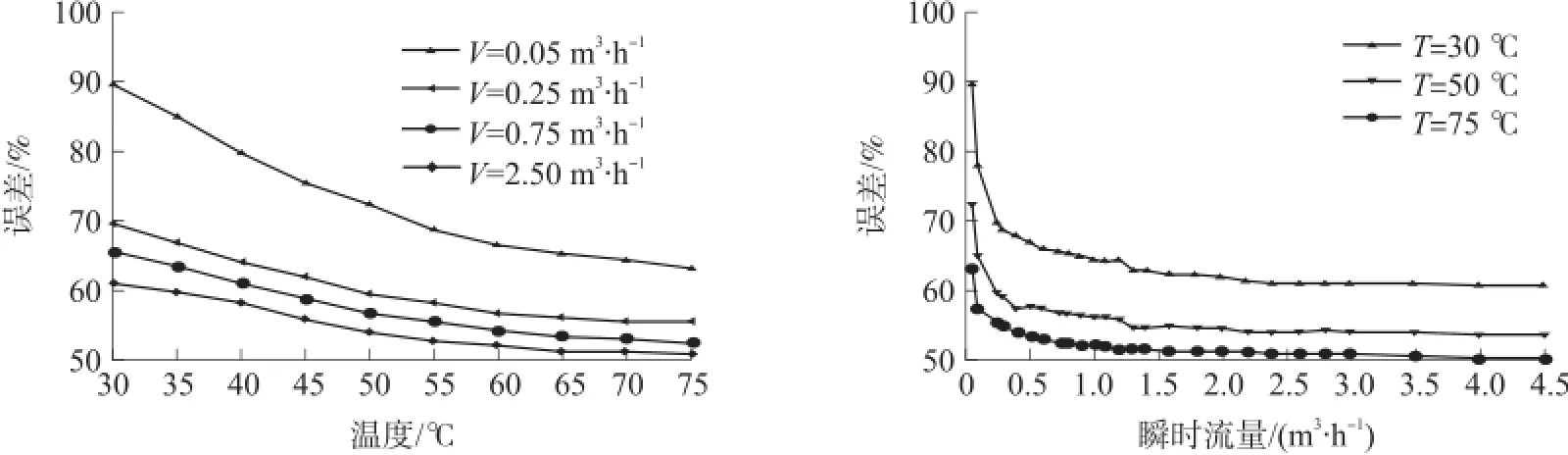
圖4　流量計量誤差隨溫度、流量變化曲線圖

3.2.2分段建模

根據最小二乘曲面擬合原理，分別求解各擬合曲面模型。通過比較各擬合曲面模型的評價參數，選擇擬合效果最好的二元二次多項式曲面模型。其表達式為：

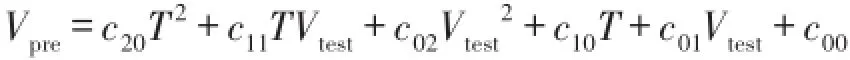
式中，Vpre為預測瞬時流量值，Vtest為超聲波式熱量表實測的瞬時流量均值，T為流體溫度。

以0.1 m3/h、0.6 m3/h、1.2 m3/h為界分段擬合。解得不同瞬時流量區間的擬合曲面模型的待定系數和評價參數如表1和表2所示。

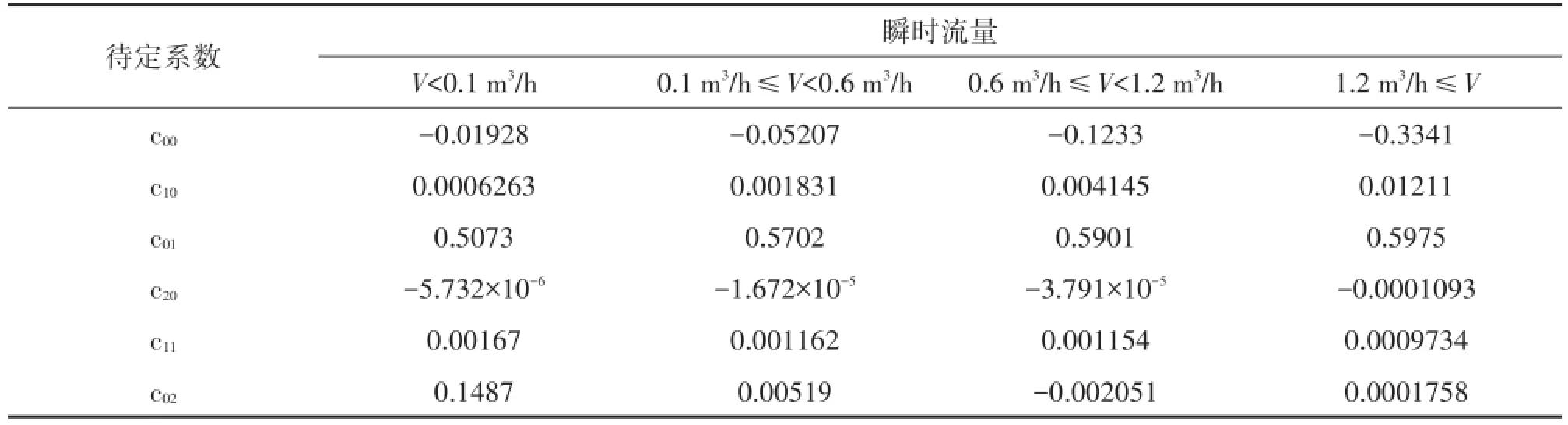
表1　擬合曲面模型待定系數

表2　擬合曲面模型評價指標

（3）仿真驗證

建模完成之后，把之前采集的樣本數據代入對應的擬合曲面模型。在不同溫度、流量下預測值與目標值的誤差如圖5所示。

圖5　不同溫度、流量下預測值和目標值的誤差曲線

從圖5可以看出，基于最小二乘曲面擬合的溫度補償算法補償效果顯著。不同溫度、流量下預測值和目標值的誤差在-2%到1%之間波動，達到超聲波式熱量表二級表的流量計量誤差要求。當瞬時流量小于1.2 m3/h時，誤差波動較大。當瞬時流量大于1.2 m3/h時，誤差趨于穩定。

圖6　最小二乘曲面擬合算法溫度補償后流量計量誤曲線

4　實驗驗證及數據分析

4.1算法移植

為了實現實時溫度補償，將擬合曲面模型移植到超聲波式熱量表程序中。當超聲波式熱量表測得未經溫度補償的瞬時流量和流體溫度時，先根據實測瞬時流量所在區間選擇對應的曲面模型，然后把實測瞬時流量和流體溫度代入曲面方程計算得到預測流量，實現流量計量實時溫度補償［12］。

4.2實驗驗證及數據分析

利用檢測臺對分別使用最小二乘曲面擬合算法和經過二次修正后的查表法進行溫度補償的超聲波式熱量表進行流量檢定實驗。根據JJG225檢定規程和行業標準，流量檢定點（單位：m3/h）選擇：0.05、0.25、0.75、2.5。使用兩種不同溫度補償方法的超聲波式熱量表在不同溫度的流量計量誤差如圖5、圖6所示。

圖7　查表法溫度補償后流量計量誤差曲線

表4　查表法與最小二乘曲面擬合算法流量計量誤差比較

由圖6、圖7及表4可知：在小流量點時，使用查表法溫度補償的超聲波式熱量表流量計量誤差在±3%以內，誤差絕對值均值為2.15%，誤差方差為4.80，流量測量值波動大，補償效果不穩定。使用最小二乘曲面擬合算法溫度補償的超聲波式熱量表流量計量誤差在±2.0%以內，誤差絕對值均值為0.72%，誤差方差為0.16。相比查表法，最小二乘曲面擬合算法整體誤差更小，補償效果更穩定。在大流量點時，兩種方法效果相當。從表3可以看出使用最小二乘曲面擬合算法溫度補償后的超聲波式熱量表在大流量點可達到1級表水平，在小流量點可達到2級表水平。

4.3多溫度點誤差二次修正算法

由于硬件原因，不同超聲波式熱量表在計量特性方面存在差異。在數據采集和實驗驗證過程中，我們發現個別熱量表在小流量點的流量計量誤差與其他熱量表相比整體偏大。在使用最小二乘曲面擬合算法溫度補償后，該表在小流量點的流量計量誤差仍然偏大，甚至超出±3%。因此，有必要對其進行二次修正。

當溫度變化較大時，熱量表在小流量點的流量計量誤差變化較大，比如在低溫下流量計量誤差為正，在高溫下可能為負。如果只根據單個溫度點的流量計量誤差對整體進行誤差修正，可能會導致其他溫度點的流量計量誤差變大，即只能實現局部最優。因此考慮采取多溫度點誤差二次修正的方法實現流量計量的全局優化。

當溫度變化較小時，熱量表的流量計量誤差變化幾乎可以忽略不計。所以在一定溫度范圍內可以按照相同流量計量誤差進行二次修正。本實驗中，選取4個溫度點，在相鄰兩個溫度點之間每3℃按照同一個流量計量誤差進行修正。假設通過檢測臺分別測得熱量表在33℃和48℃的流量計量誤差α和β。在35℃和49℃之間以3℃為步長劃分為5小段。本實驗中各溫度區間的誤差權值取值如下：（1，0），（0.8，0.2），（0.6，0.4），（0.4，0.6），（0.2，0.8），（0，1）。小于35℃按誤差α修正；在35℃～38℃之間，按0.8α+0.2β修正；在35℃～38℃之間，按0.6α+ 0.4β修正；依此類推，在46℃～49℃之間，按誤差β修正。誤差權值根據當前溫度越接近哪個溫度點，對應的誤差權值越大的原則來確定。此外，還選擇63℃和77℃作為修正點，確保實現全局修正。在其他相鄰溫度點之間也是根據相鄰兩個溫度點的流量計量誤差和誤差權值合成修正值。

多溫度點誤差二次修正前后對比如圖8所示。

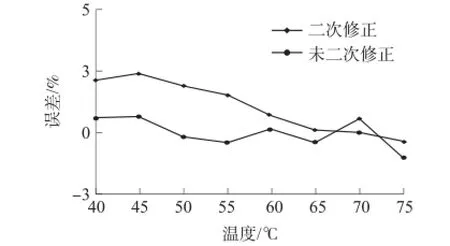
圖8　0.05 m3/h下多溫度點誤差二次修正前后流量計量誤差對比

查表法是對時差法流量計算公式中的各項參數補償，包括對超聲波波速的補償，對流速修正系數的補償等。而最小二乘曲面擬合算法和BP神經網絡算法都是通過建模直接對不同溫度（30℃～80℃）、瞬時流量（0～5.0 m3/h）下的流量計量結果補償。顯然，后者采樣數據更大。查表法速度更快，但是精度偏低。BP神經網絡算法建模復雜，而且由于模型的特殊性，很難對誤差進行二次修正。最小二乘曲面擬合算法簡單易行，而且可以對誤差進行二次修正，符合生產實際和需求。

5　結論

通過理論分析和實驗驗證得出，溫度對超聲波式熱量表中流量計量的精確度有著不可忽視的影響。在高精確度的測量中，必須要進行溫度補償。提出了基于最小二乘曲面擬合的溫度補償算法，并通過實驗證明最小二乘曲面擬合算法可以實現超聲波式熱量表中流量計量的溫度補償。在小流量點補償效果比二次修正后的查表法更穩定、更好。在實現溫度補償的基礎上，針對超聲波式熱量表自身計量特性的差異提出了多溫度點誤差二次修正算法，提高了算法的通用性，適合在工業生產中推廣應用。

［1］Yin-Jing G，Zhi-Wen L，Yuan Z.Design of Transit-Time Differ?ence Ultrasonic Heat Meter Based on TDC-GP21［J］.Journal of Measurement Science and Instrnmentation，2012：14-17.

［2］Choi H M，Yoon B R，Kim C G，et al.Evaluation of Flowmeters for Heat Metering［J］.Flow Measurement and Instrumentation，2011，22（5）：475-481.

［3］崔曉志，王翥.超聲波熱量表流量計量中溫度補償算法研究［J］.傳感技術學報，2015，28（8）：1169-1175.

［4］黃僑蔚.帶流動調整器U型聲道超聲波流量計流場特性仿真及優化［D］.華南理工大學，2013.

［5］趙文明，邵仙鶴，王玲，等.超聲波流量測量影響因素的研究［J］.自動化儀表，2012，33（9）：80-82.

［6］王翥，崔曉志，侯春雷.超聲波傳感器接收信號強度非對稱性分析及對策［J］.傳感技術學報，2015，28（1）：81-85.

［7］李坡，李毅堂，王錫鋼，等.溫度補償對超聲波熱量表流量測量影響的研究［J］.商品與質量：消費研究，2015.

［8］汪大鵬，吳憲平，夏卿坤.雷諾數的溫度特性［J］.傳動技術，2006，20（3）：11-14.

［9］.Solving Problems in Scientific Computing Using Maple and Mat?lab?［M］.Springer Science&Business Media，2011.

［10］Total Least Squares and Errors-in-Variables Modeling：Analysis，Algorithms and Applications［M］.Springer Science&Business Media，2013.

［11］Kumar J，Shunmugam M S.Fitting of Robust Reference Surface Based on least Absolute Deviations［J］.Precision Engineering，2007，31（2）：102-113.

［12］張艷鋒，嚴家明.基于最小二乘法的壓力傳感器溫度補償算法［J］.計算機測量與控制，2008，15（12）：1870-1871.

邵仙鶴（1971-）女，通信作者，哈工大（威海）副教授，主要研究方向傳感器及檢測技術、模式識別等，shaoxianhe@ali?yun.com；

魯志成（1991-），男，山東臨沂人，哈工大（威海）信電學院研究生。研究方向為傳感器及檢測技術，18766312596@ 139.com。

EEACC：7320W；782010.3969/j.issn.1004-1699.2016.06.018

基于最小二乘曲面擬合的流量計量溫度補償算法*

邵仙鶴*，魯志成，王翥
（哈爾濱工業大學（威海）信息與電氣工程學院，山東威海264209）

針對時差法超聲波式熱量表流量計量結果受流體溫度影響而存在的非線性誤差問題，提出了基于最小二乘曲面擬合的溫度補償算法，通過建立溫度和流量之間的非線性映射模型實現溫度補償。在實現溫度補償后，針對超聲波式熱量表自身計量特性的差異，進一步提出多溫度點誤差二次修正算法，根據相鄰溫度點的流量計量誤差和可變權值計算當前的流量計量誤差，對誤差進行二次修正，實現流量計量的全局優化。實驗表明，流量計量誤差在±2.0%以內，具有較高的工程應用價值。

超聲波式熱量表；流量計量；溫度補償；最小二乘曲面擬合；誤差修正

TB937；TB941

A

1004-1699（2016）06-0897-06

2015-10-07修改日期：2016-02-11

項目來源：山東省科技發展計劃項目（2012GGX10110）；山東省科技發展計劃項目（2013GGX10129）；山東省自然科學基金項目（ZR2014FM026）