含裂紋故障的轉子-軸承系統的非線性特性分析*
張亞輝 趙 軍
(91267部隊 福州 350600)
ZHANG Yahui ZHAO Jun
(No.91267 Troops of PLA, Fuzhou 350600)
?
含裂紋故障的轉子-軸承系統的非線性特性分析*
張亞輝趙軍
(91267部隊福州350600)
針對含有初始彎曲轉子系統在運行過程中出現的裂紋故障問題,建立了含有裂紋故障的轉子分析模型,推導了其運動微分方程。采用數值方法分析研究裂紋深度、初始彎曲對系統振動的影響。結果表明:隨著無量綱裂紋深度的增加,系統發生倒分岔現象提前;當考慮初始彎曲時,系統響應在臨界轉速附近的混沌區域比不考慮時增大,且隨裂紋深度增大變化緩慢。并進一步研究分析了初始彎曲量對系統振動特性的影響。論文的研究工作能夠更加真實地模擬出實際轉子系統的響應特征,更好地為轉子系統的安全穩定運動和故障的診斷提供理論參考。
裂紋; 轉子系統; 非線性振動
ZHANG YahuiZHAO Jun
(No.91267 Troops of PLA, Fuzhou350600)
Class NumberTB561;U661.42
1 引言
轉子是航空和船用汽輪機組的關鍵部件,其工作環境非常惡劣,長期處于高溫介質中高速旋轉,逐漸形成疲勞裂紋源進而擴展,裂紋會導致轉軸剛度降低,從而引起轉子橫向振動幅值變大,形成運行故障進而影響機組正常工作,嚴重影響飛機和船舶在航率和安全性。引起轉子異常振動或振動過大的原因有很多,轉軸裂紋是主要原因之一[1]。
工程實際中,轉子的彈性軸有時會存在一定的初始彎曲,即彈性軸在不受力的情形下其軸線并不是一條理想的直線。造成轉子初始彎曲的原因各不相同,有制造安裝誤差的問題,也有運行中熱效應等問題。轉子的彈性軸出現彎曲后,必然引起相應的質量偏心,造成轉子的動擾度增加,機組的振動加劇,甚至能引發轉子與靜子之間的碰摩[2]。
甕雷,楊自春等[3~4]分析研究了氣流激振力作用下轉子系統的非線性振動特性。張韜、孟光[5]分析了具有初始彎曲和剛度不對稱轉子系統的碰摩響應,得到了參數對系統分叉和混沌響應的影響。林富生,孟光[6]以飛行器內等速運動的同時存在初始彎曲和橫向裂紋的轉子軸為研究對象,分析研究了飛行器機動飛行對轉子系統振動響應的影響。
以上文獻都是基于簡單的模型分析初始彎曲對裂紋轉子系統的動力學響應,而工程實際中轉子系統非常復雜,為了更進一步研究初始彎曲對裂紋轉子振動特性的影響,本文綜合考慮了非線性油膜力以及裂紋交叉剛度,建立了含初始彎曲的轉子-軸承系統。通過數值仿真,分析研究了初始彎曲和裂紋深度對系統的振動響應。
2 系統動力學方程
本文以含有裂紋故障的對稱剛性油膜支承的轉子-軸承系統作為研究對象,忽略扭轉振動和陀螺力矩,只考慮轉子的橫向振動,如圖1所示,研究在汽輪機非線性間隙氣流激振力作用下的非線性動態響應。其中O1、O2分別為軸承內瓦和轉子幾何中心,O3為轉子質心;轉子兩端由半徑為R、長為L的滑動軸承支承,m1、c1和m2、c2分別為轉子在軸承處和圓盤處的等效集中質量和結構阻尼,e為圓盤的質量偏心,Fx、Fy為非線性油膜力[7]。
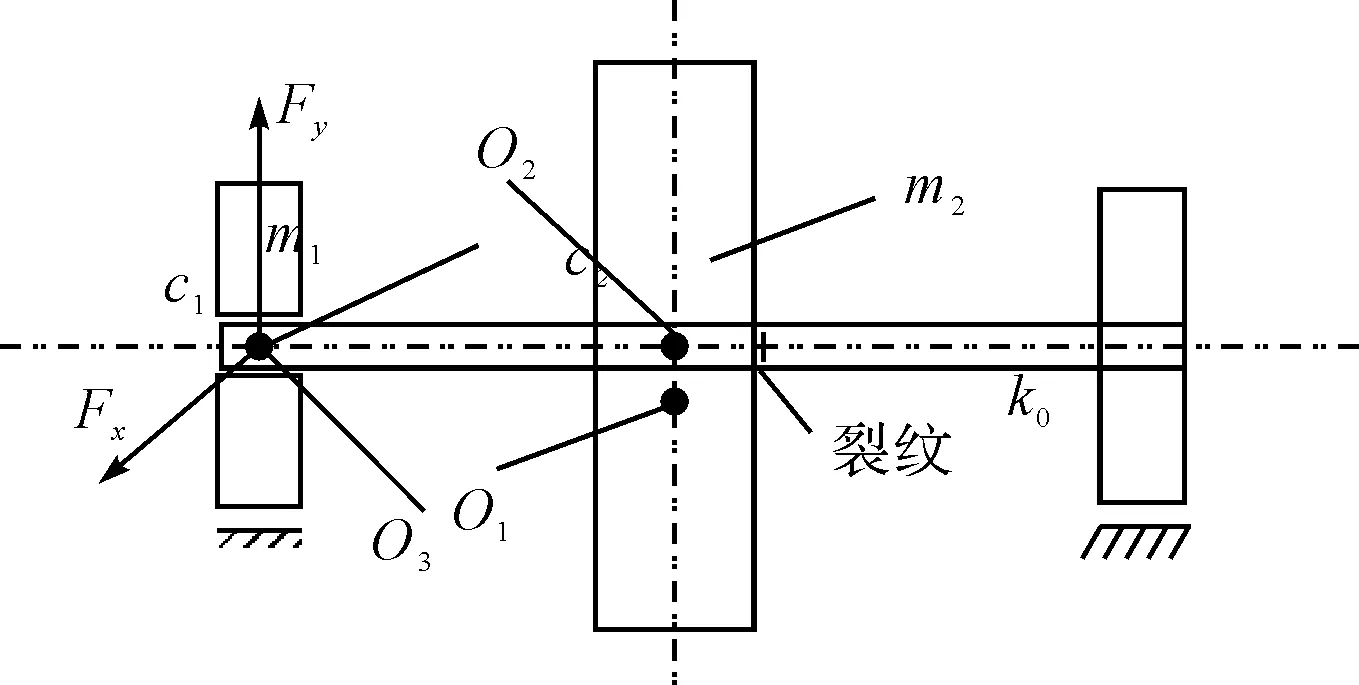
圖1 油膜支承裂紋轉子系統示意圖
2.1裂紋剛度模型
轉子軸在無裂紋時的剛度為k0,kxx為x方向的剛度;kxy、kyx為x,y方向交叉的剛度;裂紋在ξ方向和η方向的剛度變化量為kξ和kη;ω為轉速;β為不平衡量與裂紋法向的夾角。轉子系統的剛度矩陣無量綱形式可表示為[8]
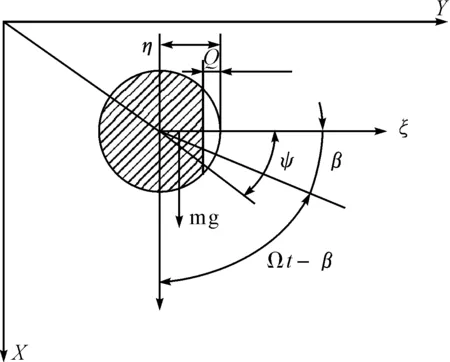
圖2 轉子裂紋軸橫斷面示意圖

(1)
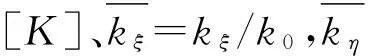
(2)
開閉函數當a/R<0.5時采用GASCH的鉸鏈彈簧模型,a/R≥0.5時采用MAYES提出的裂紋模型[9],開閉函數表達式如下:

(3)
2.2轉子運動微分方程
只考慮系統的橫向振動,忽略扭轉振動和陀螺力矩,則在非線性油膜力作用下考慮初始彎曲的含
裂紋轉子系統運動微分方程的無量綱運動微分方程如下:
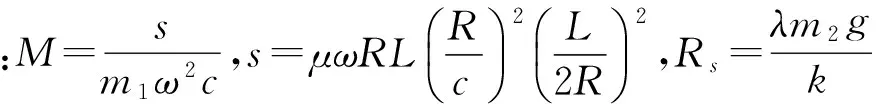
3 仿真結果與分析
鑒于本文運動微分方程具有強非線性特征,采用四階龍格庫塔方法研究分析參數變化時系統的各種動力學現象,獲取不同參數變化下的振動響應,進而給出在非線性油膜力作用下含有初始彎曲的轉子在裂紋故障時的振動分岔圖、軸心軌跡和Poincare截面圖。
本文轉子軸承系統的主要參數為:m1=4.0kg,m2=32.1kg,R=25mm,L=12mm,μ=0.018pa·s,c1=1050N·s/m、c2=2100N·s/m、k=2.5×106N/m,b=0.11mm,氣流激振力的參數選取如下:ρ0=11.8kg/m3,RT=0.5m,RB=0.37m,β1=35°,β2=40°,ζ=0.83,δ=1.2×10-3m,V=200m/s。系統一階臨界轉速為ω0=882.5rad/s。
3.1裂紋深度對系統動力學特性的影響
裂紋深度對轉子系統的非線性動力學響應產生不同的影響。如圖3和圖4所示,分別給出了初始彎曲量為λ=0.3時,在非線性油膜力作用下不考慮和考慮初始彎曲時不同裂紋深度下裂紋轉子軸承系統的振動響應隨轉速ω變化的分岔圖。圖3為不考慮初始彎曲的裂紋轉子系統的分岔圖,與文獻[10]中的分岔圖類似,但文獻采用的是余弦波模型,雖然考慮了裂紋之間的開閉的過度過程,但沒能較好地反映裂紋的常開與常閉階段,這與實際情況也是不相吻合的。
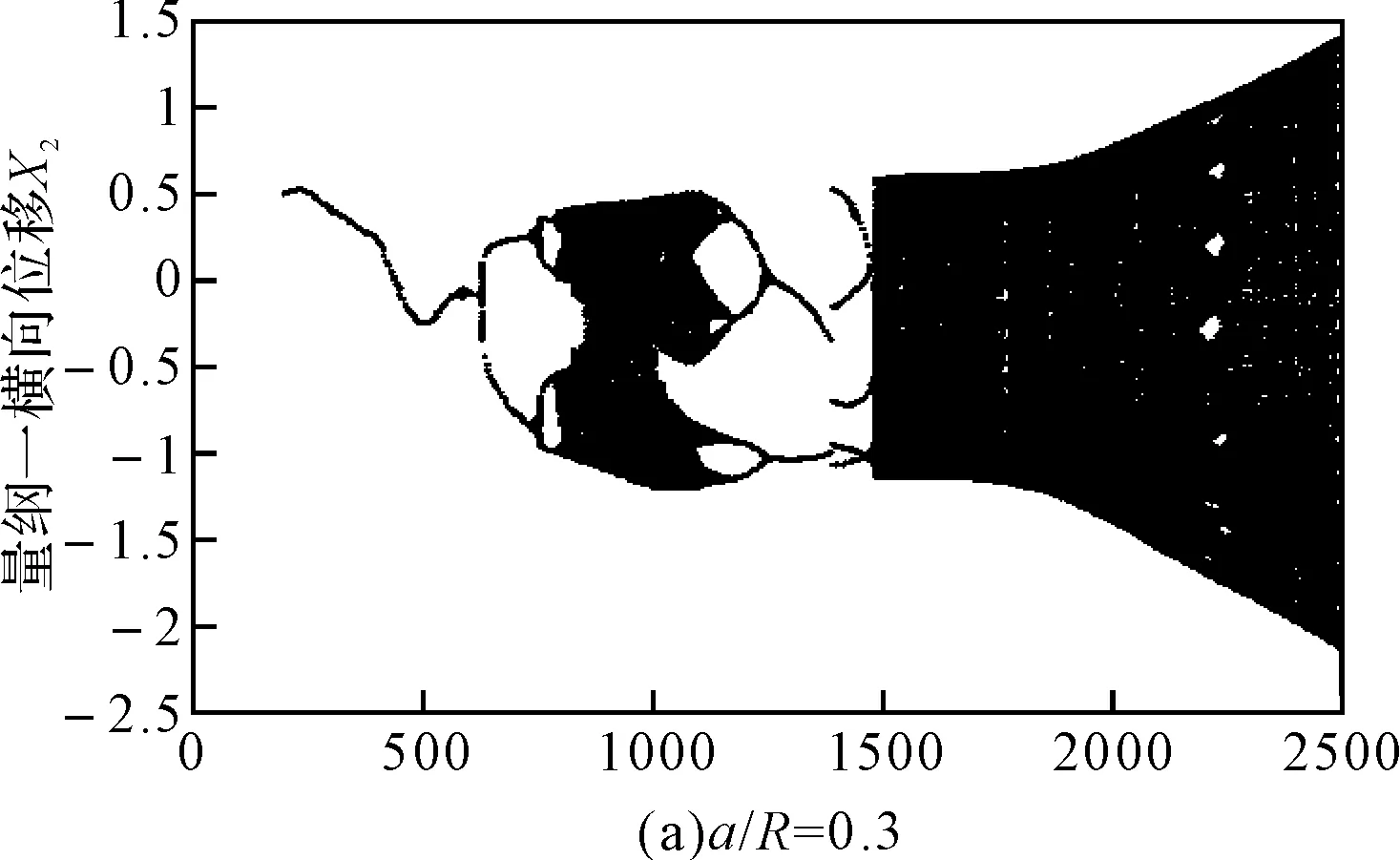
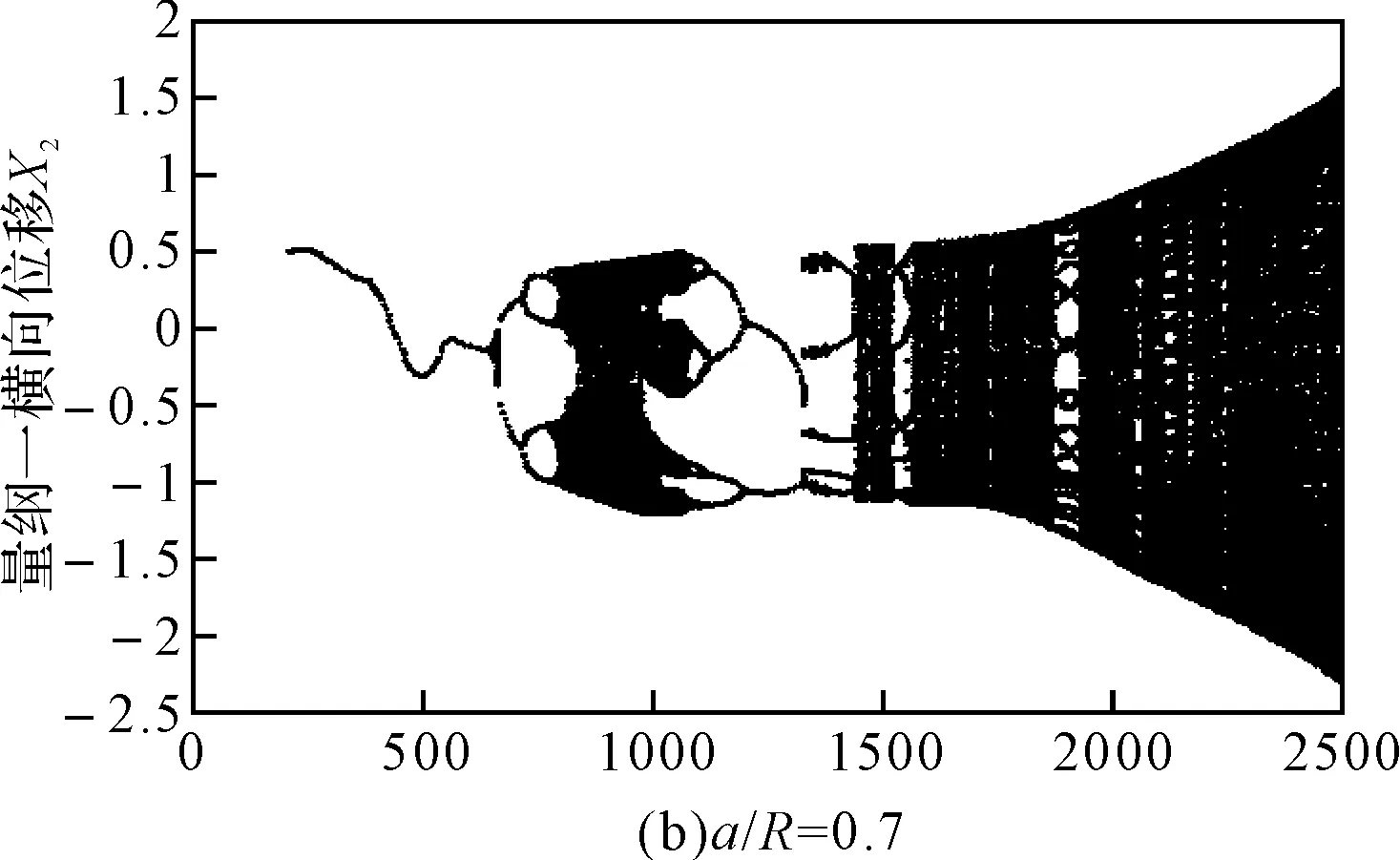

圖3 無初始彎曲時不同裂紋深度系統隨轉速變化的分岔圖
本文采用的模型可以綜合考慮裂紋深度對裂紋軸剛度的影響,能夠更加準確地說明含裂紋轉子系統隨裂紋深度變化的動力學響應。從圖3可以看出,在轉速比較低時,無量綱裂紋深度對轉子系統的動力學響應影響較小,而對臨界轉速和超臨界轉速區域的動力學特性影響比較大。對比圖3(a)、3(b)和3(c)可以看出,隨著無量綱裂紋深度的增加,系統發生倒分岔現象提前,臨界轉速區域的混沌區域逐漸減小;由圖3(b)和3(c)可以看出系統在超臨界轉速區域出現周期8和較長的周期3運動,且系統在臨界轉速區域的分岔圖演變為兩條自相似的軌跡。

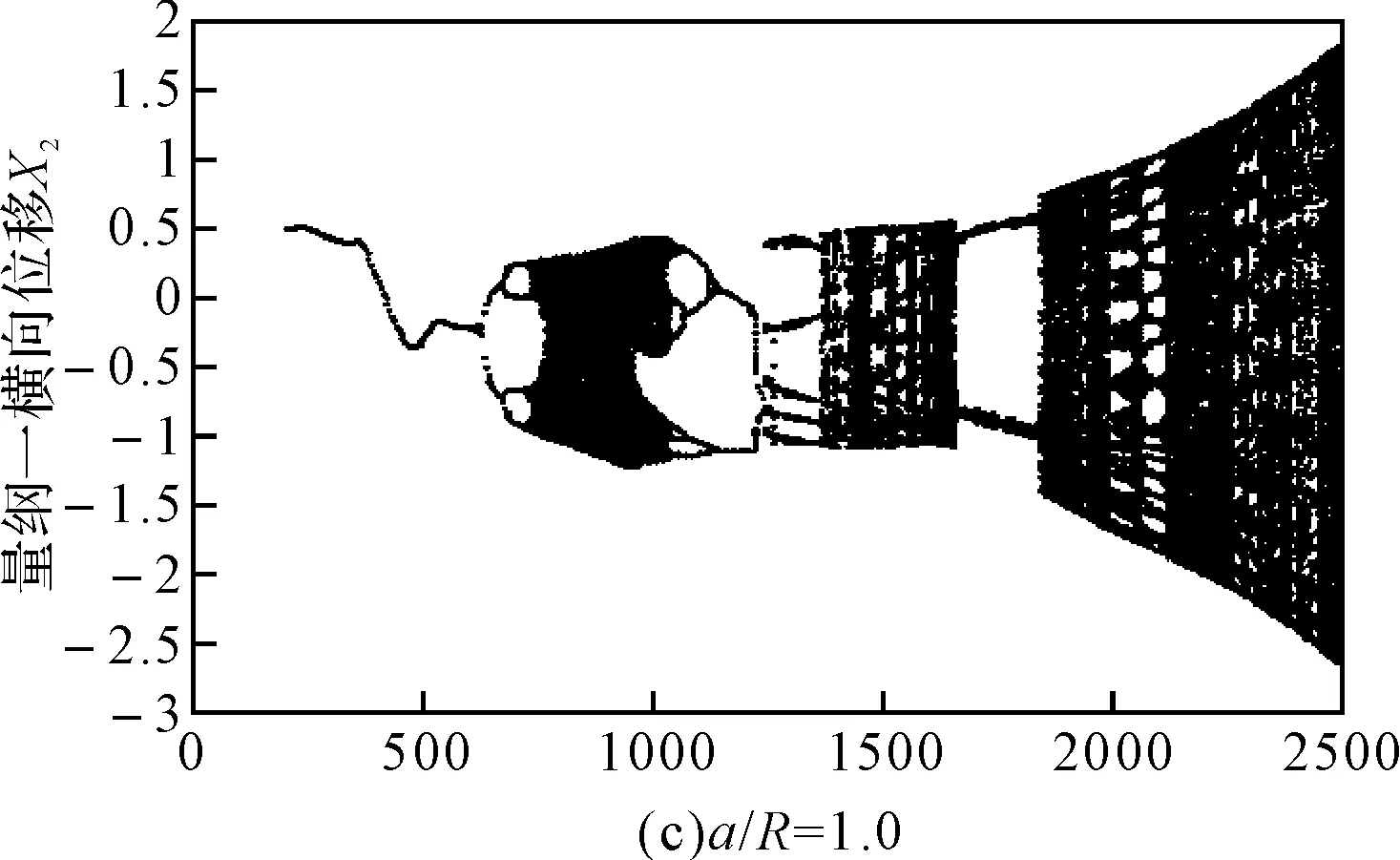
圖4 含初始彎曲時不同裂紋深度系統隨轉速變化的分岔圖
由圖4可以看出,隨著無量綱裂紋深度的增加,系統發生倒分岔現象提前,臨界轉速區域的混沌區域也逐漸減小,但相對無初始彎曲時變化不大;在超臨界轉速區域出現周期8和較長的周期2運動。對比圖3和圖4可以看出,轉子系統隨著無量綱裂紋深度的增加,在考慮初始彎曲時,轉子系統響應在臨界轉速附近的混沌區域比不考慮初始彎曲時增大,隨裂紋深度變化較無初始彎曲時變化緩慢,這主要是由于初始彎曲的存在使得系統的響應復雜化。因此,進一步研究初始彎曲對系統動力學響應的影響,是很有必要且十分有意義的。
3.2初始彎曲量對系統動力學特性的影響
為了進一步研究初始彎曲量對系統動力學特性的影響,以初始彎曲量λ作為控制參數,研究其變化對轉子系統動力學行為的影響。圖5給出了無量綱裂紋深度a/R=1.0、轉速ω=1050rad/s時轉子系統隨初始彎曲量變化的響應分岔圖。由圖可以看出,隨著初始彎曲量的增大,在油膜力和轉子質量偏心作用下裂紋故障轉子系統呈現出不同的非線性特征。

圖5 無量綱裂紋深度a/R=1.0時振動響應隨初始彎曲量變化圖
在初始彎曲量較小時,系統呈現出周期4運動,如圖6(a)所示,系統的軸心軌跡為4條交叉曲線,在Poincare截面上表現為4個離散的點。隨著初始彎曲量的增大,轉子的振動響應演變為周期8運動,如圖6(b)所示,系統的軸心軌跡為8條交叉曲線,在Poincare截面上表現為8個離散的點。隨著初始彎曲量的進一步增大,轉子系統經過周期性分岔進入混沌運動,當λ=0.512時,系統出現短暫的周期12運動,如圖6(c)所示,Poincare截面上為12個離散的單點,軸心軌跡為有限條曲線。之后又進入復雜的混沌運動。
圖7給出了無量綱裂紋深度a/R=0.7、轉速ω=1050rad/s時轉子系統隨初始彎曲量變化的響應分岔圖,由圖可以看出系統的響應在初始彎曲量λ=0.629附近出現短暫的周期12運動外,都處于混沌運動狀態。圖8為不同初始彎曲量下轉子系統的軸心軌跡圖和Poincare截面圖。對比圖5、6和圖7、8可以看出:在無量綱裂紋深度較小時,系統的動力學響應主要受初始彎曲的影響,系統響應除了出現短暫的周期12運動外,基本上處于混沌運動狀態;隨著無量綱裂紋深度的增加,無量綱裂紋深度導致系統的動力學特性逐漸變得明顯,在不同的初始彎曲量下系統的響應交替出現周期運動和混沌運動。

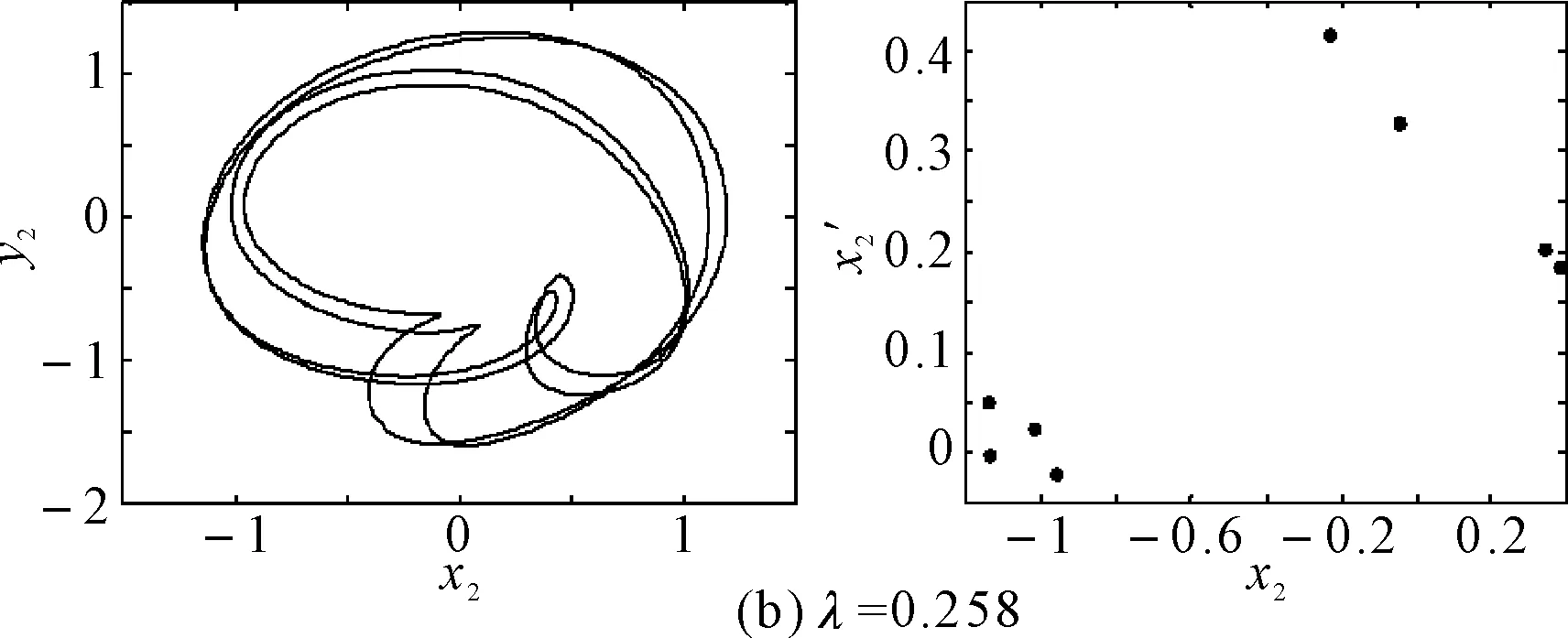

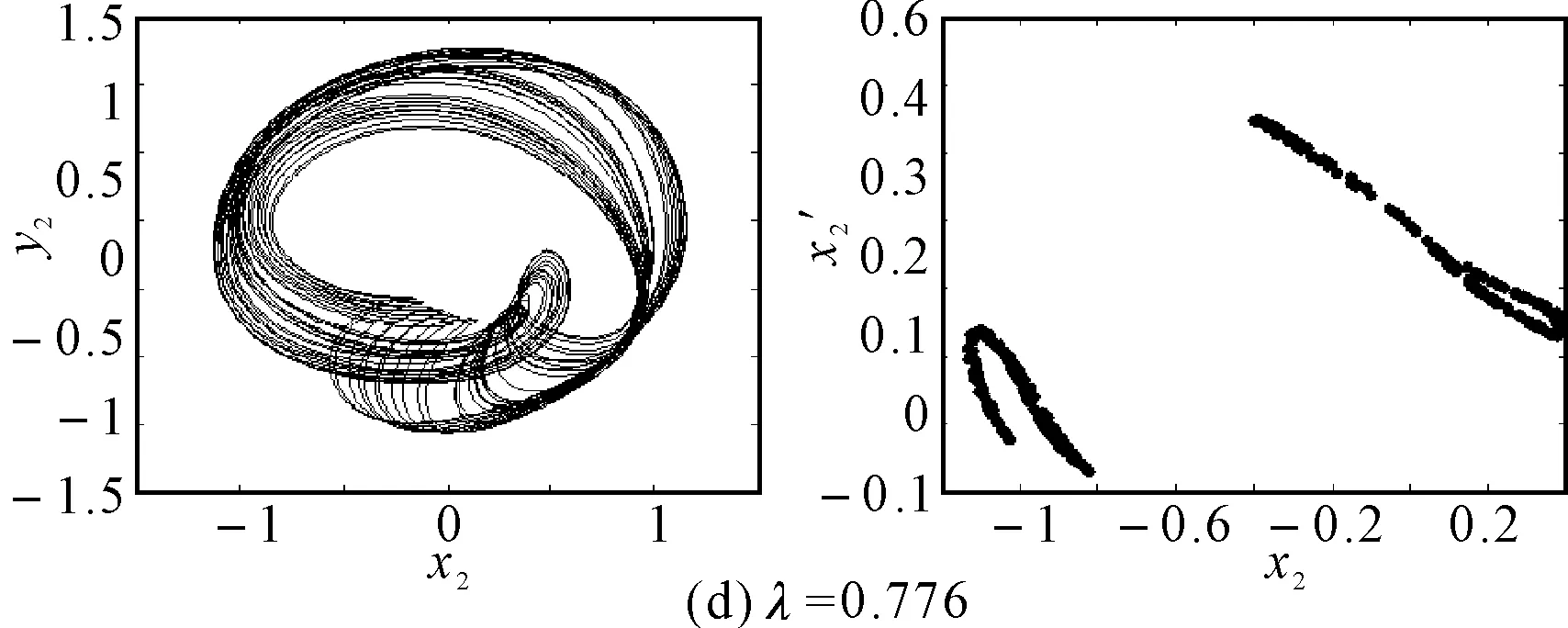
圖6 裂紋深度a/R=1.0不同初始彎曲時轉子軸心軌跡和Poincare截面圖
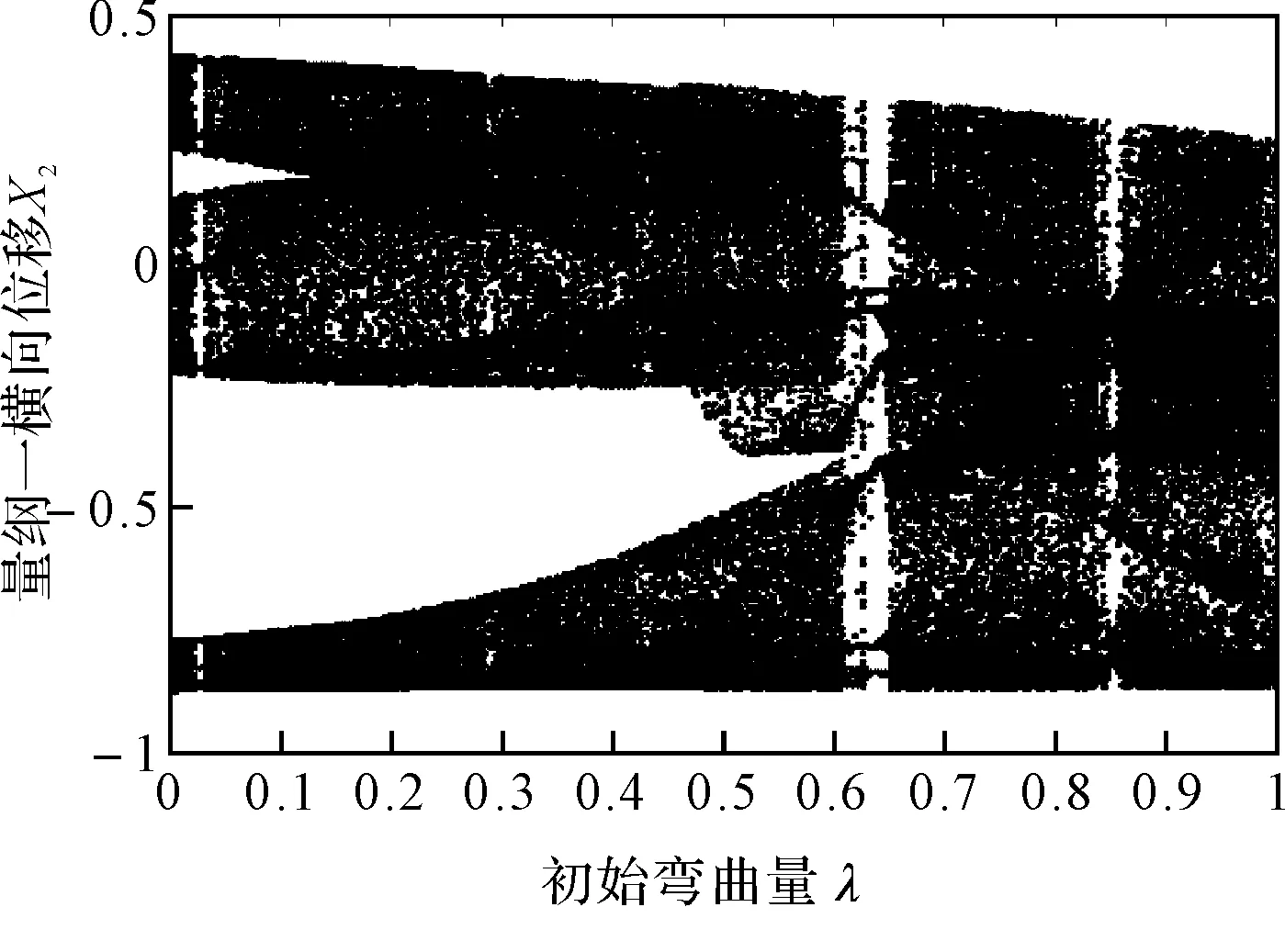
圖7 無量綱裂紋深度a/R=0.7時振動響應隨初始彎曲量變化圖
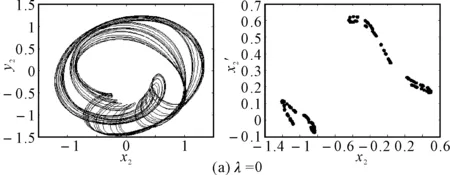
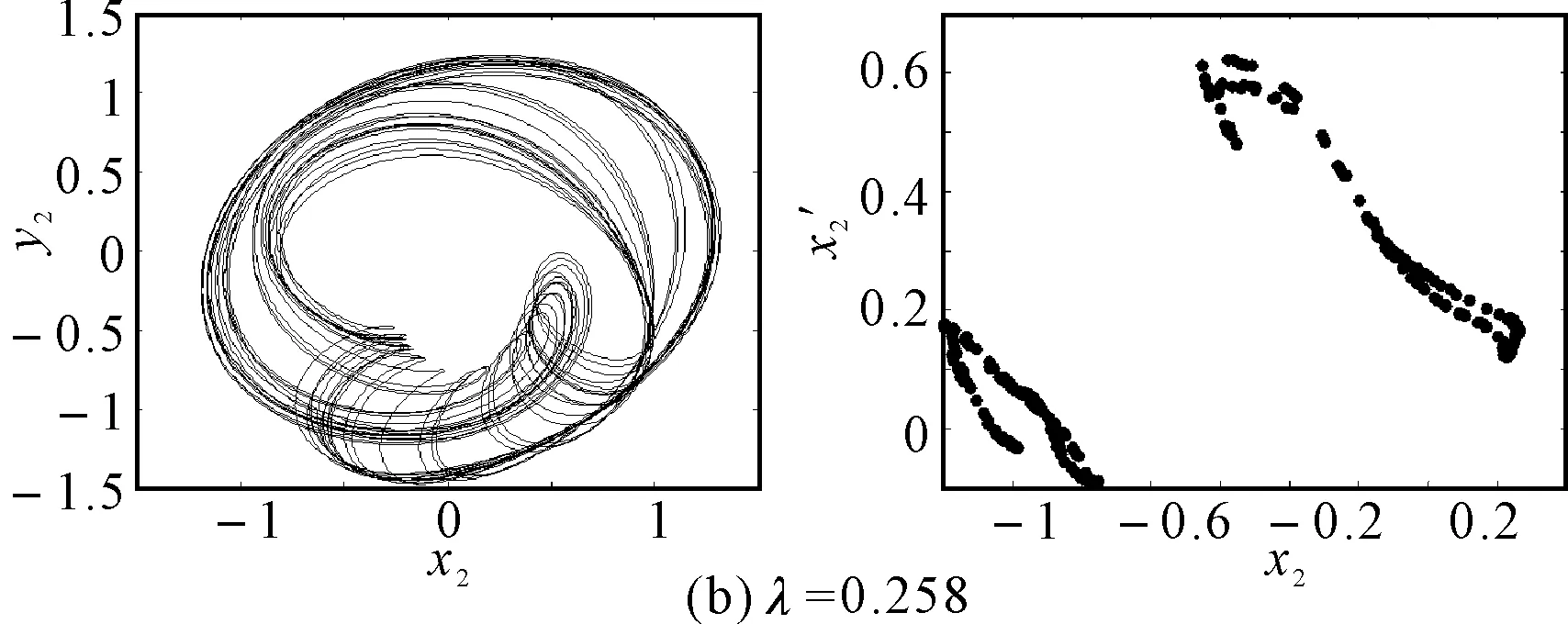

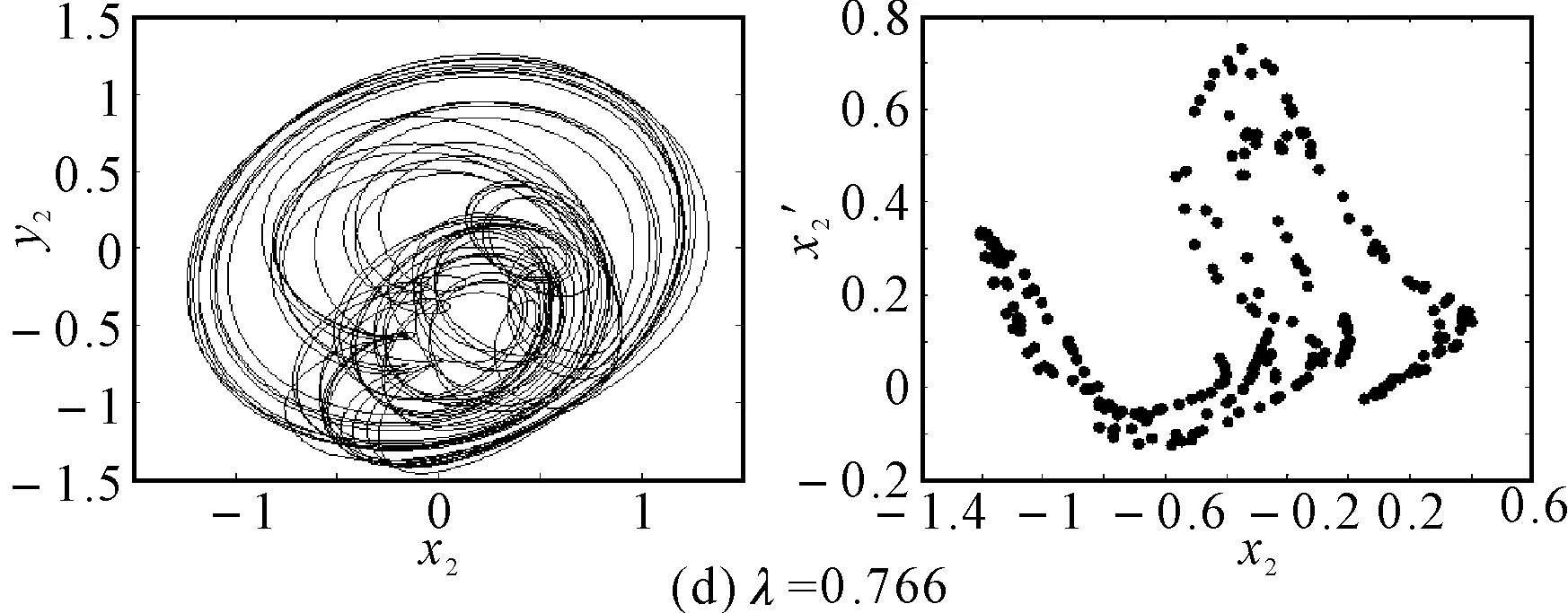
圖8 裂紋深度a/R=1.0不同初始彎曲時轉子軸心軌跡和Poincare截面圖
4 結語
本文建立了在非線性油膜力和轉子質量偏心作用下,考慮初始彎曲的含有裂紋故障的轉子系統動力學分析模型,推到了系統的運動微分方程,通過數值仿真方法分析了在不同裂紋深度和初始彎曲量對系統非線性動力學特性的影響,得出如下結論:
1) 隨著無量綱裂紋深度的增加,在轉速較低時,無量綱裂紋深度對系統的動力學響應影響較小,而對轉速在臨界轉速和超臨界轉速區域的動力學特性影響較大,且系統發生倒分岔現象提前;當考慮初始彎曲時,系統響應在臨界轉速附近的混沌區域比不考慮時增大,且隨裂紋深度增大變化緩慢,這主要是由于初始彎曲的存在使得系統的響應復雜化。
2) 進一步研究分析了初始彎曲量對系統振動特性的影響,結果表明:在無量綱裂紋深度較小時,系統的動力學響應主要受初始彎曲的影響,系統響應除了出現短暫的周期12運動外,基本上處于混沌運動狀態;隨著無量綱裂紋深度的增加,無量綱裂紋深度導致系統的動力學特性逐漸變得明顯,在不同的初始彎曲量下系統的響應交替出現周期運動和混沌運動。
本文考慮了轉子系統在實際中存在的初始彎曲,能夠更加真實地模擬出實際轉子系統的響應特征,更好地為轉子系統的安全穩定運動和故障的診斷提供理論參考。
[1] 趙常興.汽輪機組技術手冊[M].北京:中國電力出版社,2007.
[2] 黃文虎,夏送波.旋轉機械非線性動力學設計基礎理論與方法[M].北京:科學出版社,2006.
[3] 甕雷,楊自春,曹躍云.汽輪機非線性間隙氣流激振力作用下轉子系統的分岔研究[J].海軍工程大學學報,2015,27(5):52-57.
[4] 甕雷,楊自春,曹躍云.汽輪機非線性間隙氣流激振力作用下含裂紋轉子的振動特性研究[J].振動與沖擊,2016,35(5):89-95.
[5] 張韜,孟光.具有初始彎曲和剛度不對稱的轉子碰摩現象分析[J].上海交通大學學報,2002,36(6):844-848.
[6] 林富生,孟光.飛行器內含橫向裂紋的初始彎曲轉子的動力學特性研究[J].振動工程學報,2004,17(s):16-18.
[7] 楊積東,徐培民,聞邦椿.裂紋轉子分岔、混沌行為研究[J].固體力學學報,2002,23(1):115-119.
[8] LI Ruqiang,LIU Yuanfeng. Simulation of crack diagnosis of rotor based on multi-scale singular-spectrum analysis[J].Chinese Journal of Mechanical Engineering,2006,19(2):282-285.
[9] 曾復,吳昭同,嚴拱標.裂紋轉子的分岔與混沌特性分析[J].振動與沖擊,2000,19(1):40-42.
[10] 李振平,金志浩,徐培民,等.含橫向裂紋的彈性轉子-軸承系統的動力學研究[J].振動工程學報,2003,16(4):468.471.
Nonlinear Characteristics of the Rotor-Bearing System with A Crack*
The dynamic model of a rotor system with crack fault is established. Considering the initial bend deformation of the rotor, and the movement differential equation is deduced. The effects of crack depth and the initial bending on the rotor system are analyzed using numerical methods. The results indicate that the phenomenon of the bifurcation happen in advance when the dimensionless depth of crack increase. And the response with initial bending is bigger than without initial bending, and the system response changes slowly with the depth of crack increase. And the effect of initial bending on the system is also analyzed in this paper. It indicates that the research on this paper can offer better theoretical reference for the fault diagnosis and safely running of rotor system.
crack, rotor system, nonlinear vibration
2016年2月13日,
2016年3月17日
張亞輝,男,工程師,研究方向:裝備技術保障。趙軍,男,碩士,助理工程師,研究方向:裝備技術保障。
TB561;U661.42
10.3969/j.issn.1672-9730.2016.08.047

