基于邊失效的艦艇裝備保障網絡抗毀性分析*

張　肖　戴明強　邵　帥

(海軍工程大學理學院　武漢　430033)

ZHANG Xiao　DAI Mingqiang　SHAO Shuai

(College of Science, Naval University of Engineering, Wuhan　430033)

?

基于邊失效的艦艇裝備保障網絡抗毀性分析*

張肖戴明強邵帥

(海軍工程大學理學院武漢430033)

艦艇裝備保障網絡是一個包含了不同種類節點和錯綜復雜路線的復雜系統，實施保障計劃的過程中總會碰到道路故障和擁堵的情況，即邊失效。針對這一問題，分析邊失效時負載的分流機制，取網絡的繁忙程度和網絡的復雜程度兩個因素對網絡級聯效應抗毀性的影響進行研究，并構建模擬網絡模型進行仿真實驗。結果表明，網絡越繁忙，網絡復雜程度越低，網絡級聯失效抗毀性越差；而網絡復雜程度比繁忙程度對抗毀性的意義更大。

艦艇裝備保障； 邊失效； 級聯失效； 網絡抗毀性

ZHANG XiaoDAI MingqiangSHAO Shuai

(College of Science, Naval University of Engineering, Wuhan430033)

Class NumberE273

1　引言

艦艇裝備保障網絡一般位于局部沿海、相對陸上其他保障網絡較小的區域內，是主要提供海軍艦艇的裝備保障功能的物流網絡。在網絡日常運行中，在較短的時間內通過節點和邊的負載變化很小，影響保障網絡級聯失效抗毀性的更重要的因素是網絡的節點容量分布與邊的流量分配。一般艦艇需要對裝備進行保障的時間通常是在出航前或者是完成相關任務返港后。而在出航前根據任務需要，有不同的備戰備航等級，相應的時間要求也是有長有短。也有在返港之后根據需要馬上去執行下一個任務的時候，而在航行時造成的裝備損耗則需要在這兩次任務的間隙進行裝備保障。這說明艦艇裝備保障任務具有很強的應急性，對保障的速度提出了較高的要求。在道路出現損毀、擁塞(邊失效)時必然會影響保障的速度；當運輸的裝備為艦艇出航所必須時，會使整個作戰計劃延后，延誤戰機。

目前對于在裝備保障的運輸環節中出現中斷和延遲所引發的級聯失效對保障網絡抗毀性影響的研究還處于起步階段，相關研究不多。文獻[1～5]在物流網絡節點或邊失效時，采用基于無向物理網絡進行隨機比例分流的方法，對負載進行重新分流轉移。這對實際裝備保障環境下的方向性選擇缺乏考慮。另外，一些級聯失效模型假設失效節點間的邊鏈接是可移除的[5]。以上兩點均與實際保障特征有所出入，例如裝備運輸過程中在遭遇交通堵塞或其他事故的發生后，不僅存在裝備分流轉運的方向選擇問題，且發生事故的道路也并非就此完全作廢，在現場道路運輸載體上的裝備也不可能放棄不用。顯然，這些實際環境因素對于物流網絡中的級聯失效傳播有著不容忽視的影響，因此需要針對符合物流網絡中自身特征的級聯失效模型進行構建。

2　邊失效引發級聯失效的分析

研究發現，網絡中越是負載能力較大的路段或鏈接邊，其上的流量往往也越大。而隨著生產力的發展，現代交通工具也開始了爆炸式的發展。由于部分路段受到負載能力的限制，在核心路段幾乎每天都會發生擁堵。它們較其他路段或邊在突發或干擾事件下更易產生運輸中斷。本文選取物流局部網絡結構如圖1所示，假設其中任意選取的邊eij突發中斷繼而失效。考慮到現實物流運輸網絡中的邊失效后的不可移除性，本文以下所假設物流交通運輸中斷導致的邊失效只是表征運輸線路服務功能的暫時性中斷。

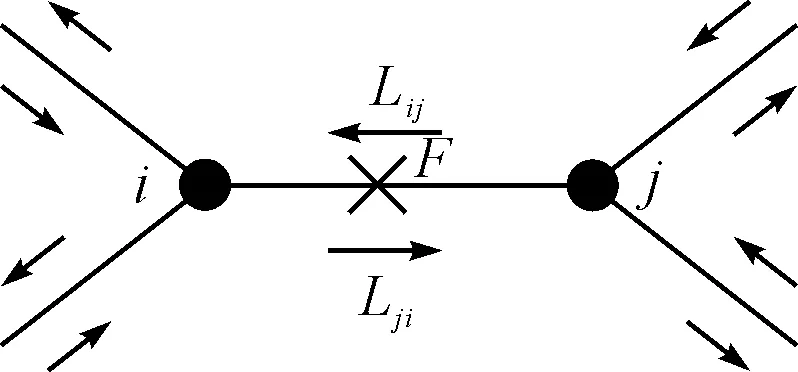
圖1　運輸中斷的局部網絡示意圖

邊eij在F處發生中斷而失效，在整個ij段上的物流負載會通過如下形式發生轉移，如圖2所示。

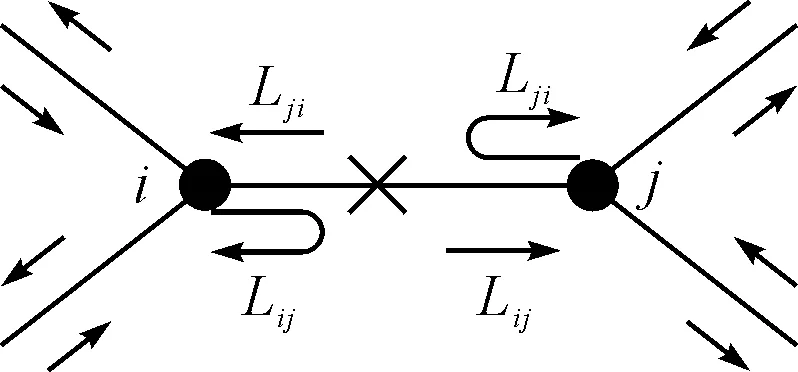
圖2　運輸中斷時負載的流向圖

1)沿著既定的方向已通過F點的負載物流則按原計劃繼續運輸至后續節點和邊。

2)未通過F點的負載物流則原路返回，通過其他的路徑來繼續完成任務。

3　裝備保障網絡級聯邊失效模型的構建

3.1網絡參數的選取

根據上一小節的分析，易知失效邊(運輸中斷所在路段)的鄰接邊(關聯路段)在網絡中的負載能力大小和重要性程度對物流運輸中斷后的失效負載分配傳遞具有主要影響。網絡的復雜性、連通性也對保障任務的物流能否到達目的地有著重要影響。

首先仍然采用介數來定義物流網絡中的運輸路段的重要性[6～7]：

(1)

其中，Be為任意邊e的介數，σgh表示為任意節點g和h之間的最短路徑的總數，σgh(e)表示任意節點g和h之間的所有最短路徑中途徑邊e的路徑數量。該定義以物流保障任務經過該路段的次數作為路段重要性的體現，很符合實際物流保障運作特征。

其次，考慮到既有的大多數研究釆用邊的兩端節點的度來對邊(運輸路段)的負載能力進行量化[8,9]，缺乏考慮邊(運輸路段)自身屬性在網絡中的重要度。另外，也不是兩端節點的每條邊都能最終鏈接到保障任務的目的地；如圖3所示，節點AB之間的邊發生中斷，返回節點B的負載LBA可以通過邊eBD到達節點D，進而到達保障任務的目的地E。而節點B與節點C之間的邊eBC則在此次任務中無法擔任分流邊。

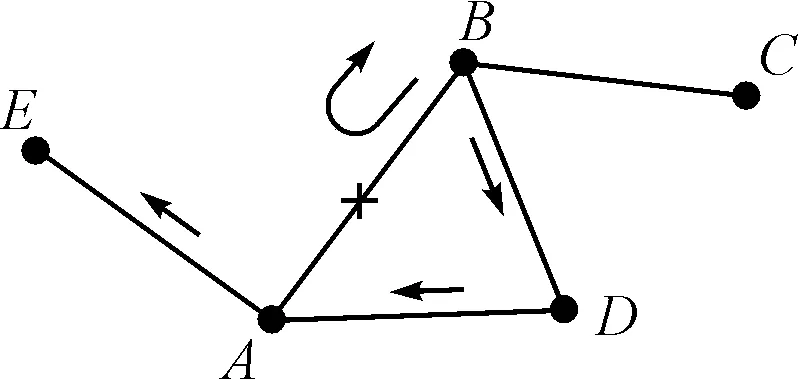
圖3　針對任務需求的分流邊

為此，本文在既有研究的基礎上加以考慮邊的介數因素，給出如下關于邊(運輸路段)負載能力的定義：假設任意邊e的負載能力Ce，具體計算如式(2)所示：

Ce=Be(kikj)θ

(2)

其中，ki和kj分別為邊(運輸路段)兩端節點i和j的度。

網絡的平均度〈k〉則能較好地反映一個網絡的復雜性和連通性。〈k〉值越大，網絡的連通性越好，執行保障任務的物流就更大可能到達原計劃目的地。〈k〉值的具體計算公式如下：

(3)

3.2分流機制

在不考慮運輸方向的情況下，失效邊e上的負載Le將根據鄰接邊在網絡中的重要度大小進行分配流量。其中，設任意的關聯鄰接邊eix獲得的失效邊的上的負載分配比例大小為pix其具體計算方式如式(4)所示：

(4)

其中，Γij為失效邊e的鄰接邊集合。

3.3模型評價指標的確立

釆用邊的損失比例R作為網絡級聯失效后的抗毀性評估指標，其計算方法具體如式(5)所示：

(5)

其中，NE為網絡的邊的數量，Nf為失效邊的數量。R的取值范圍為(0,1]。該指標值越大，說明突發事件級聯失效對網絡的破壞性越大。

4　仿真實驗

4.1實驗網絡模型

通過Matlab軟件生成節點規模為N=100的BA網絡來模擬物理網絡結構模型，其中邊的數量為393條。運用ucinet軟件得到實驗網絡拓撲結構體如圖4所示，圖中節點形狀的大小對應著節點度的大小。為不失一般性，讓節點的規模不變，將邊的數量分別隨機降至317、275、227，此時平均度〈k〉也分別降至6.3、5.5、4.5，之后與平均度〈k〉為7.8的網絡進行比對研究。

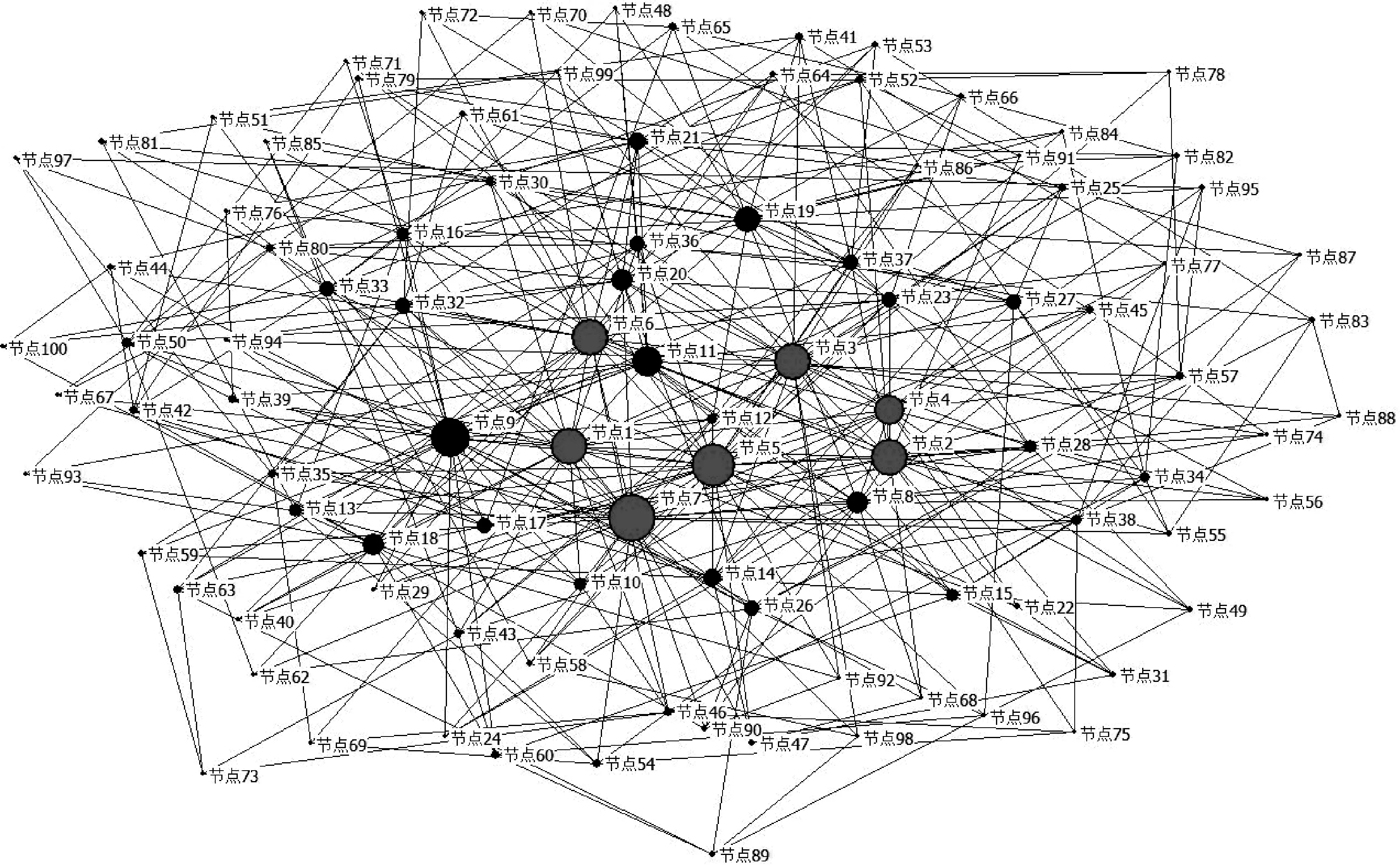
圖4　節點數為100的BA網絡

通過對該網絡的節點度分布狀況進行分析統計，如圖5所示，其中圖中橫坐標表示節點的度k，縱坐標為k的分布統計函數P(k)，表示度為k的節點所占的比例。該網絡模型具有度分布不均勻的網絡特性。

圖5　節點度分布

通常邊的負載與其容量成正比。邊的容量越大，經過邊的負載才能越大。即負載與容量呈正相關性。用數學表達式表示它們的關系為式(6)：

Lij(0)=μCijμ∈[0,1]

(6)

其中，Lij(0)為任意邊eij的初始負載。μ為控制參數，體現出負載占當前邊的總容量比，也表征了本路段的繁忙程度。而失效點F與失效邊eij兩端的空間距離的比值D?F/Dij，由于失效點發生的隨機性，在這里以隨機數ε來替代這個比值，且ε∈[0,1]。

4.2算法分析

根據上節建立的保障網絡級聯失效模型及其分析，這里給出該模型的算法：

1)網絡初始正常狀態下，任意物流邊(運輸路段)Dod的負載為Lij，負載能力為Cij，i,j=1,2,…,N。

2)初始時刻，隨機選擇任意邊(運輸路段)eij，令其突發失效。

3)根據未失效前的網絡鄰接矩陣A中非零元素aij及物流邏輯網絡方向量化矩陣Dod判斷獲得失效邊eij的關聯鄰接邊集合Γij，由失效負載分流規則即式(4)進行失效負載的分配轉移。

4)根據節點失效傳播函數判斷關聯鄰接邊eij是否崩潰失效；若失效，返回步驟2)。

5)直到再無邊(運輸路段)崩潰失效的發生，結束。

4.3實驗結果分析

先對平均度〈k〉為7.8，邊數為393的網絡進行實驗，取μ=0.8，步長M=0.02，得到控制參數μ與損失比例R的關系如圖6。

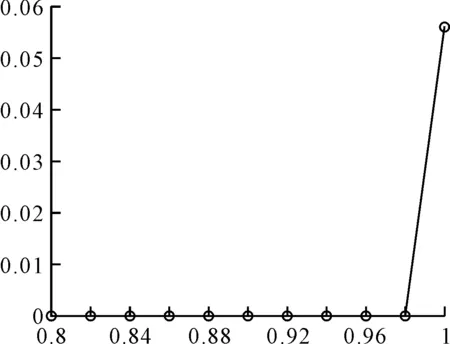
圖6　控制參數μ與損失比例R關系圖

圖6中坐標軸的橫軸表示控制參數μ，縱軸表示損失比例，由圖可知，在網絡足夠復雜、平均度〈k〉足夠大時，即使是98%的高負荷的運行，網絡中有單個邊出現失效時是不會發生級聯效應的，因為網絡規模夠大的話，一條邊的流量相對來說就比較小了所以不會造成損毀級聯效應。

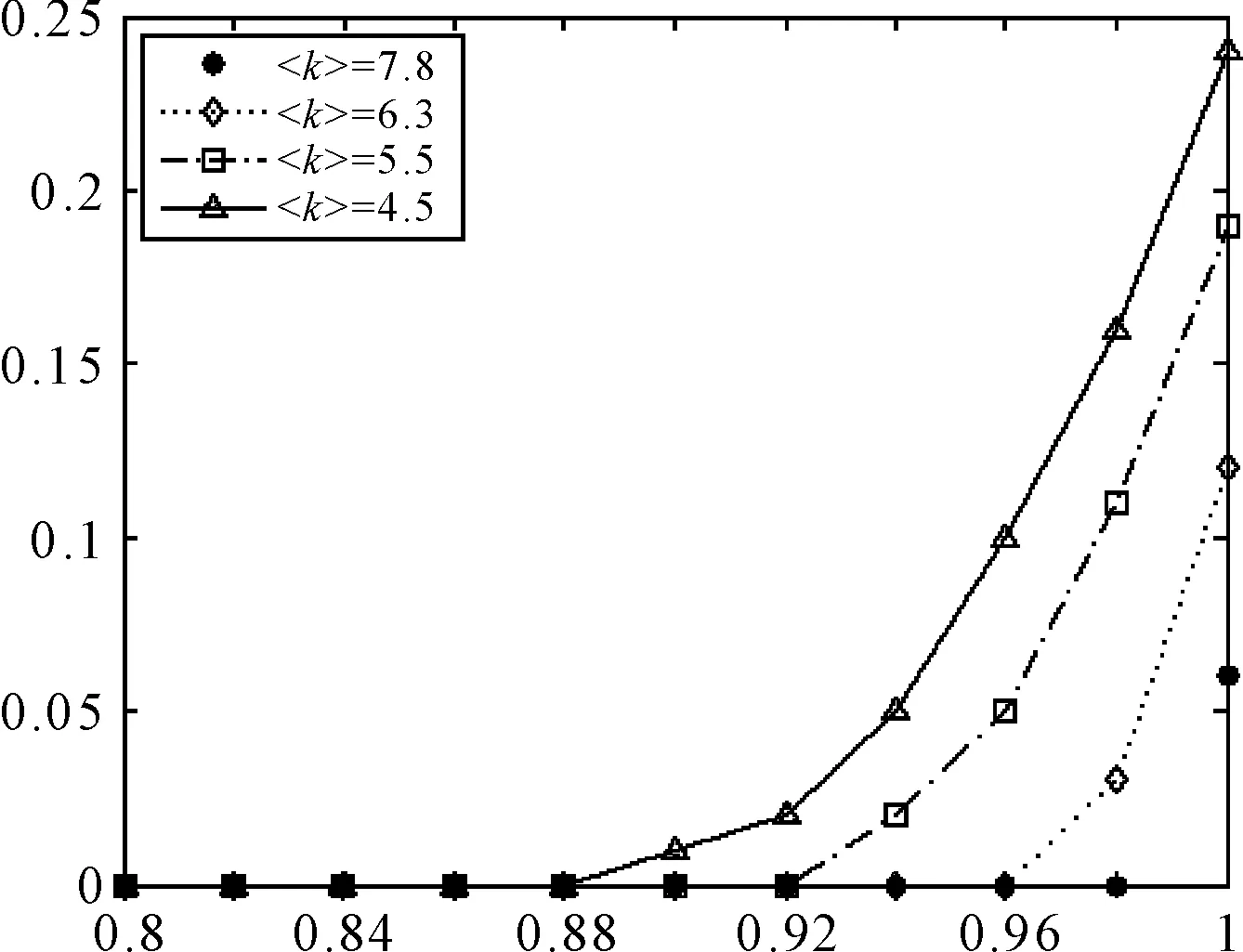
圖7　不同〈k〉值網絡仿真結果分析圖

平均度〈k〉減少為6.3、5.5、4.5后得到控制參數μ與損失比例R的關系隨〈k〉變化而變化，如圖7所示。隨著平均度〈k〉的減小，控制參數μ每增長一個步長，損失比例R會增加。綜合圖6和圖7可知，平均度〈k〉對網絡抗毀性所作的貢獻比控制參數μ的大。也就是說，對于網絡級聯失效抗毀性來說，網絡中互連邊的數量多少，比邊的負載率更加有意義。即在不考慮裝備保障物流其他指標(如駕駛員水平、路況)的情況下，不怕道路的通行率高，就怕可選擇的路不多。

5　結語

本文以艦艇裝備保障網絡為研究對象，對網絡中邊失效所引發的級聯失效進行分析，提出失效邊上的負載的分流機制，選取邊的介數以及網絡的平均度為仿真模型的參數，確立了網絡模型的評價指標。

運用Matlab軟件進行了一系列仿真實驗，實驗結果表明，控制參數μ與平均度〈k〉均能影響網絡級聯效應性。其中，平均度〈k〉對網絡抗毀性所作的貢獻比控制參數μ的要更大。即網絡中有更多的互連邊、網絡的復雜性更高，網絡級聯效應抗毀性越好。

[1] 王建,劉衍珩,梅芳,等.基于網絡擁塞的Internet級聯故障建模[J].計算機研究與發展,2010,47(5):772-779.

[2] 崔曉迪,穆東,王耀球.基于客戶需求的物流業務耦合系統的研究[J].北京交通大學學報,2008,7(2):42-47.

[3] Sch?fer M, Scholz J, Greiner M. Proactive Robustness Control of Heterogeneously Loaded Networks[J]. Phys. Rev. Lett.,2006,96(10):108-701.

[4] Li K, Gao Z, Mao B, A weighted network model for railway traffic[J]. International Journal of Modern Physics C,2006,17(9):1339-1347.

[5] Sen P, Dasgupta S, Chatterjee A, et al. Small-world properties of the Indian railway network[J]. Physical Review E Phys Rev E,2003,67(3):036106.

[6] 王建.現代物流網絡系統的構建[M].北京:科學出版社,2005.

[7] 種鵬云,帥斌,陳鋼鐵.恐怖襲擊下危險品運輸網絡級聯失效抗毀性建模與仿真[J].計算機應用研究,2013,30(1):107-110.

[8] Zheng, D.F. and Erg?n G.. Coupled growing networks[J]. Advances in complex systems,2003,6(4):507-514.

[9] 王建偉,榮莉莉.基于負荷局域擇優重新分配原則的復雜網絡上的相繼故障[J].物理學報,2009,58(6):3714-3721.

[10] Wang W X, Chen G. Universal robustness characteristic of weighted networks against cascading failure[J]. Physical review. E,2008,77(2):026101.

[11] 黃英藝.考慮級聯失效的物流網絡抗毀性研究[D].大連：大連理工大學,2014.

Analysis of Network Security Survivability of Warship Equipment Based on Edge Failure*

Warship equipment support network is a complex system which contains different kinds of nodes and complex routes. In the process of implementing the supporting plan, there will always be a road failure and congestion. Aimed at this problem, the edge failure load diversion mechanism, taking two factors including: the complexity of the network busy degree and network to network cascading invulnerability, and the simulation model is built to simulate the network. When complex network degree is lower and more busy, the network cascade failure survivability is worse. For network survivability, network complexity has a greater significance than network busy level.

warship equipment support, edge failure, cascading failure, network invulnerability

2016年2月10日,

2016年3月24日

張肖,男,碩士研究生，研究方向：軍事系統建模與運籌決策。

E273

10.3969/j.issn.1672-9730.2016.08.010