基于譜結構先驗的高光譜圖像受損譜段快速修復

劉　蕾閆敬文（.汕頭大學醫學院　廣東　汕頭　55063；.汕頭大學工學院　廣東　汕頭　55063）

基于譜結構先驗的高光譜圖像受損譜段快速修復

劉蕾1閆敬文2
（1.汕頭大學醫學院廣東汕頭515063；2.汕頭大學工學院廣東汕頭515063）

本文在分析高光譜圖像譜結構先驗的基礎上，結合經典Karhunen-Loève變換，提出了一種基于譜結構先驗的高光譜圖像受損譜段快速修復算法.該方法首先對高光譜數據進行分塊分組，然后對同一空間塊中相鄰的兩組數據分別進行KL變換，并通過相鄰組自適應保留的幾個最大特征值修復受損譜段.實驗結果表明該方法簡單易行，另外圖像所包含的紋理和邊界信息越豐富，恢復圖像的質量越高.

高光譜圖像；Karhunen-Loève變換；受損譜段

0　引言

高光譜遙感成像以其光譜分辨率高、圖譜合一的特點受到國內外研究者的廣泛關注.高光譜圖像在植被與土地資源信息提取與檢測［1-2］、地質［3］、大氣［4］、農業［5］及軍事［6］中有著極為重要的應用.短短二十多年，高光譜遙感無論在成像光譜儀等硬件方面還是在圖像處理系統等軟件方面都得到了的迅速發展.但是，由于傳感器的高敏感性、傳輸誤差以及大氣和水蒸汽對固定波段能量的吸收，使得在地面接收站收到的高光譜數據含有大量的噪聲，并且不同波段所含噪聲水平不盡相同，這將嚴重影響以譜分析為基礎的信息提取和分類等應用［7-9］.本文提出一種基于高光譜圖像譜結構先驗的高光譜圖像受損譜段快速修復算法.

1　高光譜圖像的譜結構先驗

高光譜圖像通過光譜成像儀獲取物體反射電磁輻射的連續光譜信息，得到一組3維立方體數據.同一組3維高光譜數據獲得的是相同空間位置不同光波頻率的立方體數據信息.由成像特點的限制，高光譜圖像含有基于兩種相關性的冗余信息［10］：1）譜間相關性，即每個譜段同一空間位置像素的相關性.2）空間相關性，即同一譜段圖像的某一像素與其相鄰像素的相關性.相關性分析是高光譜圖像分析的首要任務.高光譜圖像在譜間成像時，不同波段在同一空間位置成像組成光譜維數據.由于相鄰波段的波長接近，因此高光譜圖像具有較強的譜間相關性.假設高光譜數據X=（x（1），x（2），…，x（L））∈RM×N×L，其中x（i）表示第i譜段的圖像，M×N表示空間的維度，L表示高光譜數據的譜間維度.高光譜圖像的譜間相關性可以用圖像的互相關系數表示，定義如下：

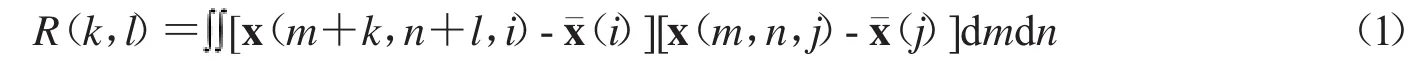
對公式（1）離散化和歸一化處理，得：

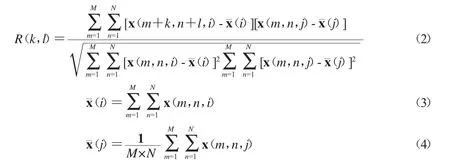
本論文選用美國AVRIS系統獲取的224譜段16 bit的3種類型的高光譜數據進行分析，數據通過http：//www.nasa.gov網站獲取，分別為植被（Moffett Field）、礦藏（Cuprite）和河流（Lunar Lake）3種類型的高光譜數據，其中Cuprite和Lunar Lake圖像紋理細節復雜.Moffett Field圖像紋理細節相對較少，圖像灰度值變化平緩，且紋理清晰簡單.針對這3種不同類型的數據，圖1給出了這3種類型的高光譜數據的譜間相關性曲線圖.由圖1可以看出，由于大氣和水蒸汽對固定波段能量的吸收，致使每一組高光譜數據均在105～111譜段，154～166譜段存在低相關性，數據信息受損嚴重.除此以外，其余各相鄰譜段間相關系數均在0.95以上，即譜間具有較強的相關性.究其原因，主要有以下兩點：

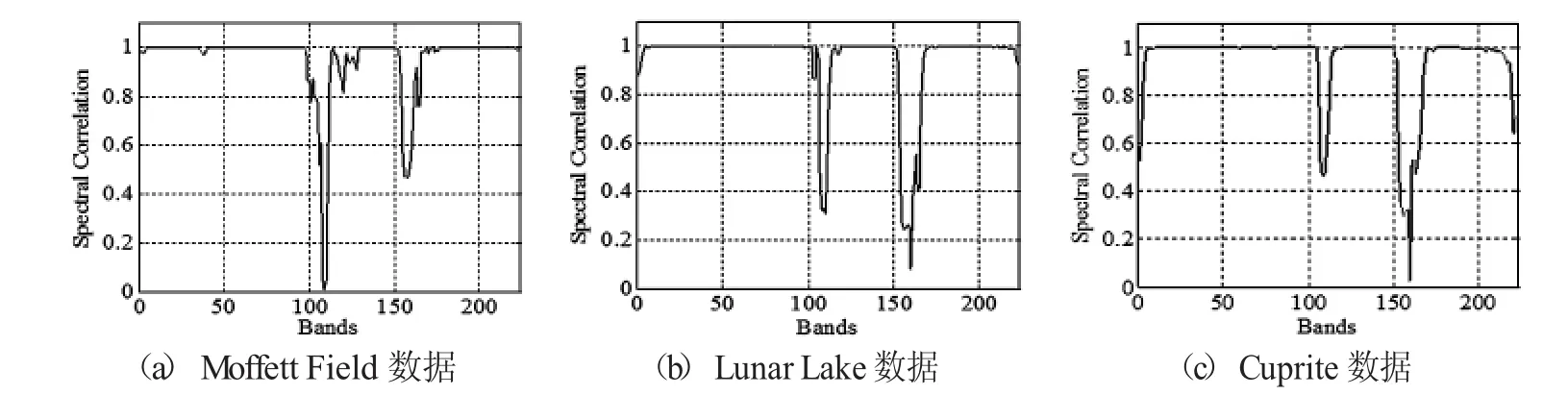
圖1　 3種類型高光譜圖像的譜間相關性

1）高光譜圖像是通過不同的波段對同一地區進行成像，成像地區具有相同的物理結構和特性，因此不同波段的成像圖像具有相似的輪廓，尤其是相鄰譜段間，這種相似性更為突出，這就導致相鄰譜段間圖像的相關性很高，這種相關性又稱為譜間結構相關性［11］.

2）譜段間的相關性受高光譜的分辨率影響，高光譜圖像的分別率越高，圖像像素值間的相關性越大，此相關性又稱為譜間統計相關性［11］，該相關性由傳感器的結構決定.

2　基于Karhunen-Loève（KL）變換的高光譜圖像快速去冗余算法

Karhunen-Loève（KL）變換是高光譜圖像壓縮中去除譜間冗余的經典算法［12-13］.KL變換是以圖像的統計特性為基礎的一種正交變換，它應用了本征矢量空間技術將變換的數據映射到本征矢量空間上，是在最小均方誤差的意義上的最優變換.沿著譜維度，KL變換使得編碼后數據的能量集中在少數幾個主成分上.KL變換對零均值數據的協方差矩陣進行特征值分解.零均值高光譜數據的協方差矩陣C按如下公式求得［14］：

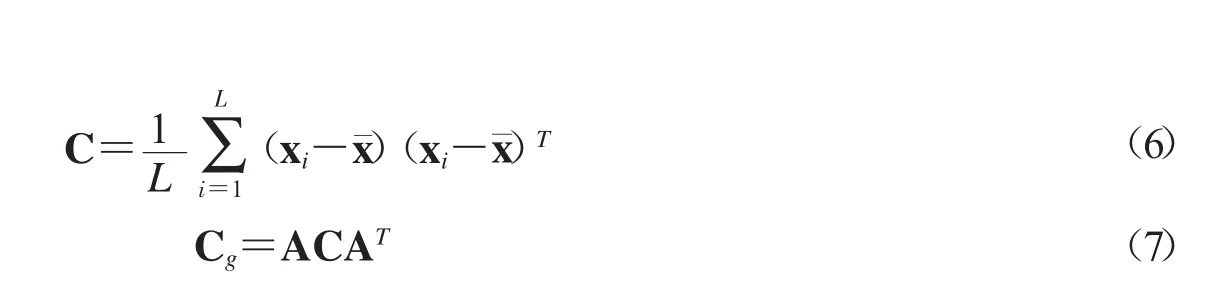
其中xi（1≤i≤L）表示高光譜圖像數據x第i譜段的空間圖像，表示高光譜數據x在譜方向的均值.通過對協方差矩陣C做特征值分解可以得到對角陣Cg，其對角線上的元素Cg（i，i）=λi（1≤i≤mn）表示特征值.A和AT表示規范化的正交特征向量和它的轉置矩陣.不同的高光譜數據會得到不同的規范化正交特征向量A.本文采用自適應選取KL分解的特征向量，要求按照以下公式保留的圖像能量不低于總能量的99%，

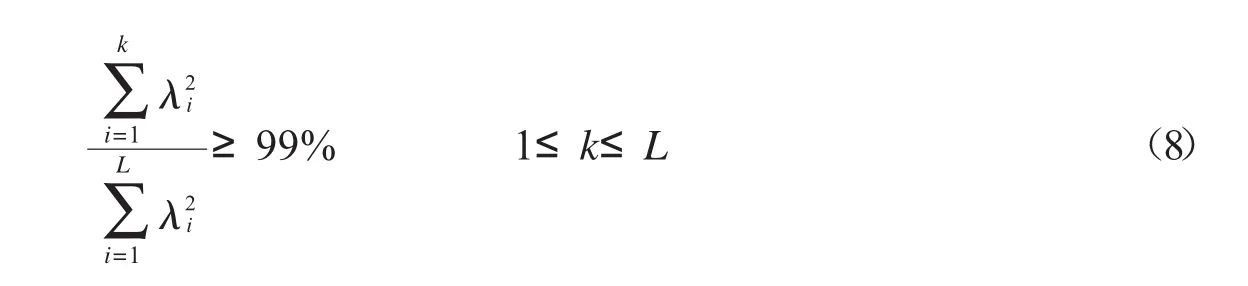
通過自適應選取特征值對應的特征向量，KL變換公式如下：

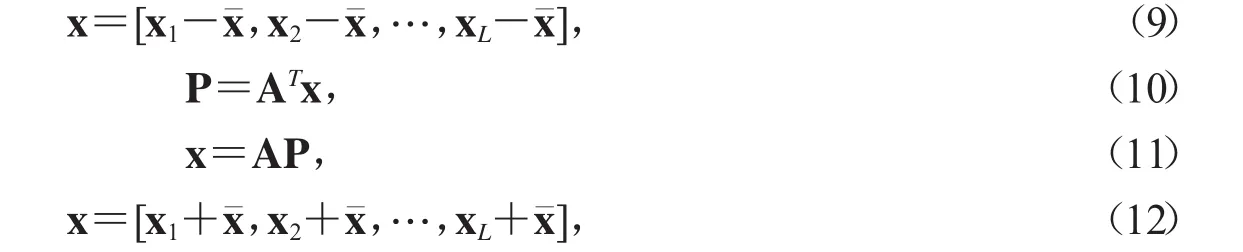
其中P表示零均值高光譜數據的KL變換矩陣，自適應選取特征值時，僅保留特征值對應的特征向量與零均值高光譜數據乘積的主成分.

3　基于譜結構先驗對受損譜段的修復

3.1交叉驗證

根據高光譜圖像的譜結構先驗，我們得到相鄰譜段之間的譜相關性接近于1.當變換圖像具有相同的空間位置（同一個patch塊）和不同的譜段分組（group）時，如圖2所示分組規律，我們是否可以通過保留前一組高光譜數據的變換矩陣恢復后一組高光譜數據？如果所提算法可行，當后一組高光譜數據中含有噪聲等受損譜段時，我們即可通過變換矩陣的替換操作能夠有效去除數據中所含噪聲.圖3給出了所提算法的交叉驗證試驗結果.在驗證實驗中，我們選取1～64譜段的Moffett高光譜數據作為測試數據，按照32個譜段分成一組，共分成兩組，其中數據的像素值規范化到0～1.由于高光譜數據在不同譜段所含噪聲的水平是不同的，因此，我們分別在第40譜段，41譜段和42譜段的高光譜圖像上增加了噪聲水平為0.02，0.04和0.08的高斯白噪聲，如圖3（d）-（f）所示.同時對兩組數據進行KL變換，我們保留第一組數據的變換矩陣，用來恢復第二組數據.由于高光譜數據進行KL變換后，特征值呈快速衰減的趨勢.當我們保留最大的1-2個特征值對應的特征向量及均值即可重構出該質量圖像.圖3（g）-（i）給出了恢復的圖像.可以看出，圖像紋理質量有了較大幅度的提升.

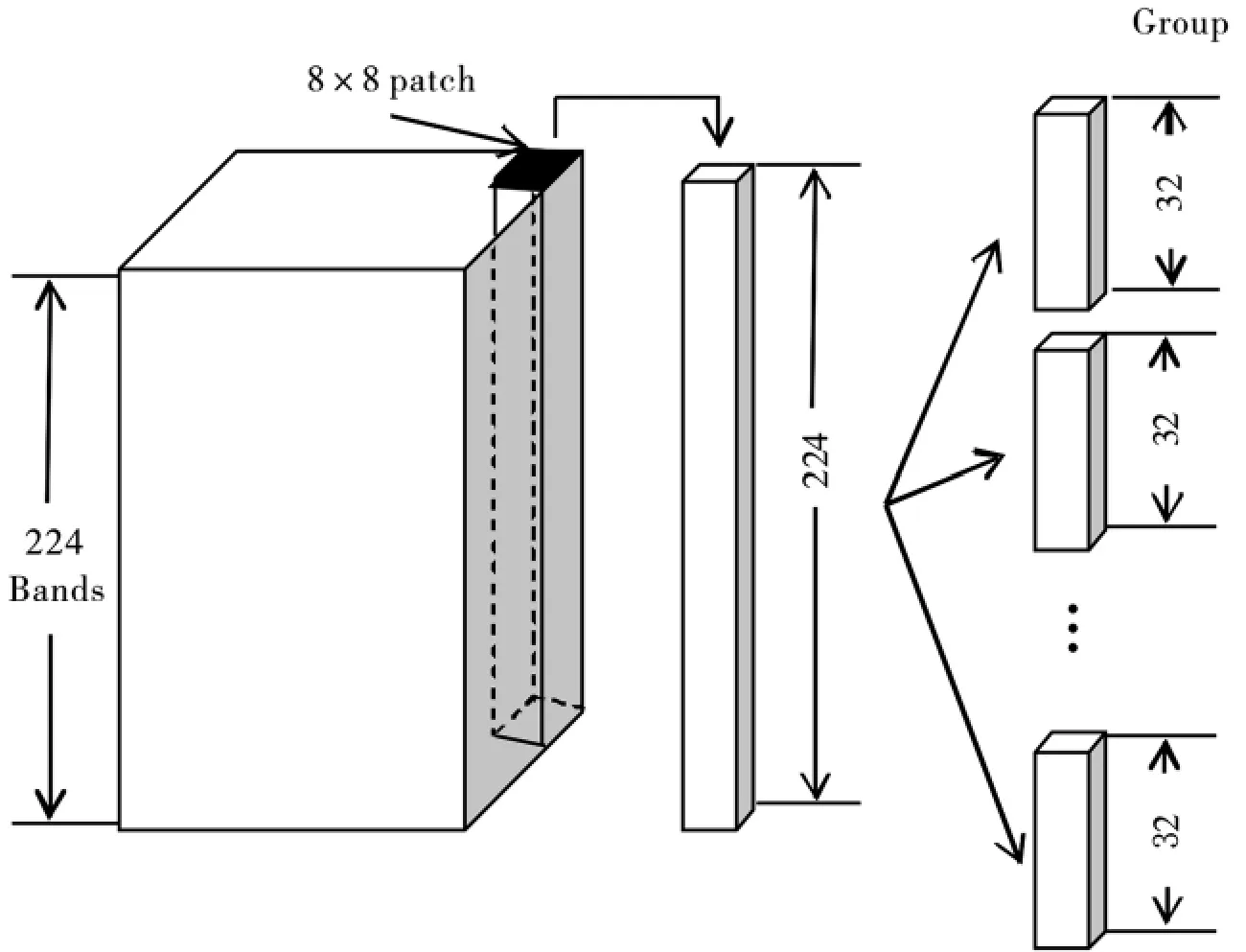
圖2　 224譜段高光譜數據分組

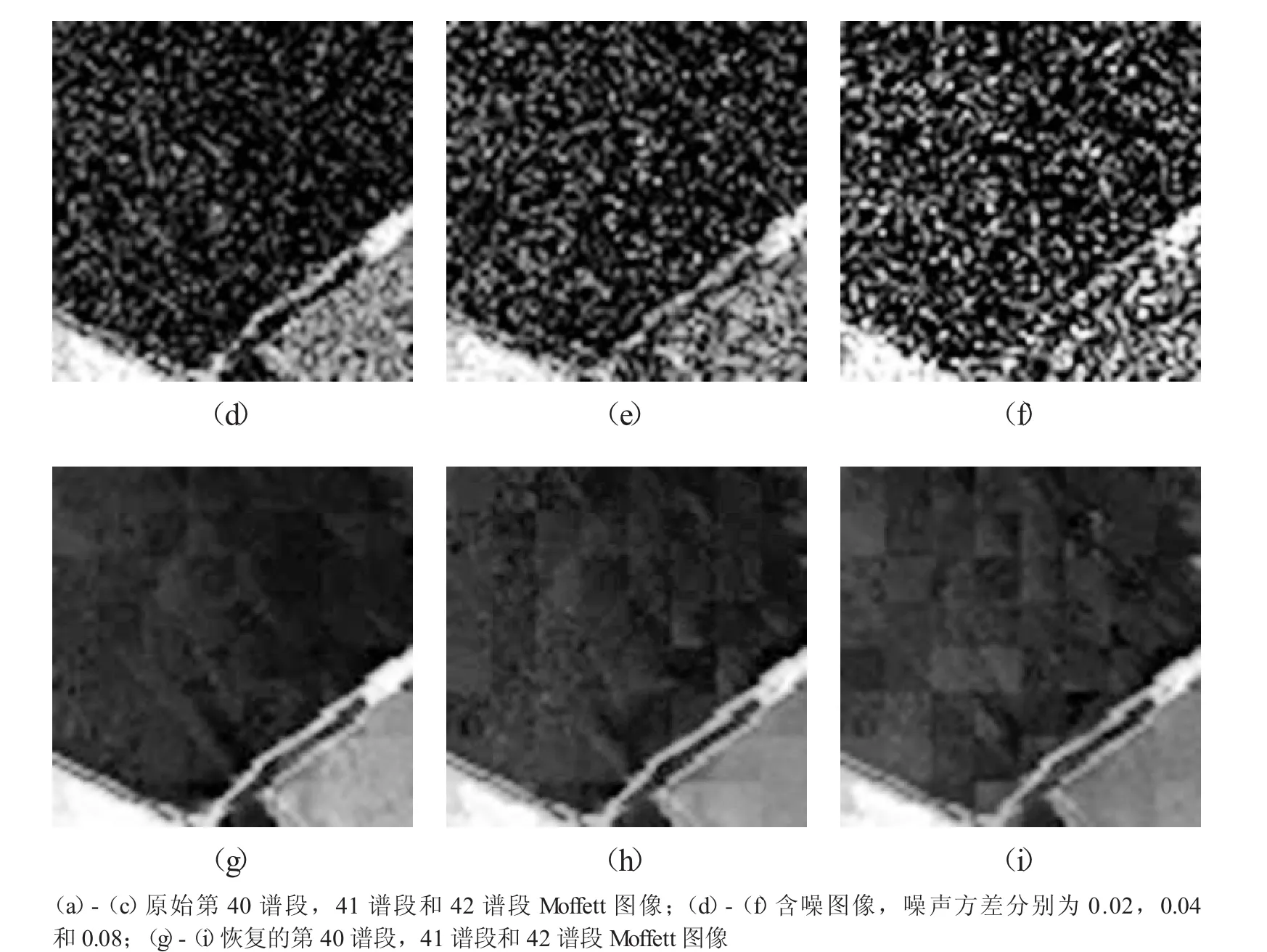
圖3　結構先驗去噪的測試與驗證

3.2譜段修復

通過以上交叉驗證實驗可以看出，利用譜結構先驗可以很好的修復高光譜數據中受噪聲污染的受損譜段.在實現的過程中，由于每一組數據KL變換的特征值均按照降序排列，因此對應得到的特征向量和主成分也均按照降序排列.應用該方法進行譜段修復時，我們只需自適應保留最大特征值對應的特征向量和主成分作為新的變換矩陣，算法總結如下.

Step 1：按照8*8空間大小對高光譜圖像分塊，每一塊包含所有譜段，數據大小為8*8*224.

Step 2：每一個空間塊再按照32譜段一組進行分組，每一組數據的大小為8*8*32.

Step 3：同一空間塊中相鄰的兩組數據，分別進行KL變換后，自適應保留前一組的最大幾個特征值所對應的特征向量和變換的主成分作為后一組重建的變換矩陣，由于相同空間位置的數據具有相同的譜結構，聯合后一組的譜均值一起來即可恢復后一組數據.

由于嚴重受損譜段是由于水蒸汽對固定波段能量的吸收而產生的，受損譜段區域較為固定.在有了這些先驗知識以后，我們較容易對受損譜段進行修復.圖4給出了利用自適應KL變換和譜結構稀疏先驗恢復的受損圖像.由圖4（d）-（f）可以看，該算法可以很好的修復高光譜數據中嚴重受損圖像，而且，圖像所包含的紋理和邊界信息越豐富，恢復圖像的質量越高.

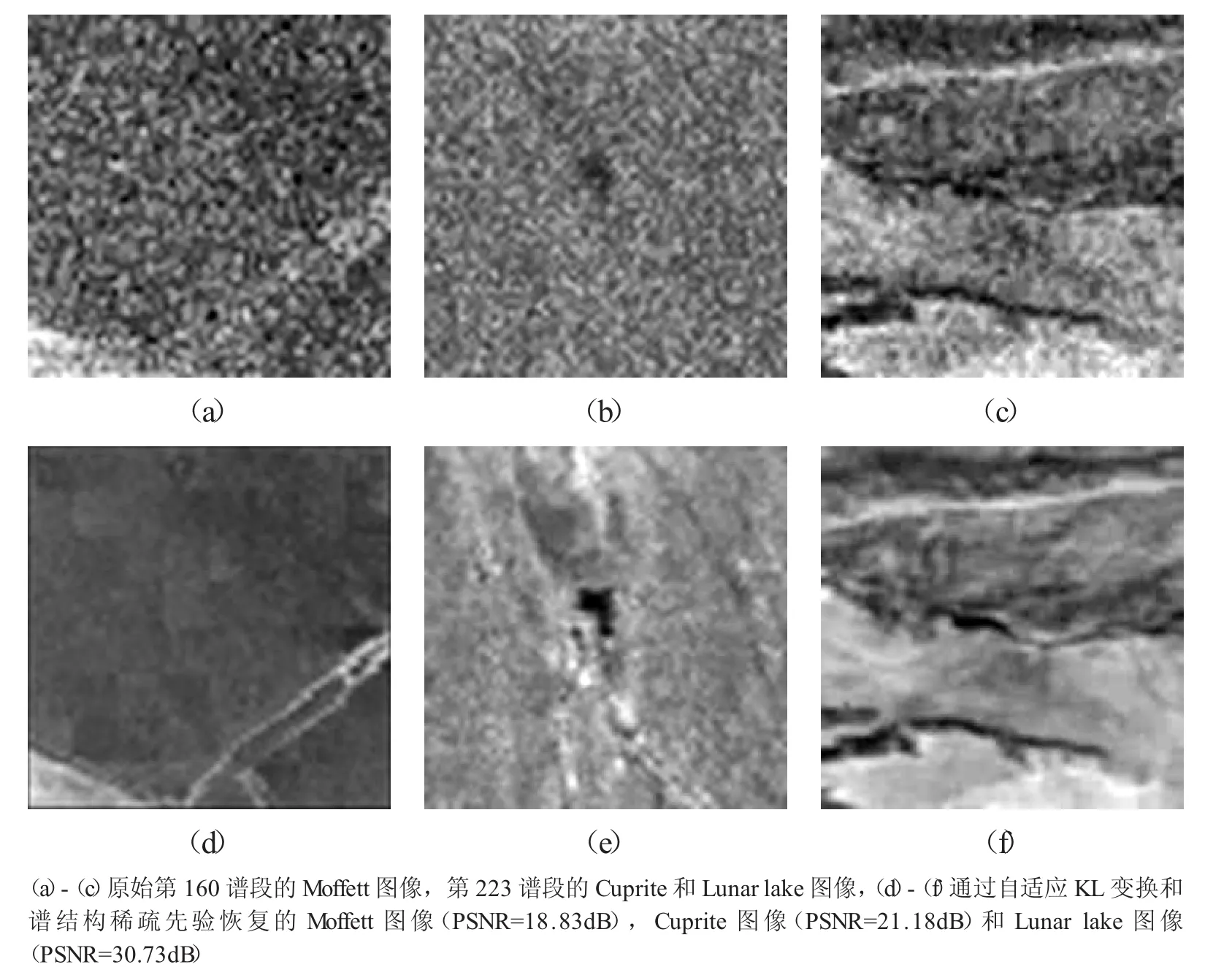
圖4　通過自適應KL變換和譜結構稀疏先驗恢復受損譜段

4　結論

基于譜分析的高光譜數據應用一直是高光譜研究的一個重點，然而，由于傳感器的高敏感性、傳輸誤差以及大氣和水蒸汽對固定波段能量的吸收而遭到嚴重破壞的受損譜段會制約譜分析的應用.本文提出了一種基于譜結構先驗的高光譜圖像受損譜段快速修復方法.實驗顯示，所提方法對受損高光譜數據都具有很好的修復性能，而且，圖像所包含的紋理和邊界信息越豐富，恢復圖像的質量越高.在后續的研究中，我們計劃設計更加有效地特征值分解方法，該方法不需要求出所有的特征值和特征向量，只需求出所需要個數的特征值進行快速成像.

［1］譚炳香.高光譜遙感森林類型識別及其郁閉度定量估測研究［D］.北京：中國林業科學研究院，2006.

［2］王靜.土地資源遙感與評價方法［M］.北京：科學出版社，2006.

［3］DEBBA P，CARRANZA E J M，VAN DER MEER F D，et al.Abundance estimation of spectrally similar minerals by using derivative spectra in simulated annealing［J］.IEEE Geosci Remote Sens.，2006，44（12）：3649-3658.

［4］MIURA T，TURNER J P，HUETE A R.Spectral compatibility of the NDVI across VIIRS，MODIS，andAVHRR：an analysis of atmospheric effects using EO-1 hyperion［J］.IEEE Trans.Geosci.Remote Sens.，2013，51（3）：1349-1359.

［5］RAN Q，LI W，DU Q，et al.Hyperspectral image classification for mapping agricultural tillage practices ［J］.J Appl Remote Sens，2015，9（1）：097298.

［6］ARDOUIN J P，LEVESQUE J，REA T A.A demonstration of hyperspectral image exploitation for military applications［C］.2007 10th International Conference on Information Fusion，9-12 July2007，Quebec.［S.L.］：IEEE，2007：1-8.

［7］ZHONG P，WANG R.Multiple-spectral-band CRFs for denoising junk bands of hyperspectral imagery［J］. Geoscience and Remote Sensing，IEEE Transactions on，2013，51（4）：2260-2275.

［8］LU T，LI S T，FANG L Y，et al.Spectral-spatial adaptive sparse representation for hyperspectral image denoising［J］.IEEE Transactions on Geoscience&Remote Sensing，2016，54（1）：373-385.

［9］ZELINSKI AC，GOYALVK.Denoisinghyperspectral imageryand recoveringjunk bands usingwavelets and sparseapproximation［J］.in 2006 IEEE IntGeosciRemoteSensingSymp（IGARSS2006），2006：387-390.

［10］劉恒殊，彭風華，黃廉卿.超光譜遙感圖像特征分析［J］.光學精密工程，2001（4）：392-395.

［11］陳雨時，王曉飛，張曄.基于特征變換的高光譜圖像壓縮快速矢量量化算法［J］.黑龍江大學自然科學學報，2008，25（3）：332-336.

［12］PENNA B，TILLO T，MAGLI E，et al.A new low complexity KLT for lossy hyperspectral data compression［J］.IEEE International Conference on，Geoscience and Remote Sensing Symposium，2006 （IGARSS 2006），July 31 2006-Aug 4 2006，Denver，Co，USA.［S.L.］：IEEE，2006：3525-3528.

［13］YANJ W，QUXB，CHENJ Z.Newquasi-lossless compression ofpartitioned KLTand IWT multispectral images［J］.Acta Optica Sinica，2007，27（10）：1740-1744.

［14］YAN J W，SUN H，ZHANG S H.A multispectral image data compression method based on KLT/DCT［J］. Chin J Lasers，1997，6（2）：110-116.

A Quick Repairment Method of the Junk
hyperspectral Bands Using Spectral Structure Prior

LIU Lei1YAN Jingwen2
（1.Medical College，Shantou University，Shantou 515063，Guangdong，China；2.College of Engineering，Shartou University，Shantou 515063，Guangdong，China）

Based on the analysis of the spectral structure prior of hyperspectral image，a quick repairment method for the junk hyperspectral bands with classical Karhunen-Loève transform is proposed.Firstly，hyperspectral image is divided into groups and blocks.For the two adjacent sets of data of the same space block，KL transform is used respectively.The junk bands are repaired with a few maximal eigenvalues of adjacent efficient block.The experiments show that our method is simple and effective.The texture and boundary information is richer and the quality of the restored image is higher.

hyperspectral image；Karhunen-Loève transform；junk bands

TP751.1

A

1001-4217（2016）02-0059-07

2015-12-30

劉蕾（1978—），女（漢族），河南省開封市人，博士.研究方向：稀疏表示，稀疏重建.

E-mail：wliulei@stu.edu.cn

閆敬文（1964—），男（漢族），吉林省磐石人，博士，教授，博士生導師.研究方向：稀疏表示，稀疏重建.

E-mail：jwyan@stu.edu.cn

廣東省數字信號與圖象處理技術重點實驗室開放基金資助項目（2015GDDSIPL-03）；廣東省自然科學基金資助項目（2015A030313654）