IncPR：一種基于增量計算的并行PageRank算法

姜雙雙　廖　群　楊愚魯　李　濤

(南開大學計算機與控制工程學院　天津　300350)

?

IncPR：一種基于增量計算的并行PageRank算法

姜雙雙廖群楊愚魯李濤

(南開大學計算機與控制工程學院天津300350)

(highfly@mail.nankai.edu.cn)

廣泛的互聯網的商業應用使PageRank算法有重要地位.網絡規模不斷地增大，同時網絡變化帶來的時效性要求，也使PageRank計算對計算資源的要求不斷地提高.為降低該問題對計算資源的消耗水平，降低計算成本，一種基于增量計算思想的PageRank算法：IncPR被提出.IncPR通過重用已有的結果，增量地獲得數據變化后的結果.該算法在并行計算環境中，能夠有效地降低計算量，縮短計算時間.理論分析表明，該算法計算結果的誤差范圍與蒙特卡羅PageRank算法相當，其時間復雜度優于其他已有的相關算法，且不引入額外的存儲開銷.在分布式集群Hama上進行的實驗驗證了理論分析的結果，IncPR在得到與蒙特卡羅PageRank算法同等(甚至更高)結果精度的情況下，顯著地降低了計算量.

PageRank；Web數據挖掘；增量計算；蒙特卡羅算法；并行與分布式處理

隨著電子商務、物聯網、社交網絡、生物信息學等諸多領域的蓬勃發展，大量有價值的數據快速地產生并積累，“大數據”的計算處理成為近年來的研究熱點之一.大量的統計結果顯示，大數據應用問題普遍具有數據的總量大且增長速度快的特點[1].截止到2016年3月，Google抓取的網頁已超過60萬億，并以每天超過450億個網頁的速度增長[2-3]；FaceBook的用戶數量已達到13億并保持每秒5位用戶的增長速度[4].當數據發生變化時，需要對數據重新處理以更新結果，因此，高效地處理頻繁變化的大數據具有重大意義.

PageRank[5]算法在搜索引擎、信息檢索、社交網絡挖掘等多個領域得到廣泛的應用，具有重要地位.PageRank算法所處理的互聯網絡和社交網絡數據是典型的頻繁變化的大數據集，具有總量大、更新速度快、每次更新的數據占總量比例小的特點.為滿足結果的時效性要求，只要數據更新就需要重計算以更新結果.在頻繁變化的大數據集上反復地進行PageRank計算，會消耗巨大的計算資源，計算成本高.

盡管以MapReduce[6],Spark[7]及Pregel[8]集群等為代表的分布式計算技術、以及很多并行PageRank算法[9-11]能夠提高PageRank的計算速度.但這些技術仍不能有效地降低反復計算帶來的高資源消耗和高計算成本.

因此針對這一問題本文通過擴展一種典型的PageRank計算算法——蒙特卡羅算法[12]，提出了一種基于增量計算的PageRank算法——IncPR.當數據集發生變化時，IncPR利用的是已有的PageRank計算結果，不需要保存其他歷史數據，沒有引入額外的存儲開銷；在進行處理時，IncPR根據數據的變化情況在已有的計算結果上增量地進行更新，獲得新數據集的結果，這有效地降低了計算量，提高了計算效率.此外，IncPR能高效處理網頁增加、減少、網頁鏈接關系變更等多種情況，這也是其較之于部分相關增量算法的優勢之一.

理論分析證明，IncPR得到結果的誤差范圍和蒙特卡羅PageRank算法得到的結果誤差范圍的量級相當，即IncPR具有與蒙特卡羅PageRank算法相同的正確性.在增加m個節點和n條邊的情況下，IncPR的時間復雜度為O((cm+n)Rc2)，其中參數c和R分別代表蒙特卡羅方法的停止概率和啟動次數.IncPR的時間復雜度優于其他已有的增量PageRank算法.在分布式集群Hama[13]上進行的實驗驗證了理論分析的結果，實驗數據表明在得到與蒙特卡羅PageRank算法同等(甚至更高)精度結果的情況下，IncPR顯著地降低了計算量.

綜上，本文工作的貢獻有3點：

1) 提出了一種基于增量計算的PageRank算法IncPR.通過在已有結果的基礎上，增量地更新得到新結果的方法，IncPR能有效地降低PageRank的計算量，且不引入額外的存儲開銷；

2) 通過理論分析證明了IncPR與蒙特卡羅PageRank算法的結果具有相等量級的精度，且時間復雜度優于已有的增量PageRank算法；

3) 在Hama集群上基于大規模真實圖數據的大量實驗，驗證了IncPR的正確性和計算效率.IncPR在保證結果正確的前提下能有效降低PageRank的計算量.

1　相關工作

1.1PageRank算法

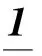
P=(1-c)Q+(cn)E；

(1)

(2)

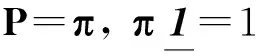
(3)

當前PageRank算法主要可以分成2類：線性代數方法和蒙特卡羅方法.前者利用線性代數方法根據式(3)求解π,PowerIteration[5]、Gauss-Southwell[14]、基于LUQR分解的PageRank算法[15]等是典型的線性代數計算方法.它們處理大規模矩陣效率高，且能夠根據需要權衡結果精度和計算開銷.蒙特卡羅方法[12,16-17]的基本思想是利用隨機游走模擬大量用戶隨機訪問網頁的行為，并通過統計各節點的被訪問次數估算PageRank的近似值.典型的蒙特卡羅方法[12]包括循環起點的全路徑算法、隨機起點的蒙特卡羅算法等.它們具有易于并行化的特點，且能夠以較小的計算開銷盡快地得到滿足精度要求的近似結果.

相關的研究結論已證明[12]相較于其他蒙特卡羅算法，循環起點的全路徑蒙特卡羅算法具有更高的計算效率，因此在已有PageRank算法優化研究[18]中常被作為算法改進的基礎.該算法的計算方法更適于引入增量計算的思想.本文工作也將循環起點的全路徑算法作為蒙特卡羅算法的代表，簡稱為基準蒙特卡羅算法，用BasicPR表示.BasicPR計算PageRank的方法是由每個節點為起點啟動R個隨機游走過程，隨機游走中的每一步以c的概率停止或走到等概率地隨機選中的某個鄰居節點，并以此選中的節點為起點繼續這個隨機游走過程.對于有n個網頁的情形，共進行n×R次隨機游走，當所有隨機游走過程都停止時，統計任意節點u的訪問次數VT(u)，用VT(u)除以所有節點的訪問次數的總和，就得到節點u的PageRank的近似結果.通過增加R，BasicPR的結果可以足夠接近PageRank的真實值.IncPR使用了和BasicPR相同的隨機游走方法并在其基礎上引入了增量計算思想加以改進.

1.2增量PageRank算法相關研究

為保證頻繁變化的網絡上獲得滿足時效性要求的PageRank值，通常需要反復進行PageRank計算，從而造成對計算資源的巨大消耗.為解決這一問題，一些改進的PageRank算法被提出.這些算法大致可以被歸納為4類:

1) 利用已有結果加速迭代收斂

Kamvar等人[19]提出了一種基于AitkenΔ2的推斷方法加快收斂的算法,該算法的收斂效率受變化數據位置影響，效率的提升并不明顯[18].Ohsaka等人[14]提出了一種通過重用已有結果的Guass-Southwell方法，該方法能夠提升算法的收斂速度，但該算法并沒有討論節點變化的情況的處理方法.

2) 控制及利用變化的數據的影響范圍

此類算法[20-23]通常將整個圖按照某種策略劃分成若干相互連通的子圖，當某個子圖內發生變化時，算法盡量將計算操作控制在子圖內部，對其他子圖不產生影響或影響較小，從而達到降低計算量的目的.它們的局限性在于算法的表現受圖結構的影響較大，且維護有效的圖劃分也比較困難.

3) 基于蒙特卡羅方法的增量改進

與線性代數方法相比，蒙特卡羅方法顯然更易于按照增量計算的思想進行改進[12].Bahmani等人提出算法[18]保存之前的隨機游走路徑，當數據發生變化時，根據圖的變化情況對隨機游走路徑進行部分更新.Bahmani的算法假設圖中的邊隨機地逐條到達，每當一條邊到達即進行計算，當累計增加n條邊時，處理包含|V|個節點的圖數據，該算法的時間復雜度為O(|V|lnnc2).Lofgren等人[24]在Bahmani等人工作[18]的基礎上，對算法復雜度的分析進行了補充.該算法是一種高效的增量PagaRank算法，能有效應對節點和邊發生變化的情況，但其保存隨機游走路徑的歷史數據的做法也引入了較大的存儲開銷.

4) 其他方法

Tong等人[25]提出了一種適合于二分圖的更新PageRank值的方法，該方法在|V|×l的圖上能夠獲得O(l2)的時間復雜度，然而互聯網和社交網絡中的l=|V|，當n條邊到達時，更新的代價為O(n|V|2)，并不適合擴展到大規模圖數據中來.Mcsherry等人[26]將多種啟發算法應用到迭代算法中，以增量的更新操作計算流數據上的PageRank值，但該算法在控制計算量的情況下不能保證結果精度.

綜上，已有的增量PageRank算法，都需要消耗額外的存儲空間.本文提出的IncPR并不需要額外的存儲空間，且相較于已有的高效增量PageRank算法，IncPR的時間復雜度更低，在計算效率和存儲開銷2個方面優勢明顯.

2　增量PageRank計算模型

為降低頻繁變化的海量數據集上反復計算PageRank的資源消耗，節約計算成本，本文提出了一種增量PageRank算法——IncPR.本節首先以一個示例介紹基于增量計算思想的PageRank計算方法，接著給出IncPR的計算模型的形式化概述.

2.1增量PageRank計算示例

增量PageRank計算將每一次數據更新作為一個新時刻.假設時刻t圖G形如圖1(a)所示，其中實線表示時刻t-1的圖數據，虛線表示的邊e3,5是在時刻t新增加的.圖1(b)表示時刻t-1使用BasicPR得到的隨機游走路徑的集合.

在使用BasicPR計算時刻t的圖數據時，節點5在隨機游走中被訪問的機會較時刻t-1增大.如果以圖1(b)所示的隨機游走路徑當作時刻t的初始路徑，那么僅需要更改部分路徑(每次訪問節點3后的隨機游走路徑)即可以得到符合時刻t各節點的被訪問概率的隨機游走路徑.即每當遇到隨機游走路徑中出現節點3，即按照時刻t的圖，為節點3重新選擇下一步的節點，并更新之后的隨機游走路徑.這樣即可得到如圖1(c)所示的隨機游走路徑.盡管這個集合是由圖1(b)變化來的，但該集合中各節點被訪問的概率和在時刻t的圖上重新產生的隨機游走路徑集合相等，其概率都是由圖的拓撲特征和隨機游走的停止概率參數共同決定的.

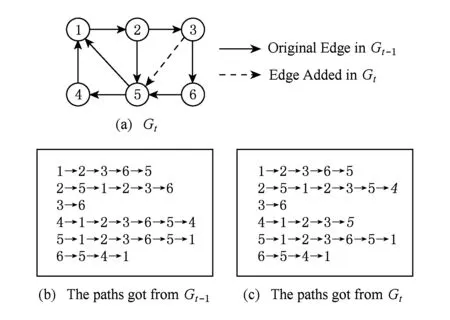
Fig. 1　An example of computing PageRank incrementally.圖1　增量PageRank計算示例

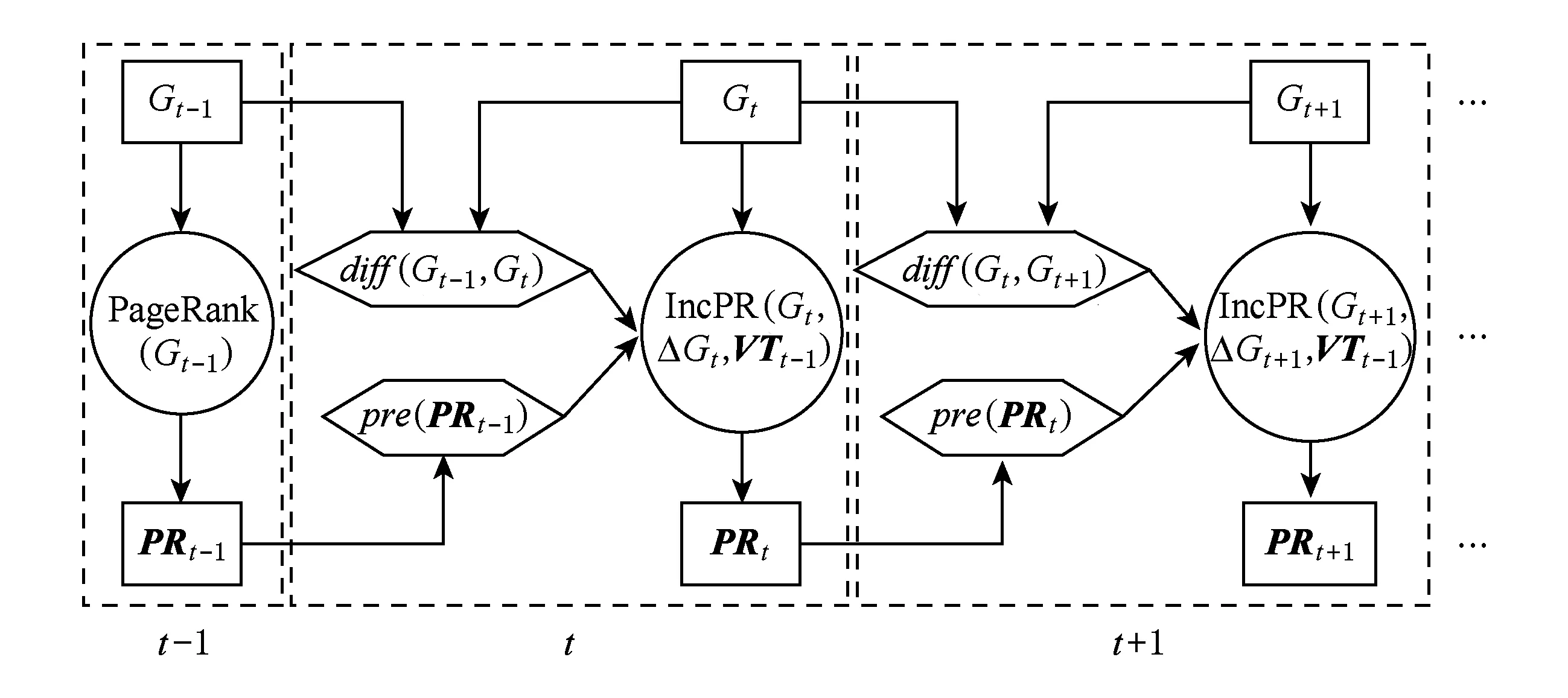
Fig. 2　Overview of incremental computation of PageRank.圖2　增量PageRank計算模型

基于這種考慮，就可以將增量計算的思想引入PageRank的計算過程.以時刻t-1的BasicPR得到的隨機游走路徑為基礎，在發生變化的邊(或節點)所影響的路徑上采用相同的隨機游走過程更新隨機游走路徑，并重新計算PageRank得到新結果.這樣的增量計算方式，避免了重新從頭生成全圖的隨機游走路徑，降低了計算量.這也是已有的基于蒙特卡羅方法的增量PageRank算法[12,18,24]的基本計算過程.此類算法能夠降低PageRank的計算量，但需要較大的存儲開銷來保存隨機游走路徑.

而從節點的訪問概率的角度觀察，對時刻t的圖進行計算時，與時刻t-1相比，每次訪問節點3后，節點5被訪問的概率增加，節點6被訪問的概率減少，而且節點5被訪問的概率的增加量和節點6減少的量基本相當.這一特點即是IncPR的設計基礎之一.

2.2增量PageRank計算模型概述

IncPR是一種基于增量思想的PageRank算法，易于并行化實現.與已有的基于蒙特卡羅算法的增量PageRank算法不同，IncPR并不需要保存任何隨機游走路徑的歷史信息.它利用之前一個時刻已經得到的PageRank向量，逆推得到蒙特卡羅模擬的節點訪問次數統計，結合圖數據的變化情況，增量地更新得到新圖上的節點訪問次數統計，進而更新PageRank的計算結果.

IncPR的計算過程借助于這樣的事實，即蒙特卡羅算法中節點的訪問次數的期望具有穩定性[11]，來保證其正確性(相關證明見4.1節).IncPR的計算過程本質上與2.1節中的增量計算過程類似，即以受增量影響的任意節點v為起點，生成若干新路徑片段，并用新路徑片段替換舊路徑片段的過程.

IncPR能有效地處理圖中節點和邊的增加與刪除的情況，且由于能較大程度地利用之前的結果，降低重復計算，因此該算法能夠有效地減少圖數據變更后重計算PageRank值的計算量.

IncPR在變化的圖數據上進行增量的Page-Rank計算的過程，可以形式化地描述為以下的增量計算工作模型，如圖2所示.對于圖G(V,E),令時刻t圖的快照為Gt(Vt,Et).圖的變化部分ΔGt=diff(Gt-1,Gt)={ΔVt,ΔEt}.相應地，從Gt得到的PageRank結果記作PRt.IncPR假設ΔGt已知，PRt-1已知，并通過預處理操作pre(PRt-1)得到BasicPR處理Gt-1時得到的所有節點的訪問次數的集合VTt-1.

IncPR算法以Gt,ΔGt和VTt-1為輸入，在VTt-1的基礎上，結合Gt,ΔGt采用改進的蒙特卡羅方法增量地更新ΔGt對于PageRank新值的影響，最終得到新的PageRank計算結果PRt.一般使用Xt代表符號X在時刻t對應的對象集合，而使用|X|代表集合X的元素的個數.

VTt=SVTt×PRt.

(4)

預處理可以按照式(4)的方式求得VTt-1.其中，SVTt是時刻t的蒙特卡羅模擬中所有節點訪問次數的總和，SVTt=|Vt|Rc.值得注意的是，式(4)具有普遍性，即使PRt-1并不是通過蒙特卡羅方法得到，也可以通過式(4)得到VTt-1.也就是說IncPR可以利用任意PageRank算法得到的結果.

3　IncPR：增量PageRank算法

IncPR通過重用當前已有的計算結果初始化節點的訪問次數，根據圖數據的變化對最終結果進行計算.對于圖數據變化的不同情況，采用不同的計算策略.本文將圖的變化分為2種情況：1)邊的變化,僅有邊的增加和刪除；2)點的變化,節點和邊均有增加和刪除.本節將分別介紹對這2種情況的處理方法.

3.1IncPR處理邊的變化

IncPR處理邊的變化時采取2個主要步驟:

1) 對于每條變化的邊，按一定策略更新某些節點的訪問次數；

2) 訪問次數被更新的節點，按照訪問次數的更新量進行若干次隨機游走，將新生成的隨機游走路徑上的節點的訪問次數(依據一定的原則)增或減1.

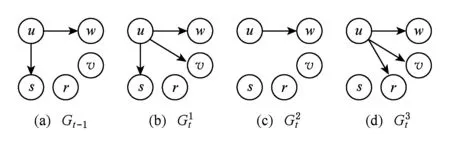
Fig. 3　Three cases of changing edges.圖3　邊變化的3種情況

圖3展示了一個節點上邊的變化的3種典型情況(與邊的變化無關的節點和邊被省略)，圖3(a)表示時刻t-1的圖數據Gt-1.圖3(b)(c)(d)表示時刻t的圖數據Gt，分別描繪了增加一條邊、刪除一條邊、同時增加刪除多條邊的示例.

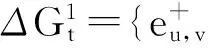
為了利用時刻t-1的訪問次數得到時刻t的結果，節點v的訪問次數需要加上期望的變化量，節點w,s的訪問次數平均分攤VT(v)t的增加量，作為各自訪問次數的減少量.當VT(v)t,VT(w)t和VT(s)t都更新完畢，則按照步驟2操作，s,v和w分別進行與各自訪問次數更新數量相等的隨機游走，從v發出的新隨機游走路徑上的節點的訪問次數增1，表示新路徑的添加；從s和w發出的新隨機游走路徑上的節點將訪問次數減1，表示舊路徑的刪除.上述操作的結果等價于經過節點u的部分路徑被新路徑替換.總體上看，上述操作相當于由于邊的增加，以s,v和w三節點為起點的隨機游走路徑中，從u獲得的訪問次數的重分配，重分配的結果與在圖Gt上重新進行隨機游走分配節點u發出訪問的情況相當.

邊刪除情況與邊增加情況的處理辦法類似.區別僅在于訪問次數的增減數量和操作順序.如圖3(a)(c)所示，當邊eu,s被刪除時，節點s的訪問次數VT(s)t減少，減少量的期望等于(1-c)×VT(u)t-1|S(u)t-1|,相應的節點w的訪問次數VT(w)t增加，增加量的期望等于VT(s)t的減少量.之后，分別以w,s為起點進行對應數量的隨機游走，來更新節點w,s的變化對其子節點的影響.以w,s為起點的隨機游走經過的節點分別進行加1和減1的操作表示新路徑的生成和舊路徑被替換.

結合邊的增加和刪除的情況，可以得到更一般化的處理方法.令eu,x表示變化(增加或刪除)的邊，M代表VT(x)t變化量的大小,對于u的其他鄰居y，令N代表VT(y)t變化量的大小，如式(5)(6)所示:

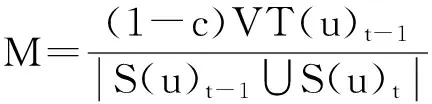
(5)

(6)

圖3(d)反映了在時刻t分別增加和刪除多條邊的情況.由蒙特卡羅方法的計算特點可知，多條邊分別增加和刪除的情況，可以視作多次發生增加單條邊和刪除單條邊的情況，按照上述處理單條邊增加和刪除的辦法依次處理即可.

算法1使用偽代碼描述了IncPR針對圖中邊的變化的處理邏輯.

算法1.ProcessIncEdges(Gt,diff(Gt-1,Gt),VTt-1,c).

輸入：Gt={Et,Vt}表示時刻t的圖數據、diff(Gt-1,Gt)={diff(E)+,diff(E)-}代表時刻t-1到時刻t圖數據的變化量(邊的增加和刪除)、VTt-1代表時刻t-1的節點訪問次數的集合、c是隨機游走的停止概率；

輸出：VTt為圖Gt的節點訪問次數的集合.

① 初始化VTt=VTt-1;

②ListSRW_Array〈node,count,tag〉;

③foreu,v∈diff(Gt-1,Gt)do

④ 由式(5)(6)計算M,N；

⑤ifeu,v∈diff(E)+do

⑥ SRW_Array.add(v,M,+);

⑦forw∈S(u)t-1do

⑧ SRW_Array.add(w,N,-);

⑨endfor

⑩else

3.2IncPR處理點的變化

節點的增加通常伴隨邊的增加，可分為新增節點有入邊和無入邊2種情況討論.如果新增加的節點沒有入邊，則只要按照與時刻t-1相同的隨機游走方法補上R次以新節點為起點的隨機游走，再更新節點的PageRank值即得到最終結果.但如果新增節點有入邊，則需要在上述處理的基礎上按照3.1節的方法處理.如圖4所示，圖4(a)(b)分別表示時刻t-1和時刻t的圖數據，這種情況可以視作2個過程的疊加：先增加一個節點和節點的出邊，得到如圖4(c)所示的過渡圖數據和對應的PageRank結果；再增加節點的入邊.

Fig. 4　An example of disassembly of adding a node.圖4　節點增加等價于節點和邊分別增加

類似地，節點的刪除則可以看作2個過程：節點的刪除和與節點相連邊的刪除.而稍有不同的是，對于刪除節點的情況，只需對變化的邊按照3.1節中的方法處理，而不需要再重復地減去R次以被刪除節點為起點的隨機游走對其他節點的影響，這個操作的影響在處理被刪除的邊時已被處理.

綜上，本文提出的IncPR可以概括為2個步驟：1)處理新增節點和節點的出邊；2)按照3.1的方法處理變化的邊.算法2為IncPR的偽代碼描述.

算法2.IncPR(Gt,diff(Gt-1,Gt),VTt-1,c,R).

輸入：Gt={Et,Vt}表示時刻t的圖數據、diff(Gt-1,Gt)={diff(E)+,diff(E)-,diff(V)+,diff(V)-}為時刻t-1到時刻t圖數據的變化量(邊和節點的增加和刪除)、VTt-1為時刻t-1得到的被訪問次數的集合、c是隨機游走的停止概率、R是各節點開始的隨機游走次數;

輸出：PRt為圖Gt的PageRank向量.

① 初始化VTt=VTt-1;*新增節點的訪問次數為0*

②foru∈diff(V)+do

③ count=R;

④whilecount>0do

⑤ 以u為起點進行停止概率為c的隨機游走，得到隨機游走路徑L;

⑥ 對任意節點yinL，VT(y)t++;

⑦ count--;

⑧endwhile

⑨endfor

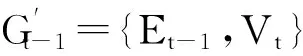
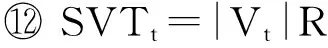
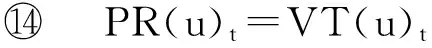
4　算法正確性及時間復雜度分析

4.1算法的正確性證明

IncPR是一種增量的蒙特卡羅模擬算法，基于模擬的PageRank算法得到的結果是近似值.類似于文獻[11,18]中對BasicPR正確性的證明，本文證明了IncPR與BasicPR計算得的節點的訪問次數的期望相等且IncPR計算得到節點的訪問次數與真實的訪問次數足夠接近,這樣即證明IncPR是正確的.

定理1. 對于任意節點v, 在圖Gt上使用IncPR得到的訪問次數的期望E[VT(v)IncPR]，與使用BasicPR計算得到的訪問次數的期望E[VT(v)BasicPR]相等.

證明.IncPR在進行計算時，利用圖Gt-1的訪問次數初始化Gt中節點的訪問次數，初始化的結果可以看作是從|Vt-1|個節點出發每個節點進行R次隨機游走得到的|Vt-1|R條路徑.對于每一個變化的邊eu,v，IncPR會從節點u的子路徑中選出M條舊的子路徑，并生成M條新的子路徑替換舊路徑.此操作并沒有改變總路徑的起點和數量；對于每個變化的節點，IncPR沿用BasicPR從每個節點進行R次隨機游走.因此，IncPR處理完Gt后，可以看作得到與BasicPR起點相同且對應起點數目相同的路徑.

使用BasicPR計算圖Gt的PageRank值時，圖中任意節點v的訪問次數的期望為

(7)

其中，Pu,v表示以節點u為起點的隨機游走路徑經過節點v的概率，αu表示以節點u為起點的隨機游走次數，由于2種算法每個節點都進行了R次隨機游走，故任意節點u的αu=R.從節點u出發的隨機游走路徑經過節點v的概率Pu,v是由每一條從節點u到節點v的路徑的概率累加得到的，如式(8)所示:

(8)

其中,qi j(i=u,w,…,y;j=w,x,…,v)如式(2)所示，表示節點u到節點w的跳轉概率，節點u選取某一條路徑訪問節點v的概率為該路徑上從u到v經過的節點間的跳轉概率的乘積.BasicPR在進行隨機游走時，任意節點間的跳轉概率只與圖結構有關，若節點u，w之間存在連邊，則qu,w=(1-c)|S(u)|；IncPR在進行隨機游走時，對于出邊發生變化的節點u，該節點的訪問次數按照期望值在子節點之間均勻分配，節點u到任意子節點的跳轉概率為(1-c)|S(u)|，這些節點與子節點間的跳轉概率與BasicPR中的相同；其他節點間的跳轉概率按照qu,w進行處理，與BasicPR相等.因此，IncPR在得到|Vt|R條路徑時，任意節點間的跳轉概率均與BasicPR相同.2種算法在計算圖Gt的PageRank值時，任意節點間的Pu,v相等.

綜上，IncPR算法與BasicPR在計算相同圖數據的PageRank值時，任意節點的訪問次數的期望相等，定理1得證.

證畢.

定理2. 對于任意節點v, 在圖Gt上使用IncPR得到的節點v的PageRank值與節點v的PageRank的真實值非常接近，即有式(9)成立:

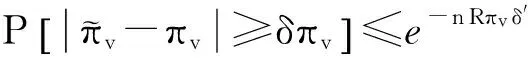
(9)

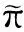
證明. 先討論R=1的情況(R>1的情況同理可證).假設隨機變量Xu是由u出發的隨機游走路徑上節點v的訪問次數的c倍.Yu是這條隨機游走路徑的長度.令Wu=cYu，xu=E[Xu].由于對于不同的節點u隨機變量Xu相互獨立，則有：

(10)

顯然有：0≤Xu≤Wu，E[Wu]=1.

則由期望的定義可知：

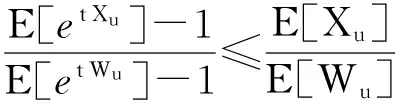
(11)

進而得到：

E[et Xu]≤xuE[et Wu]+1-xu=

xu(E[et Wu]-1)+1.

(12)

由于對任意的y有1+y≤ey，因此可得到：

E[et Xu]≤e-xu(1-E[et Wu]).

(13)

由馬爾可夫不等式，可以得到：

(14)

類似地可以證明：

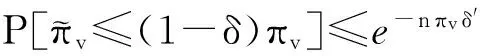
(15)

則定理2得證.

證畢.

綜合定理1，2可知，IncPR得到的計算結果能夠確保與BasicPR得到的結果同等正確.BasicPR計算PageRank的結果正確性在文獻[12]中已被證明，因此IncPR也具有與BasicPR同等的正確性.

4.2算法的時間復雜度分析

本節通過分析IncPR的處理過程，推導出其時間復雜度.使用IncPR計算PageRank向量時，對于每一個增加的節點，算法都會以該節點為起點進行R次隨機游走；對于每一個變化的邊eu,v，都會以v為起點進行M次隨機游走，作為新的子路徑；同時，會以u的其他子節點為起點進行M次隨機游走，作為待被替換子路徑.一條變化的邊需要進行2M次隨機游走，以更新結果.

因此，假設Gt在Gt-1的基礎上增加了m個節點且增加和刪除了共計n條邊，則增量算法需要進行隨機游走的總次數TotalRW滿足式(16)，其中M按式(5)求得.

(16)

令TotalComp表示IncPR的計算量大小，則有式(17)，其中E[X]代表隨機游走路徑長度的期望值.

TotalComp=TotalRW×E[X].

(17)

由于圖中所有節點至少包含一個出邊(懸掛點被看作包含|Vt|個出邊)，發生變化邊的起點至少增加或刪除了一條邊.因此對于任意變化的邊eu,v的起點u，有：

|S(u)t-1∪S(u)t|≥2，

(18)

因此，可進一步推導出：

(19)

(20)

令E[VT]表示節點訪問次數的均值.節點訪問次數與節點總數的乘積為總的訪問次數，總的訪問次數等于隨機游走路徑總長度，故E[VT]=RE[X].由于隨機游走路徑長度服從參數為c的幾何分布，故E[X]=1c，E[VT]=Rc.因此有:

TotalComp≤Rmc+Rnc2.

(21)

當圖G發生變化的增量包含m個節點和n條邊時，IncPR算法根據圖G的中間數據更新結果的時間復雜度為O((cm+n)Rc2).

5　性能測試與分析

5.1實驗設置

本文分別以Bahmani提出的增量PageRank算法[19]和BasicPR作為比較基準，對IncPR的結果正確性和計算量大小進行了實驗.實驗在基于BSP計算模型的Hama分布式計算框架[27]上實現了IncPR和上述2種對比算法.Hama的體系結構如圖5所示.實驗使用的Hama集群由6臺同構節點組成，每個節點配備intel-i7 2600CPU、8GB內存、2TB磁盤，并通過千兆以太網連接.各節點安裝Ubuntu14.04操作系統，主要的計算工具版本分別為Hama-0.6.4、zookeeper-3.4.6和Hadoop-1.2.1.

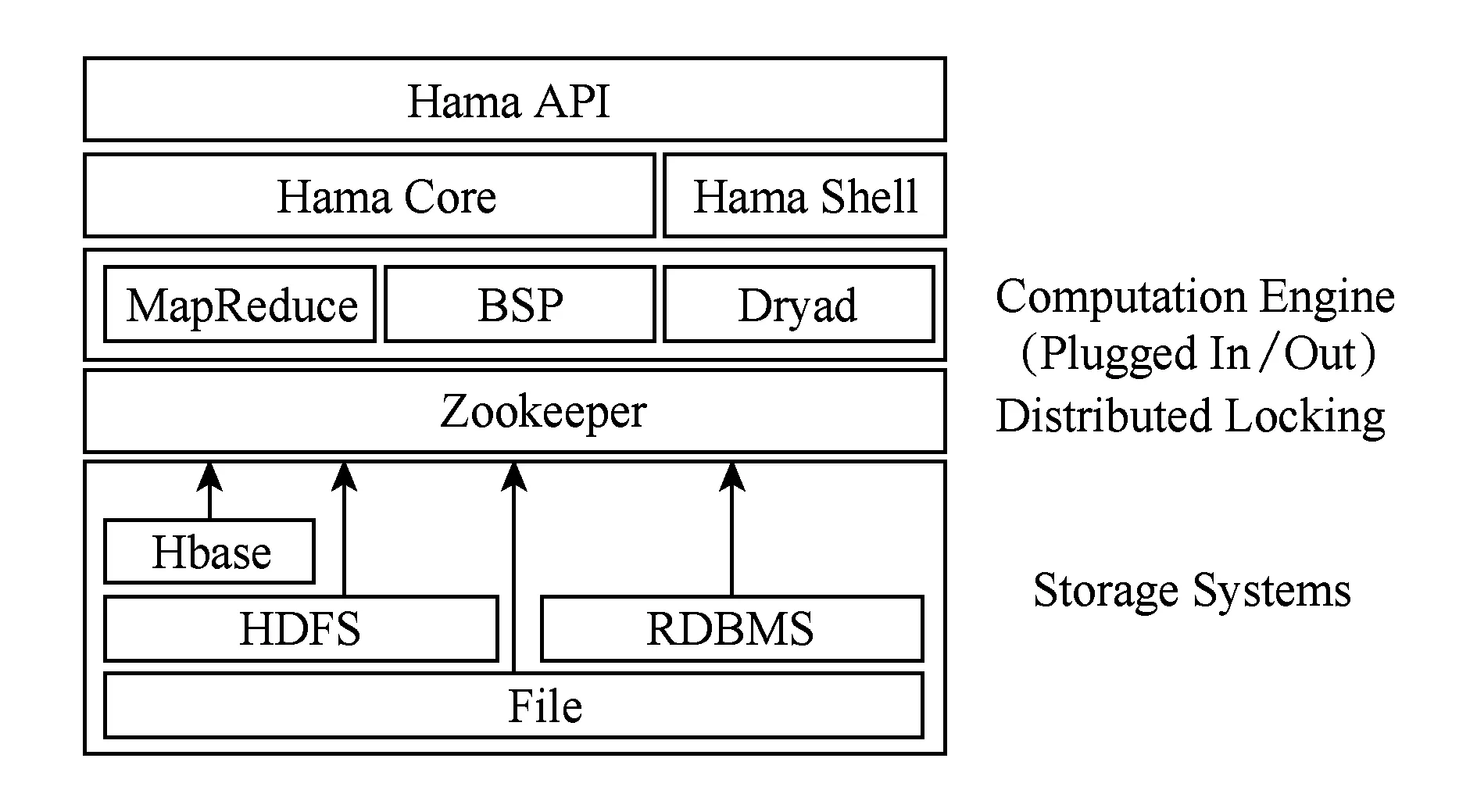
Fig. 5　Overview architecture of Hama.圖5　Hama 分布式計算框架體系結構

實驗使用了多組具有不同應用背景的真實數據集，對典型的數據集變化情況分別進行了多組實驗，實驗結果驗證了IncPR的正確性和計算效率.權衡PageRank結果的精度和實驗運行時間，實驗選取參數R=20，c=0.15，默認情況下，初始的PageRank結果由該參數下的BasicPR計算得到.

5.2評價指標

實驗主要從算法的結果精度和計算量2個方面考慮，選取了2個評價指標，以測試分析IncPR的正確性和計算效率.

1) 正確性指標

類似于已有的相關研究工作[10,14]，本文定義算法正確性的評價指標Err(Alg)如式(22).其中PR(u)代表由算法Alg得到的PageRank的計算結果，π(u)代表PageRank的真實值.顯然地，Err(Alg)的大小代表了算法Alg的結果的相對精度.對于相同的圖數據，Err(Alg)越小意味著算法得到的PageRank的計算結果的精度越高，即越接近真實的PageRank值.本文實驗中PageRank的真實值由PowerIteration算法計算獲得，參數ε=0.000 5.

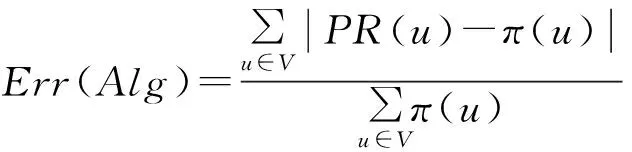
(22)

2) 計算量指標

本文定義Cost(Alg)作為算法計算效率的評價指標.基于蒙特卡羅的PageRank算法通過進行大量的隨機游走來計算PageRank值，構造隨機游走路徑是此類算法的主要開銷.由于隨機游走中每一步的開銷相同，算法的計算量可以由產生的隨機游走的總步數表示.本文實驗基于Hama框架實現，Page-Rank算法通過傳遞消息實現隨機游走，通過統計消息通信的總數即得到隨機游走的總步數.Cost(Alg)的值即等于算法在Hama框架上的發送的消息的總數.

5.3數據集及預處理

實驗使用了多組不同的真實圖數據集[28]，它們覆蓋了從P2P網絡到Web互聯網和社交網絡等多個不同應用領域.數據集的主要特征參數詳見表1所示.類似于文獻[10]中的做法，在不影響實驗結果的準確性和算法計算量的前提下，實驗對圖數據進行了一定的預處理，將圖中所有的單向邊都改為雙向邊.

圖數據的變化包括點和邊的添加和刪除共4種情況.由于增量算法在處理增加刪除邊的2種操作類似(區別僅是在進行隨機游走時經過節點的操作)，因此實驗僅測試添加點和邊情況下算法的正確性和計算效率.僅增加邊的實驗中，先從原圖中隨機選擇最多10%的邊刪除，將得到的圖作為初始數據G，再從被刪除邊中，按固定比例(0.01%，0.05%，0.1%，0.5%，1%，5%，10%)隨機添加到圖G中作為變化后的圖數據.增加點的實驗，以原圖為初始數據G，以G中的節點數為基準，生成固定比例(0.01%，0.05%，0.1%，0.5%，1%，5%，10%)的新節點并添加到G中，隨機地為新節點選擇一條入邊和出邊.

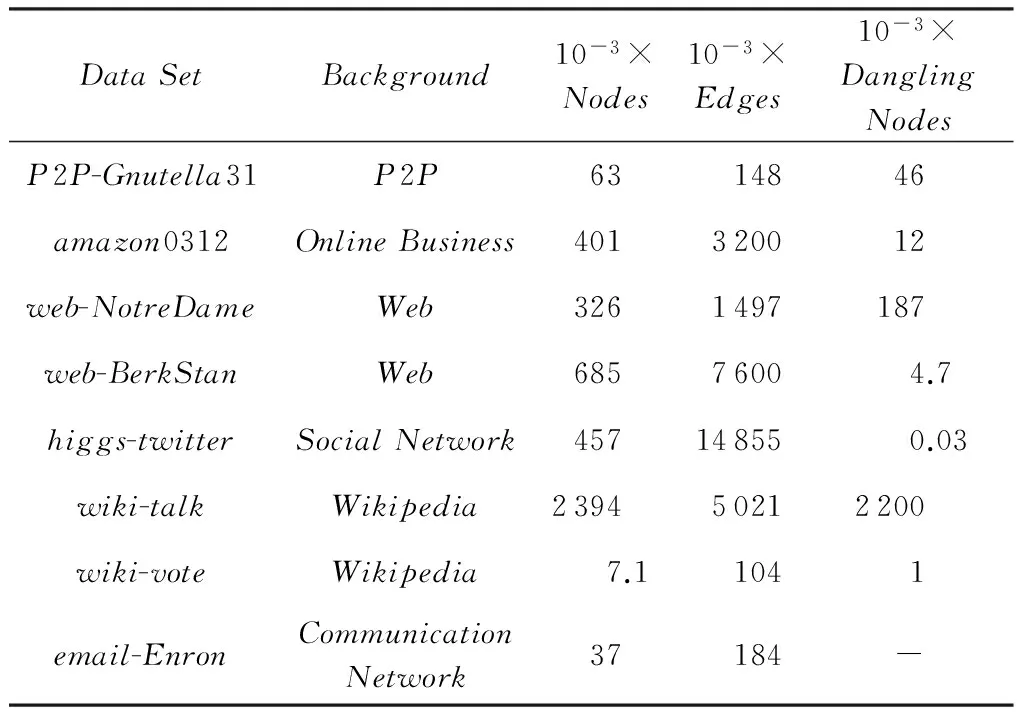
Table 1　Main Parameters of Data Sets表1　數據集的主要特征參數

5.4結果準確性

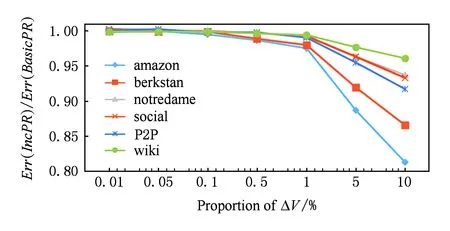
Fig. 6　Comparison of Err(Alg) with different proportion of ΔV.圖6　增加不同比例的節點的誤差比較

本節通過比較IncPR與Bahmani的增量算法和IncPR與BasicPR計算PageRank值的相對誤差的大小，來驗證IncPR的正確性.在比較IncPR與Bahmani的增量算法的正確性時，分別增加不同數量的邊比較2種算法的誤差，實驗表明2種算法具有相同量級的精度水平.在比較IncPR與BasicPR的正確性時，考慮在真實的數據集上，僅增加邊和增加點和邊2種情況下算法的正確性.此外，通過多組不同的實驗，驗證了不同的圖數據變化量、不同的初始結果精度對IncPR結果精度的影響.

如圖6所示，IncPR在結果精度上表現良好.當增量規模較小時(小于1%)，IncPR和BasicPR的結果的誤差接近，隨著增加節點的比例的增大，IncPR與BasicPR的誤差的比在逐漸減小，這意味著IncPR在增加的點較多的情況下(5%和10%)得到比BasicPR更高的結果精度.最優情況下，IncPR的誤差比BasicPR減小接近20%.

圖7反映了增加不同比例的邊(占原圖的0.01%到10%)的情況下，IncPR與BasicPR得到的結果誤差的比值.邊增加的情況下2種算法的誤差總體接近，僅有個別圖得到了最好情況下接近10%的精度提升.另一組增加不同數量的邊的實驗結果(如圖8所示)，也同樣驗證了IncPR得到與BasicPR的結果精度在相同量級的結論.

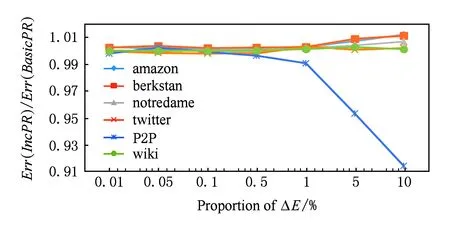
Fig. 7　Comparison of Err(Alg) with different proportion of ΔE.圖7　增加不同比例的邊的誤差比較

Fig. 8　Comparison of Err(Alg) with different number of ΔE.圖8　增加不同數量的邊的誤差比較

對于IncPR比BasicPR獲得的精度提升，一種合理的解釋是圖的變化一定程度地影響了其拓撲結構，BasicPR的結果精度受圖的變化的影響而略有上升，而IncPR采用增量的更新方法，避免了由圖的變化而引入更大的誤差，從而得到了更好的結果精度.圖9所反映的隨著節點的增加BasicPR的誤差上升，一定程度支持了這種解釋.

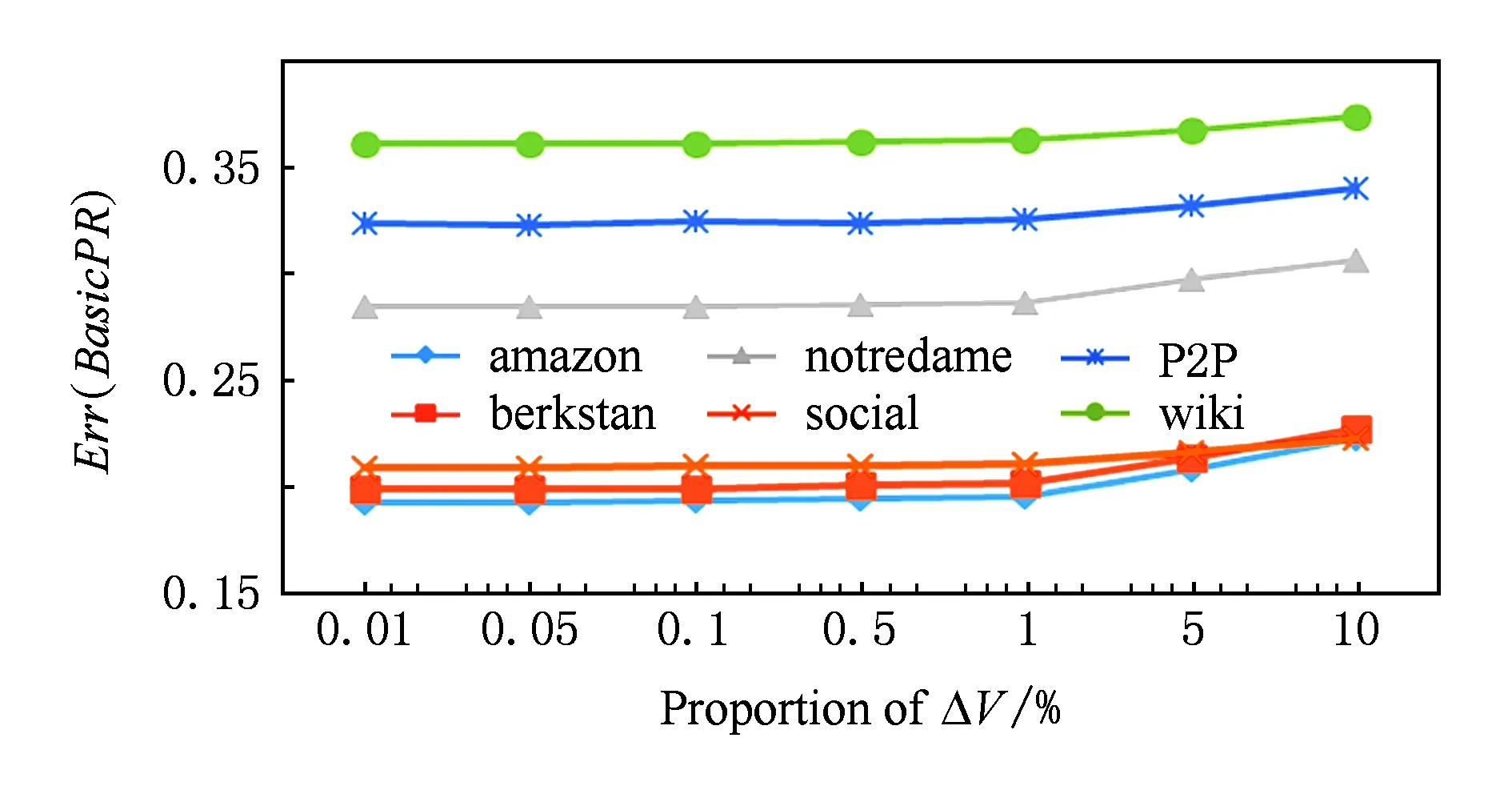
Fig. 9　Err(BasicPR) with different proportion of ΔV.圖9　增加不同比例的節點的BasicPR的結果誤差

此外，IncPR的一個有價值的特點是，其可以通過重用誤差較小的數據獲得精度較高的計算結果.這意味著如果以較大的計算代價計算出高精度的PageRank結果，再使用IncPR處理變化后的新圖，就可以利用較低的成本獲得新的高精度結果，相當于將蒙特卡羅方法適于處理增量和適于并行化的特點與其他的計算代價大但結果精度高的PageRank算法結合了起來，可以充分發揮二者各自的優勢.

圖10和圖11反映了當以PI計算得到的PageRank向量作為初始結果時，增加固定比例的節點和邊的情況下分別得到的IncPR的結果誤差與BasicPR的誤差的比.顯然地，當圖的變化量較小時(不超過1%)，IncPR得到的結果精度顯著優于BasicPR，IncPR得到的結果精度接近PI算法，當增量較大時(5%，10%)，最差情況IncPR的誤差也不到BasicPR的一半.

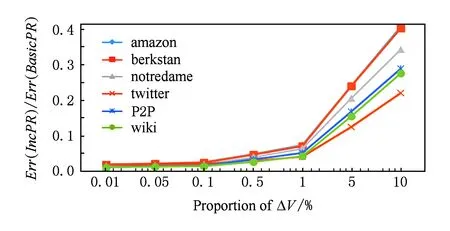
Fig. 10　Comparison of Err(Alg) with different proportion of ΔV (IncPR Starts from PI).圖10　增加不同比例的節點誤差比較(以PI結果作為初始值)

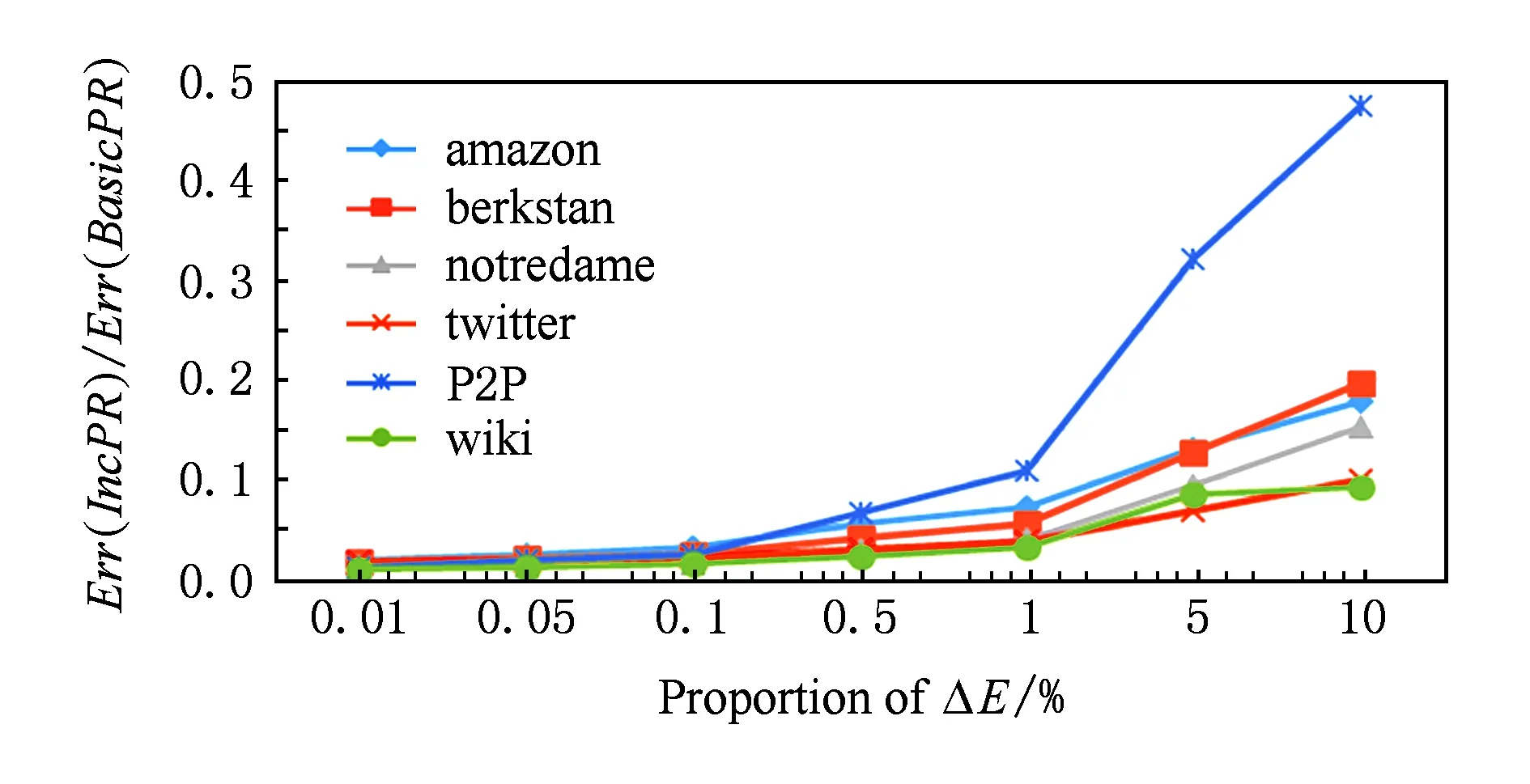
Fig. 11　Comparison of Err(Alg) with different proportion of ΔE (IncPR Starts from PI).圖11　增加不同比例的邊的誤差比較(以PI結果作為初始值)

由于篇幅所限，本文沒有給出IncPR與Bahmani的增量算法的正確性比較的數據，2種算法的結果誤差值相近.

5.5計算量對比

本文通過多組真實數據集上不同場景的實驗，分別比較了IncPR與Bahmani的增量算法及IncPR與BasicPR的計算量的大小，作為評價算法計算效率的標準.

首先對IncPR與Bahmani的增量算法的計算量進行了對比實驗，實驗結果如表2所示.實驗中令增加的邊數n分別為50,100和150，由于Bahmani的增量算法每增加一條邊就更新結果，因此，實驗中統計執行n次Bahmani的增量算法累積的計算量.實驗結果均表明IncPR的計算量明顯優于Bahmani的增量算法，實驗結果驗證了IncPR的時間復雜度優于Bahmani的增量算法.雖然與Bahmani的增量算法的對比實驗中使用的n較小，但由理論分析可知，IncPR的計算量與n的大小呈線性關系，而Bahmani的增量算法的計算量與節點總數|V|的lnn倍呈線性關系，網絡數據中增量的比例占原數據比例較小，n?|V|.因此在n較大的情況下應該會得到類似的結果.

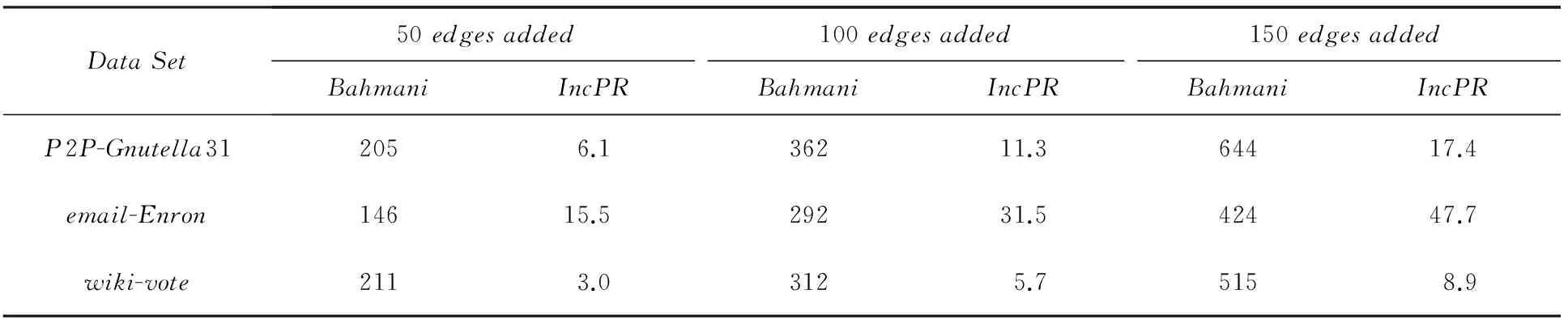
Table 2　Performance Comparison of Bahmani’s and IncPR表2　Bahmani增量算法與IncPR計算量比較　K

進而，本文分別在不同的數據變化量、初始結果精度等多種條件下進行實驗，比較IncPR與BasicPR計算PageRank值的計算量大小，得到算法計算量的統計，作為評價算法計算效率的標準.

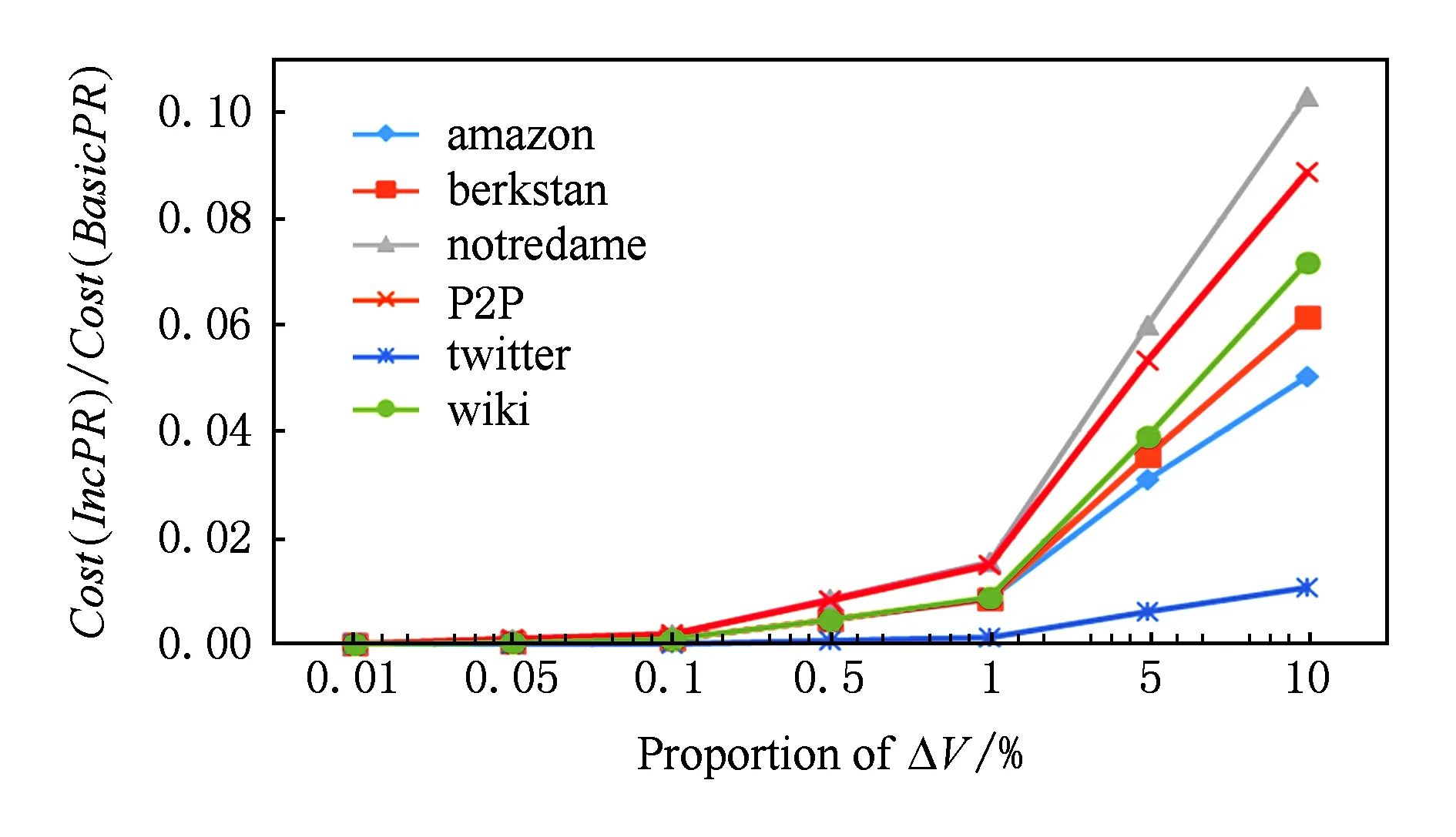
Fig. 12　Comparison of Cost(Alg) with different proportion of ΔV.圖12　增加不同比例節點的計算量比較

圖12與圖13分別反映了增加固定比例的節點和邊的情況下，IncPR與BasicPR的計算量的比值.2組實驗數據都表現出相同的規律，IncPR的計算量明顯小于BasicPR.當圖的變化量不超過0.01%時，IncPR的計算量最大僅為BasicPR的0.09%，當圖的變化量達到10%時，IncPR的計算量最大僅相當于BasicPR的20%.實驗結果表明IncPR能有效地降低PageRank計算的計算量，提高計算效率.

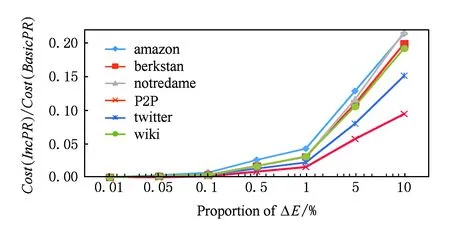
Fig. 13　Comparison of Cost(Alg) with different proportion of ΔE.圖13　增加不同比例邊的計算量比較

圖14反映了增加固定數量的邊的情況下，IncPR的計算量的變化趨勢，不同數據集上的多組實驗反映出相似的規律，即計算量和邊的變化量基本符合線性正比例關系，與理論分析得到的算法的時間復雜度大致相符.

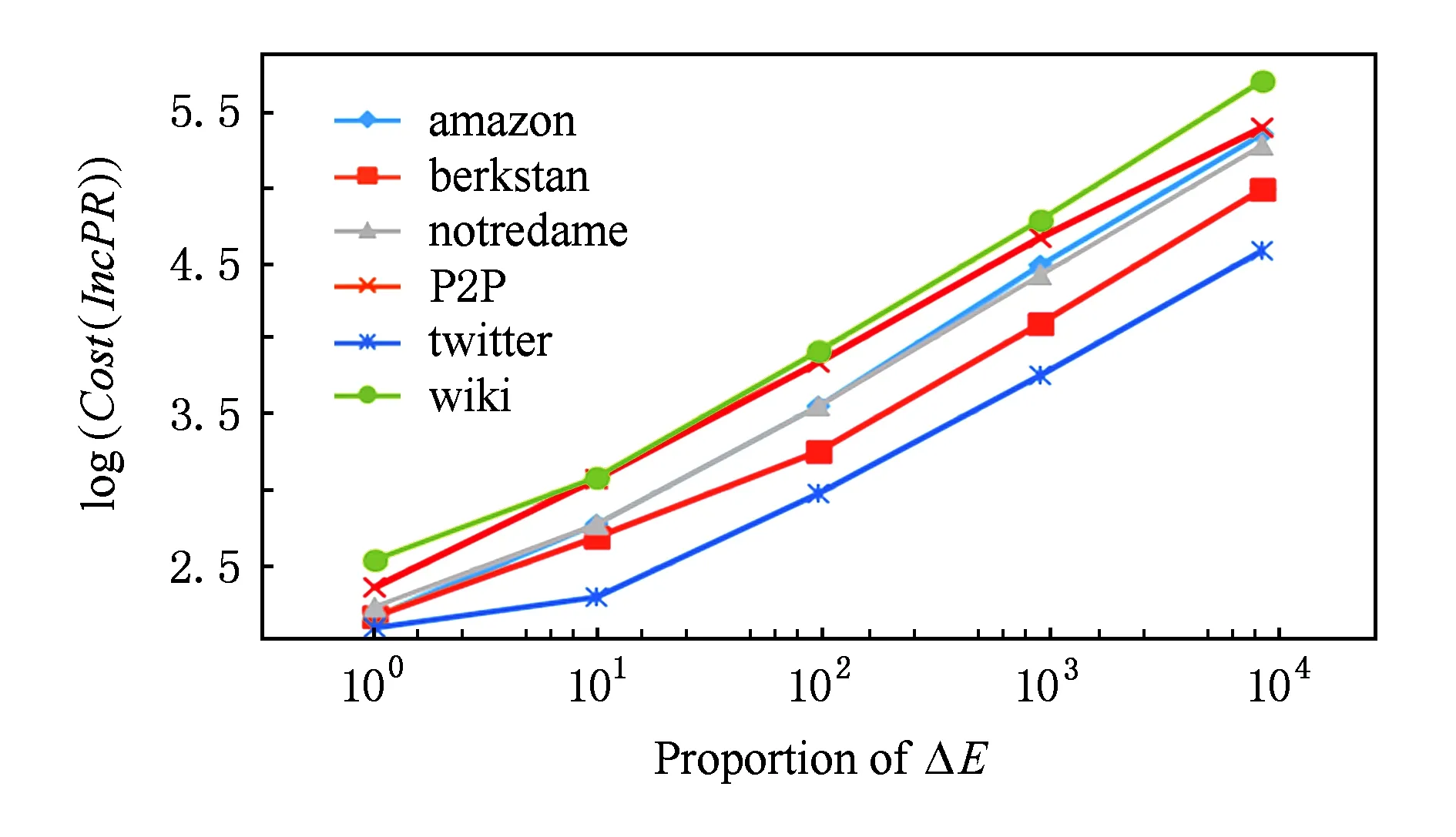
Fig. 14　Relationship of Cost(IncPR) and the number of ΔE.圖14　增加邊的數量與增量算法計算量的關系

6　總　　結

旨在降低頻繁變化的海量數據集上反復計算PageRank帶來的資源消耗，本文提出了一種基于增量計算思想的并行PageRank算法——IncPR.IncPR在時間復雜度上優于已有的相關算法，且不引入額外的存儲開銷.理論分析及基于真實圖數據的大量分布式計算實驗均驗證了IncPR的正確性和計算效率，在保證結果精度的前提下，較之于已有的增量PageRank算法和非增量的PageRank算法，IncPR能夠顯著地降低計算量.此外，IncPR的設計思想也可以用于改進基于蒙特卡羅模擬技術的其他算法(如個性化PageRank、單源最短路徑算法等)，這也將有利于降低此類應用問題的計算成本.

[1]ChinaComputerFederationExpertCommitteeofBigData.WhitePaperonBigDataandIndustryDevelopmentofChina2013[M//OL].Beijing:ChinaComputerFederation, 2013.[2016-03-20].http://www.ccf.org.cn//sites//ccf//ccfziliao.jsp?contentId=2774793649105 (inChinese)

(中國計算機學會大數據專家委員會. 中國大數據與產業發展白皮書2013[M//OL]. 北京: 中國計算機學會, 2013. [2016-03-20].http://www.ccf.org.cn//sites//ccf//ccfziliao.jsp?contentId=2774793649105)

[2]GoogleInc.Googleinsidesearch-google[EB//OL].[2016-03-20].https://www.google.com//intl//ta//insidesearch//howsearchworks//thestory//index.html

[3]KunderM.ThesizeoftheworldwideWeb:EstimatedsizeofGoogle’sindex[EB//OL].[2016-03-20].http://www.worldwidewebsize.com//

[4]WorldWideWebFoundation.Internetlivestats[EB//OL].[2016-03-20].http://www.internetlivestats.com//

[5]PageL,BrinS,MotwaniR,etal.ThePageRankcitationranking:BringingordertotheWeb, 422[R].Stanford,CA:StanfordInfoLab, 1999

[6]DeanJ,GhemawatS.MapReduce:Simplifieddataprocessingonlargeclusters[J].CommunicationsoftheACM, 2008, 51(1): 107-113

[7]ZahariaM,ChowdhuryM,FranklinMJ,etal.Spark:Clustercomputingwithworkingsets[C] //Procofthe2ndUSENIXWorkshoponHotTopicsinCloudComputing(HotCloud).Berkeley,CA:USENIXAssociation, 2010: 10-10

[8]MalewiczG,AusternMH,BikAJC,etal.Pregel:Asystemforlarge-scalegraphprocessing[C] //Procofthe2010ACMSIGMODIntConfonManagementofData.NewYork:ACM, 2010: 135-146

[9]GleichD,ZhukovL,BerkhinP.FastparallelPageRank:Alinearsystemapproach, 38[R].Berkeley,CA:Yahoo!Research, 2004

[10]BahmaniB,ChakrabartiK,XinD.Fastpersonalizedpagerankonmapreduce[C] //Procofthe2011ACMSIGMODIntConfonManagementofData.NewYork:ACM, 2011: 973-984

[11]SarmaAD,MollaAR,PanduranganG,etal.Fastdistributedpagerankcomputation[J].TheoreticalComputerScience, 2015, 561 (PartB): 113-121

[12]AvrachenkovK,LitvakN,NemirovskyD,etal.MonteCarlomethodsinPageRankcomputation:Whenoneiterationissufficient[J].SIAMJournalonNumericalAnalysis, 2007, 45(2): 890-904

[13]ApacheSoftwareFoundation.ApacheHama[EB//OL].[2016-03-20].https://hama.apache.org//

[14]OhsakaN,MaeharaT,KawarabayashiK.EfficientPageRanktrackinginevolvingnetworks[C] //Procofthe21stACMSIGKDDIntConfonKnowledgeDiscoveryandDataMining.NewYork:ACM, 2015: 875-884

[15]LangvilleAN,MeyerCD.Deeperinsidepagerank[J].InternetMathematics, 2004, 1(3): 335-380

[16]SarmaAD,GollapudiS,PanigrahyR.EstimatingPageRankongraphstreams[J].JournaloftheACM, 2011, 58(3): 1165-1182

[17]SarlósT,BenczúrAA,CsalogányK,etal.ToRandomizeornottorandomize:Spaceoptimalsummariesforhyperlinkanalysis[C] //Procofthe15thIntConfonWorldWideWeb.NewYork:ACM, 2006: 297-306

[18]BahmaniB,ChowdhuryA,GoelA.Fastincrementalandpersonalizedpagerank[J].ProceedingsoftheVLDBEndowment, 2010, 4(3): 173-184

[19]KamvarSD,HaveliwalaTH,ManningCD,etal.ExtrapolationmethodsforacceleratingPageRankcomputations[C] //Procofthe12thIntConfonWorldWideWeb.NewYork:ACM, 2003: 261-270

[20]KamvarS,HaveliwalaT,ManningC,etal.ExploitingtheblockstructureoftheWebforcomputingpagerank, 579[R].Stanford,CA:StanfordInfoLab, 2003

[21]LangvilleA,MeyerC.UpdatingPageRankusingthegroupinverseandstochasticcomplementation,CRSC-TR02-32[R].Raleigh:MathematicsDepartment,NorthCarolinaStateUniversity, 2002

[22]LangvilleAN,MeyerCD.Updatingpagerankwithiterativeaggregation[C] //Procofthe13thIntWorldWideWebConfonAlternateTrackPapers&Posters.NewYork:ACM, 2004: 392-393

[23]DesikanP,PathakN,SrivastavaJ,etal.IncrementalPageRankcomputationonevolvinggraphs[C] //SpecialInterestTracksandPostersofthe14thIntConfonWorldWideWeb.NewYork:ACM, 2005: 1094-1095

[24]LofgrenP.OnthecomplexityoftheMonteCarlomethodforincrementalPageRank[J].InformationProcessingLetters, 2014, 114(3): 104-106

[25]TongH,PapadimitriouS,PhilipSY,etal.Proximitytrackingontime-evolvingbipartitegraphs[C] //Procofthe8thSIAMIntConfonDataMining.Philadelphia:SocietyforIndustrialandAppliedMathematicsPublications, 2008: 704-715

[26]McsherryF.AuniformapproachtoacceleratedPageRankcomputation[C] //Procofthe14thIntConfonWorldWideWeb.NewYork:ACM, 2005: 575-582

[27]SeoS,YoonEJ,KimJ,etal.Hama:Anefficientmatrixcomputationwiththemapreduceframework[C] //Procofthe2ndIEEEIntConfonCloudComputingTechnologyandScience,CloudCom.Piscataway,NJ:IEEE, 2010: 721-726

[28]JureLeskovec.Stanfordlargenetworkdatasetcollection[EB//OL].[2016-03-20].http://snap.stanford.edu//data//index.html

JiangShuangshuang,bornin1990.Master.Hermainresearchinterestsincludedistributedcomputing,incrementalcomputinganddatamining.

LiaoQun,bornin1987.PhDcandidate.Hismainresearchinterestsincludedistributedcomputing,taskschedulinganddatamining.

YangYulu,bornin1961.ProfessorandPhDsupervisorinNankaiUniversity.Hismainresearchinterestsincludeinterconnectionnetwork,parallelanddistributedprocessing.

LiTao,bornin1977.PhDandassociateprofessorinNankaiUniversity.MemberoftheACMandtheIEEEComputerSociety,SeniormemberofChinaComputerFederation.Hismainresearchinterestsincludeparallelanddistributedprocessing,high-performancecomputingandnetworkinformationmining.

IncPR:AnIncrementalParallelPageRankAlgorithm

JiangShuangshuang,LiaoQun,YangYulu,andLiTao

(College of Computer and Control Engineering, Nankai University, Tianjin 300350)

PageRankalgorithmplaysanimportantroleinvariousareassuchasinformationretrievalandsocialnetworkanalysis.ThecontinuouslyincreasingsizeofnetworksandthetimelinessrequirementsmakeitbringenormouscomputationaloverheadtorepeatcalculatingPageRankforamassiveandevolvingnetwork.Therefore,IncPR,aPageRankalgorithmbasedontheideaofincrementalcomputationmodelisproposed.IncPRreusesexistingresultsfrompreviouscomputationandmodifiesPageRankvaluesaccordingtothechangedpartofdatasetsaccumulativelyviaanextendedMonteCarlomethod,whichcaneffectivelyavoidreduplicatedcomputationandimprovetheperformanceofPageRankcomputingwithnoadditionalstorageoverhead.TheoreticalanalysisshowsthatthecomputationalcomplexityofIncPRprocessinganevolvingnetworkwithmnodesandnedgeschangedisO((cm+n)Rc2),wherecistheresetprobabilityandRisthenumberofrandomwalksstartingfromeachnode.ThecomputationalcomplexityofIncPRislowerthanotherexistingrelatedalgorithms.Ourevaluationswithtypicalreal-worldgraphsuponaHamaclusteralsodemonstratethatIncPRobtainsPageRankvalueswithequal(orevenhigher)accuracyasthebaselineMonteCarloPageRankalgorithmandreducestheamountofcomputationsignificantly.Inexperimentswith0.01%datachanged,IncPRreducesover99.9%amountofcomputation.

PageRank;Webmining;incrementalcomputing;MonteCarloalgorithm;parallelanddistributedprocessing

2016-03-21；

2016-05-25

TP391