十五相感應電機對稱缺相運行時的定子漏抗計算

鄭曉欽　王　東

(1.華中科技大學電氣與電子工程學院　武漢　430074 2.艦船綜合電力技術國防科技重點實驗室(海軍工程大學)　武漢　430033)

?

十五相感應電機對稱缺相運行時的定子漏抗計算

鄭曉欽1王東2

(1.華中科技大學電氣與電子工程學院武漢430074 2.艦船綜合電力技術國防科技重點實驗室(海軍工程大學)武漢430033)

定子參數計算是應用等值電路進行多相感應電機對稱缺相運行性能分析的基礎。通過引入關聯矩陣反映所缺相數，分別對定子槽漏抗、諧波漏抗、端部漏抗進行計算，得到了十五相感應電機缺一個五相、兩個五相繞組對稱工況下的定子漏抗。計算結果表明，對于整距集中繞組的十五相感應電機，缺少五相或十相后，每相槽漏抗不變，諧波漏抗增大，而端部漏抗減小，故對稱缺相運行工況下的定子漏抗參數與正常工況下并無明確倍數關系。在正常工況及缺十相對稱運行工況下對十五相感應電機原理樣機進行了堵轉試驗，試驗測得的短路電抗與計算值相互吻合，間接驗證了計算結果的正確性。

十五相感應電機對稱缺相運行等值電路定子漏抗

0　引言

近年來，隨著船舶電力推進等大功率驅動應用領域的快速發展，多相感應推進電機及其調速系統成為研究熱點[1- 4]。相比傳統三相電機，多相推進電機具有諧波含量低、轉矩性能平穩、可靠性高等諸多優勢[5-7]。特別對于十五相推進感應電機，出現定子繞組一相或多相開路故障時，可直接切除含故障相的整個五相甚至十相繞組繼續降額運行。但因十五相推進感應電機應用背景特殊，鮮有其對稱缺相運行性能分析的報道[8，9]。考慮到定子參數計算是應用等值電路進行性能分析的基礎，尤其缺相后的漏抗參數發生了變化，其計算的準確性直接影響電機對稱缺相穩態運行與暫態運行性能的分析。

定子漏抗參數包括槽漏抗、諧波漏抗與端部漏抗三部分，文獻[10-13]給出了三相電機定子漏抗的計算公式，但這些公式大都不能直接用于多相電機定子漏抗的計算。對于多相電機定子槽漏抗、諧波漏抗與端部漏抗的計算方法，文獻[14-20]已經作了較為詳細的說明，但都只在對稱正常工況下進行計算，均未考慮缺相工況下的漏抗參數計算，也未見有對稱缺相運行時定子漏抗參數變化規律的總結。鑒于現有方法在計算不同相數定子漏抗參數時，需根據相數的改變重新列寫公式求解，且不同繞組結構下的計算公式也不同，應用到多相電機對稱缺相運行參數計算時十分麻煩，故有必要提出一套適用于任意缺相工況下定子漏抗計算的通用方法。

本文從網絡圖論的基本原理出發，引入反映相繞組與各槽線圈邊間及相繞組與各槽線圈間連接關系的關聯矩陣，通過關聯矩陣中相應元素的變化體現所缺相數，計算了一臺45 kW十五相感應電機原理樣機在不同對稱缺相運行工況下的槽漏抗、諧波漏抗和端部漏抗。所用計算方法通用性強，方便規范統一編程，適用于任意繞組結構的多相感應電機缺相工況下定子漏抗參數計算。

1　十五相感應電機繞組結構

該十五相推進感應電機(電機基本數據參見附錄)定子繞組由3個五相繞組組成，每個五相繞組各相互差2π/5電角度，每兩個五相繞組間互移π/15電角度，十五相繞組的中點相互獨立，構成中點獨立的半對稱繞組。若十五相中任一相發生開路故障，則可將含故障相的整個故障五相繞組全部切除，剩余十相繞組對稱運行；若任意兩個五相中同時出現多相繞組開路故障，則可將含故障相的整個十相全部切除降額運行，電機缺相前后繞組分布變化如圖1所示。

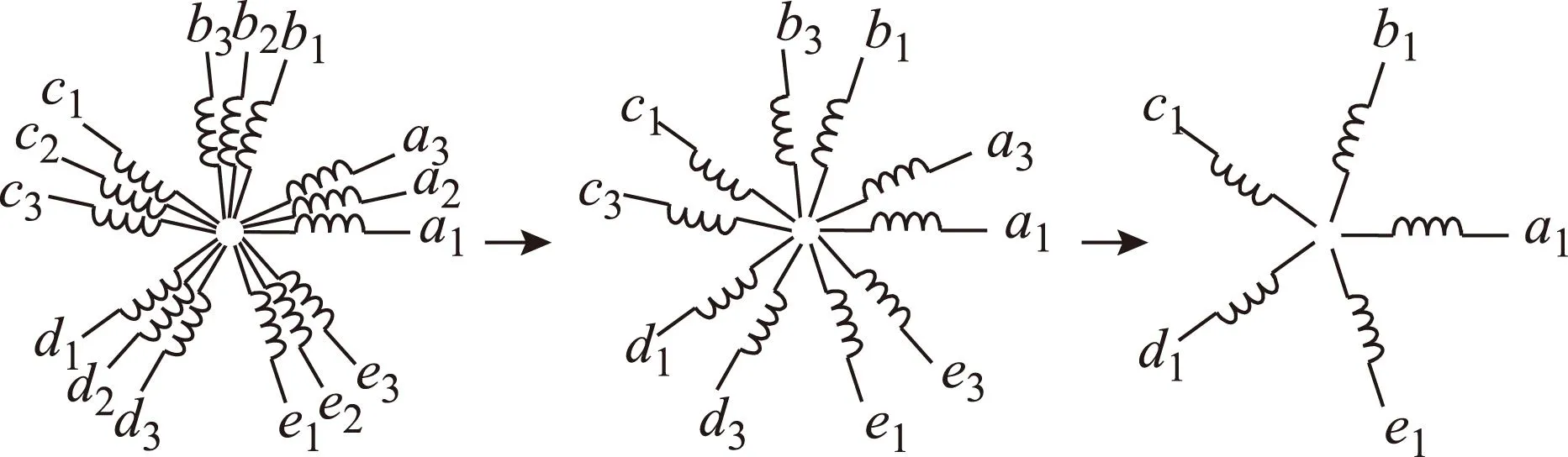
圖1　十五相電機對稱缺相運行定子繞組變化Fig.1　Stator windings change of 15-phase inductance motor under symmetrical fault condition

對于缺相后的感應電機，定子繞組分布仍然對稱，但各參數均已發生了變化。因此，在進行電機對稱缺相運行性能分析時必須考慮缺相引起的定子漏抗變化。下面具體介紹定子各部分漏抗缺相后的計算方法及變化規律。

2　定子槽漏抗計算

該十五相感應電機定子采用半開口矩形槽，故槽比漏磁導計算較為簡單。圖2給出了定子槽型，可分為兩部分，即槽口與槽楔部分和槽身部分。

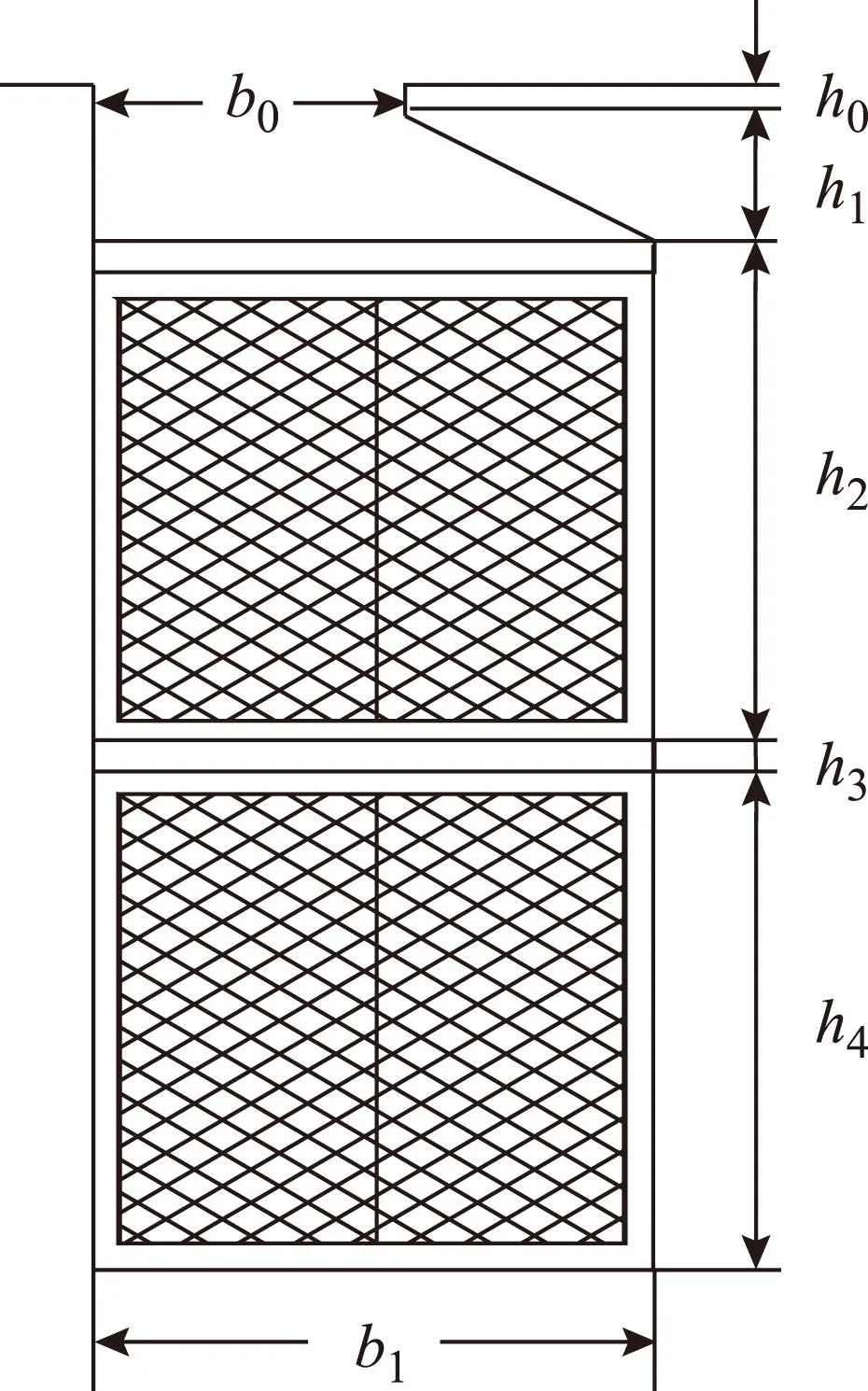
圖2　定子半開口槽Fig.2　Stator semi-opening slot

計算過程中所做假設條件為：①電流在導體截面上均勻分布；②忽略鐵心磁阻不計，槽漏磁動勢全部消耗在槽中；③定子槽中所有磁力線與電樞表面平行。

設上、下層線圈邊中串聯導體數均為W，則上層線圈邊的自感Ms11、下層線圈邊的自感Ms22、上下層線圈邊的互感Ms12分別為

(1)

式中，λ11為相應于上層線圈邊自感的槽自比漏磁導；λ22為相應于下層線圈邊自感的槽自比漏磁導；λ12為相應于上下層線圈邊互感的槽互比漏磁導，其值可根據文獻[7]直接寫出

(2)

在由式(1)、式(2)計算各相槽漏感時，為能將缺相工況與正常工況下的相間繞組關系進行統一表示，清楚地反映15相感應電機定子繞組15個槽自漏感與相間210個槽互漏感(只計算105個即可)在缺相前后的關系，引入相繞組與各槽線圈邊間的關聯矩陣B。仿照電路網絡中列寫回路與支路關聯矩陣的方法，將每槽線圈邊當成一條支路，每相繞組當成一個回路。當各相繞組回路電流方向與每槽線圈邊支路電流方向一致時，B中對應元素為1，二者方向相反時對應元素為-1，無關聯時則用0表示。由于原理樣機定子槽數為60，每相繞組均分上下兩層線圈邊，故關聯矩陣B為30×60階。

圖3為a1相繞組一對極下的繞組連接，并規定了線圈邊電流正方向以及繞組回路電流正方向(由x1端流入，a1端流出)。

圖3　線圈邊電流正方向以及繞組回路電流正方向Fig.3　Positive direction of coil edge and winding loop currents

其余各相繞組與a1相連接方式相同，這里不再一一畫出。根據圖中規定的線圈邊電流正方向及各相繞組電流方向，可列寫相繞組與各槽線圈邊間的關聯矩陣B。若按a1相下、上層邊，b1相下、上層邊，c1相下、上層邊，…，直到e3相下、上層邊的順序列寫，并考慮到每相中二對極下的元素相同，則十五相正常工況下的關聯矩陣B可寫為

式中，B1、B2、B3均為10×30階子矩陣，分別對應a1～e1、a2～e2以及a3～e3五相繞組一對極下元素。

例如，B1中第1、2行為對應a1相一對極下的元素，其值為

當發生繞組開路故障后，只需將矩陣中相應開路相的元素變為0即可。因此，電機在十相對稱缺相運行(缺五相)工況下的關聯矩陣B為

五相對稱缺相運行(缺十相)工況下的關聯矩陣B為

可以看出，無論正常工況亦或對稱缺相運行工況，關聯矩陣B均為30×60階矩陣，只是所缺相元素變為0而已，故列寫過程簡單靈活。

設b[(2m-2+i)，k]和b[(2n-2+j)，k]分別為B中第2m-2+i行、第k列和第2n-2+j行、第k列元素，可得第m相與第n相間槽漏感為

(3)

式中，m=1，2，3，…，15；n=1，2，3，…，15；當m=n時，即為每相槽自漏感。

由式(3)得到的各相槽漏感為15×15階矩陣，包括15個槽自漏感及105個槽互漏感。可進一步以a1相為基準對每相槽漏抗進行折算，得到電機對稱運行情況下考慮所有相繞組共同作用時的定子每相槽漏抗為

(4)

式中，Ls[1，5(k-1)+i]為a1相繞組的槽自漏感及與其他各相的相間槽互漏感，H。

根據式(1)～式(4)計算了十五相感應電機正常運行及不同對稱缺相運行時的槽漏抗，見表1。

表1　整距繞組不同缺相工況下槽漏抗Tab.1　Slot leakage reactance of full-pitch stator winding under different symmetrical faultconditions

由于原理樣機定子采用整距集中繞組，同槽中上、下層線圈邊均屬同相繞組，相間槽互漏抗均為0，因此即使在對稱缺相工況下，剩余各相槽漏抗仍保持不變。若定子采用短距繞組，則相間槽互漏抗不再為0，缺相后各相槽漏抗會發生改變。為證明繞組結構對缺相前后各相槽漏抗的影響，利用現有原理樣機結構尺寸，將短距比人為改為13/15，為與整距集中繞組下的關聯矩陣對比，同樣給出了子矩陣B1中對應a1相一對極下的元素。

根據修改后的關聯矩陣重新計算了短距繞組時不同對稱缺相運行工況下的相槽漏抗，結果見表2。

表2　短距繞組不同缺相工況下槽漏抗Tab.2　Slot leakage reactance of short-pitch stator winding under different symmetrical fault conditions

由表2計算結果可看出，十五相電機在十相和五相對稱缺相運行工況下，由于缺相引起相間槽互漏抗的減少，最終導致各相槽漏抗發生變化。因此，定子繞組結構不同，多相電機對稱缺相運行工況下的各相槽漏抗變化情況也不同。而無論何種繞組結構，在何種缺相故障工況下，均可通過關聯矩陣B清晰有效地反映相繞組與各槽線圈邊間的連接關系。

3　定子諧波漏抗計算

為統一計算不同工況下的各相諧波漏抗，先以單一線圈為基礎，通過總電感減去基波電感的方法計算兩線圈間的諧波電感，對于本文原理樣機60個定子槽中的任意兩槽線圈間的諧波漏感可按文獻[16]中的方法計算，本文不再贅述。與相間槽漏抗計算方法相似，這里引入相繞組與各槽線圈間的關聯矩陣C，計算不同對稱缺相運行工況下的各相諧波漏抗。

同樣將每槽線圈當成一條支路，每相繞組當成一個回路，列寫每相繞組在整個2對極下所有線圈的分布情況，即15×60階矩陣。圖4仍以一對極下的a1相繞組為例，給出了線圈電流正方向及相繞組電流方向。

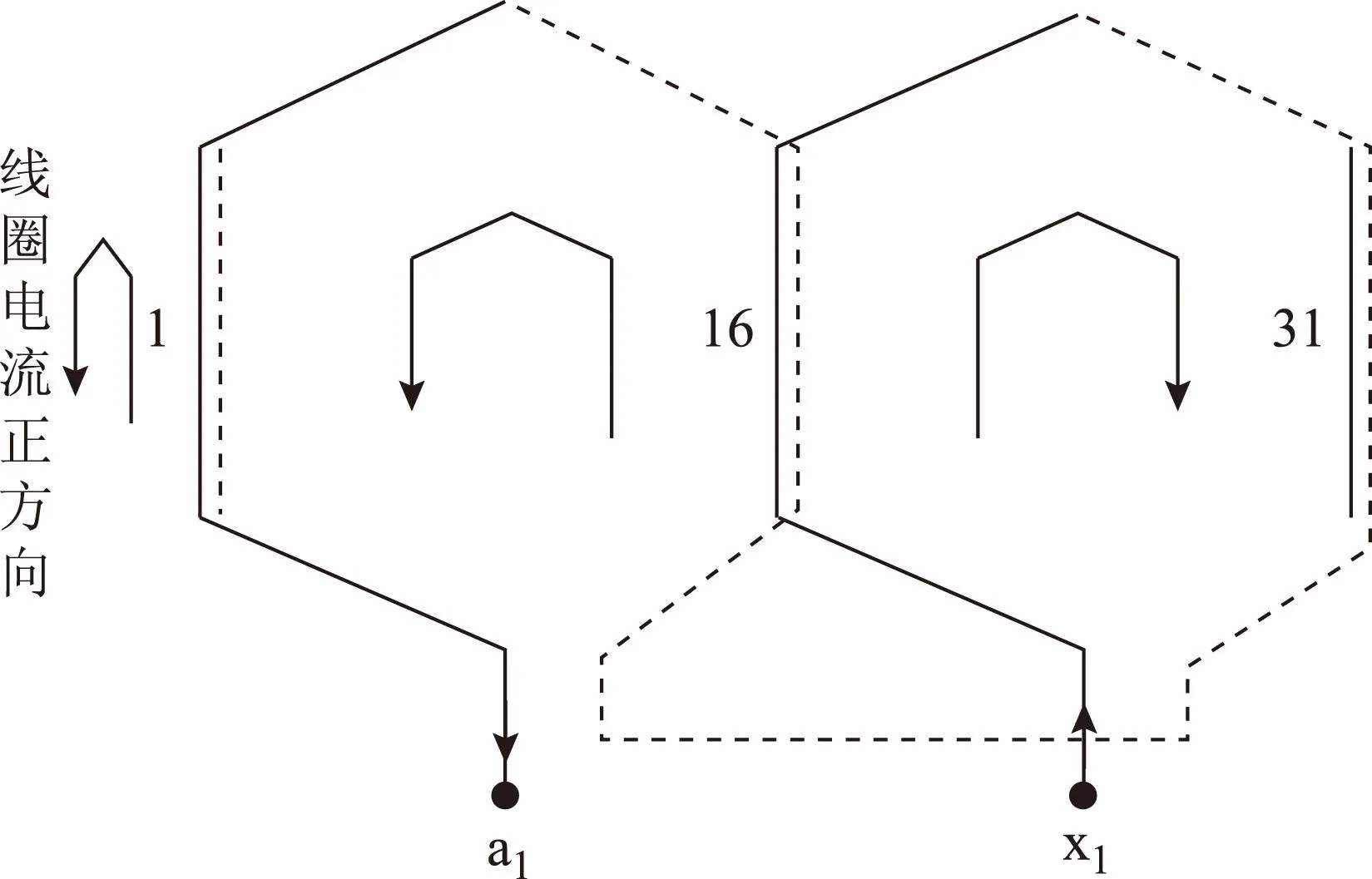
圖4　線圈電流正方向及相繞組電流方向Fig.4　Positive direction of coil and winding loop currents

按a1相、b1相、c1相、…、e3相的排序進行列寫，則十五相正常工況下的關聯矩陣C可寫為

式中，C1、C2、C3均為5×30階子矩陣，分別對應a1～e1、a2～e2以及a3～e3五相繞組一對極下元素。

例如，C1中對應a1相一對極下的元素為

設c(m，i)和c(n，j)分別為C中第m行、第i列和第n行、第j列元素，則第m相與第n相間諧波漏感為

(5)

式中，Mh(i，j)為第i線圈與第j線圈間的諧波電感，H。

同理，在求得15×15階各相諧波漏感矩陣后，以a1相為基準進行折算，則考慮所有相繞組共同作用時的定子每相諧波漏抗為

(6)

根據式(5)、式(6)分別計算了十五相感應電機正常運行及不同對稱缺相運行時的相諧波漏抗，結果如表3所示。

表3　整距繞組不同缺相工況下諧波漏抗Tab.3　Harmonic leakage reactance of full-pitch stator winding under different symmetrical fault conditions

由表3中計算結果可看出，隨缺相數量的增加，各相諧波漏抗逐漸增大。這是由于諧波漏抗為各次諧波磁場所感生的基頻電動勢對應的電抗，其大小與氣隙中諧波磁動勢的多少密切相關。定子相數減少，對稱電流在氣隙中產生的諧波旋轉磁動勢增多，相應的各相諧波漏抗會隨之增大。此外，諧波漏抗大小還與繞組連接方式相關，即當電機相數一定時，整距集中繞組與短距分布繞組的各相諧波漏抗也不相同。其差別體現在第i線圈與第j線圈間的諧波電感Mhij中，而整距繞組與短距繞組的關聯矩陣C均相同。為證明繞組結構對缺相前后各相諧波漏抗的影響，同樣利用現有原理樣機尺寸，計算了短距比為13/15時不同對稱缺相運行工況下的相諧波漏抗，結果見表4。

表4　短距繞組不同缺相工況下諧波漏抗Tab.4　Harmonic leakage reactance of short-pitch stator winding under different symmetrical fault conditions

對比表3、表4計算結果可看出，短距繞組對諧波漏抗有明顯削弱作用，且相數越少削弱作用越明顯。而在15相電機正常工況下，由于本身諧波含量較低，因此短距繞組結構無太明顯優勢。

4　定子端部漏抗計算

本文在計算端部漏感時仍沿用文獻[14，17]中的思路，引入氣隙電流和鏡像電流，以Biot-Savart定律為基礎，將線圈端部各大段分成若干小段，用數值方法計算兩線圈間端部電感。同樣通過相繞組與各槽線圈間的關聯矩陣C可求得第m相與第n相間端部漏感為

(7)

式中，Me(i，j)為第i線圈與第j線圈間的端部電感，H。

與各相槽漏抗和諧波漏抗計算類似，最終折算為所有相繞組共同作用時的定子每相端部漏抗。表5為十五相感應電機正常運行及不同對稱缺相運行時的端部漏抗。

表5　整距繞組不同缺相工況下端部漏抗Tab.5　End-winding leakage reactance of full-pitch stator winding under different symmetrical fault conditions

由表5中計算結果可看出，隨相數的減少，各相端部漏抗明顯減小，但由于受線圈端部所跨機械角度等因素影響[17]，其大小變化與相數間并無明確的反比關系存在，而與繞組的短距比密切相關，故繞組連接方式也會對不同缺相工況下的端部漏抗產生影響。表6為短距比為13/15時不同對稱缺相運行工況下的各相端部漏抗。

表6　短距繞組不同缺相工況下端部漏抗Tab.6　End-winding leakage reactance of short-pitch stator winding under different symmetrical fault conditions

綜合表5、表6中的計算結果，無論是整距集中繞組還是短距分布繞組，缺相后各相端部漏抗均隨相數的減少而減小。

5　計算結果的間接試驗驗證

根據上述計算結果可得到十五相感應電機在不同對稱缺相運行工況下的定子漏抗，由于堵轉試驗所測得漏電抗為定、轉子漏抗之和，無法再將二者進行分離，所以試驗只能間接驗證定子漏抗計算結果。

現對45 kW十五相感應電機原理樣機進行堵轉試驗，分別測量電機十五相運行與五相運行時的短路漏抗，即定、轉子總漏抗。試驗中，電機由十五相變頻器供電，調制方式采用基于載波層疊的PWM脈寬調制，由錄波儀同時采集定子a1～e1、a2共6相電壓、電流數據。對錄波儀采集的各相電壓、電流進行Fourier分解，得到基波電壓U1、基波電流I1及兩者間的相位差，進而可求得各相基波短路漏抗，最終將6相的基波短路漏抗平均值作為電機的基波堵轉漏抗。表7為不同相數工況下短路漏抗的計算值與實測值對比。

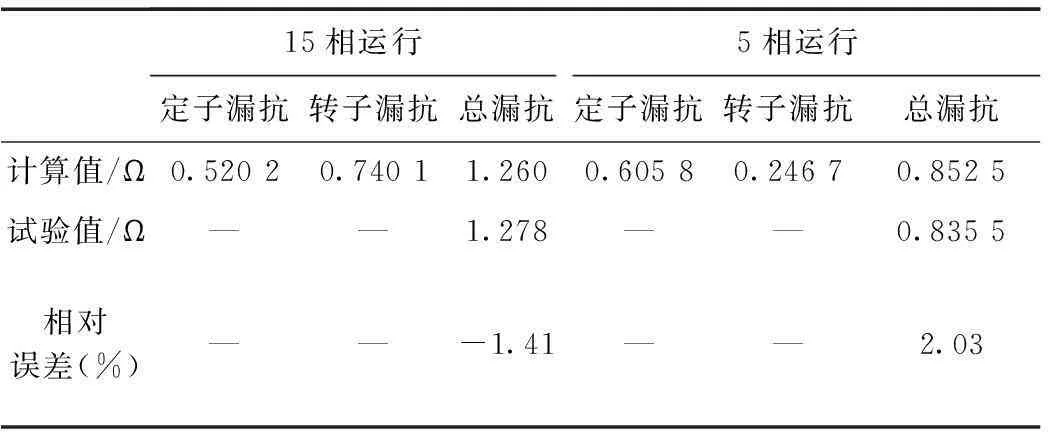
表7　不同缺相工況下短路漏抗結果對比Tab.7　Calculated and measured short-circuit reactances under different conditions

表7中定子漏抗計算值為表1、表3、表5中各相槽漏抗、諧波漏抗與端部漏抗之和。籠型轉子漏抗采用傳統方法[21，22]求得，只是在剩余5相對稱缺相運行時，向定子繞組折算系數變為15相正常工況時的1/3。從表中的對比結果可知，最大誤差僅為2.03%，說明不同工況下的總漏抗計算值較為準確。

6　結論

本文以一臺45 kW十五相感應電機原理樣機為例，通過引入相繞組與各槽線圈邊間的關聯矩陣及相繞組與各槽線圈間的關聯矩陣，分別計算了電機在正常工況下及十相、五相對稱缺相運行工況下的定子各相槽漏抗、諧波漏抗和端部漏抗。計算方法不僅適用于多相電機在對稱缺相運行工況下的定子漏抗計算，同樣適用于不對稱缺相運行工況。只是在不對稱缺相運行工況下，定子各相電流不再對稱，故無需再折算為考慮所有相繞組共同作用時的每相漏抗，只需通過關聯矩陣求得各線圈間的互感矩陣即可。在應用關聯矩陣計算不同工況定子漏抗時無需重新編程，只通過關聯矩陣中相應元素的變化體現相數的變動即可，計算過程簡便清晰，具有較強的通用性。

鑒于整距集中繞組同槽中上、下層線圈邊均屬同相繞組，只存在槽自漏抗，相間槽互漏抗均為0，故各相槽漏抗不隨相數改變而改變。而短距分布繞組同槽中的兩層線圈可能屬于不同相繞組，相間槽互漏抗不再為0，因此各相槽漏抗會隨相數的減少而改變。

由于電機相數與空間旋轉磁動勢次數密切相關，相數越少，多相對稱電流在氣隙中產生的諧波旋轉磁動勢越多，故在對諧波磁動勢無任何削弱作用的整距集中繞組中，各相諧波漏抗會隨缺相數量的增多而大幅增加，而對于短距分布繞組來說，各相諧波漏抗在缺相后的增量要明顯減小。

在各相端部漏抗的計算過程中，由于涉及與繞組短距比相關的線圈端部所跨機械角度等量，因此繞組連接方式也會對不同缺相工況下的端部漏抗產生影響，但總體變化趨勢相同，均隨缺相數量的增多而減小。

綜合各相槽漏抗、諧波漏抗和端部漏抗的變化趨勢，各相定子總漏抗在電機對稱缺相運行時的變化并無規律可循，通過本文中方法可方便的計算不同缺相工況下的定子漏抗。通過對原理樣機的堵轉試驗，測得電機十五相正常工況與五相對稱缺相運行工況下的短路電抗，與計算得出的電機定轉子總漏抗進行對比，兩者誤差較小，從而間接驗證了本文在計算十五相電機對稱缺相運行工況下定子漏抗過程中所用方法的準確性。

附錄

樣機參數：

1)樣機數據：額定功率PN=45 kW；相數m=15；極對數p=2；額定相電壓(基波)UN=140 V；額定相電流(基波)IN=25 A；基波頻率f=20 Hz。定子槽數Z1=60；定子采用雙層整距集中繞組，線圈單層匝數N=12，每相串聯總匝數W=48；并聯支路數A=1。轉子槽數Z2=38；轉子采用直槽籠型轉子。

2)定子槽型尺寸：槽口寬b0=5.4 mm；槽寬b1=9.3 mm；槽口高h0=1 mm；槽楔高h1=3 mm；單層繞組高h2=h4=20 mm；層間絕緣墊條高h3=2.5 mm。

[1]Jones M，Vukosavic S N，Dujic D，et al.A synchronous current control scheme for multiphase induction motor drives[J].IEEE Transactions on Energy Conversion，2009，24(4)：860-868.

[2]Tani A，Mengoni M，Zarri L，et al.Control of multi-phase induction motors with an odd number of phases under open circuit faults[J].IEEE Transactions on Power Electronics，2012，27(2)：565-577.

[3]Apsley J M.Derating of multiphase induction machines due to supply imbalance[J].IEEE Transactions on Industry Applications，2010，46(2)：798-805.

[4]Abdel-Khalik A S，Morsy A，Ahmed S，et al.Effect of stator winding connection on performance of five-phase induction machines[J].IEEE Transactions on Industrial Electronics，2014，61(1)：3-19.

[5]楊家強，高健，金玉龍，等.基于矢量控制的多相感應電機電子變極調速技術[J].電工技術學報，2014，29(3)：96-102.

Yang Jiaqiang，Gao Jian，Jin Yulong，et al.Electronic pole-changing speed adjusting technology of multiphase induction motors based on vector control[J].Transactions of China Electrotechnical Society，2014，29(3)：96-102.

[6]袁飛雄，黃聲華，龍文楓.六相永磁同步電機諧波電流抑制技術[J].電工技術學報，2011，26(9)：31-36.

Yuan Feixiong，Huang Shenghua，Long Wenfeng.Techniques to restrain harmonics of six-phase permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society，2011，26(9)：31-36.

[7]紀鋒，王公寶，付立軍，等.十二相同步發電機降階等效模型研究[J].電力系統保護與控制，2012，40(2)：28-33.

Ji Feng，Wang Gongbao，Fu Lijun，et al.Study on equivalent reduced model of twelve-phase synchronous generator[J].Power System Protection and Control，2012，40(2)：28-33.

[8]陳林.十五相感應電機定子繞組多相開路的穩態特性[J].電工技術學報，2004，19(11)：14-19.

Chin Lin.Steady state performance of a 15-phase induction machine with multiphase stator windings open circuited[J].Transactions of China Electrotechnical Society，2004，19(11)：14-19.

[9]劉自程，鄭澤東，彭凌，等.船舶電力推進中十五相感應電機同軸運行及容錯控制策略[J].電工技術學報，2014，29(3)：65-74.

Liu Zicheng，Zheng Zedong，Peng Ling，et al.Fixed joint double fifteen-phase induction motor control and fault-tolerant control in ship propulsion system[J].Transactions of China Electrotechnical Society，2014，29(3)：65-74.

[10]陳世坤.電機設計[M].2版.北京：機械工業出版社，1990：50-62.

[11]程福秀，林金銘.現代電機設計[M].北京：機械工業出版社，1993：155-156.

[12]Boldea I，Nasar S A.The induction machines design handbook[M].Second Edition.Boca Raton：CRC Press，2010：119-139.

[13]Boglietti A，Cavagnino A，Lazzari M.Computational algorithms for induction-motor equivalent circuit parameter determination—part Ⅰ：resistances and leakage reactances[J].IEEE Transactions on Industrial Electronics，2011，58(9)：3723-3733.

[14]王東，吳新振，馬偉明，等.非正弦供電十五相感應電機定子漏抗計算[J].中國電機工程學報，2010，30(6)：41- 47.

Wang Dong，Wu Xinzhen，Ma Weiming，et al.Calculation of stator leakage reactances of fifteen-phase induction motor with non-sinusoidal supply[J].Proceedings of the CSEE，2010，30(6)：41- 47.

[15]吳新振，王祥珩.12/3相雙繞組異步發電機定子槽漏抗的計算[J].中國電機工程學報，2007，27(12)：46-51.

Wu Xinzhen，Wang Xiangheng.Calculation of stator slot leakage inductance for 12/3-phase dual-winding induction generator[J].Proceedings of the CSEE，2007，27(12)：46-51.

[16]吳新振，王祥珩.12/3相雙繞組異步發電機定子諧波漏抗的計算[J].中國電機工程學報，2007，27(21)：71-75.

Wu Xinzhen，Wang Xiangheng.Calculation of stator harmonic leakage inductance for 12/3-phase dual-winding induction generator[J].Proceedings of the CSEE，2007，27(21)：71-75.

[17]吳新振，王祥珩.12/3相雙繞組異步發電機定子端部漏抗的計算[J].中國電機工程學報，2007，27(24)：80-84.

Wu Xinzhen，Wang Xiangheng.Calculation of stator end-winding leakage inductance for 12/3-phase dual-winding induction generator[J].Proceedings of the CSEE，2007，27(24)：80-84.

[18]王善銘，王祥珩，李義翔，等.交直流混合供電發電機定子繞組端部漏電感的計算[J].電工技術學報，2001，16(2)：1-5.

Wang Shanming，Wang Xiangheng，Li Yixiang，et al.Calculation of stator end winding leakage inductance synchronous generators with AC and DC stator connections[J].Transactions of China Electroechnical Society，2001，16(2)：1-5.

[19]李槐樹，李朗如.多相交流電機端部漏感系數的計算與測量[J].華中理工大學學報，2000，28(9)：34-37.Li Huaishu，Li Langru.The calculation and measurement of end-winding leakage inductance of multiphase electric machines[J].Journal of Huazhong University of Science and Technology，2000，28(9)：34-37.

[20]佟文明，吳勝男，安忠良.基于繞組函數法的分數槽集中繞組永磁同步電機電感參數研究[J].電工技術學報，2015，30(13)：150-157.

Tong Wenming，Wu Shengnan，An Zhongliang.Study on the inductance of permanent magnet synchronous machines with fractional slot concentrated winding based on the winding function method[J].Transactions of China Electrotechnical Society，2015，30(13)：150-157.

[21]付豐禮，唐孝鎬.異步電動機設計手冊[M].北京：機械工業出版社，2002：42-51.

[22]Boldea I，Nasar S A.The induction machine handbook[M].Boca Raton：CRC Press，2002：137-162.

Calculation of Stator Leakage Reactance of Fifteen-Phase Induction Motor Under Symmetrical Fault Condition

Zheng Xiaoqin1Wang Dong2

(1. College of Electrical and Electronic EngineeringHuazhong University of Science and Technology Wuhan430074China 2. National Key Laboratory for Vessel Integrated Power System Technology Naval University of EngineeringWuhan430033China)

To analyze the operation performance of multiphase induction motors under symmetrical fault condition，the stator leakage reactance in the equivalent circuit should be predicted. The stator slot leakage reactance，harmonic leakage reactance and，end-winding leakage reactance of the fifteen-phase induction motor are analyzed using an incidence matrix model to reflect the five-phase and ten-phase open-circuited fault operation. The analysis results indicate that the stator slot leakage reactance is unchanged and the harmonic leakage reactance is increased，while the end-winding leakage reactance is reduced for fifteen-phase induction motor with full-pitch concentrated stator winding under five-phase and ten-phase open-circuited conditions. Thus，there is no exact integer relationship of the stator leakage reactance between symmetrical fault and normal condition. The short-circuit reactances of a prototype fifteen-phase induction motor are measured with locked-rotor test under normal and ten phases opened-circuited conditions. The analytically predicted results are compared with the measured results，where good agreements are achieved.

Fifteen-phase induction motor，symmetrical fault condition，equivalent circuit，stator leakage reactance

2015-04-24改稿日期2015-10-01

TM343

鄭曉欽女，1985年生，博士研究生，研究方向為多相感應電機運行性能分析。

E-mail：zhengxiaoqin619@sina.com

王東男，1978年生，教授，博士生導師，研究方向為電力推進、獨立電源系統等。

E-mail：wangdongl@vip.sina.com(通信作者)

國家重點基礎研究發展(973)計劃(2013CB035601)和國家自然科學基金(51222705，51207163)資助項目。