方位大失準角下基于時變參數(shù)的捷聯(lián)羅經(jīng)對準方法

肖遼亮

（湖南鐵道職業(yè)技術(shù)學院 湖南 株洲　412001）

方位大失準角下基于時變參數(shù)的捷聯(lián)羅經(jīng)對準方法

肖遼亮

（湖南鐵道職業(yè)技術(shù)學院 湖南 株洲412001）

傳統(tǒng)的羅經(jīng)對準方法都是建立在小失準角的基礎(chǔ)上進行的快速對準方式。但是始對準技術(shù)是由于風浪、設(shè)備誤差或者低精度的粗對準算法等不確定因素的影響，捷聯(lián)慣導系統(tǒng)有時候不得不在大失準角下進行羅經(jīng)對準。本文提供了一種時變羅經(jīng)對準方法，以解決此種方位大失準角情況下的羅經(jīng)對準問題。仿真結(jié)果表明，相對于傳統(tǒng)的羅經(jīng)對準方法，時變羅經(jīng)對準方法能夠在方位大失準角下快速而精確的完成初始對準。

光纖陀螺捷聯(lián)慣導系統(tǒng)；初始對準；大失準角；時變參數(shù)

初始對準技術(shù)是捷聯(lián)慣導系統(tǒng)的關(guān)鍵技術(shù)之一，初始對準過程的準確性和效率性會直接影響到捷聯(lián)慣導系統(tǒng)的整體性能。在實際的應(yīng)用過程中，絕大部分情況下都要求捷聯(lián)慣導快速準確的完成初始對準［1-2］。

基于羅經(jīng)效應(yīng)的羅經(jīng)對準方法被廣泛的應(yīng)用于完成捷聯(lián)慣導系統(tǒng)的初始對準過程。但是，目前的捷聯(lián)羅經(jīng)初始對準都是應(yīng)用到方位小失準角情況下，即粗對結(jié)束后，初始方位失準角在3°以下［3］。否則，系統(tǒng)模型會變成非線性的，而此時傳統(tǒng)的捷聯(lián)羅經(jīng)對準方法將達不到快速準確的對準要求。

捷聯(lián)慣導系統(tǒng)的粗對準需要利用到陀螺測量到的地球自轉(zhuǎn)角速度以及加速度計測量的地球引力。但是在某些情況下，比如船體處于搖擺情況下，船體的測量數(shù)據(jù)可能會受到干擾角速度和線性運動的影響。這些干擾量和慣性測量設(shè)備的隨機誤差一樣，會導致粗對準結(jié)果無法達到預(yù)期要求，從而形成方位大失準角情況［4-6］。因此需要解決在方位大失準角情況下的捷聯(lián)羅經(jīng)對準。

在文中設(shè)計了一種基于時變參數(shù)的捷聯(lián)羅經(jīng)對準方法，該方法能夠在對準的不同階段選擇不同的對準參數(shù)來完成對準，從而解決了方位大失準角角情況下的捷聯(lián)羅經(jīng)對準。

1　方位大失準角情況下的系統(tǒng)模型

1.1方位大失準角對準原理圖

方位大失準角對準系統(tǒng)如圖1所示，大失準角情況下，方位對準回路中，方位失準角與水平失準角的關(guān)聯(lián)項為

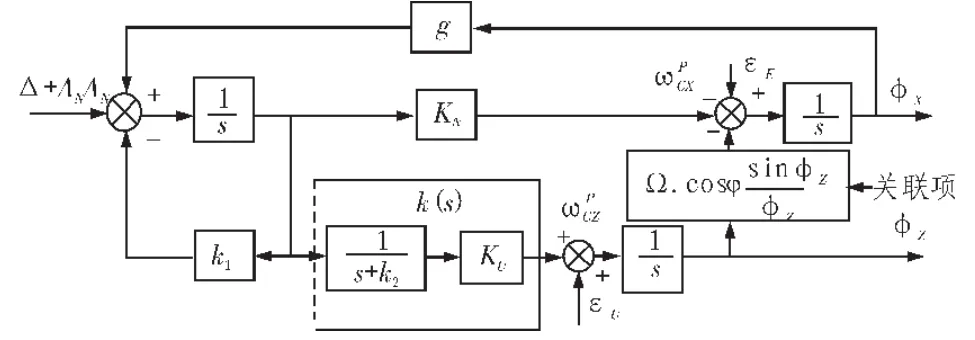
圖1　大失準角下羅經(jīng)對準原理圖

1.2參數(shù)選擇

針對北向水平回路進行展開分析。以δVN、φx和φz為狀態(tài)，可得出靜基座條件下的方程：

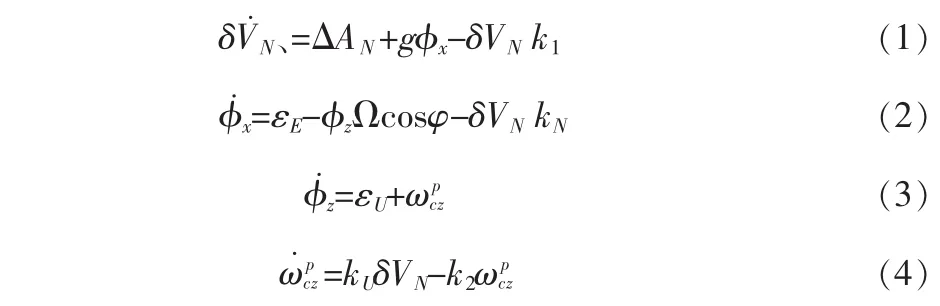
將式（1）至（4）轉(zhuǎn)化為頻域形式：

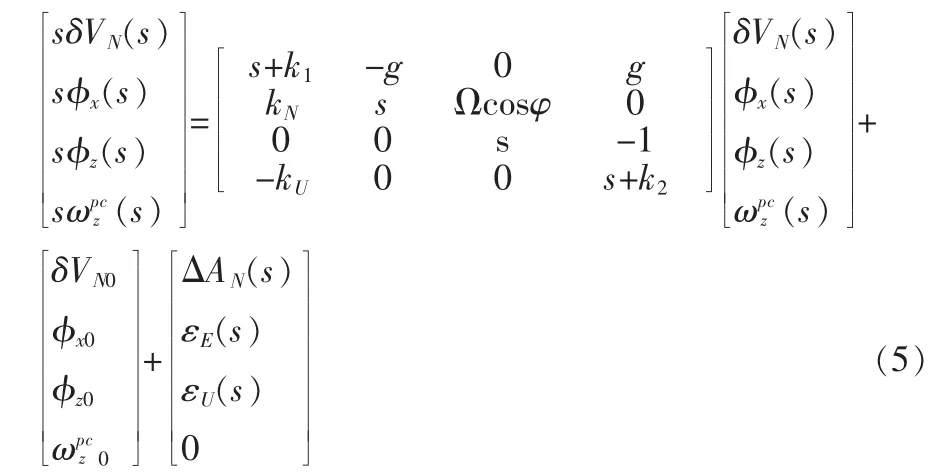
通過方程（5）求解狀態(tài)值，狀態(tài)值求解的結(jié)果為

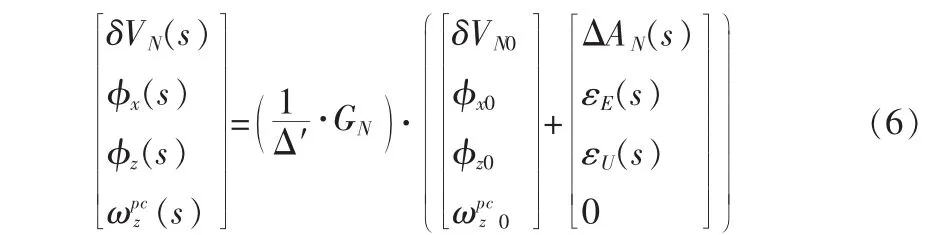
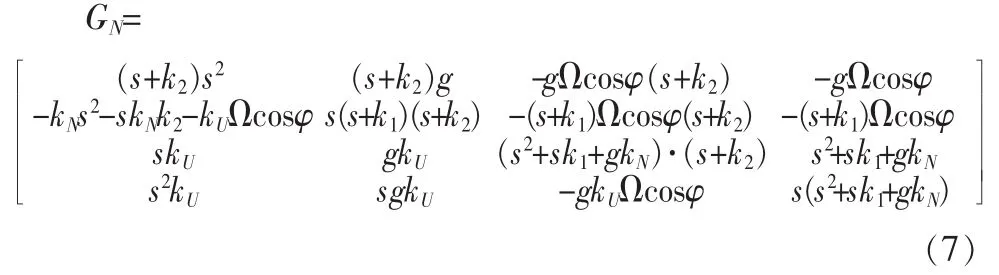
其中，

Δ′表示特征式，則系統(tǒng)的特征方程為：

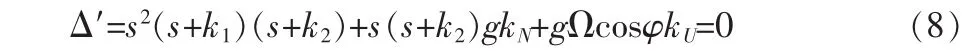
從特征方程可知系統(tǒng)為有阻尼形式，只有合理地設(shè)置系統(tǒng)參數(shù)k1、k2、kN和kU的值，系統(tǒng)即可被設(shè)計為穩(wěn)定系統(tǒng)。為了保證系統(tǒng)穩(wěn)定，取系統(tǒng)的4個特征根為s1，2=-ξωn，s3，4=-ξωn+，其中ξ為阻尼系數(shù)，ωn為無阻尼振蕩頻率［4-5］。系統(tǒng)特征方程又可寫為：

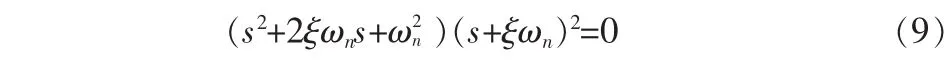
比較式（8）與（9），可知系統(tǒng)參數(shù)可按如下方式設(shè)定：

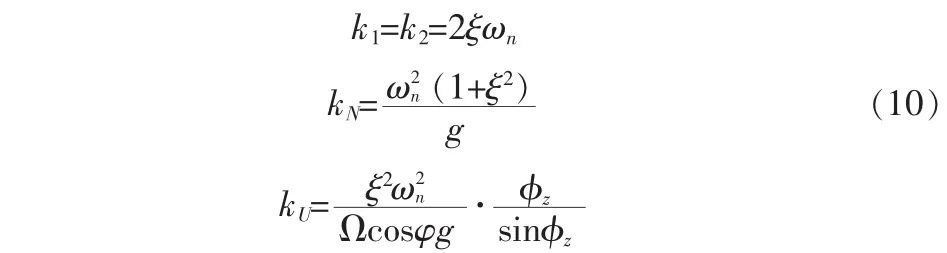
實際上，方位失準角φz在對準過程中是未知的，只能設(shè)置：

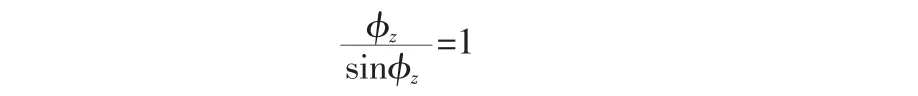
因此，

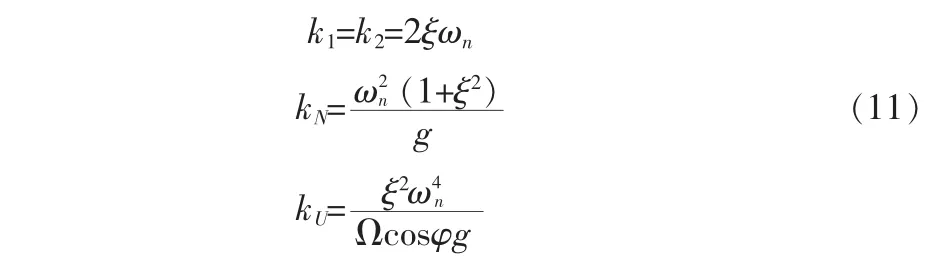
在大失準角和小失準角下，按式（11）來設(shè)置系統(tǒng)參數(shù)。在方位大失準角情況下，此時參數(shù)設(shè)置已經(jīng)不能達到最優(yōu)效果，因此在對準過程中必須引入一些新的參數(shù)設(shè)置辦法來解決這個問題。

2　自然振蕩頻率在對準過程中影響

從圖1中，可以得到ΔAN+AN+gφz從關(guān)聯(lián)到修正角速度ωpcz的信號流程圖如圖2所示。

圖2　修正角速度的信號流程圖

對于式（3）和式（4）兩種參數(shù)設(shè)置方式而言，在對準過程中，所關(guān)聯(lián)的修正角速度也是不同的。在大失準角情況下，φz/sinφz＞1，而不是φz/sinφz=1。此時實際應(yīng)用的參數(shù)設(shè)置方式（4），系統(tǒng)參數(shù)ku在對準過程中小于最優(yōu)參數(shù)ku。因為在圖2的流程圖中，ku是前向增益，所以這導致實際的修正角速度也小于最優(yōu)角速度。通常來說，修正角速度的減小會延長對準周期，影響對準時間。因此，需要通過調(diào)節(jié)其他的系統(tǒng)參數(shù)來消除大失準角情況帶來的不利影響。

系統(tǒng)流程圖和參數(shù)的設(shè)置過程中發(fā)現(xiàn)有兩個可設(shè)置參數(shù)可以影響到ku的取值。分別為阻系數(shù)ξ和系統(tǒng)自然振蕩頻ωn。但是在實際的工程應(yīng)用中，阻尼系數(shù)一般取值為0.707。所以一般情況下，只能夠用過調(diào)節(jié)系統(tǒng)自然振蕩頻率ωn來影響ku的取值，從而解決大失準角情況下的對準問題。

把參數(shù)設(shè)置方式（11）代入圖2中，可以得到如下的增益方程：

從上面的增益方程，可以得知系統(tǒng)自然振蕩頻率ωn直接影響到系統(tǒng)的修正角速。系統(tǒng)角速度隨著ωn的增大而增大，此時系統(tǒng)的對準周期明顯的縮短。

下面來分析ωn的增大對系統(tǒng)帶來的負面影響。根據(jù)圖1和式（11），可以得到如下的系統(tǒng)方程

然后，可以畫出相關(guān)的BODE，給出傳遞函數(shù)的幅頻特性。

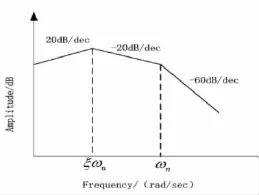
圖3　BODE圖

從圖3，可以得知，當阻尼系數(shù)ξ為常數(shù)的情況下，調(diào)節(jié)ωn可以影響振幅增益。振幅增益會隨著ωn的增長而增長。即，ωn的增長會導致周期性擾動加速度的影響被加強，從而影響系統(tǒng)的魯棒性。

根據(jù)上面的分析，當加大自然振蕩頻率ωn的值，既會給系統(tǒng)帶來積極影響，也會給系統(tǒng)帶來消息影響。

3　參數(shù)切換方案

因為加大自然振蕩頻率ωn的值，既會給系統(tǒng)帶來積極影響，也會給系統(tǒng)帶來消息影響。所以應(yīng)該在對準的不同階段選擇不同ωn值來滿足對準要求。在對準的初始階段，需要一個較大的ωn值來加快對準過程，迅速調(diào)節(jié)失準角。但是在對準的借宿階段，需要一個較小的ωn值來增加系統(tǒng)的穩(wěn)定性，此時需要在對準過程中進行參數(shù)切換。

3.1參數(shù)切換誤差

從式（11）可得知，改變自然振蕩頻率ωn的值會改變系統(tǒng)參數(shù)k1，k2，kN和kU的值。下一步將要分析參數(shù)切換對這些系統(tǒng)參數(shù)的影響。

以系統(tǒng)參數(shù)為k1例，假設(shè)參數(shù)切換之前參數(shù)切換之后根據(jù)圖1的系統(tǒng)流程圖，可以得到如下的速度誤差方程：

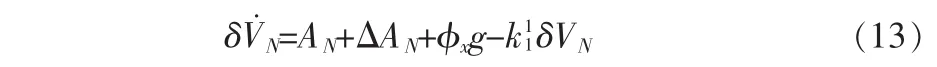
參數(shù)切換之后

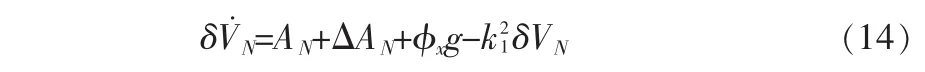
假設(shè)

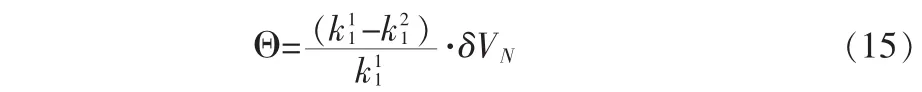
式（14）可以從新寫為

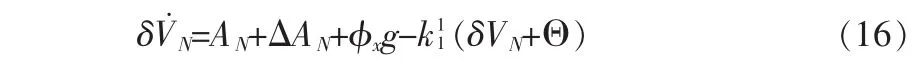
比較式（13）和式（16），可以發(fā)現(xiàn)參數(shù)k1的切換等效為一個脈沖響應(yīng)加在羅經(jīng)對準過程中。通過式（16）的進一步分析，可以知道脈沖響應(yīng)的強度與參數(shù)切換的幅值直接相關(guān)。但是脈沖響應(yīng)會在羅經(jīng)對準過程中引起系統(tǒng)的超調(diào)從而直接影響對準的性能表現(xiàn)。因此，需要設(shè)計合適的參數(shù)切換方式。

首先，考慮了兩種參數(shù)切換模式，一種為脈沖響應(yīng)，一種為斜坡響應(yīng)。根據(jù)圖1的系統(tǒng)流程圖，可以得出傳遞函數(shù)，并且可得到加在方位失準角上面的脈沖響應(yīng)和斜坡響應(yīng)。

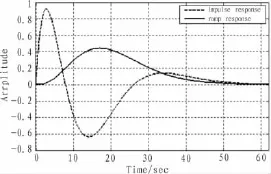
圖4　脈沖響應(yīng)和斜坡響應(yīng)

圖4的響應(yīng)結(jié)果是建立在自然振蕩頻率以兩種不同的方式從ω1=0.2變到ω2=0.1的情況下。從圖中，可以得知，脈沖響應(yīng)的峰值時斜坡響應(yīng)的兩倍。并且斜坡響應(yīng)的收斂速度明顯快于脈沖響應(yīng)。所以可以得出結(jié)論，斜坡響應(yīng)比脈沖響應(yīng)在對準中有著更好的過程表現(xiàn)。根據(jù)式（11），可知，其他參數(shù)（k2，kN和kU）的切換誤差形式上和k1一樣，故其結(jié)論也一樣。

3.2時變方案

從第三節(jié)我可知在對準初期需要一個較大的自然振蕩頻率ω，在對準后期需要一個較小的自然振蕩頻率ω。故不可避免的需要在對準過程中進行參數(shù)切換。

觀察式（10）和式（11），發(fā)現(xiàn)最優(yōu)參數(shù)和實際參數(shù)的差距主要在ku的取值。相差為倍。在小失準角情況=1下，此時實際參數(shù)即為理想?yún)?shù)，但是在大失準角環(huán)境下，，此時實際參數(shù)和理想?yún)?shù)的差距與失準角φz有關(guān)。設(shè)，其對應(yīng)關(guān)系如圖5所示。

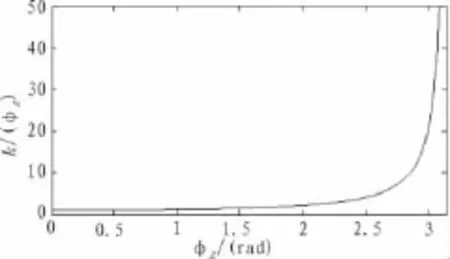
圖5　對應(yīng)曲線

根據(jù)實際工程經(jīng)驗，在對準的穩(wěn)態(tài)階段，要求如下：

1）由晃動引起的方位失準角的振蕩幅值小于3角分；

2）北向干擾加速度的幅值為an=5×10-3m/s2。

方位失準角與北向干擾加速度的幅值比為:

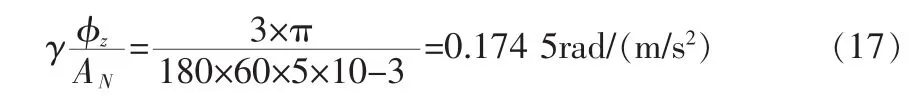
根據(jù)式（12），可以得到系統(tǒng)的傳遞函數(shù)為

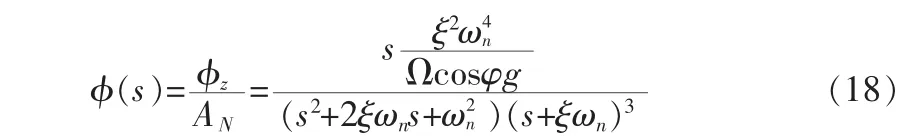
在一般的工程應(yīng)用中，在對準的后期階段設(shè)置ω=0.01以確保系統(tǒng)的穩(wěn)定性。從上圖中，可知，在一般的失準角情況下k（ωz）成線性變化。

在實際情況下，就算為大失準角環(huán)境下，系統(tǒng)的方位失準角也不會超過15度而在初始方位失準角為15的時候，實際值與小失準角情況下理想值的倍數(shù)為：

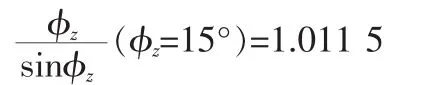
根據(jù)式（10），在大失準角環(huán)境下所取的kU值比理想情況下應(yīng)該取的kU值小1.011 5倍，所以需要調(diào)節(jié)其他的參數(shù)來使kU增大1.011 5倍以達到較好的對準效果。

根據(jù)式（10），可調(diào)節(jié)的參數(shù)有阻尼系數(shù)ξ和自然振蕩頻率ωn，由于阻尼系數(shù)ξ在工程應(yīng)用過程中保持常值，故需要調(diào)節(jié)自然振蕩頻率ωn使kU值增大1.011 5倍，由于式（10）中ωn為四次方，而故時變斜率取值為0.002 9。

時變時間我們設(shè)置為1分鐘，經(jīng)過計算，初期應(yīng)該設(shè)置ω1=0.184。

另外，發(fā)現(xiàn)斜坡響應(yīng)在羅經(jīng)對準過程中有著較好的表現(xiàn)。所以，在對準初期設(shè)置ω1=0.184，在對準末期設(shè)置ω2=0.01，并且選擇斜坡函數(shù)進行時變切換。

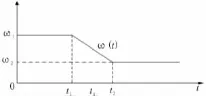
圖6　時變方案

在ω1和ω2之間，時變函數(shù)為

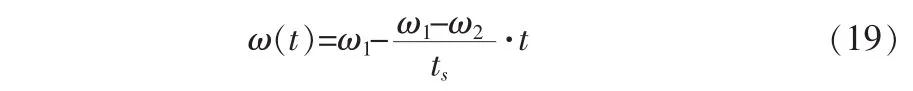
其中ts∈（t1，t2）.該參數(shù)切換方法稱之為時變方法，是一種可以處理方位大失準角情況的羅經(jīng)對準方法。

4　理論仿真及實際試驗結(jié)果

通過Matlab軟件對理論結(jié)果進行仿真，在仿真環(huán)境下對各個羅經(jīng)對準方案進行理論仿真并比較，仿真的器件誤差參數(shù)設(shè)置如下:

陀螺漂移:0.01 deg/h

陀螺測量噪聲:0.005 deg/h1/2

加速度計零偏:10-4g

加速度計測量噪聲:10-5g

此外，初始方位角為135度。初始水平失準角均為0.1度，初始方位大失準角設(shè)置為10度，此時初始狀態(tài)為大失準角情況，所以對準階段必須按照大失準角情況考慮。3種對準方案設(shè)計如下：

方案1（i1）:使用常量自然振蕩頻率ω1=0.184

方案2（i2）:在對準初期設(shè)置ω1=0.184，在對準末期設(shè)置ω2=0.01，此時將會在羅經(jīng)對準過程中造成一個脈沖響應(yīng)。

方案3（i3）:在對準初期設(shè)置ω1=0.184，在對準末期設(shè)置ω2=0.01，并且在兩個參數(shù)之間使用時變函數(shù)ω（t）進行參數(shù)切換，此時將會在羅經(jīng)對準過程中造成斜坡響應(yīng)。

在羅經(jīng)精對準之間，已經(jīng)先進行了2分鐘的粗對準，所以3種對準結(jié)果將不會考慮粗對準過程，采樣頻率設(shè)置為10 Hz.

仿真結(jié)果如圖7所示。Y軸為方位角，X軸為對準時間。3條對準曲線分別表現(xiàn)了3種對準方案從初始的大失準角情況下收斂到穩(wěn)態(tài)的過程。在整個對準過程中，3種對準方案有著相同的穩(wěn)態(tài)精度，但是方案3的收斂速度明顯快于方案1和方案2，并且方案3和方案2比起來，超調(diào)不明顯，綜合分析，方案3為最優(yōu)方案，它能在20分鐘內(nèi)完成對準過程。

方位失準角分別為1度、3度以及5度情況下3種羅經(jīng)對準方法對準時間的統(tǒng)計如表1所示。

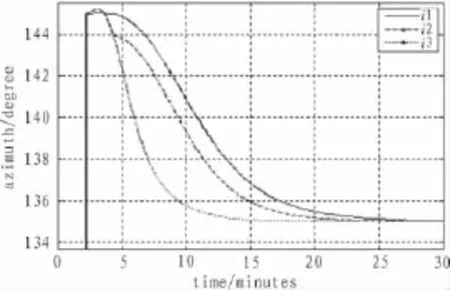
圖7　仿真結(jié)果

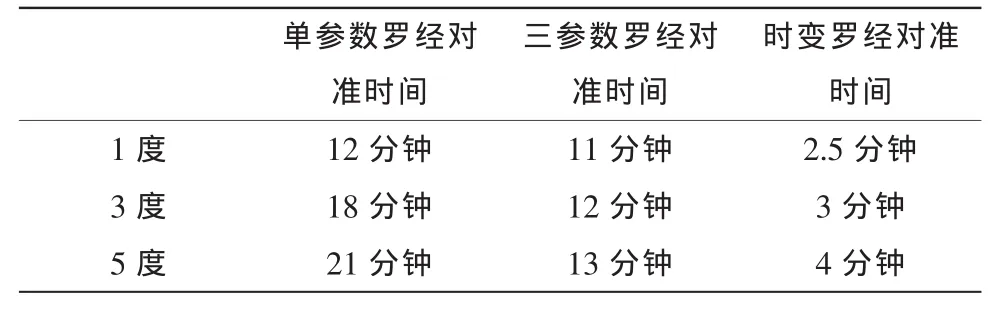
表1　3種羅經(jīng)對準方法對準時間

從統(tǒng)計表中可得知，時變羅經(jīng)對準方法達到穩(wěn)態(tài)所用的時間較其他兩種方法更短，并且失準角越大，時變羅經(jīng)對準方法的優(yōu)勢越明顯。在相對較小的失準角情況下時變羅經(jīng)也有不錯的表現(xiàn)。

為了進一步的證明理論的正確性，我們在松花江上進行了實際的試驗。捷聯(lián)光纖陀螺導航系統(tǒng)為哈爾濱工程大學自產(chǎn)，系統(tǒng)參數(shù)如表2。

表2　TABLE 1 INS參數(shù)性能

其中一個INS/GPS的輸出數(shù)據(jù)作為本次試驗的基準數(shù)據(jù)。基準數(shù)據(jù)和試驗數(shù)據(jù)都被保存下來進行離線的數(shù)據(jù)分析。

3種方案的對準時間均為30分鐘，對準結(jié)果如下：

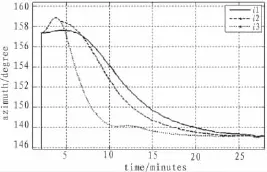
圖8　試驗結(jié)果

根據(jù)圖9，可知，方案3有著最優(yōu)的對準結(jié)果。當使用方案3時，獲得了最快的收斂速度和最合理的參數(shù)切換誤差。在20分鐘左右的時候完成了對準。

5　結(jié)　論

在大失準角下，傳統(tǒng)的捷聯(lián)羅經(jīng)對準方法對準時間延長，對準不滿足快速定位的要求。文中給出了一個隨時間變化的羅經(jīng)對準方法，在對準階段不同，使用不同的自然頻率，將一個斜坡函數(shù)引入到參數(shù)切換時刻。仿真和實驗結(jié)果表明，該方法可以在20分鐘內(nèi)完成精對準，實驗結(jié)果證明了所提出的方法的正確性。

［1］夏家和，秦永元，賈繼超.大失準角下基于交互模型的慣導快速對準［J］.信息與控制，2010（2）:1002-1004.

［2］劉海鵬，張科，李恒年，等.捷聯(lián)慣導系統(tǒng)大失準角下的初始對準研究［J］.航空計算技術(shù)，2012（7）:39-42.

［3］嚴恭敏，翁摘 浚，白亮，等.基于慣性參考系的動基座初始對準與定位導航［J］.系統(tǒng)工程與電子技術(shù)，2011（3）:1001-506x.

［4］張寧.基于UKF的捷聯(lián)慣導大失準角初始對準方法 ［J］.計算機仿真學報，2011（6）:1006-9348.

［5］趙文芳，趙偉，錢偉行.SUKF濾波在SINS大失準角初始對準中的應(yīng)用研究［J］.光電與控制，2008（9）:84-86.

［6］蔣龍嬌.UKF煤礦井下捷聯(lián)慣導大失準角初始對準應(yīng)用研究［D］.北京：中國礦業(yè)大學，2014.

A time-varying gyrocompass alignment method for SINS based on large azimuth misalignment

XIAO Liao-liang
（Hunan Railway Professional Technology College，Zhuzhou 412001，China）

Conventional strapdown gyrocompass alignment systems are based on relatively small azimuth misalignment angles. However systems may be faced to large azimuth misalignment angles caused by storms，large device errors and low accuracy of the coarse alignment algorithm.This paper provides a new time-varying gyrocompass alignment method that solves the question which the initial azimuth misalignment angle is too lager.And the simulations show that，compared to the conventional gyrocompass method，time-varying gyrocompass can complete the initial alignment quickly and accurately based on large azimuth misalignment angle.

SINS；coarse alignment；error auto-compensation；large misalignment angle；time-varying parameters

TN914.3

A

1674-6236（2016）14-0126-04

2015-07-31稿件編號：201507203

肖遼亮（1975—），男，湖南株洲人，碩士研究生，副教授。研究方向:嵌入式系統(tǒng)、機器視覺系統(tǒng)。