小概率 解法多

吳強

?

小概率 解法多

吳強

概率是隨機事件自身的屬性，是對隨機事件發生的可能性大小的度量.概率的計算是中考命題的熱點之一.求概率要根據題目的特點，選擇適用的方法，才能簡捷準確.

一、實驗法

在多次重復試驗中，一個隨機事件發生的頻率會在某一個常數附近擺動，并且隨著試驗次數增多，擺動的幅度會減小.當試驗次數很大時，事件發生的頻率可以作為其概率的估計值.

例1在一個不透明的口袋里裝有黑、白兩種顏色的球共20只，某學習小組做摸球實驗，將球攪勻后從中隨機摸出一個球記下顏色，再把它放回袋中，不斷重復.下表是活動進行中的一組統計數據：

（1）請估計：當n很大時，摸到白球的頻率將會接近_______；（精確到0.01）

（2）假如你去摸一次，你摸到白球的概率是________，摸到黑球的概率是_______；

（3）試估算口袋中黑、白兩種顏色的球各有多少只.

（4）解決了上面的問題，小明同學猛然想起過去一個懸而未決的問題：在一個不透明的口袋里裝有若干個白球，在不允許將球倒出來數的情況下，如何估計白球的個數（可以借助其他工具及用品）？請你應用統計與概率的思想和方法解決這個問題，寫出主要步驟及估算方法.

解：（1）當n很大時，摸到白球的頻率將會接近（0.58+0.64+0.58+0.59+0.605+0.601）÷ 6≈0.60；

（2）摸到白球的概率是0.60，摸到黑球的概率是1-0.60=0.4；

（3）白球有20×0.60=12（只），黑球有20-12=8（只）；

【總結】考查利用頻率估計概率，大量重復試驗下，頻率的穩定值即概率.用到的知識點為：概率=所求情況數與總情況數之比.部分數目=總體數目乘相應概率.

二、枚舉法

例2在數字1，2，3中任選兩個組成一個兩位數，則這個兩位數能被3整除的概率是________.

【分析】根據概率的求法，找準兩點：①全部等可能情況的總數；②符合條件的情況數目.二者的比值就是其發生的概率.

練習用2、3、4三個數字排成一個三位數，則排出的數是偶數的概率為_______.

例3甲、乙、丙三位同學隨機站成一排照合影，甲沒有站在中間的概率為_______.

【分析】枚舉出所有情況，看甲沒排在中間的情況占所有情況的多少即為所求的概率.

【總結】本題考查用枚舉法求概率，用到的知識點為：概率等于所求情況數與總情況數之比.

三、方程法

例4不透明的口袋中裝有若干個完全相同的白球，為了估計它們的個數，現將兩個黑球（除顏色外其他都與白球相同）放入口袋中，然后從口袋中隨機摸出一個球，記下顏色后再放回口袋中，按此方法摸了100次，有20次摸到了黑球，則估計口袋中共有白球（）.

A.7個B.8個C.9個D.10個

【分析】口袋中有2個黑球，根據黑球在總數中所占比例與實驗比例相等求出即可.

解：（1）設有x個白球，

∵口袋中有2個黑球，實驗總共摸了100次，其中有20次摸到了黑球，

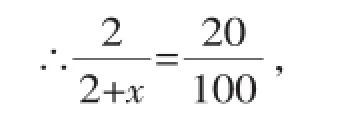
解得：x=8，即口袋中有白球8個.故選B.

例5在一個不透明的袋子中裝有僅顏色不同的10個小球，其中紅球4個，黑球6個.

（1）先從袋子中取出m（m>1）個紅球，再從袋子中隨機摸出1個球，將“摸出黑球”記為事件A.請完成下列表格：

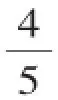
解：（1）事件A為必然事件，則袋中應全為黑球，∴m=4；若事件A為隨機事件，則袋中有紅球，∵m>1，∴m=2或3.

（作者單位：江蘇省常州外國語學校）