面向可靠性設計優化的響應面偏差修正方法

詹振飛　楊俊祺　舒雅靜　楊仁杰

1.重慶大學機械傳動國家重點實驗室，重慶，4000442.美國福特汽車研究院被動安全部門，密西根州，美國，48124

?

面向可靠性設計優化的響應面偏差修正方法

詹振飛1楊俊祺1舒雅靜1楊仁杰2

1.重慶大學機械傳動國家重點實驗室，重慶，4000442.美國福特汽車研究院被動安全部門，密西根州，美國，48124

在基于仿真的汽車設計中，針對響應面模型普遍存在的精度不高的問題，研究了基于貝葉斯推斷的模型外推預測方法，提出了模型不確定性下基于偏差修正的模型外推及可靠性設計優化方法，并通過一個汽車輕量化設計實例驗證了所提方法的有效性。

響應面；偏差修正；可靠性設計優化；模型外推

0　引言

在基于仿真的汽車設計過程中，不考慮設計變量的不確定性將直接影響設計性能指標的可靠性，從而不能滿足實際使用要求。因此，考慮仿真模型固有不確定性的可靠性設計技術至關重要。可靠性設計優化(reliability-based design optimization, RBDO)[1-3]方法是一種在參數化設計過程中考慮設計變量等不確定性因素及其對目標和約束函數影響的一種設計優化技術。可靠性設計優化一般包括三方面內容：質量、成本與可靠度。考慮各種不確定性因素對性能參數的影響，將可靠性設計優化方法應用到汽車設計過程中，既能保證產品的經濟效益，又確保產品實際運行中的安全可靠性。

在實際的優化設計過程中，基于仿真模型的優化迭代是優化過程中的核心步驟。隨著有限元(finite element, FE)技術的迅速發展，基于高精度FE模型的設計成為各大汽車企業解決復雜設計問題的一種有效工具。然而，即使計算機運算能力不斷增強，通過高精度有限元模型進行優化仍然會花費大量時間。此外，RBDO過程包含兩層嵌套循環，優化迭代需要同時在設計域以及設計變量不確定性空間中進行。將FE模型用于需要成千上萬次迭代的RBDO中顯得不切實際。

為了縮短開發時間，基于數學表達式的響應面模型(response surface model,RSM)常被用于替代要求大量計算時間的有限元模型。多年來，學者們開發和改進了多種RSM[4-6]。然而，無論采用哪種RSM建模技術，在實際FE模型和RSM之間始終會有偏差。特別是當RSM模型用于外推來預測新設計時，偏差的影響尤其顯著。

模型更新方法不但可以量化數據不確定性大小，而且可以進一步提高模型的預測能力。目前該方法在模型驗證領域取得較快發展，已成為國內外研究的前沿和熱點[7-17]。

目前，大多傳統基于RSM的RBDO未考慮來自于數值模型的不確定性，該RBDO過程在RSM能精確預測高精度FE模型輸出的假設下進行。而在實際運用中，若模型精度不高且受大量不確定性影響時，RBDO將難以得到可靠的優化解。因此，在執行RBDO尋優前運用模型更新技術對模型偏差進行修正至關重要。

本文首先介紹基于貝葉斯推理的偏差修正方法，然后提出一種基于響應面模型偏差修正的RBDO流程，最后通過一個汽車輕量化設計實例說明所提方法的有效性。

1　基于貝葉斯推理的偏差修正

Zhan等[11,18]綜合貝葉斯推斷理論的優勢和響應面模型的缺陷，提出了一種基于貝葉斯推理的模型外推預測方法。首先根據設計空間中的試驗設計(design of experiment，DOE)矩陣運行相應的CAE仿真及響應面仿真，二者之間的差作為偏差先驗信息。得到先驗分布后，基于貝葉斯推理預測偏差超參數(hyper-parameter)的后驗分布。

令x表示設計變量，Yf和Ym分別代表FE和RSM模型輸出。ε表示隨機誤差，δ表示響應面模型與FE仿真模型間的偏差。因此輸出的“真實值”，即Yture，等于FE仿真輸出值減去隨機誤差，同時也等于響應面模型預測值加上模型偏差，表達式如下：

Ytrue=Yf(x)-ε(x)=Ym(x)+δ(x)

(1)

因此， Yf(x) 和Ym(x)之間的關系可進一步描述為

Yf(x)=Ym(x)+δ(x)+ε(x)

(2)

在式(2)中，假設偏差τ(x)=δ(x)+ε(x)服從一個已知方差的正態分布:

(3)

θ～N(μ,σ2)

(4)

對偏差均值進行正態分布的假設是出于兩方面的考慮。一方面，正態分布是一種常見且合理的偏差假設。特別是當樣本數量足以滿足大數定律等要求時，觀測量常近似于正態分布。另一方面，在貝葉斯理論中，當后驗分布p(θ|x)與先驗分布p(θ)為相同分布時，則稱先驗分布與似然函數是共軛的，而正態分布是一種常見的有共軛性質的分布類型。在該假設下，貝葉斯推斷過程難度將極大降低。因此，不論從合理性角度還是推導難度角度考慮，正態分布都是一種理想的假設。

根據貝葉斯理論，后驗分布等于似然函數與先驗分布p(θ)的乘積除以p(x)的全概率，表達式如下：

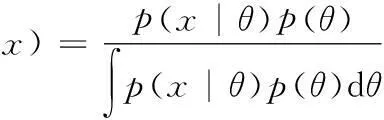
(5)

式(5)中分母全概率可寫作：

∫p(x|θ)p(θ)dθ=

(6)

其中，n表示在每一個設計點處的樣本數。從而根據共軛性質，式(5)可進一步表示為一個正態分布，表達式為

(7)

因此，θ后驗分布可表示為

(8)

基于所得每一個設計點處的后驗偏差分布，分別為預測偏差的均值和標準差建立一個響應面。得到外推域新設計的響應面預測結果后，根據均值和方差響應面計算偏差預測結果的置信度區間。結合原始低精度響應面預測結果以及推斷所得的偏差預測區間，響應面的預測能力得以提高。基于所得結果，決策者可以決定接受或者拒絕預測結果。如果接受則進行進一步的可靠性設計優化。若預測結果被拒絕，則增加DOE樣本點重復此過程，直到得到好的預測結果[11]。

2　參數和模型不確定性下的RBDO

RBDO在考慮設計變量不確定性下獲取最優設計方面有其獨特優勢，因此在不確定性下優化設計中被廣泛應用。典型的RBDO數學公式定義如下：

min E[f0(X)]

s.t. P(fi(X)≤0)≥ai,i=1,2,…,k

其中，X為包含不確定性的輸入隨機變量，E[·]代表方程的期望，P(·)為概率，fi(x)為目標函數，ai為可靠度。

然而，基于RSM的RBDO需要考慮來自于數值模型的不確定性，對模型偏差進行修正，以得到可靠的優化解。圖1為綜合考慮變量和模型不確定性的可靠性優化設計示意圖。基于偏差修正響應面的RBDO流程始于對RBDO問題的定義，隨后構建DOE矩陣，基于貝葉斯推理構建的偏差模型用以修正原始RSM。然后，將修正的RSM用于RBDO優化的迭代尋優流程中，以求得到可靠優化解。最后，基于FE模型進行若干次蒙特卡羅仿真(Monte Carlo simulation，MCS)以驗證優化解的可靠性。如果所得優化解滿足各性能指標約束可靠度要求，則此尋優過程完成，否則改善DOE矩陣，反復以上過程直到得到滿意結果。

圖1　可靠性優化設計示意圖

3　實例分析：汽車前部結構設計

所提方法被應用于一個需滿足碰撞安全性能的汽車輕量化設計實例之中。汽車輕量化設計被視為解決目前嚴峻能源危機及環境污染的有效方案之一。然而，輕量化設計絕不僅僅是汽車重量的減輕，它是一個系統性的多學科優化問題。在車重減輕的同時需要保證其他性能，如汽車的耐撞性以及NVH(noise，vibration and harshness)性能等，不會惡化甚至得到一定的提升[19]。目前，通過兩種主要途徑可以實現汽車的輕量化設計。其一是輕量化材料的應用。然而輕質材料的成本以及工藝缺陷是阻礙其發展的最大障礙。另一種途徑是汽車結構的優化，通過零部件的尺寸優化最終實現車重減輕的目的。本文即是將所提優化流程運用于汽車前部結構的優化中，在保證汽車耐撞性的同時實現輕量化設計。在此，美國NCAC(national crash analysis center)的Ford Taurus模型用于驗證本文所提方法的有效性。

正面碰撞是汽車耐撞性評估中最典型的一種碰撞方式。依據美國新車碰撞評估規程(new car assessment program，NCAP)標準，汽車以56.6 km/h的初始速度與剛性墻發生100%正面碰撞。該正碰模型已通過實車碰撞數據與仿真輸出間的比較得以驗證。圖2所示為整車碰撞試驗及CAE仿真變形情況。從比較結果可以看出有限元仿真與物理試驗變形基本一致。因此，該FE模型在優化設計中被視作實車試驗的高精度替代模型，以在其基礎上進行驗證計算。

(a)實車

(b)有限元模型圖2　實車與有限元模型碰撞驗證試驗對比

該模型在擁有32個CPU的高性能計算機上運算一次大約需要5 h。因此，雖然該FE模型能夠保證在優化設計中響應量的預測精度，然而在成千上萬次的優化迭代中基于FE模型尋優顯得不切實際。針對這個問題，所提基于偏差修正響應面的RBDO流程被應用在輕量化設計中。

3.1變量描述及DOE

在正碰耐撞性設計中，車身前部結構的吸能性能直接影響碰撞過程中乘員艙的完整性。合理的車身前部結構設計能夠避免因乘員艙變形過大而對乘員產生嚴重的損傷。圖3所示為選取的車身前部典型構件，將其8個厚度參量作為研究對象。設計變量的范圍以及初始設計值如表1所示。

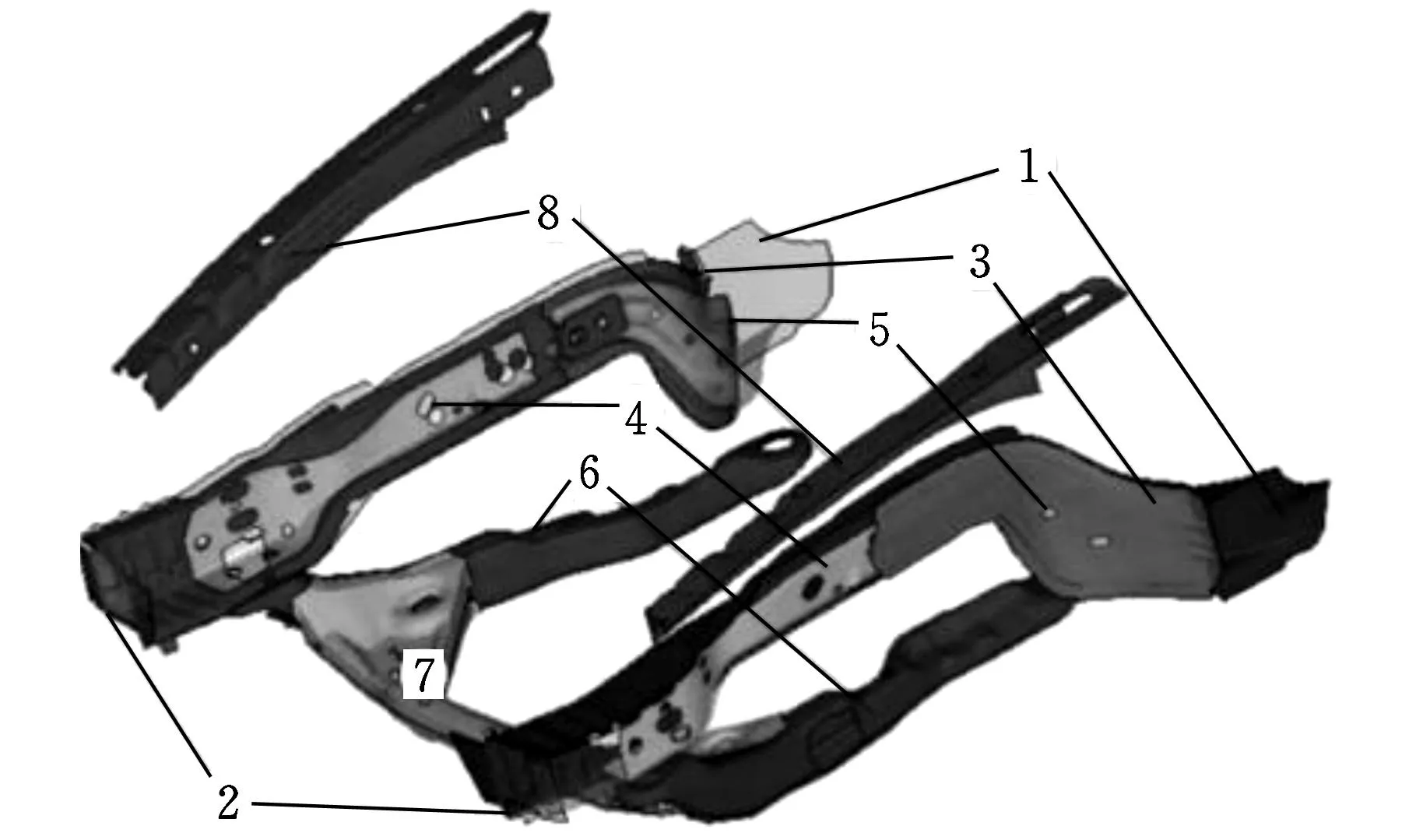
1.發動機艙內側邊梁　2.發動機艙左側外邊梁　3.發動機艙右側外邊梁　4.發動機艙邊梁加強件前端　5.發動機艙邊梁加強件后端　6.副框架內臂　7.副框架前端　8.前指梁圖3　車身前部典型構件

表1　設計變量的范圍及初始設計　mm

根據變量的變化范圍以及變量數目，在設計空間中通過均勻拉丁超立方試驗設計法生成了60組DOE[12,20]。根據生成的60組DOE對FE模型的k文件中對應的關鍵字卡片 (*SECTION_SHELL_TITLE) 中的厚度進行修改。生成的新k文件被提交至高性能運算中心計算。在數據后處理過程中，提取Chest G(假人胸部加速度)以及Crush Distance (整車碰撞有效距離)作為正碰性能響應指標。所提取的數據中前50組DOE樣本用于構建RSM，剩下的10組用于評估外推設計預測精度。

3.2基于修正模型的RBDO

該設計優化的目標是在滿足Chest G(CG)和Crush Distance(CD)的可靠度指標的前提下，通過結構參數的優化減輕車身重量。RBDO的數學表達式如下：

(9)

其中，Uxi和Lxi是設計變量的上下界，Weight是所設計的前部結構總重量。CG和CD的設計目標界限值分別為60g (g為重力加速度)和740 mm，可靠度為98%。根據式(9)可以看出，Weight、CG和CD三個響應量均通過多項式響應面建模技術來近似表示設計變量與響應量間的擬合關系。根據所提方法建立的優化流程如圖4所示。為了比較，分別使用兩種方法進行優化：一種是傳統RBDO，即采用低精度的原始多項式響應面模型進行優化迭代，優化過程中只考慮設計變量的不確定性；另一種是基于修正響應面模型的RBDO，兼顧設計變量的擾動以及響應面模型的固有偏差。

3.3結果與討論

通過多目標遺傳算法(multi-objective genetic algorithm, MOGA),基于未修正模型的修正模型的RBDO分別在第977次和第1189次迭代得到第一組可靠優化解。圖5為以CG為收斂參考指標的迭代圖。由圖可知， 基于未修正和修正RSM模型的優化幾乎同時得到相對穩定的收斂值，收斂效率差別不大。然而，基于未修正模型的優化解即使在達到收斂條件后仍然存在較為劇烈的波動。原始模型的過擬合與欠擬合均能導致這樣的結果。而修正后的模型則呈現出更好的收斂穩定性。由兩種模型所得最終可靠優化解如表2所示。

圖4　汽車前部構件參數RBDO流程

圖5　基于修正和未修正模型的優化迭代

設計變量初始設計RBDO(未修正偏差)RBDO(修正偏差)x1(mm)1.901.691.89x2(mm)1.911.831.83x3(mm)2.512.172.11x4(mm)2.402.542.04x5(mm)2.002.122.06x6(mm)1.802.482.51x7(mm)1.802.092.05x8(mm)1.201.721.70weight(kg)51.9948.9549.40

可以看出，與初始設計相比，基于未修正模型和修正模型的RBDO均得到了輕于51.99 kg的構件，分別為48.95 kg和49.40 kg。若單考慮減重效果，基于未修正模型的RBDO得到的優化解對應的構件重量甚至要低于基于修正模型RBDO的優化解。然而這并不能說明其優化解滿足所要求的可靠性。

為了驗證優化解是否達到可靠性要求，在所得兩組優化解的基礎上，按優化解名義值為均值以及5%均值為標準差的正態分布各生成10組蒙特卡羅樣本，并運行高精度的FE仿真模型計算每個樣本點相應的CG和CD值。如圖6所示，點和星號代表了20個樣本點的仿真結果，圖中的概率密度函數(PDF)為優化迭代中通過修正響應面預測所得優化解的不確定性信息，是設計變量不確定性通過響應面傳遞的結果。圖6a和圖6b分別顯示了CG和CD基于未修正響應面模型和修正模型的RBDO優化解。

(a)CG

(b)CD圖6　基于未修正模型和修正模型的RBDO優化解可靠性驗證

從圖6可以看到，由于未修正偏差的RSM的預測能力有限，CG和CD的預測概率密度分布與10個FE仿真結果偏離過大，其中6個CG的FE仿真以及5個CD的仿真超出了預測分布。此外，CG的10個設計樣本中有1個超出了約束范圍，而CD有4個在約束范圍之外。可以看到，兩個性能響應指標的可靠度都未達到98%。不管是CG還是CD，都是汽車耐撞性評價的重要指標。為了達到相應法規(如NCAP等)的要求，CG和CD的值不僅需要在安全裕度以內，而且還要保證對變量的微小變動不敏感。在實際耐撞性評估試驗中，若該性能指標受環境、材料和工藝等的不確定性因素影響過大，將直接導致耐撞性評估結果不理想，產生巨大的經濟損失。因此，基于未修正模型的RBDO設計無疑是不可行的。在圖6所示基于修正模型的優化解驗證中，10個MC樣本的FE仿真所得結果與隨機偏差修正的RSM相吻合，所有的設計都在CG和CD的正態分布中。兩約束的可靠度均達到設計目標。雖然其減重效果略遜于基于未修正RBDO的優化解，但性能指標的可靠度顯示出基于所提方法進行優化的顯著優勢。

4　結束語

本文介紹了一種基于統計偏差修正的模型外推預測方法，并將其應用到考慮模型和設計變量不確定性的可靠性設計優化流程中。首先運用貝葉斯推理量化模型不確定性,從而修正原始低精度RSM的偏差。然后將修正后的模型用于RBDO過程以尋得可靠的優化解。所提方法通過一個汽車輕量化設計得到闡述。在這個輕量化設計中，考慮整車正面碰撞中的典型耐撞性指標CG和CD的安全約束，使優化設計解滿足設計的可靠性。經對比，基于修正響應面模型的RBDO比傳統的RBDO能保證在實現輕量化的前提下得到可靠度更高的解。

[1]Tu J, Choi K K. A New Study on Reliability Based Design Optimization[J]. ASME Journal of Mechanical Design,1999,121(4):557-64.

[2]白廣忱, 張春宜. 機械系統可靠性優化設計的實現策略[J]. 中國機械工程, 1999,10(8):918-920.Bai Guangchen,Zhang Chunyi.Reliability Based Optimization Design Strategy for Mechanical Systems[J]. China Mechanical Engineering, 1999, 10(8): 918-920. [3]李鐵柱, 李光耀, 高暉, 等. 基于可靠性優化的汽車乘員約束系統的性能改進[J]. 中國機械工程, 2010, 21(8):993-999.

Li Tiezhu, Li Guangyao, Gao Hui, et al. Performance Improvement of Occupant Restraint System Based on Reliability Optimization Method[J]. China Mechanical Engineering, 2010, 21(8):993-999. [4]Viana F A C, Haftka R T, Steffen V J. Multiple Surrogates: How Cross-Validation Errors Can Help Us to Obtain the Best Predictor[J]. Structural and Multidisciplinary Optimization, 2009, 39(4): 439-457.[5]Wang G, Shan S. Review of Metamodeling Techniques in Support of Engineering Design Optimization[J]. Journal of Mechanical Design, 2007, 129(4):370-380.

[6]Zhang S, Zhu P, Chen W, et al. Concurrent Treatment of Parametric Uncertainty and Metamodeling Uncertainty in Robust Design[J]. Structural and Multidisciplinary Optimization, 2012,47:63-76.

[7]Kennedy M C, O’Hagan A. Bayesian Calibration of Computer Models[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2001, 63: 425-464.

[8]Shi L, Yang R J, Zhu P. Adaptive Sampling-based RBDO Method for Vehicle Crashworthiness Design Using Bayesian Metric and Stochastic Sensitivity Analysis with Independent Random Variables[J]. International Journal of Crashworthiness, 2013,18(4):331-342.

[9]張勇 ,李光耀,鐘志華. 基于移動最小二乘響應面方法的整車輕量化設計優化[J]. 機械工程學報,2008, 44(11): 192-196.

Zhang Yong, Li Guangyao, Zhong Zhihua. Design Optimization on Lightweight of Full Vehicle Based on Moving Least Square Response Surface Method[J]. Chinese Journal of Mechanical Engineering,2008, 44(11): 192-196.

[10]劉興堂,劉力,宋坤,等. 對復雜系統建模與仿真的幾點重要思考[J]. 系統仿真學報, 2007, 19(13): 3073-3075.

Liu Xingtang, Liu Li, Song Kun, et al. Important Considerations of Building Pattern to Complicated System[J]. Journal of System Simulation, 2007, 19(13): 3073-3075.

[11]Zhan Z, Fu Y, Yang R J. On Stochastic Model Interpolation and Extrapolation Methods for Vehicle Design[J]. SAE International Journal of Material and Manufacturing, 2013, 6(3):517-531.

[12]Zhan Z, Fu Y, Yang R J, et al.A Bayesian Inference Based Model Interpolation and Extrapolation[J]. SAE International Journal of Material and Manufacturing, 2012, 5(2)：357-364.

[13]Jiang Z, Chen W, Fu Y, et al. Reliability-Based Design Optimization with Model Bias and Data Uncertainty[J]. SAE International Journal of Material and Manufacturing, 2013, 6(3): 502-516.

[14]Xi Z, Fu Y,Yang R J. An Ensemble Approach for Model Bias Prediction[J]. SAE International Journal of Material and Manufacturing,2013,6(3)：532-539.

[15]Ferson S, Oberkampf W L,Ginzburg L. Model Validation and Predictive Capability for the Thermal Challenge Problem[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197(29/32): 2408-2430.

[16]Rebba R,Mahadevan S. Model Predictive Capability Assessment under Uncertainty[J]. AIAA Journal, 2006, 44(10): 2376-2384.

[17]Zhan Z, Fu Y,Yang R J. An Enhanced Bayesian Based Model Validation Method for Dynamic Systems[J].Journal of Mechanical Design, 2011,133(4)：181-189.

[18]Zhan Z, Fu Y, Yang R J. A Stochastic Bias Corrected Response Surface Method and Its Application to Reliability-based Design Optimization[J]. SAE International Journal of Material and Manufacturing, 2014, 7(2):262-268.

[19]Yang R J, Wang N, Tho C H,et al.Metamodeling Development for Vehicle Frontal Impact Simulation[J]. ASME Journal of Mechanical Design, 2005, 127(5):1014-1020.

[20]Shi L, Yang R J, Zhu P. An Adaptive Response Surface Method for Crashworthiness Optimization[J]. Engineering Optimization,2013, 45(11):1365-1377.

(編輯郭偉)

A Bias Corrected Response Surface Method and Its Applications to Reliability-based Design Optimization

Zhan Zhenfei1Yang Junqi1Shu Yajing1Yang Ren-Jye2

1.The State Key Laboratory of Mechanical Transmission,Chongqing University,Chongqing,400044 2.Passive Safety,Research and Innovation Center,Ford Motor Company,Dearborn,MI,USA,48124

In simulation-based vehicle design, the Bayesian inference based model extrapolation method was further investigated,that was previously proposed by the authors, and a systematic bias corrected model extrapolation and RBDO under uncertainty was introduced. A real-world lightweight design problem of vehicle was employed to demonstrate the validity of the proposed method.

response surface；bias-correction; reliability-based design optimization(RBDO); model extrapolation

2015-06-09

國家自然科學基金資助項目(51405041)；汽車噪聲振動和安全技術國家重點實驗室開放課題(NVHSKL-201412)；上海交通大學機械系統與振動國家實驗室開放課題(MSV-2015-11)

U461.7DOI：10.3969/j.issn.1004-132X.2016.07.001

詹振飛，男，1983年生。重慶大學機械傳動國家重點實驗室研究員、博士研究生導師。主要研究方向為模型驗證理論方法、汽車被動安全、多學科優化和穩健設計等。發表論文40余篇。楊俊祺，男，1990年生。重慶大學機械傳動國家重點實驗室博士研究生。舒雅靜，女，1993年生。重慶大學機械傳動國家重點實驗室碩士研究生。楊仁杰，男，1952年生。美國福特汽車研究院被動安全部門首席研究員。