汽車電泳涂裝輸送用新型混聯機構的動力學控制

高國琴　范杜娟　方志明

江蘇大學，鎮江，212013

?

汽車電泳涂裝輸送用新型混聯機構的動力學控制

高國琴范杜娟方志明

江蘇大學，鎮江，212013

由于汽車電泳涂裝輸送用新型混聯機構存在高度非線性和耦合性，因此難以實現高性能控制。為此，首先采用拉格朗日法推導該機構的動力學模型。然后，在任務空間設計一種PD滑模神經網絡動力學控制器并進行穩定性證明。最后，對該控制器進行了仿真，并將所得結果與PD滑模控制器仿真結果進行比較。比較結果表明：該動力學控制器通過神經網絡前饋控制的作用有效解決了PD滑模控制器存在的劇烈抖振問題，使得汽車電泳涂裝輸送控制系統呈現良好的控制性能。

混聯機構；動力學模型；滑模控制；神經網絡控制

0　引言

現有的汽車電泳涂裝輸送系統存在無法實現車體完全涂裝和柔性化水平不高的問題[1]。混聯機構是將串并聯機構合理結合應用的一類機構，不僅可彌補串聯機構在剛度、精度、實時控制等方面的不足，而且可克服并聯機構工作空間小、運動不靈活的缺點[2-4]。本課題組將混聯機構引入汽車電泳涂裝輸送系統，研制了一種新型汽車電泳涂裝輸送用混聯機構[5]。

混聯機構的運動控制方法主要可分為運動學控制方法與動力學控制方法[6-10]。相對于運動學控制方法，動力學控制方法由于考慮了機構運動過程中的非線性動力學特性和力耦合特性，因此在理論上可具有更好的控制性能[7，9]，但動力學控制方法的控制效果依賴于動力學模型的準確性。由于混聯機構所含并聯機構為閉鏈結構并存在運動學約束，因此其動力學模型往往較為復雜。另外，實際控制系統，如汽車電泳涂裝輸送系統，常常存在模型誤差和外界擾動，因此難以建立混聯機構的精確動力學模型。直接基于逆動力學模型設計控制器的計算量較大，難以滿足實時控制要求；傳統的動力學控制方法，如PD控制，算法簡單、計算量小、實時性好，但一般不能有效解決非線性系統模型誤差和外界擾動問題[11-13]，魯棒性較差。

針對實現混聯機構動力學控制的上述問題，學者們提出了魯棒控制方法和智能控制方法[9-12]。魯棒控制方法中，滑模控制對系統模型誤差和外界擾動具有魯棒性，且易于實現，但存在抖振問題，抖振嚴重時難以用于實際工程。智能控制方法中，神經網絡動力學控制能學習與適應不確定系統動態特性，充分逼近任意復雜的非線性映射，且不依賴于動力學參數，并可避免復雜的逆動力學計算，提高了控制系統實時性，但由于是以神經網絡(神經網絡擔負著全部的控制器任務)實現逆動力學計算的，因此對神經網絡初始權值的設置提出了較高要求，且難于根據可測量量調整神經網絡連接權。當出現不確定干擾時，神經網絡對逆系統的逼近能力下降，影響系統控制性能[14]。針對本課題組新研制的汽車電泳涂裝輸送用混聯機構的結構特點以及汽車電泳涂裝輸送工藝要求，為進一步提高其控制性能，提出一種PD滑模神經網絡動力學控制方法，即通過神經網絡實現混聯機構的逆動力學前饋控制，同時通過PD控制實現反饋控制，再通過滑模控制增強混聯機構系統對模型誤差和外界干擾的魯棒性，構成一種新的PD+滑模+神經網絡的復合動力學控制方式。

1　運動學分析及動力學建模

1.1運動學分析

如圖1所示，新型汽車電泳涂裝輸送用混聯機構主要由行走機構與升降翻轉機構兩部分構成，這兩部分機構的控制相對獨立。行走機構通過同步驅動行走輪，實現輸送機的行走平移，其控制相對簡單。作為主體機構的升降翻轉機構為并聯機構，相對較為復雜，且對輸送性能的影響較大，因此本文著重研究升降翻轉機構。

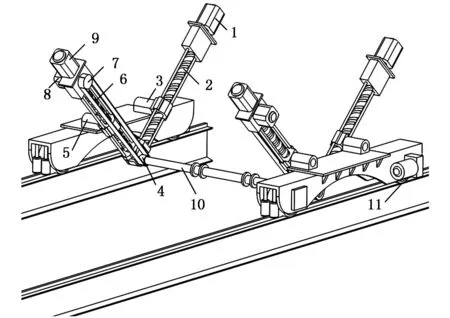
1.第一驅動器　2. 第一絲杠　3. 第一轉動副4.從動輪　5.第二轉動副　6.第二絲杠　7.主動輪8.第三驅動器　9.第二驅動器　10.連接桿　11.行走輪圖1　新型汽車電泳涂裝輸送機構

如圖2所示，升降翻轉機構結構由2個結構完全相同的第一平面多桿機構與第二平面多桿機構構成，為對稱機構，由此，本文針對其單邊機構進行運動學分析與動力學建模。

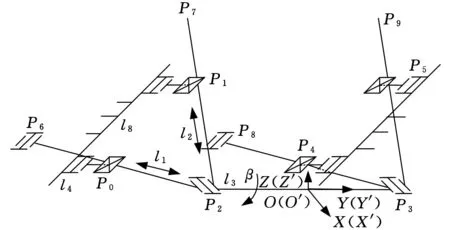
圖2　升降翻轉機構結構簡圖

采用桿長長度約束方程，建立該混聯機構的運動學方程，整理可得其運動學逆解：

(1)

式中，x為連接桿中點在X方向上的位移分量；z為連接桿在Z方向上的位移分量；β為連接桿中點繞Y軸轉過的角度；li(i=1，2)為滑塊P0、P1的移動量；l4為第一連桿和第二連桿的長度(二者相同)；l8為第一、第二轉動副之間的固定距離；φ為主動輪繞Y軸逆時針轉動的角度。

選擇連接桿中點的位姿參數q=[xzβ]T為系統廣義坐標，采用基于符號運算的微分變換法求解混聯機構的雅可比矩陣，具體求解方法如下。

將式(1)兩端分別對時間求導并整理得

(2)

1.2動力學建模

采用拉格朗日法建立該混聯機構的動力學模型。分別求取車體、支鏈、動平臺支架、滑塊、主動輪、從動輪的動能與勢能，根據拉格朗日方程：

(3)

整理并建立標準動力學方程：

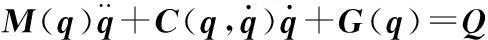
(4)

為了將廣義驅動力轉化為關節驅動力，作如下變換：

Q=JTτ

(5)

式中，J為混聯機構的雅可比矩陣；τ為關節驅動力向量。

為使動力學模型更加切合工程實際， 進一步考慮系統摩擦力及外部干擾后，得到如下形式的機構動力學模型：

(6)

D(t)=umcosωt[111]T

qa=[qa1qa2φ1]T

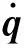
2　動力學控制器設計及神經網絡構建

2.1PD滑模神經網絡動力學控制器設計

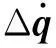
(7)

PD滑模神經網絡控制系統結構如圖3所示，其控制律設計為

τ=τfb+τff+τsm

(8)

式中，Kp、Kd、τ均為對稱正定矩陣；τfb為常規PD反饋控制項；τff為神經網絡控制項；τsm為滑模控制項；εm取神經網絡擬合誤差的上界值，用來增強系統的魯棒性。

圖3　PD滑模神經網絡動力學控制系統結構圖

滑模面設計為

(9)

其中，A可逆，a1、a2、a3均為可調參數并滿足霍爾伍茲條件。

滑模控制取等速趨近率：

(10)

k1,k2,k3>0

下面證明所設計PD滑模神經網絡動力學控制算法的穩定性。

將式(8)代入式(6)并整理可得

(11)

定義Lyapunov函數為

V=STS/2=[s1s2s3][s1s2s3]T/2

(12)

對式(12)求導可得

(13)

定義

(14)

將式(14)代入式(13)得

(15)

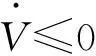
根據Lyapunov穩定性定理，可見基于動力學模型所設計PD滑模神經網絡控制算法穩定。

2.2神經網絡構建

BP神經網絡可以逼近任意非線性映射關系，屬于全局逼近方法，具有較好的泛化能力[17]，故本文采用BP神經網絡實現對混聯機構的前饋控制。構建該神經網絡的步驟如下：

(1)確定BP神經網絡結構。依據所建立的混聯機構動力學模型，確定BP神經網絡輸入量、輸出量分別為混聯機構連接桿中點的位姿向量與混聯機構各主動副驅動力/力矩，因此對應神經網絡輸入層和輸出層均有3個節點。為提高神經網絡精度，在輸入層與輸出層間設計有一個包含16個神經元節點的隱層。

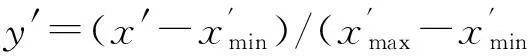
(3)設定BP神經網絡各參數。在訓練BP神經網絡之前，需要設定神經網絡各層的傳遞函數、訓練函數、權值/閾值、學習函數、最大訓練次數、訓練目標誤差等。文中，最大訓練次數設定為30 000，目標誤差設為10-10，其余參數均采用默認設置。

(4)訓練BP神經網絡。完成以上3個步驟以后，采用MATLAB中的train函數對網絡進行訓練，6540次后訓練誤差收斂，其訓練收斂過程如圖4所示。

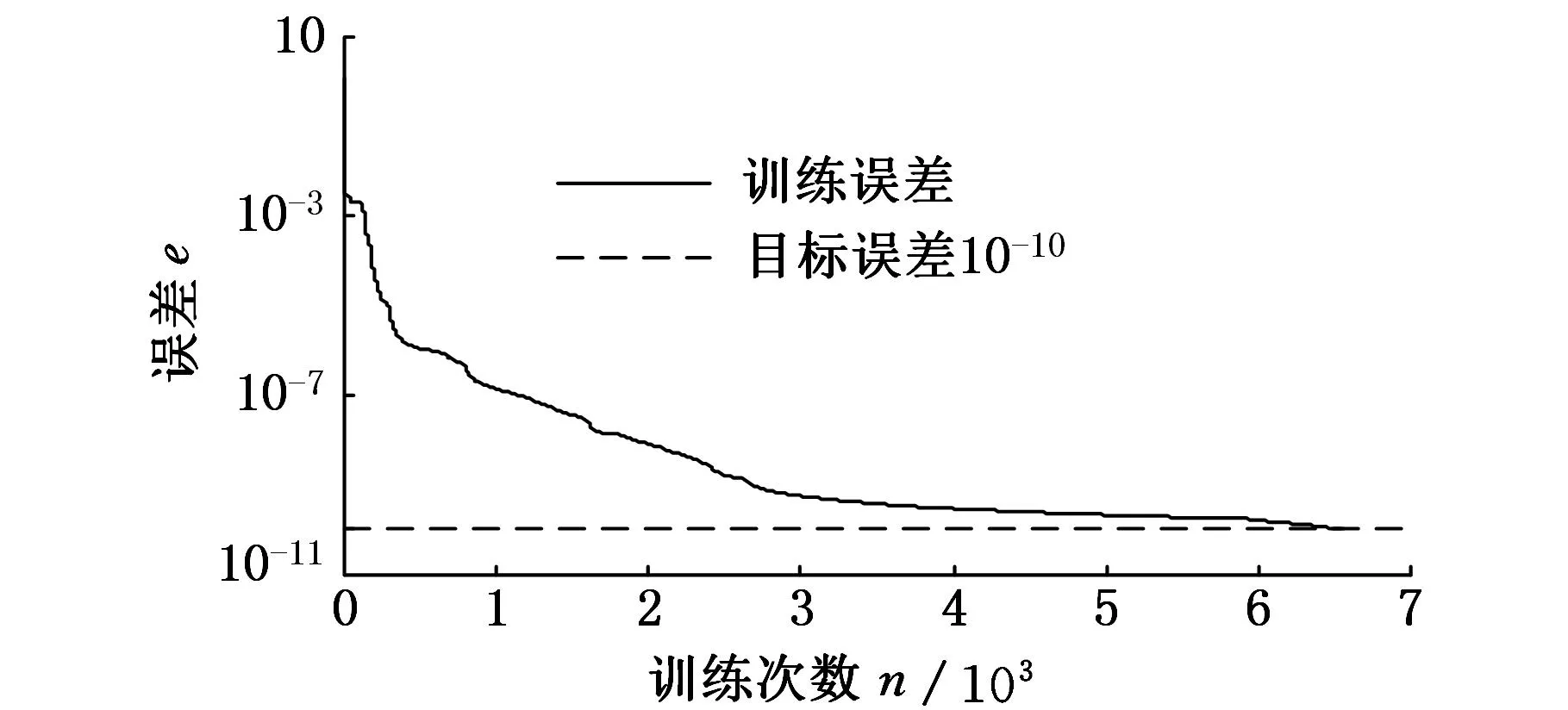
圖4　BP神經網絡訓練收斂過程

訓練后的神經網絡輸入層到隱層權值為

隱層節點與輸出層節點之間的連接權值如表1所示。

表1　隱層節點與輸出層節點之間的連接權值

隱層閾值為

T1=[0.561 30-0.197 42-0.666 95]T

輸出層閾值為

T2=[t1t2…t16]T

t1=7.6352×100t2=-3.3733×100

t3=5.8457×10-1t4=5.7351×100t5=4.5847×100

t6=-5.9803×100t7=4.2038×100

t8=-3.6879×100t9=3.5925×100t10=6.3004×100

t11=-5.4450×100t12=-4.7982×10-2

t13=-5.3814×100t14=6.4484×100

t15=3.4360×100t16=-6.0158×100

神經網絡隱含層神經元的傳遞函數采用S型函數2/(1+e-2x)-1，輸出層神經元采用線性函數。

3　仿真實驗及結果分析

根據1.2節建立的混聯機構(參數如表2所示)動力學模型(式(6))，采用MATLAB進行仿真。由于本文控制方法含有滑模控制作用，可提高系統對外部干擾及參數變化的魯棒性，因此根據文獻[15]，可確定黏度系數矩陣Bc=diag(0.6,0.6,0.9)(N·m)，庫侖摩擦力矩陣Fc=diag(3.7，3.7，4.3)(N·m)，根據文獻[16]，可確定um=0.04，ω=3。

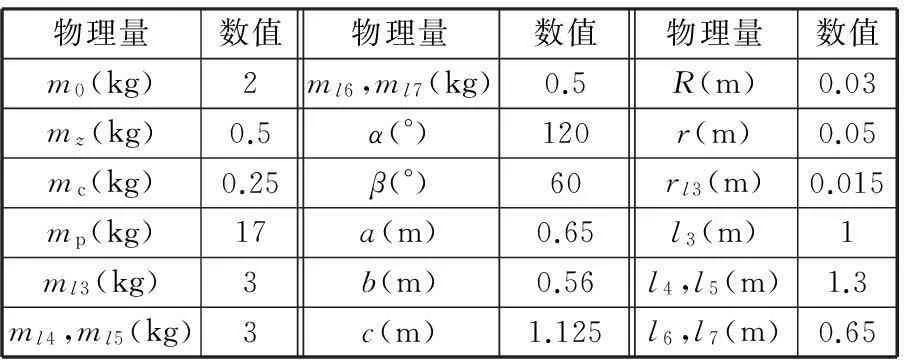
表2　混聯機構參數

根據汽車電泳涂裝工藝要求，輸送設備需輸送白車身完成先翻轉入槽、再在槽中作小幅正弦運動、最后翻轉出槽的運動過程，據此確定升降翻轉機構連接桿中點的期望運動軌跡：

qd=[x(t)z(t)β(t)]T

(16)

x(t)=0.1t0≤t≤9

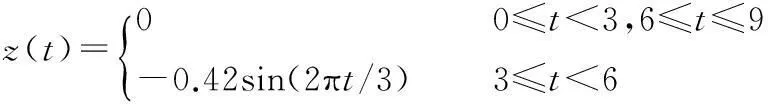
(17)

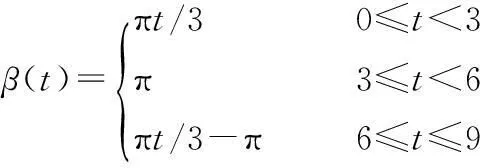
(18)

式中，t為時間，s。

對于圖3所示動力學控制系統，為了驗證引入BP神經網絡對提高系統實時性的有效性，以式(16)～式(18)所示期望運動軌跡為輸入，利用MATLAB中的“tic”、“toc”指令分別測試逆動力學模型從輸入到輸出的計算時間和神經網絡從輸入到輸出的計算時間，結果顯示：前者仿真用時95ms，后者仿真用時49ms。由此可見，與直接采用逆動力學模型控制的方法相比，采用BP神經網絡實現混聯機構前饋控制可有效提高計算效率，從而提高控制系統實時性。

為驗證所設計控制算法的正確性和有效性，以混聯機構的動力學模型(式(6))為被控對象數學模型，分別采用PD滑模控制器(去除圖3中的神經網絡控制項τff)和PD滑模神經網絡控制器(式(8))，對系統跟蹤期望運動軌跡的跟蹤控制過程進行了仿真實驗。兩種控制器的性能通過仿真調試達到最優，確定PD滑模控制器中的參數：

Kd1=diag(10 030，10 030，15 320)

Kp1=diag(904 050，904 050，1 017 020)

εm1=0.1

PD滑模神經網絡控制器中的參數：

Kd2=diag(15 000，12 000，19 000)

Kp2=diag(100 000，807 500，1 000 000)

εm2=0.0099

圖5所示為PD滑模控制器和PD滑模神經網絡控制器作用下，混聯機構連接桿中點位姿各分量的軌跡跟蹤曲線。

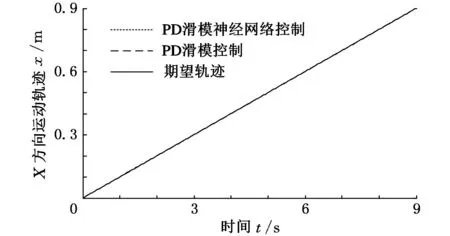
(a)x方向跟蹤曲線

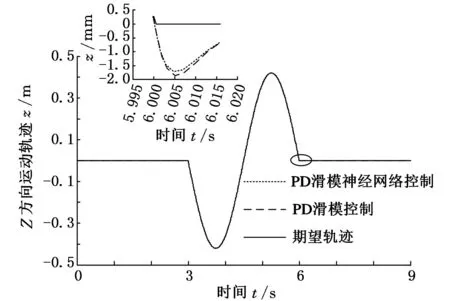
(b)z方向跟蹤曲線

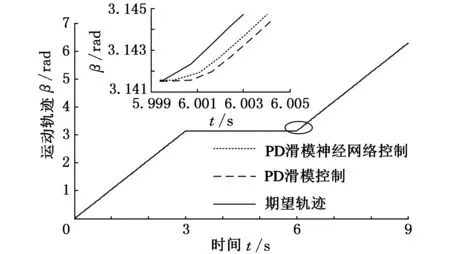
(c)β跟蹤曲線圖5　混聯機構連接桿中點位姿分量軌跡跟蹤曲線

由圖5可見，PD滑模控制器與PD滑模神經網絡控制器作用下，混聯機構連接桿中點位姿的軌跡跟蹤性能差異并不明顯，這是因為二者通過仿真已調試到最優性能。

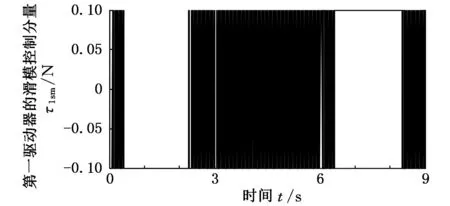
(a)第一驅動器

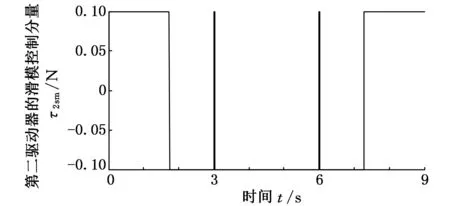
(b)第二驅動器

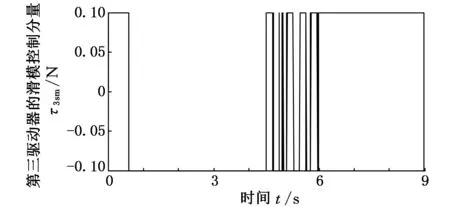
(c)第三驅動器圖6　PD滑模控制器作用下的滑模控制分量曲線

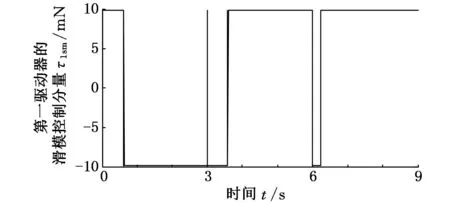
(a)第一驅動器

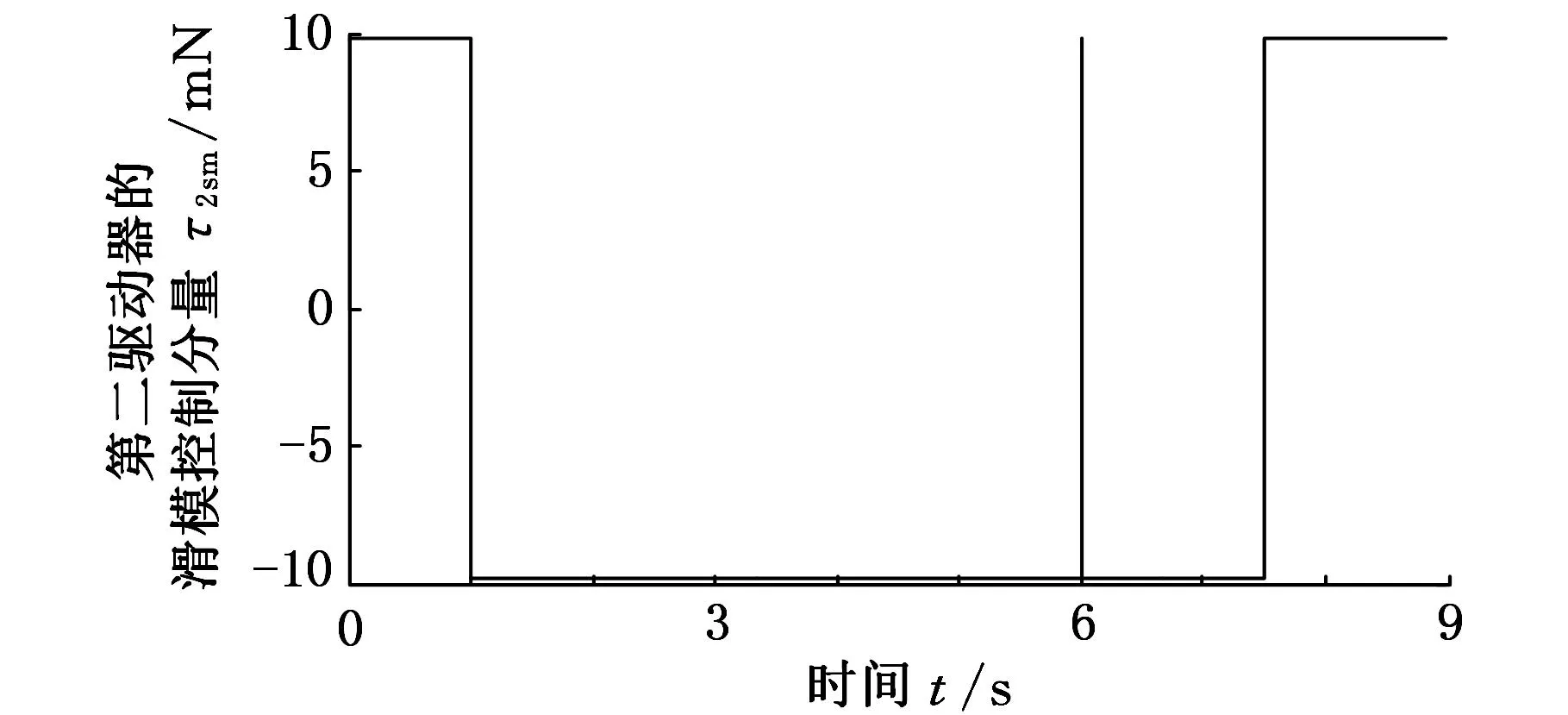
(b)第二驅動器

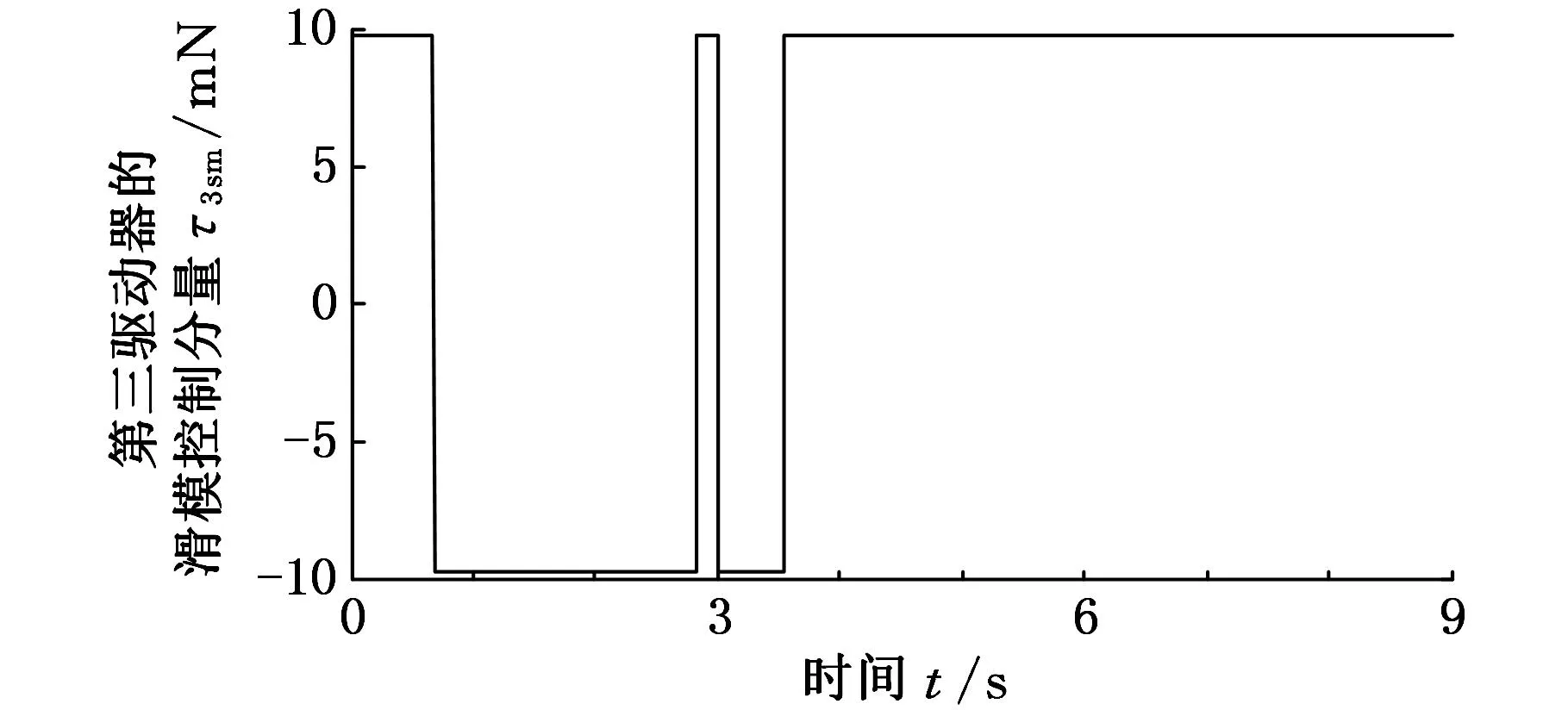
(c)第三驅動器圖7　PD滑模神經網絡控制器作用下的滑模控制分量曲線

圖6為在PD滑模控制器作用下的滑模控制分量曲線圖，圖7為在PD滑模神經網絡控制器作用下的滑模控制分量曲線圖。比較圖6、圖7可以看出，采用PD滑模控制器時，各主動關節驅動力/力矩的滑模控制分量明顯大于采用PD滑模神經網絡控制器時各主動關節驅動力/力矩的滑模控制分量，且控制分量抖振的幅度和頻度均明顯較強，第一驅動器的滑模控制分量抖振較為嚴重，這與期望運動軌跡有關，且由混聯機構的動力學特性決定。由此可見，對于汽車電泳涂裝輸送實際工程系統來說，采用PD滑模控制器時，其滑模控制分量的抖振幅度較大、頻度較高，因此容易磨損執行機構，縮短執行機構壽命，并難以獲得預期控制性能。與此對比，本文所提出的PD滑模神經網絡控制器，由于具有神經網絡的逆動力學前饋控制，無需PD滑模控制擔負全部的控制任務，因此其滑模控制分量無需以較大的切換增益保證滑模運動的存在及其魯棒性，從而可有效抑制滑模控制抖振，避免對執行機構的不利影響，并能使控制系統呈現良好的控制性能，更好地實現對汽車電泳涂裝輸送用新型混聯機構的高性能控制。

4　結論

(1)提出一種PD滑模神經網絡動力學控制方法。基于所建立動力學模型，在任務空間內設計了該混聯機構的PD滑模神經網絡控制器，并從理論上證明了所設計控制算法的穩定性。

(2)分別采用PD滑模控制器和PD滑模神經網絡控制器，對系統跟蹤期望運動軌跡的性能進行了仿真對比實驗。實驗結果表明：引入神經網絡前饋控制后，所提出PD滑模神經網絡控制器有效解決了PD滑模控制器存在的劇烈抖振問題，使得新型汽車電泳涂裝輸送控制系統呈現良好的控制性能。

[1]李文剛. 先進的汽車涂裝設備[J]. 汽車工藝與材料, 2012(2): 46-50.

Li Wengang. Advanced Automobile Coating Equipment[J]. Automobile Technology & Material, 2012(2): 46-50.

[2]沈惠平，趙海彬，鄧嘉鳴，等. 基于自由度分配和方位特征集的混聯機器人機型設計方法及應用[J]. 機械工程學報, 2011, 47(23): 56-64.

Shen Huiping，Zhao Haibin，Deng Jiaming，et al. Design Method and Application of Hybrid Robot Model Based on the Distribution of Degrees of Freedom and the Azimuth Feature Set[J]. Journal of Mechanical Engineering, 2011, 47(23): 56-64.

[3]王燕偉. 一種五自由度混聯機器人的運動學分析與仿真[D]. 哈爾濱：哈爾濱工業大學, 2013.

[4]洪振宇, 張志旭, 許致華. 一種新型三自由度混聯機構基于剛度性能的尺度綜合方法[J]. 中國機械工程, 2014, 25(5) : 619-623.

Hong Zhenyu, Zhang Zhixu, Xu Zhihua. Dimensional Synthesis of a Novel 3-DOF Hybrid Manipulator Based on Stiffness[J]. China Mechanical Engineering, 2014, 25(5): 619-623.

[5]劉辛軍, 陳祥, 高國琴. 一種三自由度汽車涂裝輸送機[P]. 中國：CN102817064A, 2012-12-12.

[6]張耀欣, 叢爽. 平面二自由度冗余驅動并聯機構的最優運動控制及其仿真[J]. 系統仿真學報, 2005, 17(10): 143-147.

Zhang Yaoxin, Cong Shuang. The Optimum Motion Control and Simulation of Planar Two-DOF Redundant Actuation Parallel Mechanism[J]. Journal of System Simulation,2005, 17(10): 143-147.

[7]宗朝. 不確定二自由度冗余并聯機器人控制方法研究[D]. 南京：南京理工大學, 2013.

[8]尤晶晶,李成剛,吳洪濤. 基于四面體構型的冗余并聯機構的運動學分析[J]. 中國機械工程, 2013, 24(8): 1097-1101.

You Jingjing, Li Chenggang, Wu Hongtao. The Kinematic Analysis of the Redundant Parallel Mechanism Based on Tetrahedral Configuration[J]. China Mechanical Engineering, 2013, 24(8): 1097-1101.

[9]郝齊. 一種兩自由度并聯機構優化設計及動力學控制研究[D]. 北京：清華大學, 2011.

[10]Yu W S,Weng C C. H-tracking Adaptive Fuzzy Integral Sliding Mode Control for Parallel Manipulators[J]. Fuzzy Sets and Systems, 2014, 248: 1-38.

[11]Hacioglu Y, Arslan Y Z, Yagiz N. MIMO Fuzzy Sliding Mode Controlled Dual Arm Robot in Load Transportation[J]. Journal of the Franklin Institute, 2011, 348(8): 1886-1902.

[12]Le T D, Kang H J. An Adaptive Tracking Controller for Parallel Robotic Manipulators Based on Fully Tuned Radial Basic Function Networks[J]. Neurocomputing, 2014, 137: 12- 23.

[13]敖銀輝. 平面并聯機構的自適應控制方法研究[J]. 中國機械工程, 2010, 21(7): 835-838.

Ao Yinhui. Research on Adaptive Control for a Planar Parallel Mechanism[J]. China Mechanical Engineering, 2010, 21(7): 835-838.

[14]孫增圻, 鄧志東,張再興. 智能控制理論與技術[M]. 北京：清華大學出版社, 2007.

[15]尚偉偉. 平面二自由度并聯機器人的控制策略及其性能研究[D]. 合肥：中國科學技術大學, 2008.

[16]Isidori A. Nonlinear Control System[M]. Berlin: Spring-Verlag, 1995.

[17]李小力, 陳威, 閆蓉. 基于BP神經網絡的空間輪廓誤差自適應補償[J]. 中國機械工程, 2010, 21(16): 1902-1906.

Li Xiaoli, Chen Wei, Yan Rong. Adaptive Compensation of Contour Errors Based on BP Neural Networks[J]. China Mechanical Engineering, 2010, 21(16): 1902-1906.

(編輯張洋)

Dynamics Control of a Novel Hybrid Mechanism for Automobile Electro-coating Conveying

Gao GuoqinFan DujuanFang Zhiming

Jiangsu University，Zhenjiang，Jiangsu，212013

As a novel hybrid mechanism used for automobile electro-coating conveying possessed high nonlinearity and coupling, it was difficult to achieve the high-performance control. To solve this problem, a dynamic model of the hybrid mechanism was established by Lagrange method. Then, a PD sliding mode neural network dynamics controller was designed in the task space and the stability of the controller was proved. Finally, the controller was simulated and compared with the PD sliding mode controller. The results show that the dynamics controller, by the action of feed-forward control of neural network, may solve the severe chattering problem existed in the PD sliding mode controller effectively, and may make the automobile electro-coating conveying system achieve the high control performance.

hybrid mechanism; dynamics model; sliding mode control; neural network control

高國琴，女，1965年生。江蘇大學電氣信息工程學院教授、博士研究生導師。主要研究方向為并聯機構及其裝備的控制。發表論文90余篇。范杜娟，女，1990年生。江蘇大學電氣信息工程學院碩士研究生。方志明，男，1978年生。江蘇大學電氣信息工程學院講師。

2015-02-05

國家自然科學基金資助項目(51375210)；江蘇高校優勢學科建設工程資助項目(蘇政辦發[2014]37號)；鎮江市工業科技支撐計劃資助項目(GY2013062)；鎮江市京口區科技計劃資助項目(jkGY2013002)

TH238

10.3969/j.issn.1004-132X.2016.08.004