ELM在航空發動機氣路部件故障診斷的應用研究

王小雷,　林學森,　楊欣毅

(1.中國人民解放軍91715部隊82分隊,廣東 廣州　510750;2.海軍航空工程學院 飛行器工程系,山東 煙臺　264001)

?

ELM在航空發動機氣路部件故障診斷的應用研究

王小雷1,林學森2,楊欣毅2

(1.中國人民解放軍91715部隊82分隊,廣東 廣州510750;2.海軍航空工程學院 飛行器工程系,山東 煙臺264001)

摘要：針對航空發動機故障呈現復雜性、多樣性、非線性等特點,運用傳統的BP、ELman神經網絡進行發動機氣路部件故障診斷存在網絡訓練參數設置復雜,迭代次數多,訓練速度慢,泛化能力欠缺等問題。為此提出利用極限學習機(Extreme Learning Machine,ELM)法識別渦扇發動機氣路部件故障。該方法通過為輸入權和隱藏層偏置隨機賦值,利用MP逆求解輸出權值。以某型渦扇發動機為對象,進行ELM、 BP、ELman氣路部件故障診斷比較研究,實驗結果驗證了利用ELM識別渦扇發動機氣路部件故障的精確性、快速性、穩定性。

關鍵詞：航空發動機; 氣路部件; 故障診斷; 極限學習機(ELM)

1引言

航空發動機氣路部件故障對飛機影響巨大,在飛行過程中,航空發動機氣路部件一旦發生故障,后果不堪設想,輕則對飛機的飛行性能造成一定的影響,重則有可能機毀人亡,造成重大損失,所以對航空發動機氣路故障診斷一直受到高度重視[1]。

目前,應用比較廣泛的航空發動機氣路部件數據驅動的方法是神經網絡法,而在神經網絡中應用較多的是BP神經網絡和ELman神經網絡。傳統的BP神經網絡和ELman神經網絡等方法構造信度函數矩陣,網絡訓練參數設置復雜,迭代次數多,訓練速度慢,泛化能力欠缺,容易產生局部最優解,存在一定的隨機性和片面性,可信度較差。為了提高發動機氣路部件的安全性能和可靠性能,必須采用先進的技術手段,來預防或者提前檢測航空發動機氣路部件的故障。針對發動機故障多樣性和復雜性等特點,本研究提出了一種基于極限學習機(ELM)[2]的航空發動機氣路部件故障診斷方法,極限學習機據有批處理,不迭代,訓練和測試速度快的特點。

為了驗證ELM的優越性,在本文中將分別利用ELM、BP和ELman三種方法對渦扇發動機氣路部件故障進行診斷,并對診斷結果進行分析。

2ELM的理論分析

誤差反向傳播神經網絡[3](back-propagationneuralnetworks),簡稱BP神經網絡,它是一種反向傳遞并修正誤差的多層映射網,它由輸入層、中間層和輸出層組成,中間層也就是隱層,可以使一層或多層。BP神經網絡的學習過程分為兩部分組成:正向傳播和反向傳播。當正向傳播時,信息從輸入層經隱單元層處理后傳向輸出層,每一層的神經元的狀態只影響下一層神經元的狀態。如果在輸出層得不到希望的輸出,則轉入反向傳播,將誤差信號沿原來的神經元連接通路返回。返回過程中,逐一修改各層神經元連接的權值。這種過程不斷迭代,最后使誤差信號達到允許的范圍之內。

ELman神經網絡[4]是一種典型的局部回歸網絡(globalfeedforwardlocalrecurrent),ELman神經網絡一般分為四層:輸入層、中間層(隱含層)、承接層和輸出層,,其輸入層、隱含層和輸出層的連接類似于前饋網絡,輸入層的單元僅起信號傳輸作用,輸出層單元起線性加權作用,隱含層單元的傳遞函數可采用線性或非線性函數,承接層又稱為上下文層或狀態層,用來記憶隱含層單元前一時刻的輸出值,可以認為是一個反饋。

在極限學習機(ELM)中,輸入權值和隱含層偏差被隨機初始化給定,輸出權值矩陣利用廣義逆(MP)計算得到。相比傳統前饋神經網絡,ELM學習速度更快、精度更高、參數調整簡單,已經得到不少學者的關注研究,但在實際應用過程中,為了達到理想的誤差精度,ELM通常需要大量的隱含層節點。

(1)

式中:L為隱層節點個數;wj=[ωj1,ωj2,…,ωjn]T為連接第j個隱層節點和輸入節點的權重向量;β=[βj1,βj1,…,βjm]T為連接第j個隱層節點和輸出節點的權重向量;bj是第j個隱層節點的偏置。式(1)可簡寫為

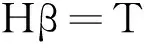
(2)

(3)

式中:H是隱含層神經輸出矩陣,H的第i列是關于輸入x1,x2,…,xn的第i個神經元的輸出。由于隱層輸入權值和閾值不需要調整可以任意賦值,當給定ωi和bi后,訓練單隱藏層前饋神經網絡就等于求線性系統Hβ=T的最小二乘解β=H+T=(HTH)-1HTH,這里H+表示隱含層輸出矩陣{(xi,ti)|xi∈Rm,i=1,2,…,N}的MoorPenrose廣義逆。

ELM的學習算法為:給定一個訓練樣{(xi,ti)|xi∈Rm,i=1,2,…,N},激活函數g(x),隱層神經元L,具體步驟如下:

步驟一:隨機設定隱層的權值ωi和閾值bi,i=1,2,…,L。

步驟二:計算隱層輸出矩陣H。

步驟三:計算隱層矩陣H的逆矩陣。

步驟四:計算輸出層權值β:

(4)

其中:T=[t1,t2,…,tN]T。

3航空發動機氣路故障診斷

3.1渦扇發動機氣路部件故障診斷原理[5]

航空發動機氣路部件主要分為:低壓壓器機、高壓壓氣機、燃燒室、高壓渦輪、低壓渦輪和尾噴管等。

在這些部件之上,可以測量的參數有:低壓壓氣機轉速(低壓渦輪轉速)、高壓壓氣機轉速(高壓渦輪轉速)、高壓壓氣機后壓力、低壓渦輪后壓力、高壓壓氣機后溫度、低壓渦輪出口溫度、尾噴管出口溫度、耗油量等。一般將這些參數作為標致航空發動機是否正常的重要參數,在正常工作的情況下,這些參數都是穩定在一定的值之內的,當這些參數超出正常工作的參數范圍時,則表明該部件出現故障,如圖1所示。

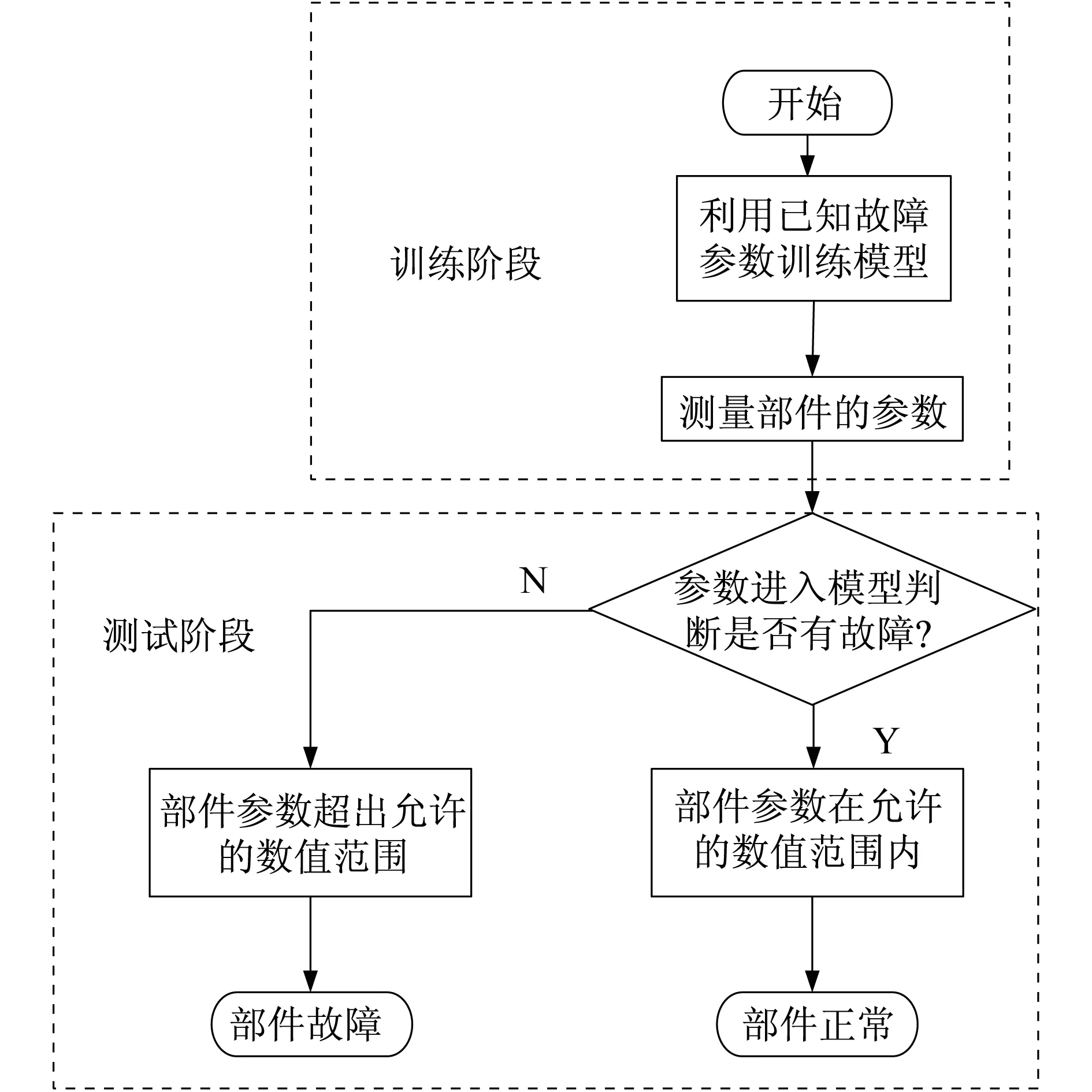
圖1　故障判斷原理Fig.1　Diagram of fault decision

3.2渦扇發動機氣路部件故障診斷

為了研究采用極限學習機(ELM)判斷航空發動機氣路部件故障,本文將ELM與BP神經網絡和ELman神經網絡進行比較,并驗證極限學習機在航空發動機氣路部件故障診斷中的優勢,利用航空發動機氣路部件模擬軟件GSP[6],選擇渦扇發動機氣路部件模型,選取10個指標作為數據測量點,如表1所示。

表1　測量的參數Tab.1　Measurement Parameters

在測量這10個指標時,選擇衰減步長為-0.001,衰減范圍為[-0.001,-0.05],分別生成風扇(低壓壓氣機)的流量衰減數據50組,效率衰減數據50組,壓比衰減數據50組;高壓壓氣機的流量衰減數據50組,效率衰減數據50組,壓比衰減數據50組;高壓渦輪的流量衰減數據50組,效率衰減數據50組;低壓渦輪的流量衰減數據50組,效率衰減數據50組,總共生成500組衰減數據,也就是得到500組有衰減的情況下,這10個指標的測量數據。然后,生成一組在沒有衰減情況下,這10個指標的測量數據,也就是得到10個正常的的測量數據,與之前的500組衰減數據共同構成501組訓練數據。

將測量所得到的每一項數據進行歸一化處理,如高壓壓氣機轉速NH,用高壓壓氣機測量轉速減去高壓壓氣機最小轉速所得的絕對值,除以高壓壓氣機最大轉速減去高壓壓氣機最小轉速,即

(5)

同理,分別對低壓壓氣機轉速NL,高壓壓氣機后壓力P3,低壓渦輪后壓力P6,高壓壓氣機后溫度T3,低壓渦輪出口溫度T6,尾噴管出口溫度T8,尾噴管出口壓力P8,發動機推力FN和耗油量Tsfc進行歸一化處理。

經過歸一化處理后得到一個501組這10個指標的數據,即歸一化后500組衰減數據,1組正常數據,將前500組數據中,同一種測量指標中采用的相同衰減方式的標上同一個序號,依次標上1,2,3,4,5,6,7,8,9,10,作為訓練數據。

通過實驗驗證得到ELM的測試精度與隱含層節點[7]的關系如圖2所示。

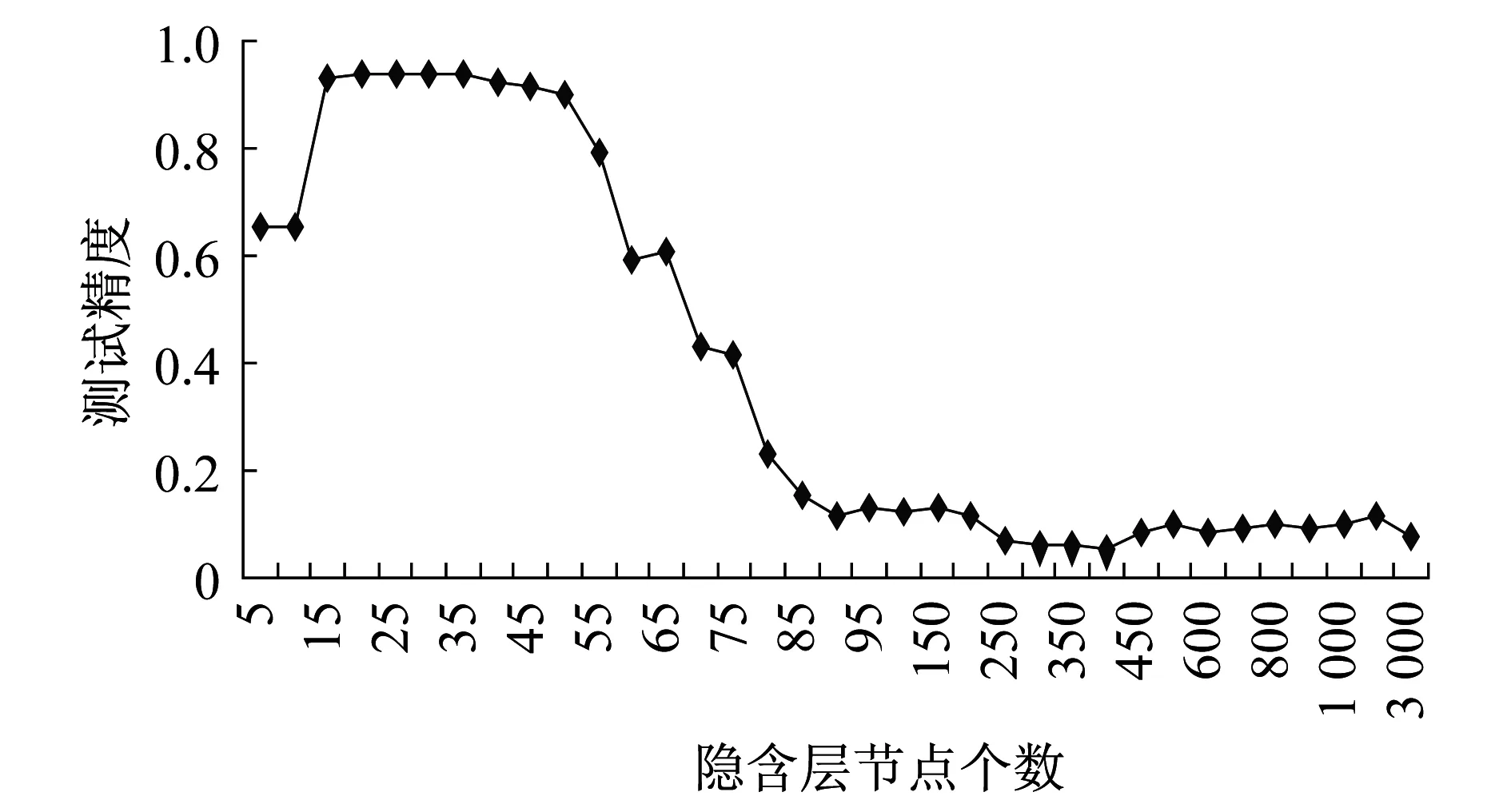
圖2　ELM的測試精度與隱含層節點的關系Fig.2　Testing accuracy varies with the number of ELM hidden nodes

分析可知當隱含層節點為35時,測試精度最高為94.03%,所以在故障診斷中選取ELM的隱含層節點為35個。

該數據均在MatlabR2013a環境下運行的,運行電腦處理器為AMDA6-3420MAPU,1.5GHz,內存為4.00GB,64位操作系統。

利用501組訓練數據分別對ELM、BP和ELman進行訓練,然后對50組測試數據進行測試,分別訓練和測試20次,得到結果如圖3所示。

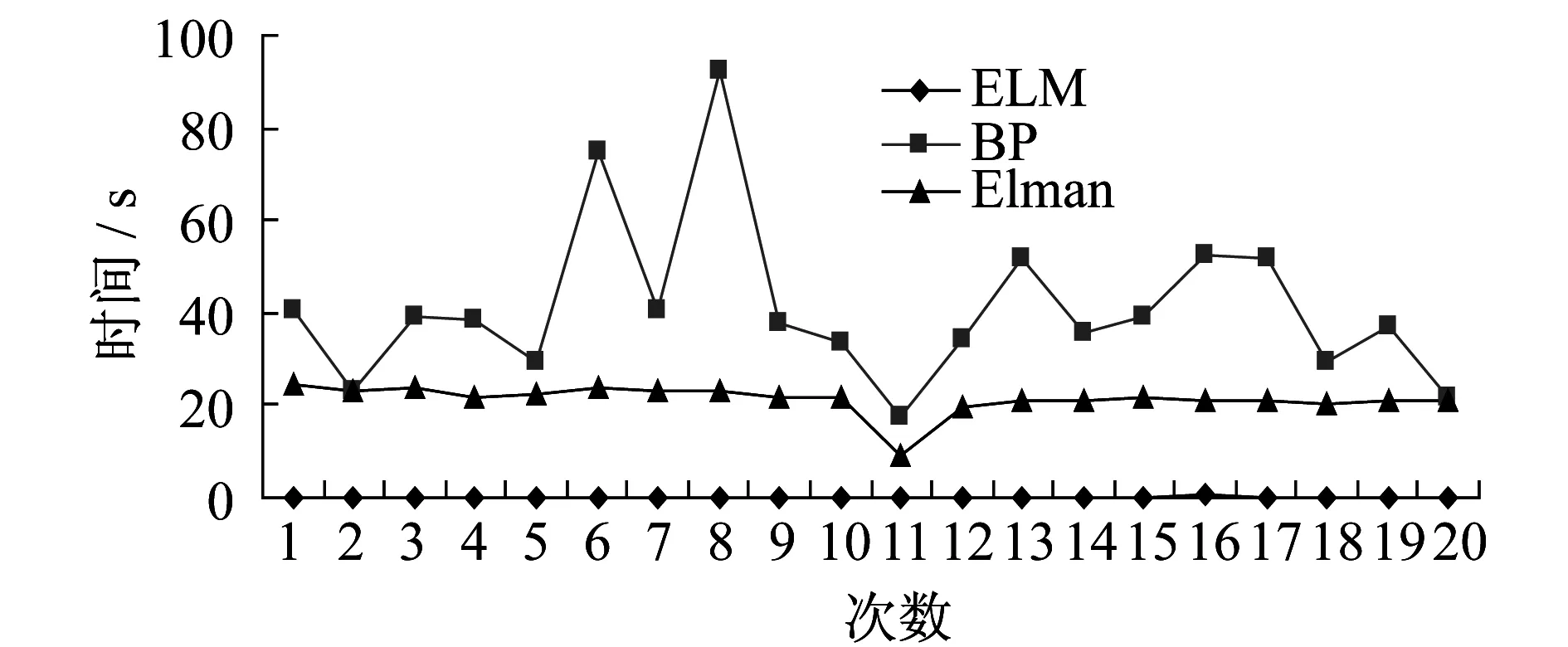
圖3　訓練時間比較圖Fig.3　Comparison of training time

由圖3分析可知,ELM的訓練時間最短,且訓練時間波動最小,為[0.000 0,0.405 6],BP的訓練時間最長,訓練時間的波動最大為[17.752 9,92.227 8],ELman的訓練時間和波動在兩者之間,波動范圍為[9.188 5,24.320 6]。

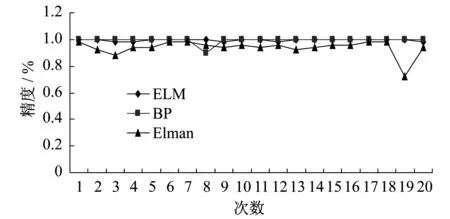
圖4　測試精度比較圖Fig.4　Comparison of training testing accuracy

由圖4分析可知,ELM,BP,ELman這三種方法的測試精度非常接近,其中ELM和BP的測試精度最高,且最穩定,波動范圍為[0.980 0,1.000 0]和[0.900 0,1.000 0],而ELman的波動范圍最大,為[0.720 0,0.980 0]。

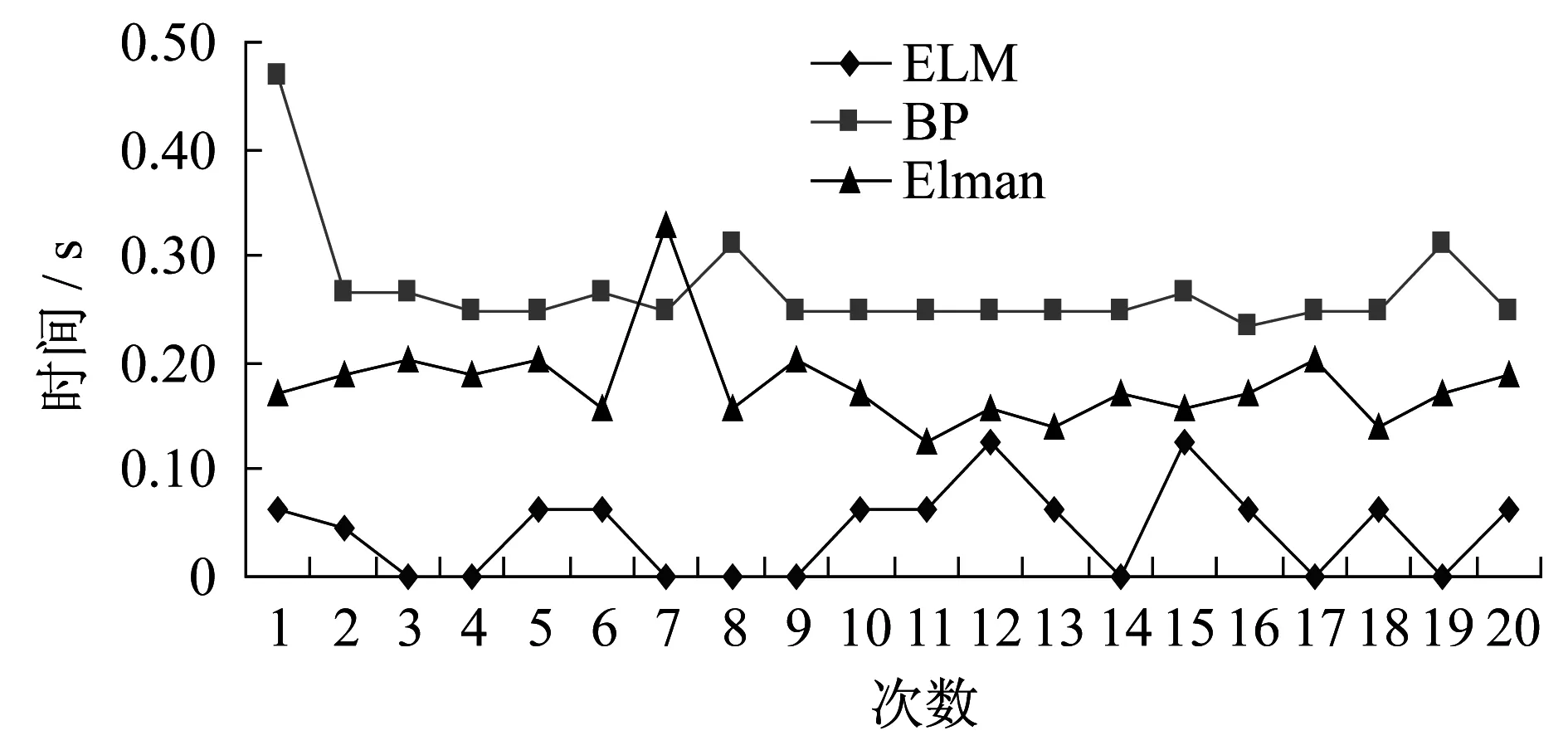
圖5　測試時間比較圖Fig.5　Comparison of training testing time

由圖5分析可以明顯發現,ELM的測試時間最短,波動最小,為[0.000 0,0.124 8],其次是ELman的測試時間較短,波動為[0.124 8,0.327 6],BP的測試時間最長,波動最大,為[0.234 0,0.468 0]。

將501組訓練數據和50組測試數據分別用ELM,BP,ELman這三種方法進行訓練和測試,且采用三種方法各分別訓練和測試20次,得到訓練時間、測試精度和測試時間如表2所示。

分析可知,ELM的訓練時間最短,平均訓練時間為0.099 8秒,且訓練時間波動最小,訓練時間方差為0.007 0;BP的訓練時間最長,訓練時間為ELM的411倍,訓練時間的波動最大,方差為ELM的41390倍;ELman的訓練時間和波動在兩者之間,訓練時間為ELM的212倍,方差為ELM的1 333倍。由此可得,ELM的訓練時間最短且最穩定。

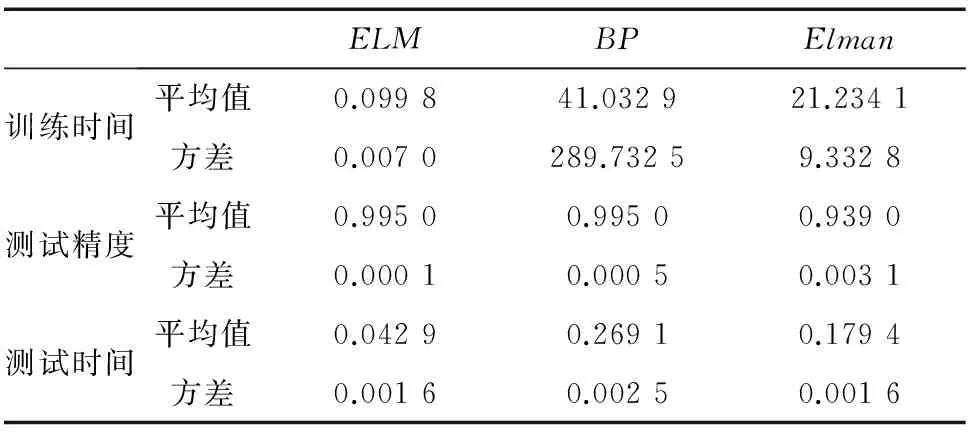
表2　ELM、BP和ELman三種方法比較Tab.2　Performance comparison of ELM,BP and ELman

ELM,BP,ELman這三種方法的測試精度非常接近,其中BP和ELM的測試精度最高,且最穩定。

分析可以發現,ELM的測試時間最短,平均測試時間為0.042 9秒,測試時間方差為0.001 6;其次是ELman的測試時間較短0.179 4,為ELM的4倍,測試時間方差為0.001 6,與ELM相同;BP的測試時間最長,為0.269 1秒,為ELM的6倍,測試時間方差為0.002 5,為ELM的1.56倍。綜合可知ELM的測試時間最短且最穩定。

4結論

通過應用極限學習機對渦扇發動機氣路部件的故障診斷,并與應用BP和ELman進行渦扇發動機氣路部件故障診斷進行比較,得出以下結論:

(1) 運用ELM法進行故障訓練時,能夠在保持方差低于BP和ELman的前提下,大大縮短訓練時間,平均訓練時間為BP的平均訓練時間的1/411,為ELman的平均訓練時間的1/212,有利于進行大數據訓練時提高精度并減少時間。

(2) 運用ELM法進行故障診斷測試時,在保持比ELman精度高,與BP精度幾乎一樣的前提下,測試時間大大縮短了,為BP的1/6,為ELman的1/4,有利于在進行大數據故障測試時節約大量時間,且能夠保持穩定的精度。

(3) 運用ELM法進行故障測試時,與BP、ELman比較,多次測試所得的方差,即訓練時間方差、測試精度方差和測試時間方差均是最小,模型的穩定性最好。

參考文獻:

[1]李應紅,尉詢楷.航空發動機的智能診斷、建模與預測方法[M].北京:科學出版社,2013.

LIYinghong,WEIXunkai.Intelligentdiagnosis,modelingandpredicationmethodforaeroengine[M].Beijing:SciencePress,2013.

[2]HUANGGuangbin,ZHUQinyu,SiewCheekheong.Extremelearningmachine:theoryandapplications[J].Neurocomputing,2006,70(1/2/3):489- 501.

[3]田雨波.混合神經網絡技術[M].北京:科學出版社,2009.

TIANYubo.Technologyonmixneuralnetwork[M].Beijing:SciencePress,2009.

[4]任麗娜.基于Elman神經網絡的中期電力負荷預測模型研究[D].蘭州理工大學,2007.

RENLina.MiddletermelectricpowerloadpredictionbasedonElmanneuralnetwork[D].Lanzhouuniversityofscienceandengineering,2007.

[5]范作民,孫春林,白杰.航空發動機故障診斷導論[M].北京:科學出版社,2004.

FANZuoming,SUNChunlin,Baijie.Introductiontoaeroenginefaultdiagnosis[M].Beijing:SciencePress,2004.[6]VisserWPJ,KogenhopO.Aqenerieapproachforgasturbineadaptivemodeling,[R],NLR-TP-2004-391.

[7]張德豐.MATLAB神經網絡應用設計[M].北京:機械工業出版社,2011.

ZHANGDefeng.ApplicationsanddesignofNeuralnetworkusingMatlab[M].Beijing:MechanicalIndustryPress,2011.

王小雷男(1989-),湖南萊陽人,學士,主要研究方向為發動機維修與故障診斷。

林學森男(1990-),山東濰坊人,博士研究生,主要研究方向為發動機狀態監控與故障診斷。

中圖分類號：TP 183

文獻標識碼：A

Research on ELM Application in Aeroengine gas Path Components Fault Diagnosis

WANG Xiaolei1,LIN Xuesen2,YANG Yinyi2

(1.ChinaPLA91715Forces,82Unit,Guangzhou510750China;2.NavalAeronauticalEngineeringInstitute,Yantai264001,China)

Abstract：The aeroengine gas path component faults have the characteristics of complexity,diversity and nonlinear.When applied traditional BP and ELman into aeroengine gas path components fault diagnosis,there exist some problems as complex setting of network parameters,multiple iterations,slow training speed and poor generation performance.In order to solve these problems,Extreme Learning Machine(Extreme Learning Machine,ELM)method was used to aeroengine gas path components fault diagnosis.This method randomly assigned input weights and biases and calculate output weights by Moore-penrose,pseudo- inverse.ELM,BP and ELman were studied and compared on a certain type of turbofan engine.The results verify the diagnostic accuracy,quickness and stability of ELM.

Key words：aircraft engine; gas path components; fault diagnosis; extreme learning machine(ELM)