空心彈空氣阻力特性計算與數值仿真

張　浩，聞　泉，王雨時，張志彪

(南京理工大學 機械工程學院，南京　210094)

?

空心彈空氣阻力特性計算與數值仿真

張浩，聞泉，王雨時，張志彪

(南京理工大學 機械工程學院，南京210094)

摘要：應用Fluent軟件仿真空心彈典型設計方案簡化模型的空氣動力流場，得到了其阻力系數與馬赫數的關系，運用Matlab軟件數值求解空心彈外彈道質心運動微分方程組，得到了彈道頂點和落點諸元。將以上所得阻力系數和彈道諸元與公式計算結果進行對比表明：在來流馬赫數為2.0～4.4時，無彈帶結構的簡化空心彈模型用兩種方法所得外彈道諸元結果相差很小；彈丸頭部前緣厚度在可信區間內對阻力系數影響較小，但彈帶結構對阻力系數的影響較大；工程設計時，受彈帶結構影響，某空心彈簡化模型阻力系數計算公式不太適合于工程問題求解，此時應以數值仿真為佳。

關鍵詞：空心彈；仿真；公式；阻力系數；外彈道

本文引用格式：張浩，聞泉，王雨時，等.空心彈空氣阻力特性計算與數值仿真[J].兵器裝備工程學報，2016(7):5-11.

Citation format:ZHANG Hao，WEN Quan，WANG Yu-shi，et al.Theoretical Calculations and Numerical Simulation on Air Resistance Characteristics of Hollow Projectile[J].Journal of Ordnance Equipment Engineering,2016(7):5-11.

空心彈(Hollow Projectile)相對于實心彈而言，屬于超音速旋轉穩定彈藥，其飛行部分最簡單的形式就是一個中空薄壁圓管，因此又稱為管式彈(Tubular Projectile)。空心彈沿彈丸軸線是一通孔，幾乎所有靠近圓管前端面的空氣都從孔中流過，而外表面的空氣理論上保持平行幾乎未受擾動。與實心彈相比，空心彈的頭部激波阻力和尾部渦流阻力大大減小。射擊試驗表明空心彈阻力系數一般可降為普通彈的1/2到1/3。另外，空心彈還具有速度高、飛行時間短、命中精度高以及對目標侵徹能力強等一系列優異特性[1-3]。

從上世紀70年代初以來，世界各國廣泛開展了空心彈的基礎理論研究和應用開發研究，所研究的口徑從5.56 mm一直到105 mm(坦克炮訓練彈)，重點是7.62 mm(槍彈)和20 mm(炮彈)，很多著名的科研機構和軍火商都都在積極參與。我國空心彈技術的研究工作起步于上世紀70年代末，但基本上屬于對國外研究成果的試驗驗證。近年來，隨著計算流體力學的發展，應用流體動力學仿真軟件對空心彈流場進行數值模擬的技術已逐漸成熟。南京理工大學高旭東等[4-5]應用高精度、高分辨率的隱式有限體積TVD格式，結合分區算法，數值模擬了氣流入口收斂面積比不同的空心彈內外流場結構，證實存在使彈丸阻力最小的氣流入口面積比。任登鳳[6]采用非結構網格的LU-S GS隱式算法計算三維Euler方程，數值模擬了不同馬赫數及不同攻角下某空心彈的繞流流場，分析了流場波系結構及其升力和阻力特性。錢吉勝等[7]研究了空心彈在不同馬赫數與攻角條件下的流場結構，表明雖然空心彈表面摩阻增加，但其結構帶來的波阻與壓阻降低使總阻力仍然較小。李艷玲[8-9]、黃振貴[10]等對空心彈的流場結構進行優化，得到了在具有相同內徑、外徑以及彈丸長度條件下阻力系數最小的空心彈幾何結構。

目前，關于流體動力學問題的計算機仿真技術已比較成熟，結果較為可信。但就目前的計算機硬件普及程度，仍嫌效率不足。有必要利用仿真手段驗證以往理論研究成果的適應性和準確性。基于此，本文應用Fluent軟件仿真研究空心彈頭部前緣厚度微小變化以及彈帶對其阻力系數的影響，并結合混合錐形空心彈阻力系數理論計算公式，對比分析數值仿真結果與理論公式計算結果的差異，為空心彈型號產品的設計和開發提供技術基礎。

1空心彈阻力系數計算公式

文獻[11]和文獻[12]根據錐-柱組合體常規彈丸阻力系數計算公式推導了外錐形空心彈和內錐形空心彈阻力系數表達式；文獻[13]進一步給出了混合錐形空心彈的阻力系數計算公式。

混合錐形空心彈簡化模型如圖1所示，其中Di為入口直徑，D0為彈徑，Dt為喉部直徑，θ0為外楔角，θi為內楔角。其阻力系數計算公式為：

(1)

其中

(2)

CDf= 4(1 + 0.15M2)-0.432×

(3)

CDb=(0.633 1-0.332 57M+0.066 19M2-

(4)

式(2)中

式(1)～(4)中L為彈丸全長；Cp為頭部壓阻系數；CDp0、CDp1分別為內、外楔壓阻系數；CDf為摩阻系數；CDb為底部壓阻系數。頭部壓阻系數表達式和摩阻系數表達式均是根據計算流體力學理論推導而來的，而底部壓阻系數表達式是根據105 mm空心彈[14]模型風洞試驗結果擬合得到的。此外，使用該公式時有如下假設前提：

a)兩維流體流動；

b)彈丸攻角為零；

c)附在彈丸前緣上的激波為斜激波。

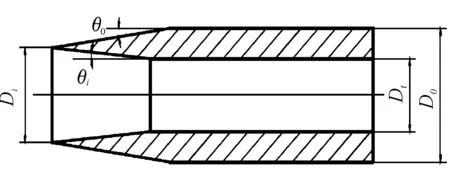
圖1　空心彈結構示意圖

2空心彈流場的數值模擬

2.1數值方法

湍流模型采用常用于航空領域的Spalart-Allmaras單方程模型，運用雷諾平均Navier-Stokes方程對該湍流模型求解，以數值模擬空心彈流場。

雷諾平均Navier-Stokes方程：

(5)

(6)

(7)

使用有限體積法對控制方程進行空間離散，控制節點取網格單元中心。方程的對流項采用混合通量差分(Advection Upstream Splitting Method)格式，而粘性項采用兩階中心差分格式，時間項則取二階R-K格式[8-9]。

2.2彈丸模型及網格

工程實踐中，受工藝等條件的約束，空心彈結構不可能與圖1所示空心彈結構完全相同，圖2為有彈帶的空心彈結構(假設彈帶與彈體一體，并且不考慮身管陽線對彈帶切槽的影響)。以圖2所示空心彈模型為對象，仿真研究空心彈頭部前緣厚度的微小變化以及彈帶對其阻力系數的影響，仿真模型具體結構參數如表1所列，其中模型1與圖1所示空心彈簡化模型完全相同，模型2～模型8增加了彈丸頭部前緣厚度t或增設了彈帶。

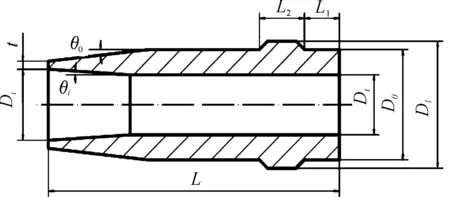
圖2　帶有彈帶的空心彈模型

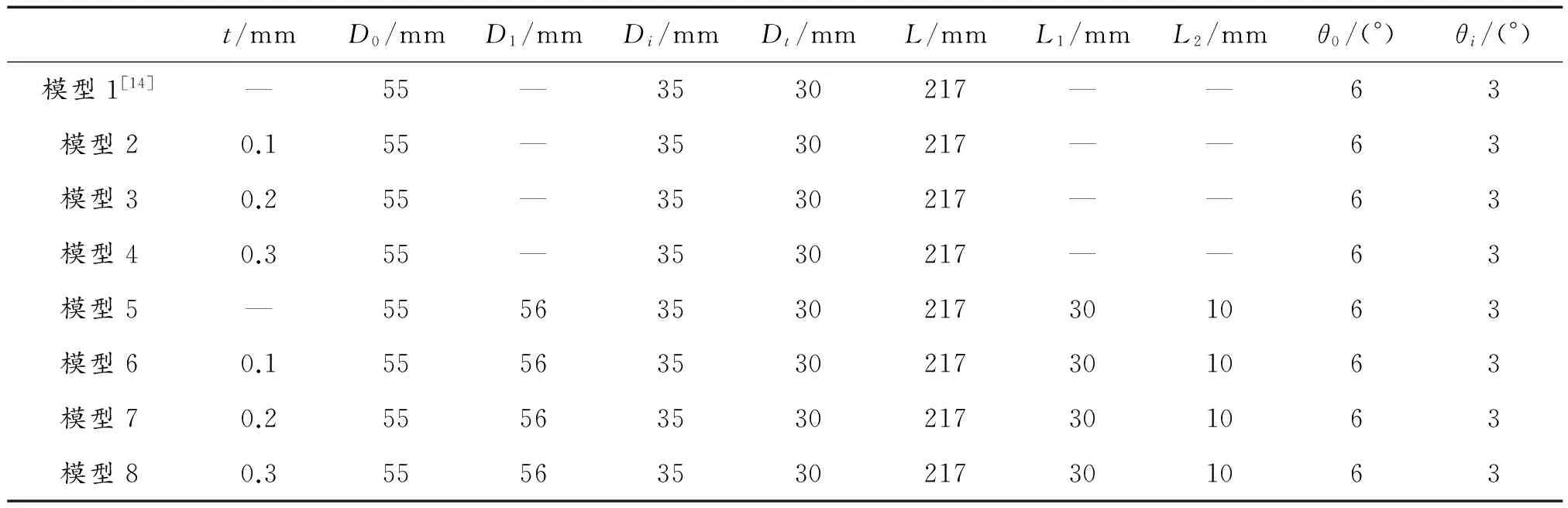
表1　空心彈模型具體參數

使用ANSYS Workbench 14.0中的Fluent模塊建立彈體的仿真簡化模型，取空氣計算域長度為10倍彈長、直徑為20倍彈徑。為了保證計算收斂性和計算結果準確性，采用笛卡爾網格法對計算區域進行網格劃分。笛卡爾網格相對于結構網格、非結構網格具有如下優勢：網格生成簡單，易于實現自動化，具有更強的自適應能力，更適合于處理復雜幾何外形的繞流和由于物體運動或變形等產生的非定常問題。彈丸周圍空氣域網格如圖3所示。

圖3　彈體周圍空氣域網格

設置計算域空氣模型為ideal-gas，選取Sutherland粘度定律。對于邊界條件的設定，取壁面邊界為無滑移絕熱邊界，外邊界取壓力遠場進口與出口邊界，大小為一個標準大氣壓，溫度為300 K，來流馬赫數取為1.2～4.6。選取基于密度的求解器求解。

3結果與討論

3.1流場數值模擬結果與分析

由于篇幅有限，以下只列出馬赫數為1.6、1.8、2.0、4.0時，彈丸(模型1)周圍壓力等值線和速度等值線圖，如圖4～圖11所示。

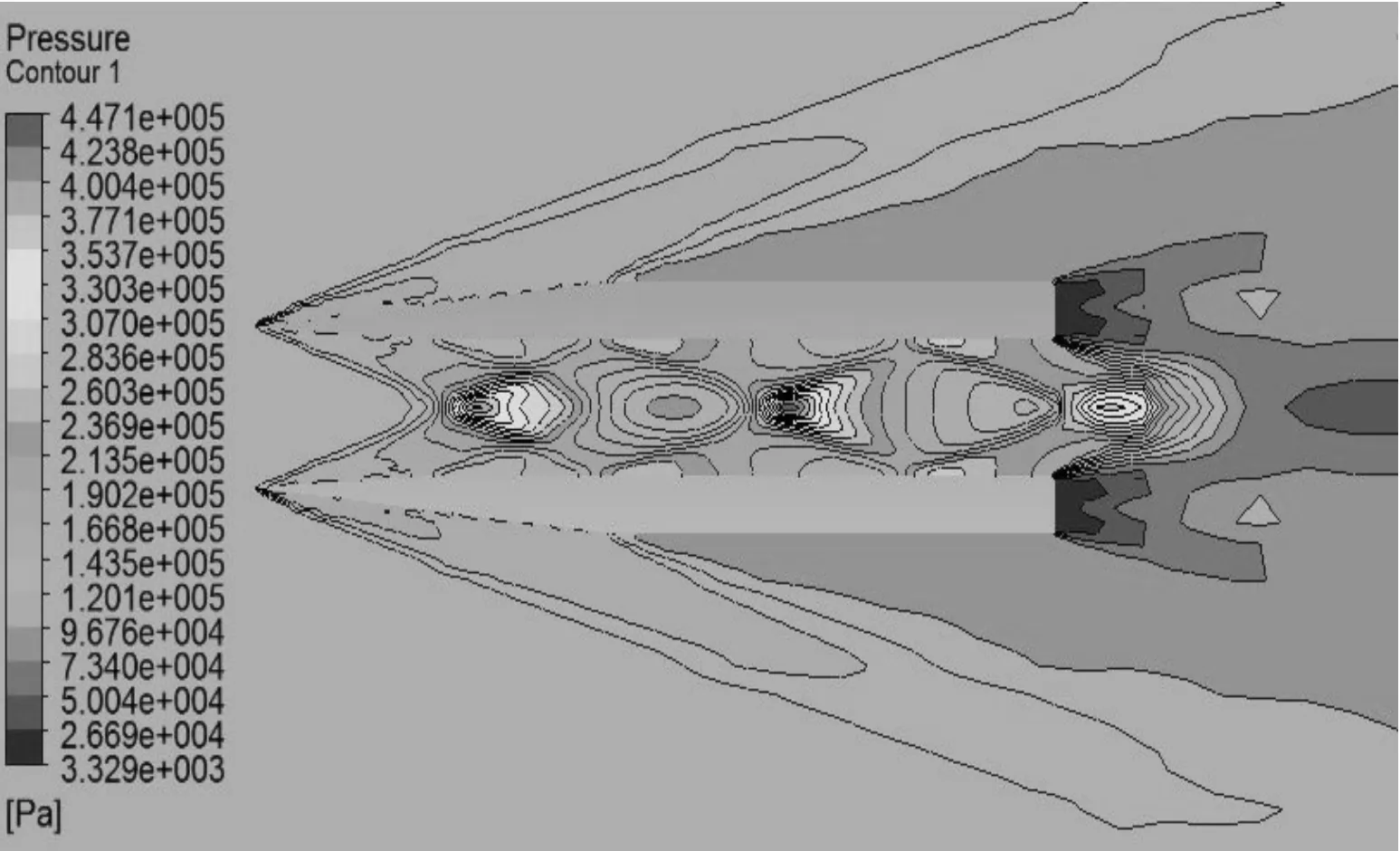
圖4　4.0 Ma時壓力等值線圖

圖5　4.0 Ma時速度等值線圖

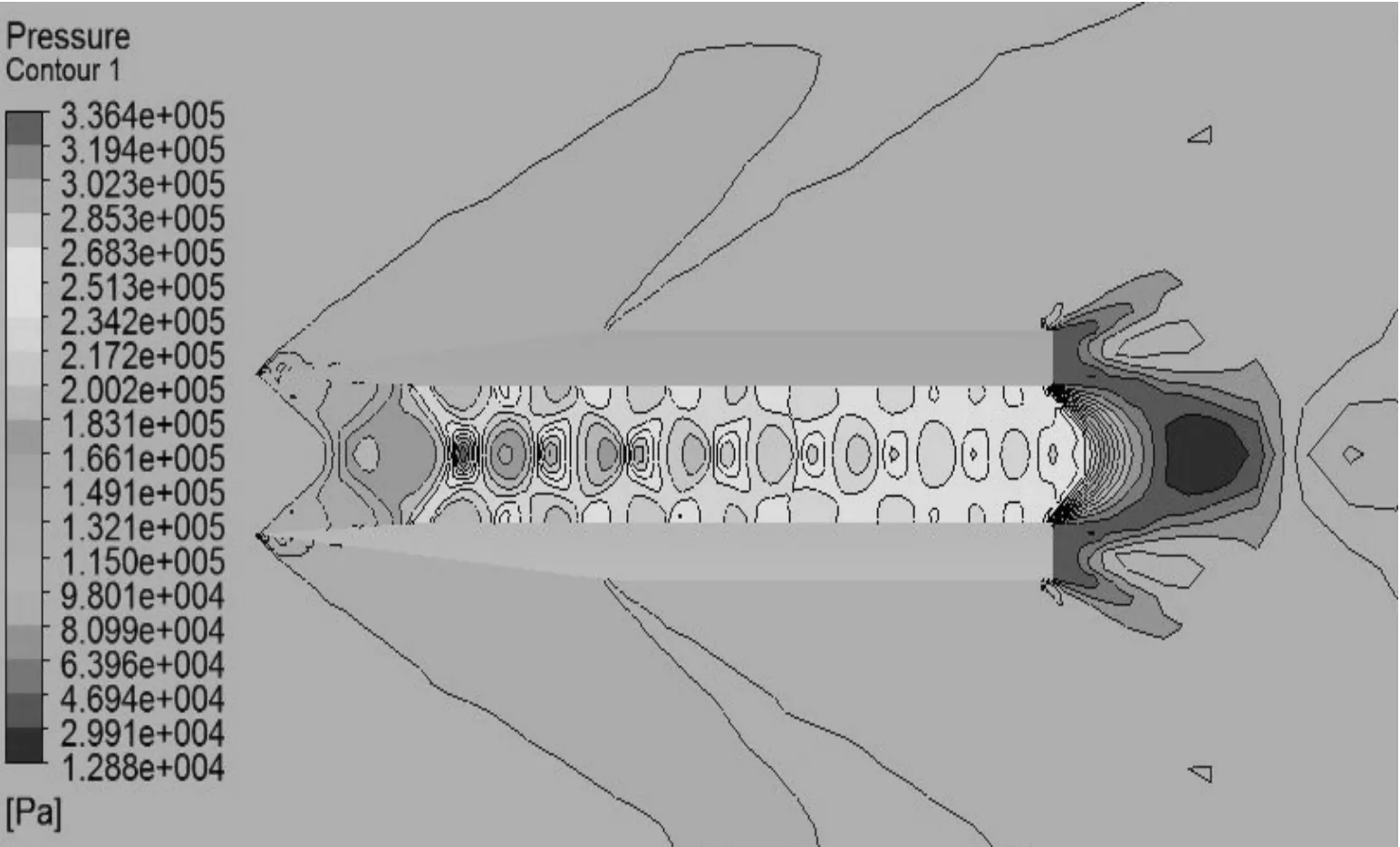
圖6　2.0 Ma時壓力等值線圖

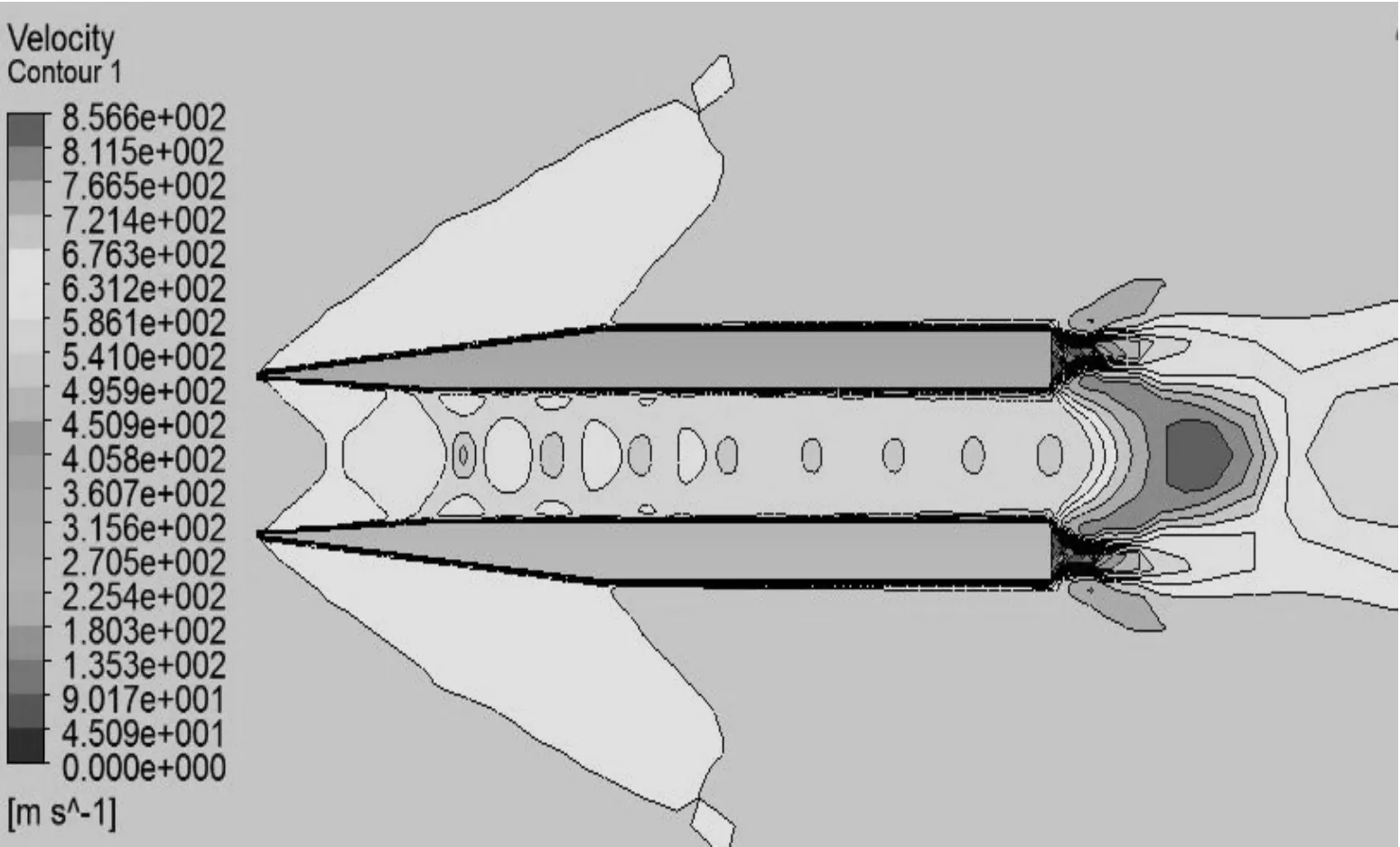
圖7　2.0 Ma時速度等值線圖

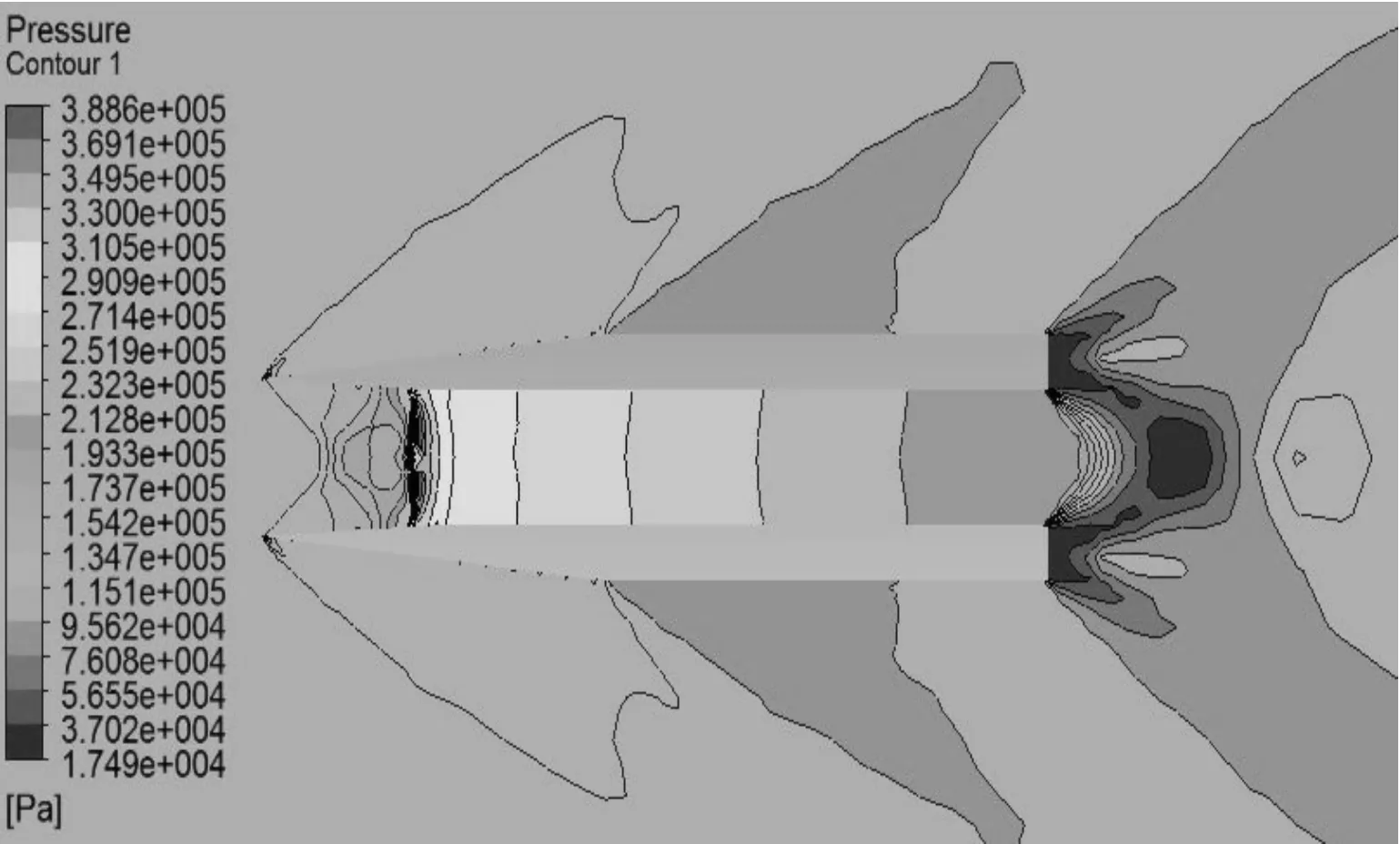
圖8　1.8 Ma時壓力等值線圖

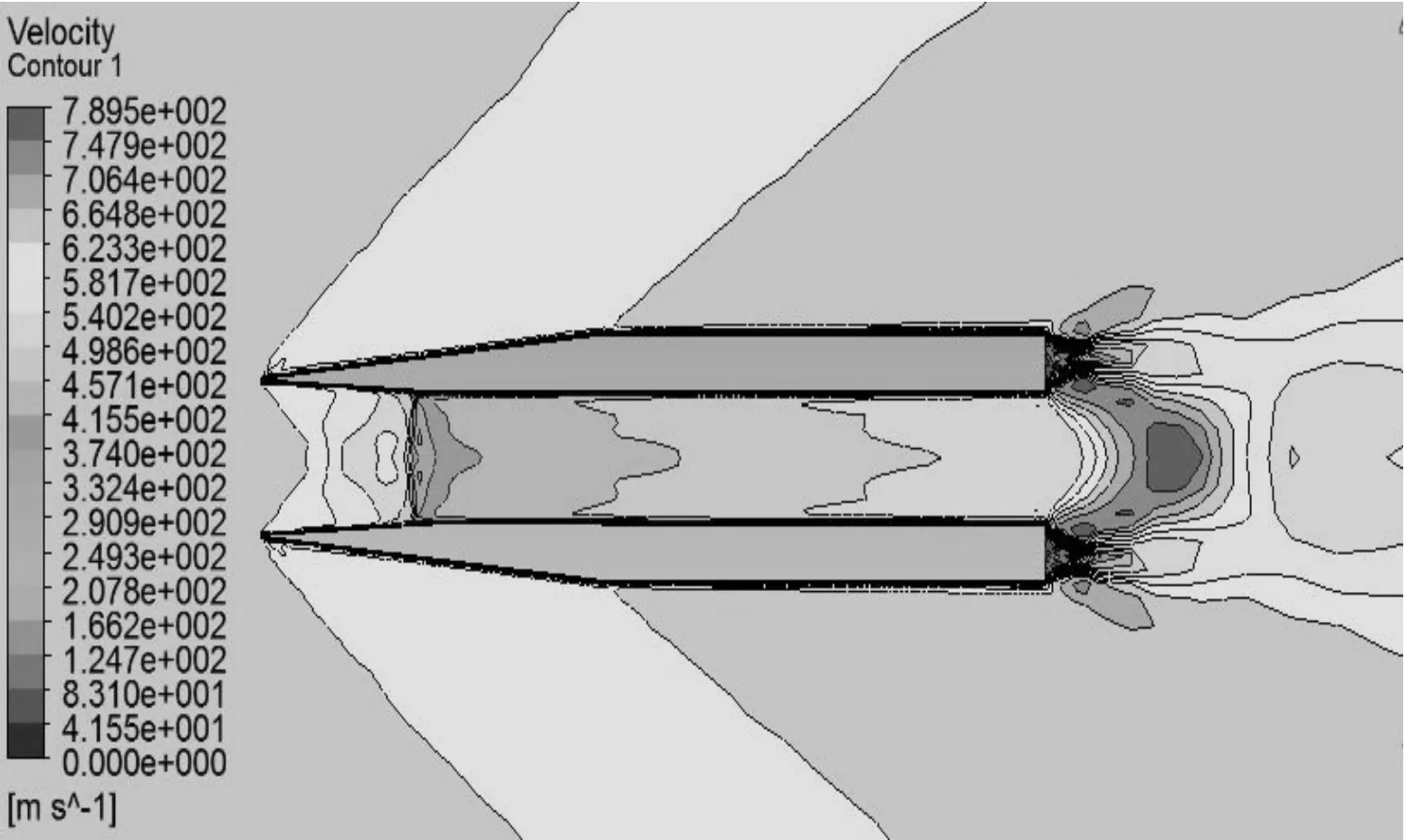
圖9　1.8 Ma時速度等值線圖

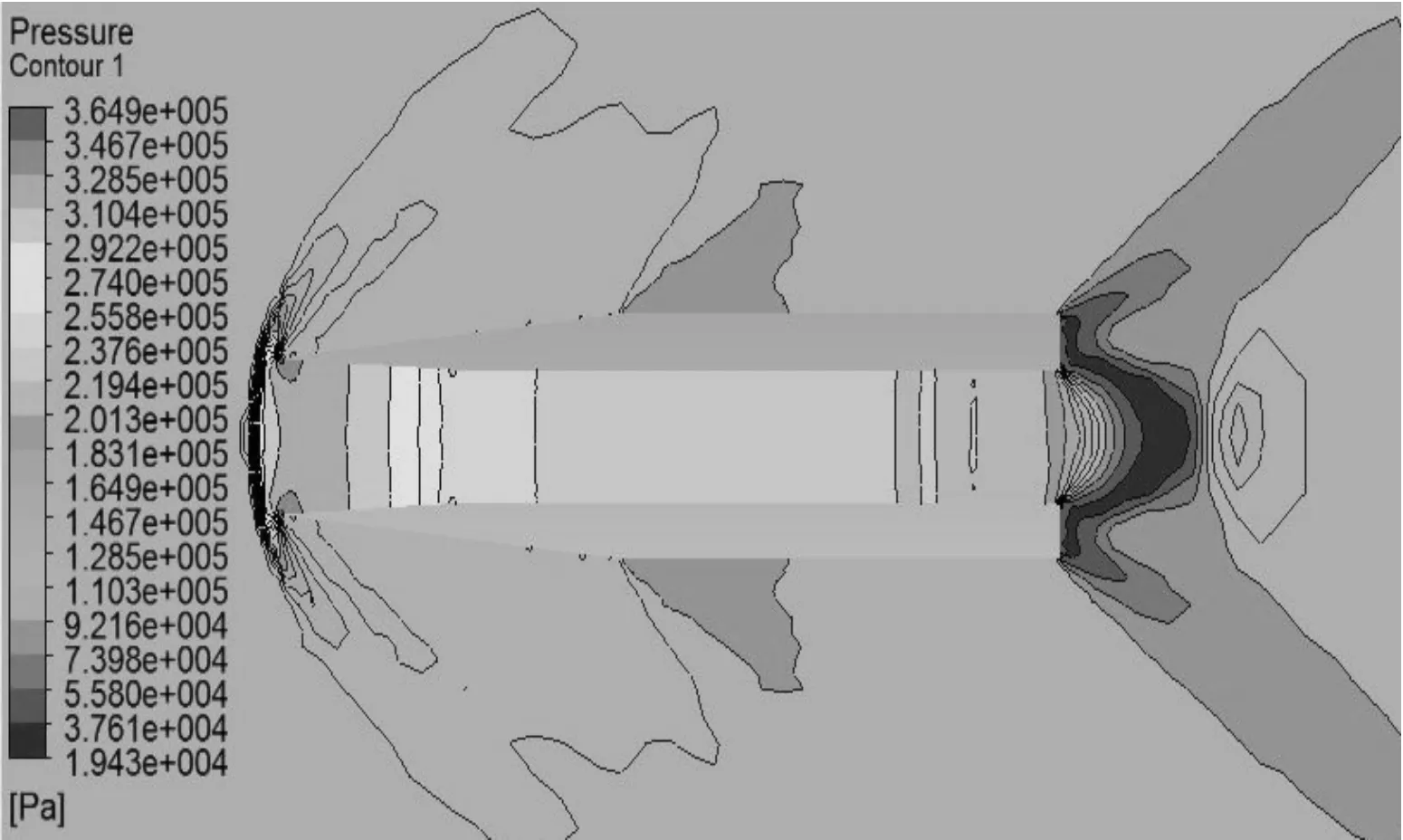
圖10　1.6 Ma時壓力等值線圖

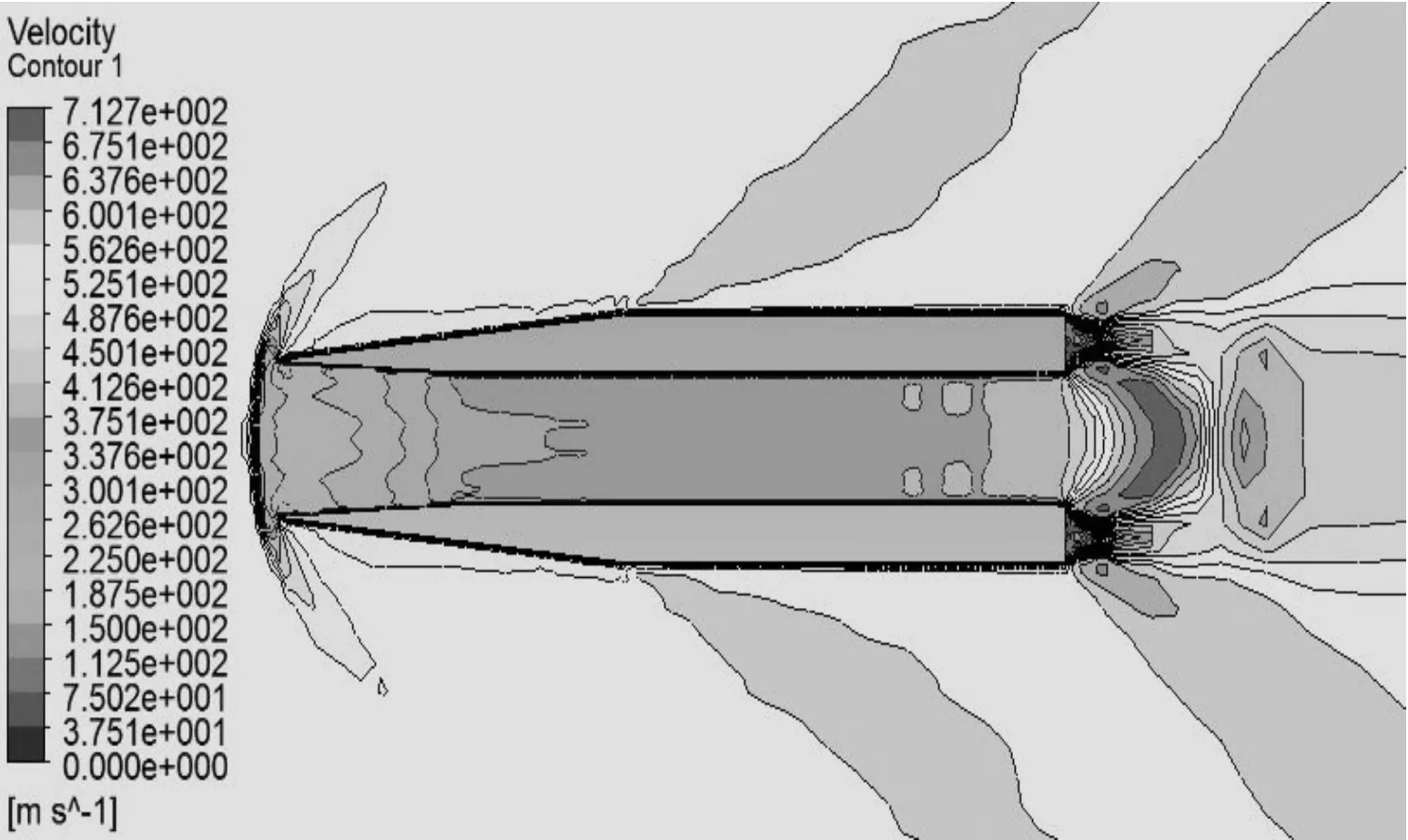
圖11　1.6 Ma時速度等值線圖

對比不同馬赫數下空心彈周圍流場的壓力等值圖和速度等值圖可知：

1) 馬赫數為2.0以上時，空心彈流場波系結構具有相似性，在彈丸的尖頭部分首先產生斜激波。由于彈丸側面無拐角，所以斜激波后形成的壓縮波一直傳遞到彈尾；在空心彈內部，由尖頭部分產生的斜激波流入空心彈內，空心彈內部流動是超音速流動，斜激波在彈丸內壁面反射形成一系列與入射激波相似的反射激波，最后一直延伸到尾部，與彈底膨脹波系相互干擾，彈底壓力急劇減小。激波在彈丸內部交匯從而產生高壓區，隨著馬赫數的降低，斜激波在彈內的交匯點提前了，在彈內壁的反射次數隨之增加。在馬赫數為4.0時，激波在空心彈內壁上的第三次反射落在彈丸內壁尾部；在馬赫數為2.0時，激波在空心彈內壁上形成8次反射。

2) 馬赫數在2.0以下時，如圖8～圖11所示，彈丸頭部不再形成附體斜激波，轉而產生脫體激波，超音速來流經過脫體激波后，氣體將以亞音速流動，彈丸內部發生阻塞，無法形成超音速流動，阻力突然增大。因此，必須消除脫體激波才能減小彈丸所受波阻。

根據仿真結果，彈丸的臨界阻塞速度約為612 m/s(1.8 Ma)，而按文獻[12]給出的空心彈發生“阻塞”的計算公式計算得彈丸的臨界阻塞速度為625.6 m/s(1.84 Ma)，仿真所得阻塞速度與公式計算所得阻塞速度基本一致。

3.2仿真所得阻力系數與文獻[13]所給出的計算公式計算結果對比

表2列出了不同馬赫數條件下仿真與文獻[13]所給出的計算公式所得阻力系數。

由表2可見，來流馬赫數為1.2～4.6時，兩種方法所得摩擦阻力系數相對誤差均在15%以內；來流馬赫數為2.0～4.2時，壓阻系數相對誤差也在15%以內；來流馬赫數Ma在2.0～4.4時間時，總阻力系數的相對誤差小于10%。

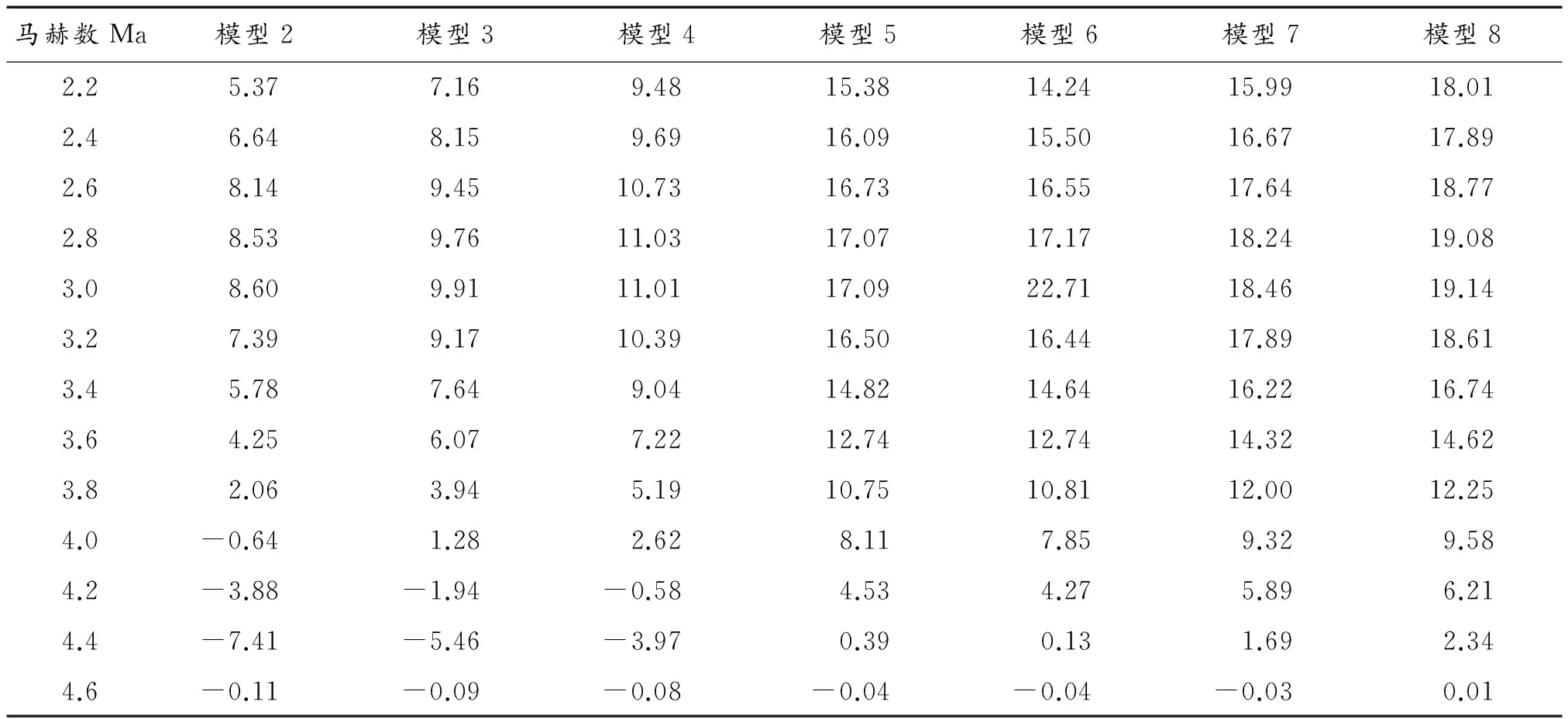
為研究空心彈頭部前緣厚度的微小變化以及彈帶對其阻力系數的影響，將模型2～模型8仿真所得阻力系數與表2中的按文獻[13]所給出的公式計算結果進行對比，計算其相對誤差，如表3所列。

由表3可看出，來流馬赫數為2.0～4.4時，模型2、模型3、模型4總阻力系數的相對誤差小于10%，彈丸頭部前緣厚度對阻力系數影響較小；來流馬赫數小于4.0時，模型5、模型6、模型7總阻力系數的相對誤差大于10%，彈帶對阻力系數的影響較大。

3.3外彈道計算結果與分析

以2.2節空心彈模型1為算例1，以模型8為算例2，以與模型1相似的另一種混合錐形空心彈為算例3。算例3的具體結構參數為：D0=105 mm，Di=98.6 mm，Dt=82.6 mm，L=254 mm，θ0=3°，θi=3.5°。

取彈丸初速為1 292 m/s(3.8 Ma)，另按平均體積和材料密度得出質量數據。采用Matlab軟件分別對仿真所得阻力系數結果與文獻[13]所給出的公式計算結果進行擬合，并建立空心彈質心運動微分方程組。經仿真解算，得到0.5°、1°和2°三種射角下分別用仿真所得阻力系數擬合曲線函數表達式(方法A)和用公式計算所得阻力系數擬合曲線函數表達式(方法B)數值解算空氣質點外彈道得到的頂點諸元和落點諸元和如表3和表4所列。

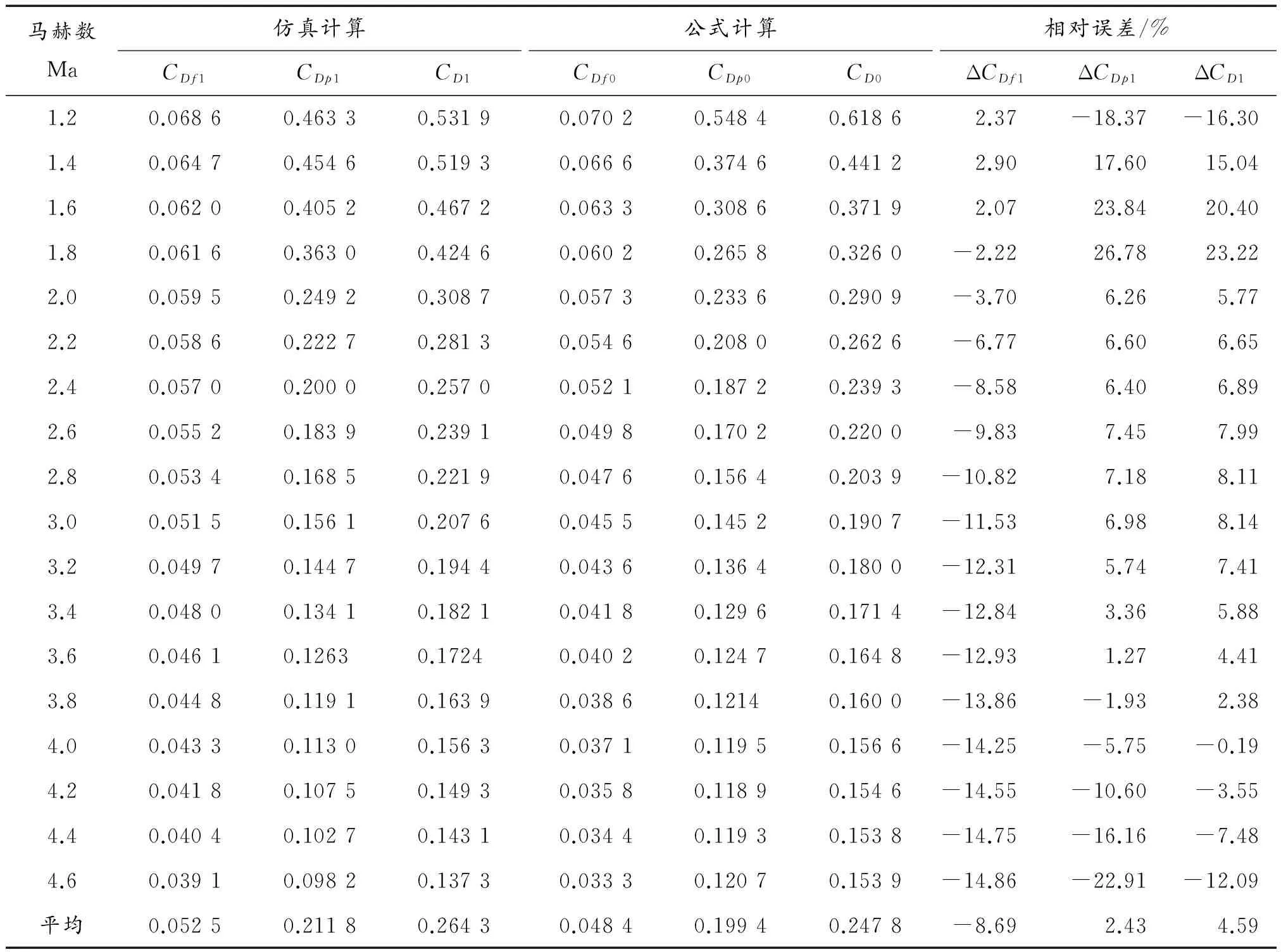
表2　不同馬赫數條件下模型1仿真與公式計算所得阻力系數

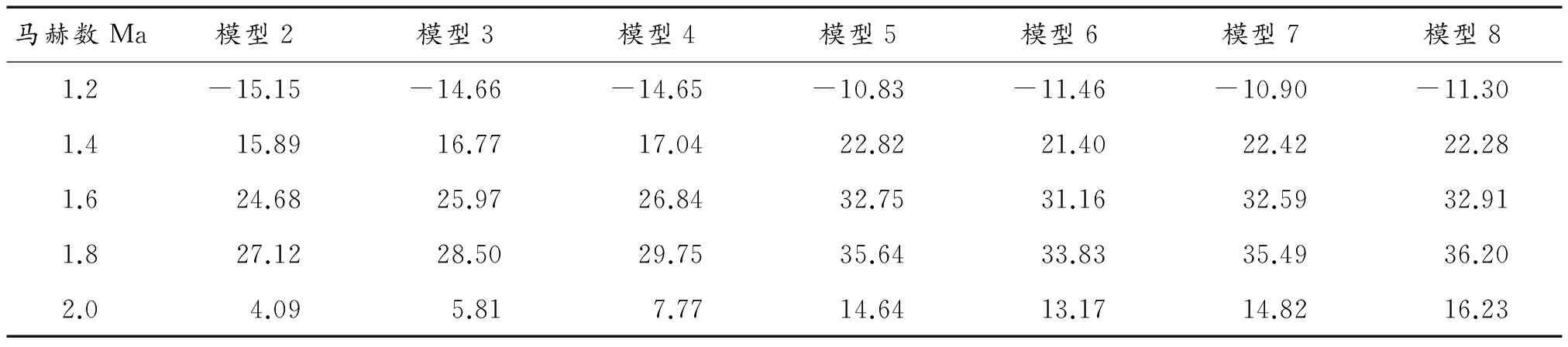
表3　模型2～模型8仿真結果與公式計算結果相對誤差(%)

續表(表2)

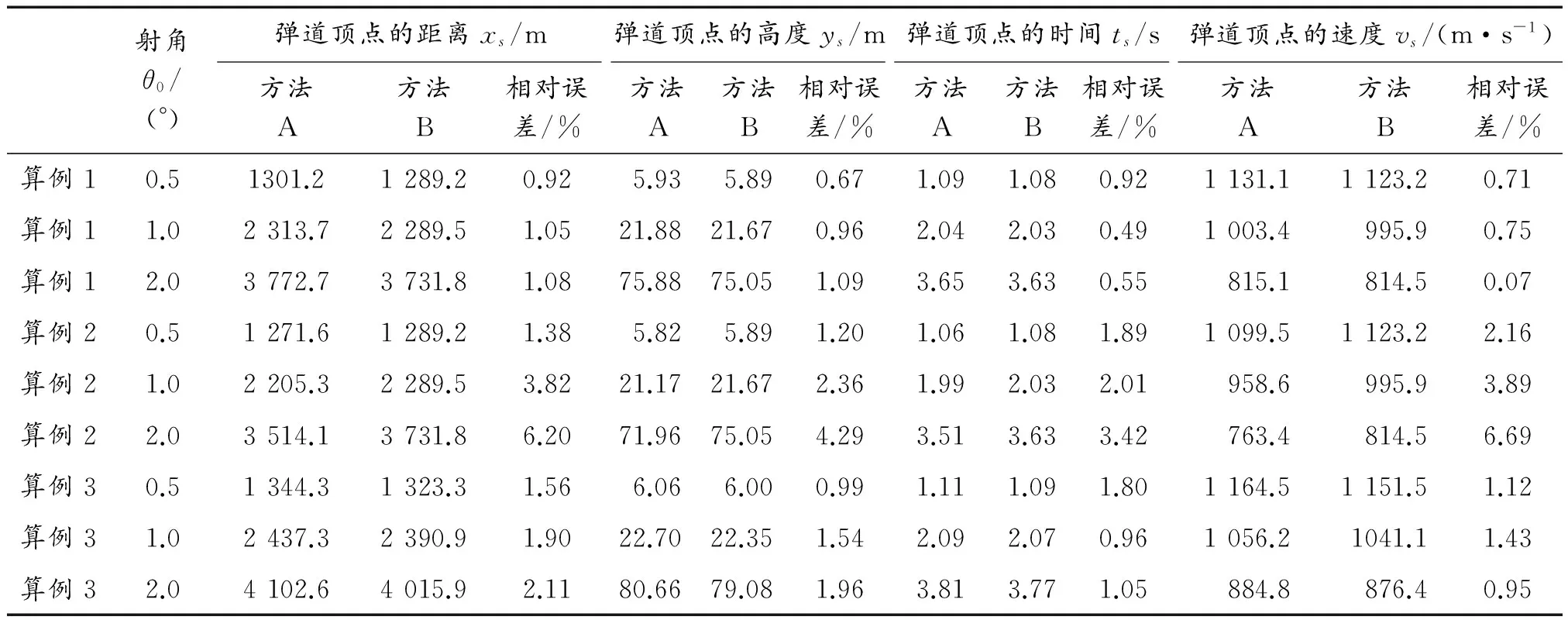
表3　不同射角下用方法A和方法B數值解算的外彈道頂點諸元

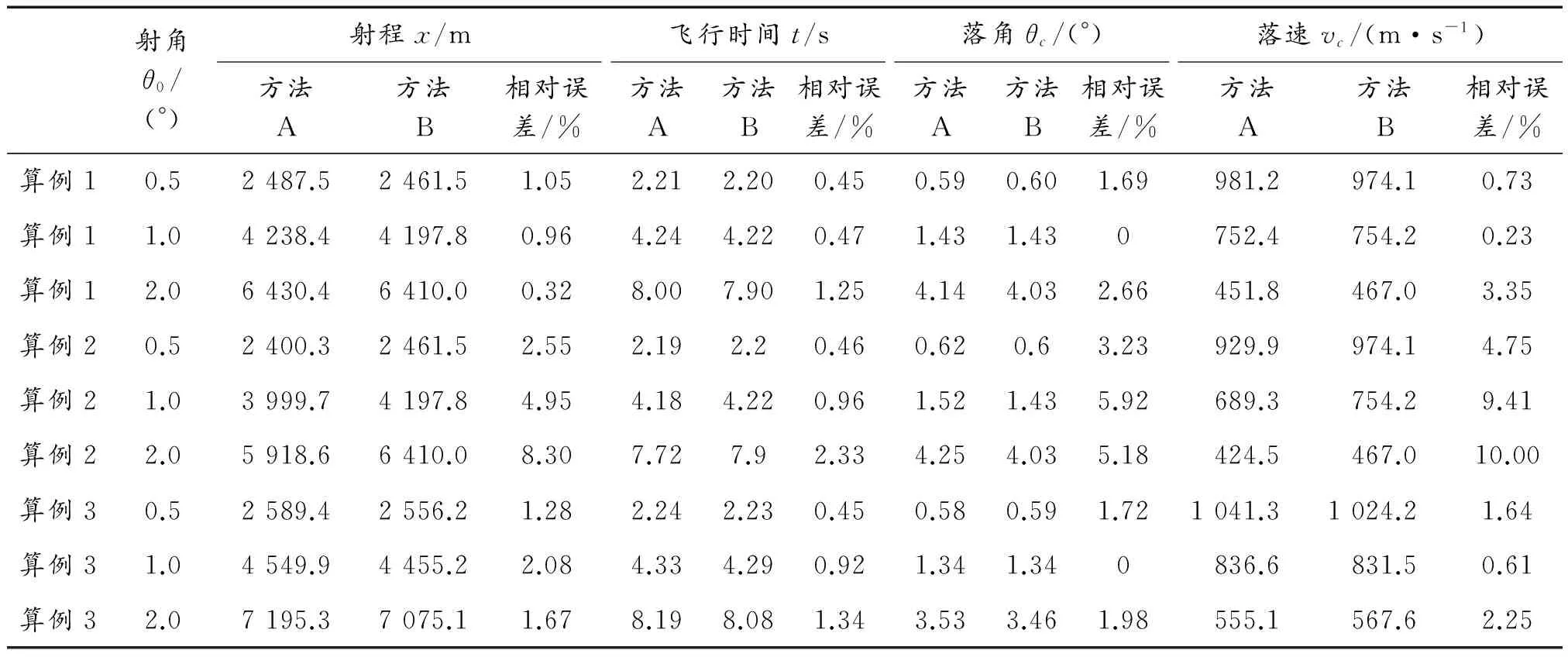
表4　不同射角下用方法A和方法B數值解算的外彈道落點諸元

從表3和表4可以看出，算例1和算例3應用兩種阻力系數解算外彈道所得的外彈道頂點諸元和彈道落點諸元相對誤差很小，在3.35%以內；算例2所得外彈道頂點諸元相對誤差在6.69%以內，落點諸元相對誤差在10%以內。

對于圖1所示的空心彈結構，在特定速度范圍內，用上述兩種方法得到的阻力系數解算外彈道所得頂點諸元與落點諸元相差很小。但在工程設計時，空心彈結構不可能與圖1所示的空心彈簡化結構完全相同。增設彈帶后，仿真所得阻力系數與文獻[13]所給出的公式計算所得阻力系數差別較大，用兩種阻力系數解算外彈道所得頂點諸元與落點諸元相差也較大，因此未考慮彈帶部分影響的空心彈簡化模型阻力系數文獻[13]所給出的計算公式不太適合于工程問題。

4結論

本文應用Fluent軟件對空心彈流場進行數值模擬，分析了不同馬赫數下空心彈的流場特性，將數值仿真得到的空氣動力參數與用文獻[13]所給出的公式計算所得的“理想情況下的”空氣動力參數對比，并分析其差異，對比了應用數值仿真所得阻力系數計算的質點空氣外彈道諸元與應用公式計算所得阻力系數計算的諸元。結果表明：

1) 在來流馬赫數為2.0～4.4的條件下，針對無彈帶結構的簡化的空心彈模型數值模擬所得阻力系數結果與用文獻[13]所給出的公式計算所得阻力系數基本一致，用這兩種阻力系數分別計算空心彈空氣質點外彈道所得頂點諸元和落點諸元相差很小；

2) 空心彈的工程設計與上述簡化的理論模型不可能完全相同，主要差別在彈丸頭部前緣厚度和彈帶結構。其中彈丸頭部前緣厚度在可信區間內對阻力系數影響較小，但彈帶結構對阻力系數的影響較大。增設彈帶后，用兩種方法得到的阻力系數解算質心空氣外彈道所得頂點諸元與落點諸元相差較大，即理想情況下推導出的空心彈簡化模型阻力系數文獻[13]所給出的計算公式不太適合于工程問題求解，此時應以數值仿真為主。

參考文獻：

[1]王雨時.西方國家的空心彈技術[J].彈箭技術,1996,9(3):1-10.

[2]王雨時.西方國家的空心彈技術(續)[J].彈箭技術,1996,9(4):14-22.

[3]周立憲.管式彈丸阻力特性研究[D].南京：南京理工大學,2004.

[4]高旭東,錢建平,王曉鳴,等.基于流場數值模擬的空心彈阻力特性優化方法[J].彈箭與制導學報,2004,24(4):161-162.

[5]高旭東,錢建平,王曉鳴,等.空心彈流場數值模擬與阻力特性[J].南京理工大學學報,2005,29(2):158-161.

[6]任登鳳,譚俊杰,張軍,等.非結構隱式方法在空心彈流場模擬中的應用[J].力學與實踐,2006,10(5):24-27.

[7]錢吉勝,李艷玲,陳志華,等.低阻空心彈流場特性研究[J].彈箭與制導學報,2011,31(4),73-75.

[8]李艷玲,陳志華.口徑30mm空心彈真實條件下的氣動特性研究[J].航空計算技術,2011,41(5):76-80.

[9]李艷玲.低阻空心彈的數值設計研究[D].南京：南京理工大學,2012.

[10]黃振貴,李艷玲,陳志華,等.空心彈的阻力特性與氣動外形數值分析[J].兵工學報,2013,34(5):535-540.

[11]WU J J,SARGENT E R,ROBRET B.High Performance Hollow Projectiles.AD 0768907[R].California:U.S.Department of Commerce National Information Service,1973.

[12]李惠昌,楊金耀,祁榮長.空心彈丸的研究[J].兵工學報,1980,2,32-41.

[13]LAVIOLETT MAURICE A.Tubular Projectile:US,4164904[P].1979-08-21.

[14]LAVIOLETT MAURICE A.Short Range Tubular Projectile:US,4827847[P].1987-02-21.

(責任編輯周江川)

收稿日期：2016-01-25；修回日期：2016-02-20

作者簡介：張浩(1992—)，男，碩士研究生，主要從事引信、彈藥技術研究。 通訊作者：王雨時(1962—)，男，教授，本刊編委，主要從事引戰系統分析與設計研究。

doi:10.11809/scbgxb2016.07.002

中圖分類號：TJ011.2

文獻標識碼：A

文章編號：2096-2304(2016)07-0005-07

Theoretical Calculations and Numerical Simulation on Air Resistance Characteristics of Hollow Projectile

ZHANG Hao，WEN Quan，WANG Yu-shi，ZHANG Zhi-biao

(School of Mechanical Engineering, Nanjing University of Science & Technology, Nanjing 210094, China)

Abstract:Simplified model hollow projectiles with typical design scheme was numerically simulated by Fluent software. The relationship between drag coefficient and Mach number was got. On this basis, trajectory centroid group equations of motion were solved using Matlab software, and the firing data of trajectory vertex and impact point was obtained. Compared the simulation results of drag coefficient above and ballistic firing data with theoretical formula calculation results, its shows that the results of simplified model hollow projectiles between simulation and theoretical calculations has a little difference when incoming flow Mach number between 2.0 and 4.4. Leading edge thickness of hollow projectile has little effect on the drag coefficient in the confidence interval, but rotating band structure has a greater impact on the drag coefficient. Be effected by rotating band structure, the drag coefficient theoretical formula of simplified model hollow projectile is not suitable for solving engineering problem. Engineering design should be based numerical simulation.

Key words:hollow projectile; simulation; theoretical formula; drag coefficient; exterior trajectory

【裝備理論與裝備技術】