一類帶模糊流動性約束的證券投資組合模型

范　國　兵

(湖南財政經濟學院數學與統計學院，湖南長沙410205)

?

一類帶模糊流動性約束的證券投資組合模型

范國兵

(湖南財政經濟學院數學與統計學院，湖南長沙410205)

[摘要]投資組合選擇是投資者在不確定環境下的投資決策問題。基于模糊環境下的證券投資組合，利用梯形模糊數描述投資組合的換手率，建立基于投資組合的凈收益率極大化、熵風險最小化，帶模糊流動性約束的雙目標規劃模型，并給出模型求解方法。

[關鍵詞]投資組合；模糊數；數學模型；證券市場

一、引言

1952年，經濟學家Markowitz在《投資組合的選擇》一文中提出“均值-方差”投資組合選擇模型，奠定了現代金融學的基礎[1]77-91。此后，投資組合選擇問題吸引了國內外眾多學者的研究，并取得了豐碩成果。傳統的研究均假定資產的收益是隨機變量，以概率論為工具進行建模，然而現實金融市場中，證券市場存在許多非隨機因素，投資組合常常不可避免地充滿著模糊隨機性。一些學者借助模糊集理論研究模糊不確定情況下投資組合問題，如Watada 、Tanaka、Vercher等基于模糊投資環境下，對Markowitz均值-方差模型進行了各種形式的推廣[2]219[3]115[4]769。但這些研究都假設投資收益與風險在整個投資期內保持不變的單階段投資組合，對于多階段模糊投資組合模型，國內學者張鵬提出了限制交易成本和交易量，以投資組合收益率的隸屬函數為梯形的多階段均值-半絕對偏差可能性投資組合模型[5]168；劉勇軍等提出了以資產收益和換手率為模糊變量，以資產組合收益與偏度最大，風險、不確定性以及模糊性最小為目標的多準則投資組合優化模型[6]2462。本文利用梯形模糊數描述投資組合的換手率，建立基于投資組合的凈收益率極大化、熵風險最小化、帶模糊流動性約束的雙目標規劃模型，并給出模型求解的方法。

(一) 有關區間數的符號和定義

定義 1：概率分布(p1,p2,…,pn)的熵定義為：

(1)

定義2：模糊數A具有隸屬函數：

(2)

稱A為梯形模型數，其中α、β分別為左右寬度，[a,b]為容許區間。

定義3：設A為梯形模型數，A的λ截集定義為：

[A]λ=[a-(1-λ)α,b+(1-λ)β]

(3)

此時，A的可能性均值定義為：

(4)

定義4：設A,B為兩個梯形模糊數，定義A≤B當且僅當E(A)≤E(B)。

二、模型建立

假設投資者(或資產管理者)在n只股票中選出若干只進行組合投資，根據股票的歷史收益資料分析，推斷其未來的收益趨勢，不妨收集過去的收益資料l天，記第i只股票在這l天中的收益率序列為ri1,ri2,…ril(i=1,2,…n),設：

將區間[a,b]分成m個小區間，[r0,r1],[r1,r2],…,[rm-1,rm]，

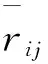
(5)

(6)

引入如下記號：

xi：將投資在風險資產i(i=1,2,…,n)或無風險資產(i=n+1)上的投資比例；

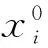
ki：證券市場資產i(i=1,2,…,n+1)的交易費比率；

mi：證券市場資產i(i=1,2,…,n+1)的投資比例上界。

假定投資組合調整過程中沒有注入新的資金，采用V型交易數函數，考慮與交易數量成正比的交易費用，投資組合x=(x1,x2,…,xn)的總交易費用為：

(7)

(8)

(9)

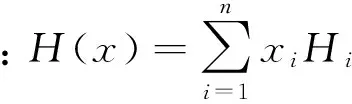
(10)

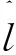
(11)

建立基于投資組合的凈收益極大化、熵風險最小化的規劃模型：

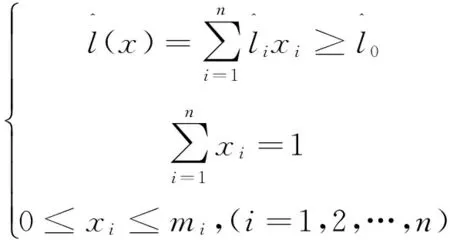
(M1)

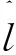
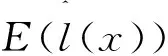
從而M1等價于：

(M2)

三、模型求解

模型M2為雙目標規劃問題，轉化為如下單目標規劃問題：

(M3)

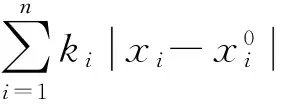
(M4)

從而模型M4可以轉化成如下標準的線性規劃問題：

(M5)

對于標準線性規劃問題M5，利用軟件包LINGO和LINDO即可求解。

四、 結語

本文利用梯形模糊數來描述投資組合的換手率，以投資組合的凈收益率極大化、熵風險最小化，建立了帶模糊流動性約束的證券投資組合雙目標規劃模型，并將該模型轉化成線性規劃模型，從而可以利用成熟的軟件包來求解，該模型對證券投資選擇具有一定的使用價值和指導意義。證券市場中，投資收益、風險和流動性都具有模糊不確定性，針對證券投資組合選擇問題，怎樣運用模糊數學理論和最優化方法等工具進行系統、深入研究，構建具有實踐價值的投資組合選擇模型，為投資決策建立分析框架，始終具有較大的理論意義和實踐意義。

[參考文獻]

[1]Markowitz H M.Portfolio selection[J]. Journal of Finance, 1952，(7).

[2]Watada J.Fuzzy portfolio selection and its applications to decision making[J].Tatra Mountains Mathematical Publication, 1997，(13).

[3]Tanaka H, Guo P. Portfolio selection based on upper and lower exponential possibility distributions[J]. EuropeanJournal of Operational research , 1999，(114).

[4]Vercher E, Bermudez J, Segura J. Fuzzy portfolio optimization under downside risk measures[J].Fuzzy Sets and Systems,2007，(158).

[5]張鵬.多階段均值-半絕對偏差模糊投資組合優化研究模[J].糊系統與數學. 2013,27(2).

[6]劉勇軍,等,考慮現實約束的模糊多準則投資組合優化模型[J].系統工程理論與實踐,2013, 33 (10).

(責任編輯魯守博)

[收稿日期]2016-03-23

[基金項目]湖南省社科基金資助項目“基于過程能力指數的貝葉斯統計分析及其應用研究”(YBA2015065)。

[作者簡介]范國兵,男，湖南長沙人，湖南財政經濟學院數學與統計學院副教授。

[中圖分類號]F830.91

[文獻標識碼]A

[文章編號]1672-0040(2016)04-0011-03