一種應(yīng)對窄帶主動噪聲控制中頻率不匹配的方法

夏國芳，劉　劍

（南京航空航天大學(xué) 自動化學(xué)院，南京 211106）

?

一種應(yīng)對窄帶主動噪聲控制中頻率不匹配的方法

夏國芳，劉劍

（南京航空航天大學(xué) 自動化學(xué)院，南京 211106）

摘要：窄帶前饋主動噪聲控制系統(tǒng)中，參考信號通常通過非聲學(xué)傳感器獲取。由于傳感器老化磨損等原因，所測同步頻率與目標噪聲真實頻率間將存在誤差，即產(chǎn)生頻率不匹配（FM）。結(jié)合AR模型，提出一種改進的FM補償方法，加入一個延遲模塊和一個相應(yīng)的幅值相位調(diào)節(jié)器，本質(zhì)上是通過延遲和疊加構(gòu)造出隱含真實頻率的信號，同時提高相位匹配速度和精度。仿真結(jié)果與分析表明，設(shè)計的FM補償方法能有效應(yīng)對15%以上的頻率不匹配量，且系統(tǒng)收斂速度更快。

關(guān)鍵詞：聲學(xué)；窄帶主動噪聲控制；頻率不匹配；延遲；幅值相位調(diào)節(jié)

窄帶噪聲往往是由旋轉(zhuǎn)設(shè)備或具有往復(fù)運動的裝置產(chǎn)生，如風(fēng)機、引擎和大規(guī)模切割機械等設(shè)備產(chǎn)生的噪聲，具有周期或者近似周期性特征。因此，窄帶噪聲實質(zhì)上是正弦型諧波噪聲，在數(shù)學(xué)上可以用正、余弦函數(shù)來表示[1]。通常，這些噪聲的頻率是未知的，幅值和相位隨時間變化。在環(huán)境和工程系統(tǒng)中，消除或削弱這些噪聲，尤其是低頻成分，顯得尤為重要[2–5]。主動噪聲控制（Active Noise Control, ANC）技術(shù)由于在抑制低頻諧波噪聲方面的有效性而備受關(guān)注，并習(xí)慣將用于抑制這種窄帶噪聲的ANC系統(tǒng)稱之為窄帶ANC系統(tǒng)。

窄帶噪聲源具有特殊的運動方式，因此，在窄帶前饋ANC系統(tǒng)中，為了避免可能發(fā)生的聲反饋，參考信號往往利用非聲學(xué)傳感器（如轉(zhuǎn)速計）獲取，即通過簡單線性回歸方法從非聲學(xué)傳感器測得的同步信號（如轉(zhuǎn)速等）解算出噪聲頻率，信號發(fā)生器再根據(jù)該頻率產(chǎn)生相應(yīng)參考信號[6，7]。若非聲學(xué)傳感器長時間運行產(chǎn)生了疲勞磨損，或者信號發(fā)生器存在誤差，將導(dǎo)致參考信號頻率與目標噪聲頻率不一致，即發(fā)生了頻率不匹配（Frequency Mismatch,FM）現(xiàn)象[8]。FM對窄帶前饋ANC系統(tǒng)而言是致命的，即使存在較小的頻率不匹配量，系統(tǒng)也將無法有效消除目標噪聲[9]。因此，開發(fā)設(shè)計應(yīng)對窄帶ANC系統(tǒng)中頻率不匹配的方法顯得尤為重要。Xiao,Sakai, Hinamoto以及Jeon等均對FM問題進行了研究[8–12]。目前，應(yīng)對FM問題的方法主要有Xiao提出的自回歸（AR）模型方法[10]和Jeon提出的最小方差不失真響應(yīng)（MVDR）譜方法[9]。MVDR譜方法涉及復(fù)雜的頻率估計，相較于AR模型方法要復(fù)雜得多。AR模型結(jié)構(gòu)簡單，計算復(fù)雜度低。Xiao利用的2階AR模型本質(zhì)上形成了一個自適應(yīng)2階陷波濾波器，通過參數(shù)的不斷調(diào)整，達到產(chǎn)生精確頻率的參考信號，從而有效應(yīng)對頻率不匹配。基于AR模型，黃等結(jié)合變步長算法，設(shè)計了一種應(yīng)對非平穩(wěn)頻率不匹配的窄帶ANC系統(tǒng)[13]。

本文基于AR模型，進一步對系統(tǒng)進行改進設(shè)計，提出利用延遲模塊及相應(yīng)的幅值相位調(diào)節(jié)器可使新的窄帶ANC系統(tǒng)在應(yīng)對FM中的性能得到提高。在給出改進系統(tǒng)的同時，基于Fx LMS算法詳細推導(dǎo)了各自適應(yīng)參數(shù)的更新方程，通過計算仿真，驗證了改進系統(tǒng)在應(yīng)對FM方面的有效性。

1　傳統(tǒng)組合器型窄帶ANC系統(tǒng)

典型的組合器型窄帶ANC系統(tǒng)如圖1所示，噪聲p(n)表示為

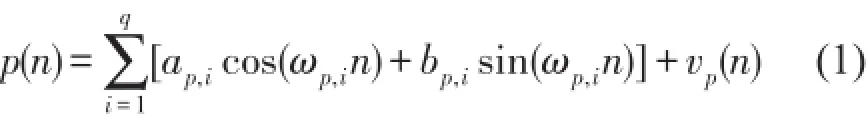
其中q是頻率成分個數(shù)，ωp,i是第i個頻率分量，是噪聲信號的離散傅里葉系數(shù)，vp(n)是背景噪聲，通常設(shè)為均值為0方差為的高斯白噪聲。

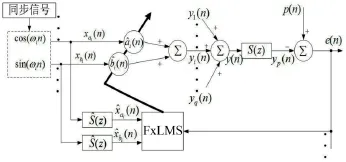
圖1　傳統(tǒng)組合器型窄帶ANC系統(tǒng)（第i個頻率通道）

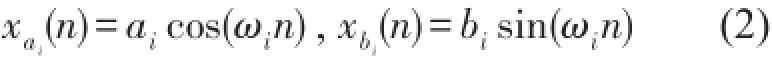
參考信號為ωi是由非聲學(xué)傳感器獲得的同步信號按線性關(guān)系計算得到的第i個頻率通道的參考信號頻率。為參考信號的幅值系數(shù)。根據(jù)圖1，第i個頻率通道的輸出yi(n)表示為

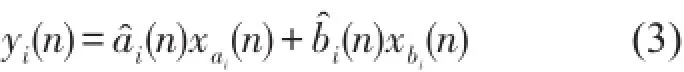
用于更新控制濾波器權(quán)值的Fx LMS算法為

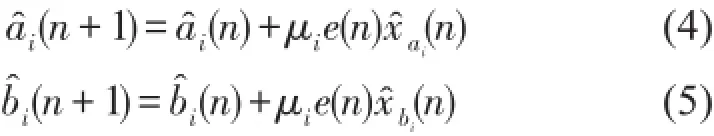
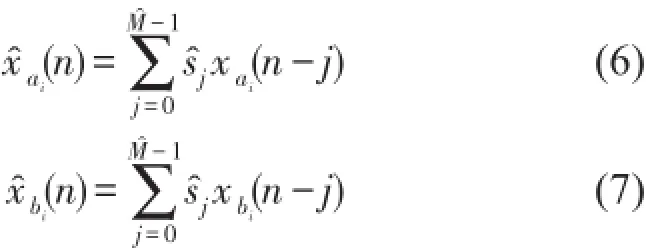
其中μi為更新補償因子；為濾波-x信號，是由參考信號經(jīng)次級通道S(z)的估計S?(z)濾波而得，即分別是次級通道估計模型S?(z)的長度和單位沖擊響應(yīng)系數(shù)。在線性窄帶ANC系統(tǒng)中，次級通道S(z)及其估計S?(z)通常可用FIR濾波器表示，即分別是次級通道S(z)的長度和單位沖擊響應(yīng)系數(shù)。次級通道可采用離線或在線的系統(tǒng)辨識技術(shù)進行估計，如自適應(yīng)LMS算法或維納濾波器[14]。

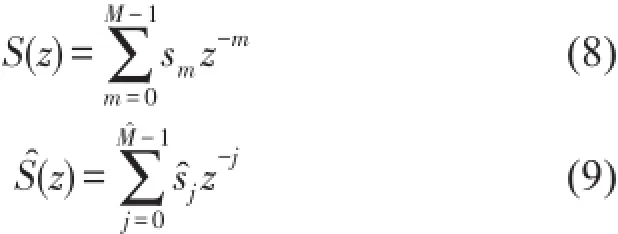
系統(tǒng)殘余噪聲信號e(n)由下式計算得到相應(yīng)的，M和

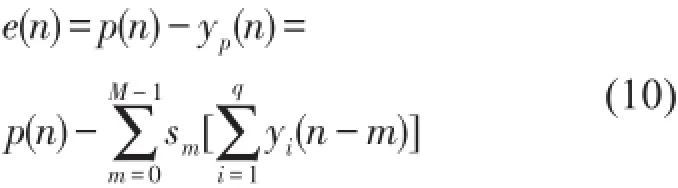
頻率偏差定義為

當系統(tǒng)不存在FM，即Δωi=0時，圖1所示系統(tǒng)對目標噪聲有很好的抑制效果，如圖2(a)所示。圖2 (b)給出當系統(tǒng)FM（:=|Δωi|/ωp,i×100%）僅為1%時，傳統(tǒng)窄帶ANC系統(tǒng)噪聲抑制性能就將快速下降[8，15]。因此，對參考信號的頻率失調(diào)進行補償是十分重要的。

從計算簡便、易用的角度出發(fā)，本文在傳統(tǒng)窄帶ANC系統(tǒng)基礎(chǔ)上，結(jié)合AR模型[10]，設(shè)計延遲模塊及相應(yīng)濾波器對頻率進行補償，使得新系統(tǒng)能夠應(yīng)對較大的FM量。

2　基于延遲的頻率補償

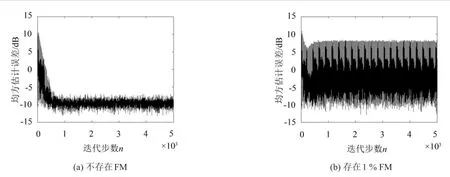
圖2　窄帶前饋ANC系統(tǒng)殘余噪聲水平

Xiao等在研究FIR型窄帶ANC系統(tǒng)的過程中，設(shè)計了利用2階AR模型應(yīng)對一定程度FM的方法[10]。考慮組合器型窄帶ANC系統(tǒng)在抑制窄帶噪聲中的有效性，結(jié)合AR模型，本文設(shè)計了一種新的應(yīng)對FM的窄帶ANC系統(tǒng)。如圖3所示，在第i頻率通道中，通過引入一個延遲模塊，改變參考信號的相位，再經(jīng)過相應(yīng)自適應(yīng)組合器的調(diào)節(jié)，提高了次級源與目標噪聲源在幅值和相位上的匹配速度和精度，使新系統(tǒng)在應(yīng)對FM量上得到提高的同時，收斂速度也得到提升。整體表現(xiàn)上，系統(tǒng)的魯棒性得到了提高。參數(shù)k的取值直接影響參考信號相位改變的程度，通過三角函數(shù)的運算，不難發(fā)現(xiàn)，該值本質(zhì)上影響次級源幅值和相位調(diào)節(jié)，間接影響系統(tǒng)的動態(tài)和穩(wěn)態(tài)性能。

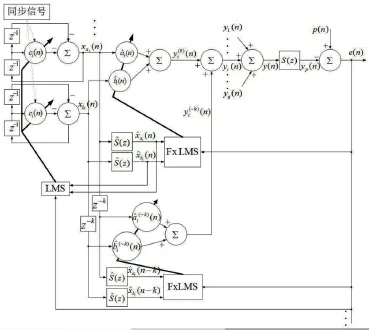
圖3　加延遲的頻率失調(diào)補償ANC系統(tǒng)（第i頻率通道）

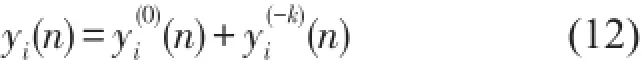
在圖3所示系統(tǒng)中，對于第i個頻率通道，次級源由兩部分構(gòu)成，即其中由一個組合器合成得到，yi(-k)(n)由延遲模塊和相應(yīng)組合器合成得到

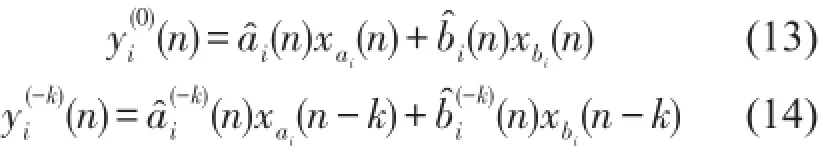
各頻率通道輸出的次級源疊加后經(jīng)次級通道S(z)，再與目標噪聲 p(n)干涉相消，得到殘余噪聲

e(n)。則系統(tǒng)殘余噪聲信號e(n)表示為

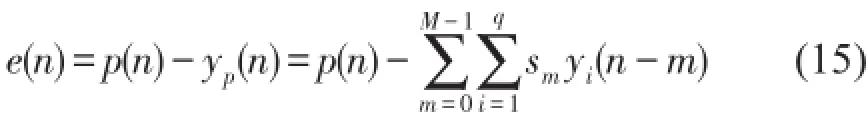
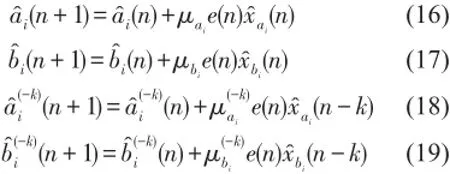
ci(n)是與參考信號頻率相關(guān)的動態(tài)參數(shù)，其初始值設(shè)為-2coswi。考察代價函數(shù)

依據(jù)最速梯度下降法，可推導(dǎo)出用于更新參數(shù)ci(n)的LMS算法為

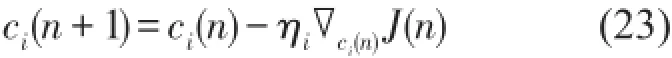
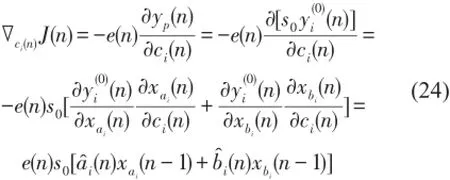
其中梯度?ci(n)J(n)計算如下根據(jù)式(24)，最終得到用于更新參數(shù)ci(n)的

Fx LMS算法為其中 μc=ηis0為步長因子。

與僅有AR模型相比，基于延遲的頻率補償算法計算量有所增加，主要體現(xiàn)在延遲通道的幅值相位調(diào)節(jié)器。具體地，每一步迭代中，在次級源yi(n)的計算中增加了2個乘法和2個加法，在控制系數(shù)和的更新中分別增加了2個乘法和1個加法，共增加6個乘法和3個加法。一般情況下，取，即共增加5個乘法和3個加法。可見，系統(tǒng)的改進帶來的計算量增加是十分有限的。然而，仿真實驗表明，有限的計算量增加卻能夠極大提升系統(tǒng)的性能。因此，延遲模塊的引入，對于FM的應(yīng)對是十分有效的。

3　仿真計算與分析

針對不同頻率不匹配情形，對僅依賴AR模型的頻率補償方法和圖3中加延遲的頻率補償方法進行了大量仿真計算與分析。

仿真計算中，次級通道S(z)設(shè)為一個長度為12 （M=12）、截止頻率為0.4 π的FIR濾波器。次級通道估計模型S?(z)用自適應(yīng)LMS算法通過離線辨識得到，長度設(shè)為12（M?=12）。考察3個頻率通道情形，即q=3。計算中所有期望值通過執(zhí)行40次獨立運算后取集平均進行逼近。其它基本仿真條件如表1所示。

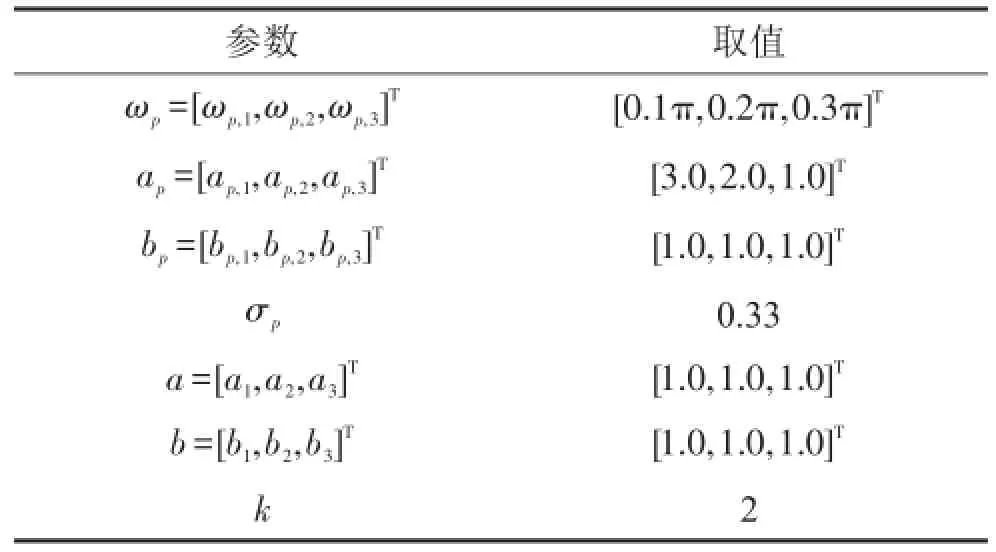
表1　基本仿真條件

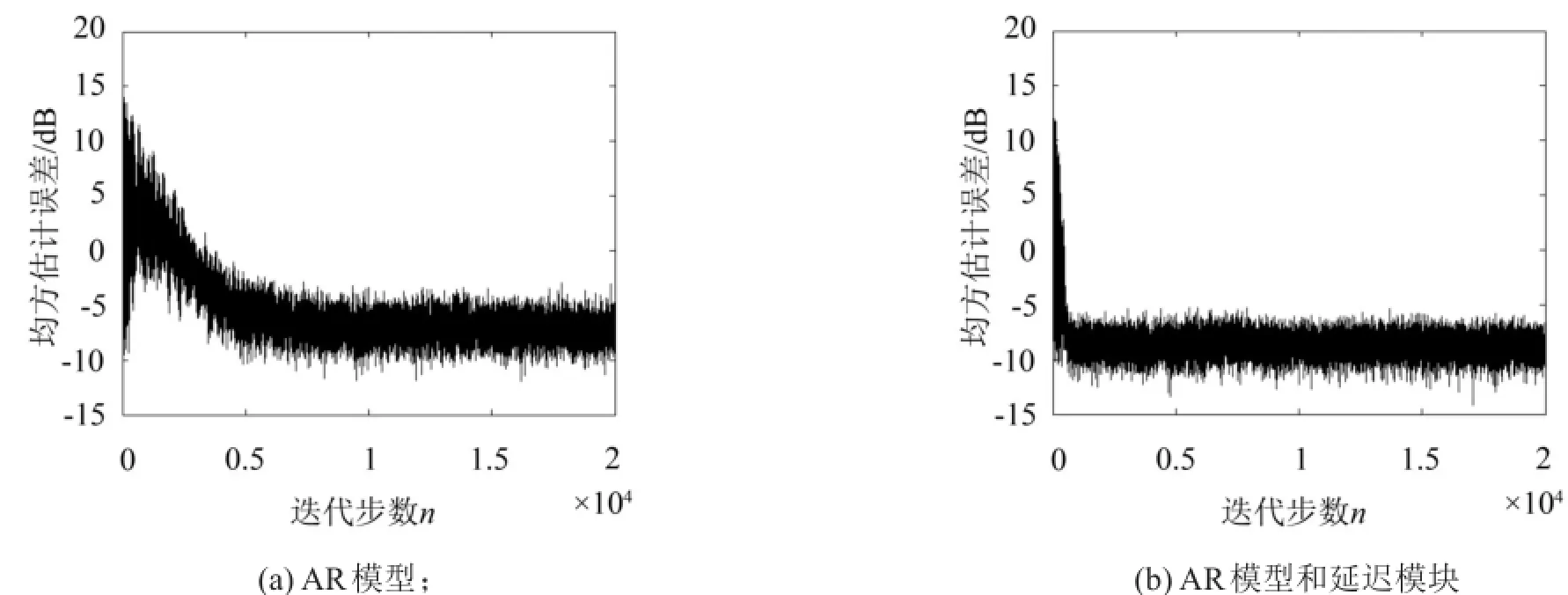
圖4　FM為5%時的系統(tǒng)殘余噪聲能量比較

圖4—圖6分別給出了FM為5%、10%和15%時兩個系統(tǒng)性能的比較結(jié)果。在得到圖4(a)的仿真過程中，更新步長因子取為 μai=μbi=0.05（對所有i）、μc=[μc1,μc2,μc3]T=[0.000 1，0.000 25，0.000 5]T；對于圖4(b)，步長因子取值為 μai=μbi=0.025（對所有i） 、 μc=[0.000 25，0.000 25，0.001]T及（對所有i）。由圖4可知，當窄帶ANC系統(tǒng)中存在5%的FM時，本文提出增加延遲模塊系統(tǒng)在步長因子取值相對較小情況下，收斂速度明顯比僅依賴AR模型的系統(tǒng)要快，且獲得更小的穩(wěn)態(tài)殘余噪聲能量（參見表2），更接近背景噪聲能量（即-10 dB）。對于10%FM情形，兩系統(tǒng)各補償因子取值不變，不難得到相同的結(jié)論（參加圖5和表2）。特別地，分析圖6和表2可知，當窄帶ANC系統(tǒng)中有高達15%的FM時，僅依賴AR模型難以有效補償FM，而增加延遲模塊即可得到有效補償。需要說明的是，為了提高系統(tǒng)性能，圖6(a)中補償因子μc=[μc1，μc2，μc3]T=[0.000 25，0.000 25，0.000 5]T，其他參數(shù)不變。結(jié)合其它大量仿真，結(jié)果顯示增加延遲模塊可以極大提高系統(tǒng)的魯棒性，提高系統(tǒng)應(yīng)對FM的能力。

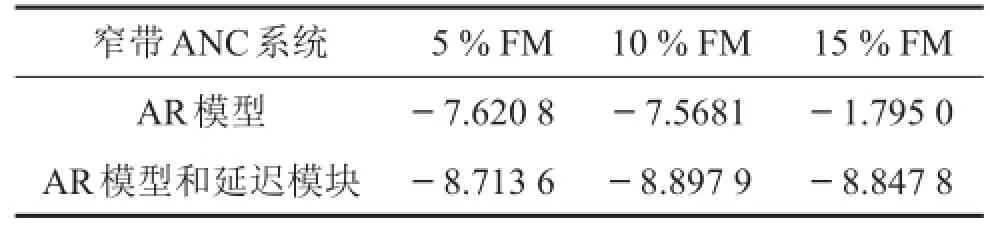
表2　穩(wěn)態(tài)誤差比較單位：dB

系統(tǒng)收斂特性由系統(tǒng)中的自適應(yīng)參數(shù)控制，為了進一步觀察本文提出系統(tǒng)中各自適應(yīng)參數(shù)的特性，圖7給出了FM為5%時各參數(shù)的變化趨勢。圖7(a)—圖7(e)分別對應(yīng)線性組合器權(quán)值以及AR模型參數(shù)ci(n)。從圖7看出，當系統(tǒng)達到穩(wěn)態(tài)時，系統(tǒng)主控制器各參數(shù)并沒有明顯的穩(wěn)態(tài)值，即存在一定的慢速波動。但它們之間存在耦合，受相互之間約束，即使有波動，也不會導(dǎo)致整個系統(tǒng)發(fā)散。系統(tǒng)通過不斷調(diào)整AR模型參數(shù)ci(n)使參考信號頻率逼近真實噪聲頻率，從而有效應(yīng)對頻率不匹配。可見，ci(n)的變化趨勢和系統(tǒng)收斂趨勢息息相關(guān)，從圖7也可看出，ci(n)和系統(tǒng)收斂特性較為一致。另外，系統(tǒng)增加延遲模塊后，延遲和疊加構(gòu)造出隱含真實頻率的信號，各頻率通道的兩個線性組合器共同作用，有效提高了系統(tǒng)的收斂速度和魯棒性。

圖5　FM為10%時的系統(tǒng)殘余噪聲能量比較

圖6FM為15%時的系統(tǒng)殘余噪聲能量比較

在上述仿真計算中，設(shè)定的延遲模塊的延遲量k=2，為了進一步定性分析該取值的合理性以及考察延遲量對系統(tǒng)性能的影響，圖8和表3分別給出了FM為5%情形下，系統(tǒng)穩(wěn)態(tài)MSE相對于k值的關(guān)系以及系統(tǒng)收斂速率的比較。需要說明的是，在計算過程中，所有步長因子固定不變。圖8顯示，當k取2時，系統(tǒng)穩(wěn)態(tài)誤差相對較小，從使系統(tǒng)穩(wěn)態(tài)誤差最小化考慮該值比較合理。表3顯示，當k取2時，系統(tǒng)收斂速率也相對較快，從系統(tǒng)動態(tài)性能考慮該值也較合理。同時，不難發(fā)現(xiàn)，當k取12時，系統(tǒng)穩(wěn)態(tài)性能和動態(tài)性能同樣較好，顯然k的取值不是唯一的，原因在于窄帶噪聲信號本身具有周期性。然而，k值的周期性與信號周期性以及FM的定量關(guān)系，需要更加深入的分析。

圖8　系統(tǒng)穩(wěn)態(tài)MSE與k值的關(guān)系變化

4　結(jié)　語

針對窄帶ANC系統(tǒng)中存在FM的問題，本文提出了一種AR模型與延遲模塊相結(jié)合的組合器型窄帶ANC系統(tǒng)。通過大量仿真驗證，該系統(tǒng)在應(yīng)對FM中具有有效性，且新系統(tǒng)相較于僅含AR模型的系統(tǒng)應(yīng)對FM能力更強，收斂速率更快，顯示該系統(tǒng)的動態(tài)和穩(wěn)態(tài)性能均有較大提高。后續(xù)研究可擴展但不局限于：(1)FM與延遲因子的定量關(guān)系及該因子的優(yōu)化；(2)通過系統(tǒng)性能分析，深入考察系統(tǒng)穩(wěn)態(tài)MSE與FM的關(guān)系，從而設(shè)計出更加有效的應(yīng)對結(jié)構(gòu)和算法。

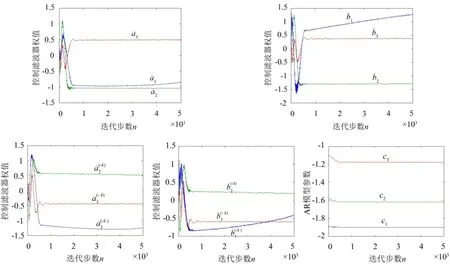
圖7　系統(tǒng)中各自適應(yīng)參數(shù)的變化趨勢

表3　系統(tǒng)收斂速率比較

參考文獻：

[1]Xiao Y,Tadokoro Y,Shida K.Adaptive algorithm based on least mean p-power error criterion for Fourier analysis in additivenoise[J].IEEETransactionsonSignal Processing,1999,47(4):1172-1181.

[2]Xiao Y,Ikuta A,Ma L,et al.Stochastic analysis of the FXLMS-based narrowband active noise control system[J]. IEEE Transactions on Audio,Speech,and Language Processing,2008,16(5):1000-1014.

[3]Wang L,Gan W S.Convergence analysis of narrowband active noise equalizer system under imperfect secondary pathestimation[J].IEEETransactionsonAudio, Speech,and Language Processing,2009,17(4):566-571.

[4]陳曉東，陳錦棟.淺析220 kV室內(nèi)變電站的噪聲控制[J].噪聲與振動控制,2013，33(6)：220-223.

[5]胡佳杰，左曙光，何呂昌，等.燃料電池汽車空輔系統(tǒng)噪聲有源控制技術(shù)[J].噪聲與振動控制，2013,33(1)：83-89.

[6]Bodson M,Douglas S C.Adaptive algorithms for the rejectionofsinusoidaldisturbanceswithunknown frequency[J].Automatica,1997,33(12):2213-2221.

[7]Pigg S,Bodson M.Adaptive algorithms for the rejection of sinusoidal disturbances acting on unknown plants[J]. IEEE Transactions on Control Systems Technology, 2010,18(4):822-836.

[8]Xiao Y,Ma L,Khorasani K.A robust narrowband active noisecontrolsystemforaccomodatingfrequency mismatch[M].na,2004.

[9]Jeon H J,Chang T G,Kuo S M.Analysis of frequency mismatch in narrowband active noise control[J].IEEE TransactionsonAudio,Speech,andLanguage Processing,2010,18(6):1632-1642.

[10]Xiao Y,Ma L,Khorasani K,et al.A new robust narrowband active noise control system in the presence of frequency mismatch[J].IEEE Transactions on Audio, Speech,and Language Processing,2006,14(6):2189-2200.

[11]Sakai H,Hinamoto Y.An exact analysis of the LMS algorithm with tonal reference signals in the presence of frequency mismatch[J].Signal Processing,2005,85(6): 1255-1262.

[12]Hinamoto Y,Sakai H.A filtered-X LMS algorithm for sinusoidal reference signals-effects of frequency mismatch [J].IEEE Signal Processing Letters,2007,14(4):259-262.

[13]黃博妍，常琳，馬亞平，等.一種應(yīng)對非平穩(wěn)頻率失調(diào)的窄帶主動噪聲控制系統(tǒng)[J].自動化學(xué)報，2015，41(1)：186-193.

[14]Williamson G A,Clarkson P,Sethares W A.Performance characteristics of the median LMS adaptive filter[J].IEEE Transactions on Signal Processing,1993,41(2):667-680.

[15]Xiao Y,Ma L,Khorasani K,et al.A filtered-X RLS based narrowband active noise control system in the presence of frequency mismatch[A].IEEE International Symposium on Circuits and Systems[C].Kobe,Japan:IEEE,May 23-26,2005.260-263.

要研究方向為主動噪聲控制。

E-mail:jliu@nuaa.edu.cn

中圖分類號：TB535

文獻標識碼：A

DOI編碼：10.3969/j.issn.1006-1335.2016.01.006

文章編號：1006-1355(2016)01-0026-06

收稿日期：2015-08-07

基金項目：國家自然科學(xué)基金（61201364）

作者簡介：夏國芳（1991-），女，江蘇泰州人，碩士研究生，主

通訊作者：劉劍，男，碩士生導(dǎo)師。

AMethod forAccommodating Frequency Mismatch in NarrowbandActive Noise Control

XIA Guo-fang,LIUJian

(College ofAutomation Engineering,Nanjing University ofAeronautics andAstronautics, Nanjing 211106,China)

Abstract:In a narrowband active noise control(ANC)system,the reference signals are usually generated through nonacoustic sensors.The measured synchronous frequencies of the reference signals will be different from the true frequencies of the objective noise due to the sensor’s aging or fatigue accumulation.This difference is referred as frequency mismatch (FM).In this paper,based on AR model,an improved FM compensation method was proposed by adding a delay module and a corresponding amplitude and phase adjuster.In fact,this method constructs the signals containing implied true frequencies through delays and superposition so as to raise the phase matching rate and accuracy.Simulation and analysis show that the designed FM compensation method can effectively deal with more than 15%of the FM with faster convergence rate.

Key words:acoustics;narrowband active noise control;frequency mismatch(FM);delay;amplitude and phase adjustment