邊坡可靠度分析中巖土合理樣本數(shù)目探討

趙晶，蔣良濰，羅強(qiáng)，駱飛，孔德惠

(1.西南交通大學(xué) 土木工程學(xué)院，四川 成都 610031；2.高速鐵路線路工程教育部重點(diǎn)實(shí)驗(yàn)室，四川 成都 610031)

?

邊坡可靠度分析中巖土合理樣本數(shù)目探討

趙晶1,2，蔣良濰1,2，羅強(qiáng)1,2，駱飛1,2，孔德惠1,2

(1.西南交通大學(xué) 土木工程學(xué)院，四川 成都 610031；2.高速鐵路線路工程教育部重點(diǎn)實(shí)驗(yàn)室，四川 成都 610031)

摘要:土工參數(shù)由有限樣本數(shù)目勘察取樣試驗(yàn)結(jié)果的估計(jì)推斷而得到，統(tǒng)計(jì)不確定性將對(duì)可靠度分析結(jié)果帶來誤差，因此合理樣本數(shù)目應(yīng)體現(xiàn)分析結(jié)果精度與勘察費(fèi)用間矛盾的協(xié)調(diào)。基于從土工參數(shù)總體分布中隨機(jī)抽樣的方法模擬某一樣本容量下的勘察取樣試驗(yàn)，以120次重復(fù)抽樣構(gòu)建樣本統(tǒng)計(jì)值空間，分析樣本統(tǒng)計(jì)值及對(duì)應(yīng)邊坡可靠度指標(biāo)的離散特征。根據(jù)樣本容量對(duì)可靠度指標(biāo)計(jì)算結(jié)果空間散布范圍的約束效應(yīng)，探討土工強(qiáng)度參數(shù)變異水平呈小、中和大3個(gè)等級(jí)時(shí)相對(duì)應(yīng)的合理樣本數(shù)目。計(jì)算分析表明：樣本數(shù)目增加可減小可靠指標(biāo)分布的離散程度，土工參數(shù)變異性增大則反之；為保證可靠度分析結(jié)果精度，在土工參數(shù)變異性增大條件下須相應(yīng)增加樣本數(shù)目；可靠度指標(biāo)變異系數(shù)取0.30時(shí)，對(duì)應(yīng)于參數(shù)呈小、中和大變異水平的樣本數(shù)目分別為6，11和18。研究成果對(duì)完善工程勘察中的土工試驗(yàn)取樣數(shù)目有一定參考價(jià)值。

關(guān)鍵詞：邊坡可靠度分析；樣本數(shù)目；統(tǒng)計(jì)不確定性；可靠度指標(biāo)；散布范圍；變異系數(shù)；隨機(jī)抽樣

邊坡穩(wěn)定性是巖土工程涉及的重要內(nèi)容之一，以概率理論為基礎(chǔ)、考慮各種不確定性的可靠度設(shè)計(jì)方法已開始進(jìn)入實(shí)用階段。可靠度分析中，土工參數(shù)的不確定性主要可分為2類，即土體本身固有變異性和系統(tǒng)的不確定性[1]。前者源于長期地質(zhì)生成作用，變異性客觀存在，但如果進(jìn)行大量樣本勘察試驗(yàn)，則能準(zhǔn)確得到土工參數(shù)的分布特征。后者包括統(tǒng)計(jì)不確定性、試驗(yàn)不確定性和模型不確定性。其中，統(tǒng)計(jì)不確定性是由于樣本數(shù)目有限，導(dǎo)致采用樣本統(tǒng)計(jì)值對(duì)總體分布概型及參數(shù)的估計(jì)不盡準(zhǔn)確，呈現(xiàn)統(tǒng)計(jì)值圍繞真值散布的現(xiàn)象，從而影響可靠度分析結(jié)果的精度。通過勘探取樣獲取強(qiáng)度指標(biāo)可看作從總體中隨機(jī)抽取樣本的過程。巖土參數(shù)固有不確定性從數(shù)學(xué)角度可以用連續(xù)分布的隨機(jī)變量加以描述，勘察數(shù)據(jù)是從中進(jìn)行的有限樣本容量的抽樣。由于資金、時(shí)間、試驗(yàn)條件等因素限制，工程實(shí)際中僅能得到較少的樣本個(gè)數(shù)，通過樣本數(shù)據(jù)推斷的概率分布與真實(shí)分布間存在偏差，巖土參數(shù)統(tǒng)計(jì)值偏離真值，樣本容量越少，偏差在概率意義上越顯著。保證邊坡穩(wěn)定可靠度分析結(jié)果精度應(yīng)建立在準(zhǔn)確的分布概型和總體參數(shù)的基礎(chǔ)上，以小樣本統(tǒng)計(jì)值代入可靠度計(jì)算會(huì)相應(yīng)引起偏差。由于抽樣隨機(jī)性，每批次抽樣的計(jì)算結(jié)果具有差異，造成結(jié)果離散，可信度不高。但隨著樣本容量增大，這種差異會(huì)逐漸減小。因此，在滿足邊坡設(shè)計(jì)可靠度的精度要求條件下，通過約束結(jié)果散布范圍確定樣本數(shù)目成為一個(gè)亟待解決的問題。譚曉慧等[2]通過理論推導(dǎo)和算例分析研究了試驗(yàn)數(shù)量對(duì)可靠指標(biāo)相對(duì)誤差的影響，得出試驗(yàn)數(shù)量增大能減小參數(shù)均值相對(duì)誤差，提高可靠指標(biāo)精度。但研究只考慮了樣本均值的影響而忽略了方差問題。米君楠[3]針對(duì)標(biāo)準(zhǔn)邊坡，通過控制c和φ平均值隨機(jī)生成不同容量的小樣本，研究樣本容量對(duì)破壞概率影響，得出合適的樣本容量為100。但樣本容量過大，在工程實(shí)際中難以操作，同時(shí)沒有針對(duì)參數(shù)變異性進(jìn)行研究。吳振君等[4]針對(duì)只考慮不排水強(qiáng)度的均質(zhì)邊坡，通過可靠度結(jié)果集中程度的直方圖觀察樣本數(shù)目的影響，得出隨參數(shù)變異性增大，樣本數(shù)應(yīng)減少，同時(shí)建議參數(shù)變異系數(shù)在0.2～0.5范圍內(nèi)，樣本數(shù)取10～15。但是計(jì)算模型未考慮φ參數(shù)，以20批次抽樣得到的數(shù)據(jù)容量也較小。因此有待于制定更標(biāo)準(zhǔn)化的方法確定合理樣本數(shù)。針對(duì)普通均質(zhì)邊坡，對(duì)各變異水平下c和φ參數(shù)進(jìn)行不同樣本容量模擬抽樣，重復(fù)抽取120批次構(gòu)建較完備的樣本統(tǒng)計(jì)值空間，基于Fellenius法的Monte-Carlo可靠度分析，形成可靠指標(biāo)計(jì)算結(jié)果空間，根據(jù)不同樣本容量對(duì)結(jié)果離散性的影響，通過控制可靠度指標(biāo)變異程度，探討不同土工參數(shù)變異水平下對(duì)應(yīng)的合理取樣數(shù)目。

1確定最小樣本數(shù)目的傳統(tǒng)參數(shù)估計(jì)法

以樣本信息推斷總體特征的前提是樣本統(tǒng)計(jì)量的抽樣分布。樣本均值的統(tǒng)計(jì)特征為，大樣本時(shí)呈正態(tài)分布，小樣本情況下若方差已知呈正態(tài)分布，反之呈t分布。描述樣本方差的抽樣分布有單個(gè)樣本方差的χ2分布和2個(gè)獨(dú)立樣本方差比的F分布。

1.1樣本均值t分布理論確定最小樣本數(shù)目

小樣本條件下研究樣本數(shù)目與參數(shù)均值估計(jì)誤差關(guān)系一般應(yīng)用t分布區(qū)間估計(jì)理論。高大釗[6]通過大量試算總結(jié)出95%置信水平下，樣本數(shù)目n≥6時(shí)樣本均值相對(duì)誤差可小于3%，滿足實(shí)際工程的精度。由此得到的樣本容量為國內(nèi)建筑邊坡工程技術(shù)規(guī)范[7]及其他土木工程行業(yè)規(guī)范關(guān)于樣本數(shù)目的制定提供了借鑒。董教社等[8]也運(yùn)用t分布理論針對(duì)不同土層不同物理指標(biāo)的實(shí)際變異性系數(shù)提出了合理子樣數(shù)。

根據(jù)t分布函數(shù)，引入反映相對(duì)離散程度變異系數(shù)δ，經(jīng)變換得到樣本均值的相對(duì)誤差Δr算式：

(1)

文獻(xiàn)[10]建議巖土工程中置信水平1-α和容許誤差Δr的取值(見表1)。高大釗等[9-12]總結(jié)出巖土參數(shù)c的變異系數(shù)范圍為0.19～0.55，φ為0.05～0.40。根據(jù)式(1)采用δ=0.2，0.3和0.4，得到t分布理論下不同變異系數(shù)和置信水平對(duì)應(yīng)的最小樣本數(shù)目，見表1。

表1t分布確定的最少樣本數(shù)

Table1Minimumnumberofsamplesaccordingtothetdistribution

相對(duì)誤差置信水平最少樣本數(shù)δ=0.2δ=0.3δ=0.40.100.901326450.100.95183761*0.100.993161*120*

注：n>50時(shí)，t分布用正態(tài)分布近似。加*數(shù)據(jù)為正態(tài)分布計(jì)算。

1.2樣本方差χ2分布理論確定最小樣本數(shù)目

采用t分布理論只能考慮參數(shù)均值因素，但忽略方差問題。應(yīng)用χ2分布理論可研究樣本數(shù)目對(duì)參數(shù)方差估計(jì)誤差產(chǎn)生的影響，經(jīng)χ2函數(shù)變換，樣本方差的相對(duì)誤差為Δr′：

(2)

取與表1相同的置信水平和相對(duì)誤差，根據(jù)式(2)計(jì)算得到χ2分布理論下的最少樣本數(shù)目，如表2所示。

表2χ2分布確定的最小樣本數(shù)

Table2Minimumnumberofsamplesaccordingtotheχ2distribution

置信水平0.900.950.99最少樣本數(shù)117134140

對(duì)比表1和表2可以看出，在相同的置信水平下，若要保證樣本估計(jì)得到的方差具有與均值相同的相對(duì)誤差，需大大增加樣本數(shù)目。

1.3傳統(tǒng)參數(shù)估計(jì)法的不足分析

文獻(xiàn)[13]研究發(fā)現(xiàn)，在標(biāo)準(zhǔn)差相差不大、平均值差異明顯的情況下，數(shù)據(jù)分布曲線形狀大致相同，但曲線中心位置不同，相當(dāng)于將曲線作近似整體平移，導(dǎo)致可靠度分析結(jié)果產(chǎn)生差異。而在標(biāo)準(zhǔn)差差異明顯、平均值差異較小的情況下，數(shù)據(jù)分布曲線的中心位置基本相同而形狀的扁平程度不同，也會(huì)導(dǎo)致可靠度分析結(jié)果產(chǎn)生誤差。因此均值、標(biāo)準(zhǔn)差均對(duì)可靠度計(jì)算結(jié)果產(chǎn)生影響，并且可靠度計(jì)算結(jié)果對(duì)方差比對(duì)均值更加敏感[14]。

以上分別基于t分布和χ2分布理論分析了樣本數(shù)目與參數(shù)均值及與參數(shù)方差的相對(duì)誤差關(guān)系，實(shí)際只分別考慮了樣本均值或方差的估計(jì)而忽略另一統(tǒng)計(jì)參數(shù)問題。更重要的是，這類估計(jì)方法只是停留在分析土工參數(shù)的層面上，并沒有考慮土工參數(shù)(自變量)和可靠度分析結(jié)果(因變量)之間復(fù)雜映射關(guān)系對(duì)取樣數(shù)目造成的影響。同時(shí)計(jì)算出的結(jié)果偏大，實(shí)際中的可操作性不大。

由此需要針對(duì)不同參數(shù)變異性，同時(shí)考慮樣本均值和方差的影響，直接對(duì)由樣本參數(shù)得到的可靠度分析結(jié)果(因變量)進(jìn)行分析，根據(jù)樣本容量對(duì)可靠度指標(biāo)計(jì)算結(jié)果空間散布范圍的約束效應(yīng)，反推出合理樣本數(shù)，體現(xiàn)可靠度分析結(jié)果精度與勘察費(fèi)用間矛盾的協(xié)調(diào)。

2隨機(jī)抽樣分析法及計(jì)算模型

2.1分析思路

工程實(shí)際中，計(jì)算參數(shù)通過容量為n的樣本統(tǒng)計(jì)值得到，由此計(jì)算的可靠度結(jié)果與樣本統(tǒng)計(jì)參數(shù)值為一一對(duì)應(yīng)關(guān)系。在樣本容量較小情況下，若另抽一批次n個(gè)試樣加以統(tǒng)計(jì)，計(jì)算結(jié)果又會(huì)不同，即統(tǒng)計(jì)不確定性造成的結(jié)果離散性。僅容量n足夠大時(shí)，不同批次抽樣的計(jì)算結(jié)果才趨于相等，可靠度真值由土體固有變異性決定，統(tǒng)計(jì)不確定性影響消失。由此，多批次抽樣下樣本數(shù)量與可靠度計(jì)算結(jié)果散布范圍間呈現(xiàn)某種約束關(guān)系，結(jié)果的散布范圍越小則任一批次抽樣計(jì)算的可信度才越高。

分析技術(shù)路線為：1)根據(jù)1.1中已有研究所總結(jié)的土工參數(shù)變異性范圍，劃分出不同變異性水平，通過Matlab生成各變異水平下的參數(shù)總體(數(shù)據(jù)容量為N)，以反映土工參數(shù)固有不確定性；2)給定樣本容量n，以隨機(jī)抽取法模擬一批次勘探取樣，以反映統(tǒng)計(jì)不確定性，并運(yùn)用Fellenius法進(jìn)行Monte-Carlo分析，由樣本統(tǒng)計(jì)值計(jì)算得到對(duì)應(yīng)的一個(gè)可靠度結(jié)果；3)進(jìn)行m批次大量重復(fù)抽取，構(gòu)建數(shù)據(jù)容量均為m的樣本統(tǒng)計(jì)值空間及對(duì)應(yīng)的可靠指標(biāo)計(jì)算結(jié)果空間，使其能包含勘測取樣試驗(yàn)及可靠度計(jì)算結(jié)果的所有可能性；4)變化樣本容量n，得到對(duì)應(yīng)可靠度計(jì)算結(jié)果空間，針對(duì)空間中可靠度指標(biāo)分布的離散性特征展開分析，通過對(duì)比土工參數(shù)變異水平下不同樣本容量對(duì)可靠度結(jié)果的約束效應(yīng)，確定合理樣本數(shù)目。

為提高模擬效率，隨機(jī)抽樣方法采用LHS抽樣(拉丁超立方抽樣)。LHS抽樣是一種分層抽樣方法，合并了隨機(jī)抽樣和分層抽樣的優(yōu)點(diǎn)，是最好的小樣本模擬方法之一[15]。

2.2計(jì)算模型及參數(shù)固有變異性等級(jí)劃分

建立坡高8m，坡比1∶1.5的均質(zhì)邊坡模型，利用對(duì)稱性取1/2邊坡進(jìn)行分析，如圖1所示。以鐵路工程為例，《鐵路地基處理技術(shù)規(guī)程(TB10106-2010)》[16]規(guī)定路堤穩(wěn)定安全系數(shù)Fsk設(shè)計(jì)值為1.25，當(dāng)列車設(shè)計(jì)行車速度處于120km/h與200km/h之間時(shí)，在營運(yùn)期Fsk不得小于1.25。暫以Fsk=1.25為條件進(jìn)行可靠度計(jì)算，其中極限平衡分析方法選用鐵路工程技術(shù)規(guī)范采用的Fellenius法。

圖1　均質(zhì)邊坡模型幾何要素Fig.1 Geometry elements of uniform slope model

變異系數(shù)刻劃了巖土參數(shù)變異性的大致范圍，為便于實(shí)際應(yīng)用，將變異性按變異系數(shù)大小進(jìn)一步劃分出不同水平，有助于定量地細(xì)化評(píng)價(jià)巖土參數(shù)的變異特性。根據(jù)1.1中所述文獻(xiàn)[9～12]，將土工參數(shù)的變異性水平劃分為小、中和大3級(jí)，如表3所列。由于土體容重γ的變異性很小，變異系數(shù)δr<0.1，故不再進(jìn)行等級(jí)劃分，計(jì)算時(shí)按定值考慮。

表3土工參數(shù)變異性水平分級(jí)及計(jì)算取值

Table3Levelofvariationforgeotechnicalparametersandcalculatingvalues

變異水平δφ取值范圍δφ計(jì)算取值δc取值范圍δc計(jì)算取值小變異0.05～0.150.10.20～0.250.2中變異0.15～0.250.20.25～0.350.3大變異0.25～0.400.30.35～0.550.4

2.3土工參數(shù)的樣本統(tǒng)計(jì)值空間構(gòu)建

拉丁超立方抽樣可以避免相同的模擬循環(huán)，同時(shí)保證所有區(qū)間都被抽樣點(diǎn)覆蓋[17]，如圖2所示。利用Matlab軟件中l(wèi)hsnorm(mu,sigma,N)函數(shù)實(shí)現(xiàn)正態(tài)拉丁超立方抽樣，其中mu為參數(shù)均值，sigma代表參數(shù)標(biāo)準(zhǔn)差，N為總體個(gè)數(shù)。

當(dāng)安全系數(shù)Fsk=1.25時(shí)，通過試算得到一組c和φ取值配對(duì)為(10kPa，21.71°)，假設(shè)c和φ服從正態(tài)分布、相互獨(dú)立。容重γ取固定值20kN/m3。變異系數(shù)取值參照表3。參數(shù)總體個(gè)數(shù)取N=5 000。由此可生成大、中和小3種變異水平5 000組參數(shù)總體。

圖2　4×4的Latin方Fig.2 Latin hypercube of 4×4

利用“3σ原則”剔除總體中的無效數(shù)據(jù)。3種變異水平下參數(shù)c和φ相關(guān)系數(shù)分別為0.002 2，0.000 4和0.002 3，可認(rèn)為c和φ相互獨(dú)立。顯著性水平α=0.05下利用K-S檢驗(yàn)[18]分別對(duì)c和φ參數(shù)總體進(jìn)行正態(tài)分布假設(shè)檢驗(yàn)，驗(yàn)證了參數(shù)的分布形態(tài)服從正態(tài)分布。

從生成的呈不同變異水平的5 000對(duì)參數(shù)總體中分別隨機(jī)抽取容量n分別為6，10，15，20，30和50的樣本，并且均重復(fù)抽取m次，由此在不同參數(shù)變異水平和樣本容量條件下得到由m組樣本數(shù)據(jù)構(gòu)成的土工參數(shù)樣本統(tǒng)計(jì)值空間。

2.4重復(fù)抽樣次數(shù)m值的確定

按不同的重復(fù)抽樣次數(shù)計(jì)算參數(shù)均值的相對(duì)誤差，觀察樣本空間大小對(duì)均值相對(duì)誤差的影響。以土工參數(shù)呈大變異水平為例，相對(duì)誤差見表4。

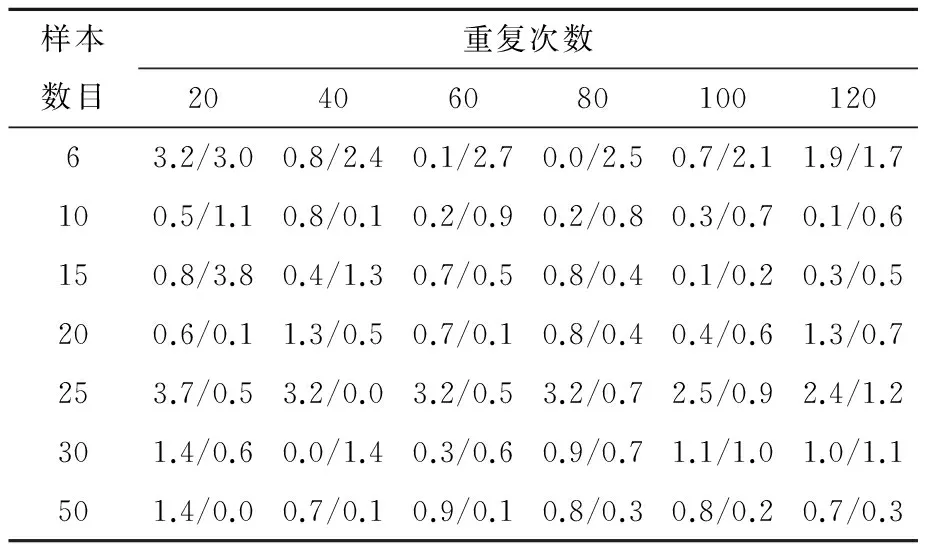
表4　大變異參數(shù)條件下c均值相對(duì)誤差

注：/左、右側(cè)數(shù)據(jù)分別為c值均值相對(duì)誤差和值均值相對(duì)誤差。

由表4可知，不同重復(fù)抽樣次數(shù)得到的參數(shù)均值相對(duì)誤差各異，但是與真值存在較小的誤差，都控制在5%以內(nèi)，是可接受的范圍。

同時(shí)按不同的重復(fù)抽樣次數(shù)計(jì)算參數(shù)標(biāo)準(zhǔn)差，觀察樣本空間大小對(duì)參數(shù)標(biāo)準(zhǔn)差的影響，以土工參數(shù)呈大變異水平為例，如圖3～4所示。

圖3　大變異時(shí)不同抽樣次數(shù)與c標(biāo)準(zhǔn)差關(guān)系Fig.3 Relationship between sampling times and standard deviation of c(large variation level)

圖4　大變異時(shí)不同抽樣次數(shù)與φ標(biāo)準(zhǔn)差關(guān)系Fig.4 Relationship between sampling times and standard deviation ofφ(large variation level)

圖3～4表明，重復(fù)抽樣次數(shù)對(duì)參數(shù)標(biāo)準(zhǔn)差產(chǎn)生較大影響。當(dāng)重復(fù)次數(shù)較少即樣本空間較小時(shí)，由于隨機(jī)抽樣誤差的影響，強(qiáng)度參數(shù)的標(biāo)準(zhǔn)差變化出現(xiàn)大幅度波動(dòng)。當(dāng)抽樣次數(shù)m增加到100～120次時(shí)，標(biāo)準(zhǔn)差趨于穩(wěn)定。

通過不同抽樣次數(shù)條件下均值和標(biāo)準(zhǔn)差的分析，表明抽樣次數(shù)m達(dá)到120次時(shí)構(gòu)建的樣本統(tǒng)計(jì)值空間趨近完備：相對(duì)誤差控制在5%以內(nèi)，標(biāo)準(zhǔn)差趨于穩(wěn)定，即可近似認(rèn)為此時(shí)的抽樣結(jié)果已經(jīng)能包含工程實(shí)際中勘測取樣試驗(yàn)的所有可能性。

2.5樣本統(tǒng)計(jì)值空間特征

圖5　黏聚力c的均值與標(biāo)準(zhǔn)差的散點(diǎn)圖Fig.5 Mean and standard deviation of cohesion

圖6　內(nèi)摩擦角φ的均值與標(biāo)準(zhǔn)差的散點(diǎn)圖Fig.6 Mean and standard deviation of φ

3邊坡可靠度指標(biāo)結(jié)果空間分析

3.1可靠度指標(biāo)結(jié)果空間

在不同的樣本數(shù)目條件下，對(duì)計(jì)算得到的120組可靠指標(biāo)結(jié)果空間數(shù)據(jù)進(jìn)行統(tǒng)計(jì)分析，觀察樣本數(shù)目對(duì)可靠指標(biāo)結(jié)果集中程度的影響。以大變異參數(shù)條件為例，如圖7所示。可以發(fā)現(xiàn)，樣本數(shù)目越大，由多次抽樣數(shù)據(jù)計(jì)算得到的可靠指標(biāo)離散程度越小。

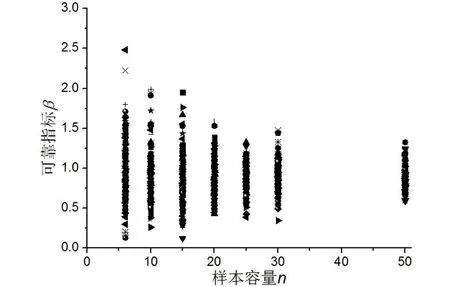
圖7　可靠指標(biāo)散點(diǎn)圖Fig.7 Scatter plot of reliability index

3.2可靠度指標(biāo)的概率分布類型

在顯著性水平α=0.05下用K-S檢驗(yàn)對(duì)可靠指標(biāo)進(jìn)行常用的概型(選取正態(tài)分布、對(duì)數(shù)正態(tài)分布分析)假設(shè)檢驗(yàn)，得出可靠指標(biāo)的最大Dn，與顯著水平0.05上的臨界值Dn0.05進(jìn)行對(duì)比，確定最佳分布類型。若檢驗(yàn)得到Dn小于Dn0.05，則認(rèn)為數(shù)據(jù)服從假設(shè)的分布類型。表5為正態(tài)分布檢驗(yàn)和對(duì)數(shù)分布檢驗(yàn)的結(jié)果。

表5　K-S檢驗(yàn)結(jié)果Dn

注：/左、右側(cè)數(shù)據(jù)分別為正態(tài)分布和對(duì)數(shù)正態(tài)分布檢驗(yàn)結(jié)果。

從假設(shè)分布檢驗(yàn)結(jié)果來看，可靠指標(biāo)服從正態(tài)分布，同時(shí)接受對(duì)數(shù)正態(tài)分布。對(duì)比2種分布檢驗(yàn)結(jié)果，大多數(shù)對(duì)數(shù)正態(tài)分布檢驗(yàn)結(jié)果Dn比正態(tài)分布小，因此可認(rèn)為不同變異水平下可靠指標(biāo)的最佳分布類型為對(duì)數(shù)正態(tài)分布。

4勘察樣本數(shù)目確定

4.1土工參數(shù)變異性與樣本容量影響規(guī)律

在不同的參數(shù)變異水平條件下，統(tǒng)計(jì)各樣本容量對(duì)應(yīng)的可靠指標(biāo)分布的均值與標(biāo)準(zhǔn)差，如圖8～9所示。

圖8　不同樣本容量的β均值Fig.8 Average ofβfor different sample number

圖9　不同樣本容量的β標(biāo)準(zhǔn)差Fig.9 Standard deviation of β for sample number

圖8表明，土工參數(shù)變異性對(duì)可靠指標(biāo)均值影響較大，而樣本容量對(duì)可靠指標(biāo)均值則影響較小。在土工參數(shù)處于小變異情況下邊坡可靠指標(biāo)β均值在2.0～2.5范圍內(nèi)；在中等變異時(shí)，對(duì)應(yīng)的β均值在1.0～1.5范圍內(nèi)；大變異水平時(shí)，β均值在0.5～1.0范圍內(nèi)。不同樣本容量計(jì)算的可靠指標(biāo)均值差異不明顯，接近真實(shí)可靠指標(biāo)。僅在參數(shù)呈小變異，樣本容量為6～15時(shí)，抽樣計(jì)算的可靠指標(biāo)均值與真實(shí)值有較大差異，但相對(duì)誤差也只有10%。而由圖9可知，樣本容量對(duì)可靠指標(biāo)的方差影響顯著。土工參數(shù)變異性一定時(shí)，樣本容量越大，可靠指標(biāo)方差減小，集中程度增大。

4.2基于可靠度離散特征確定樣本數(shù)目

在不同的參數(shù)變異水平條件下，考慮樣本數(shù)目對(duì)可靠指標(biāo)均值和標(biāo)準(zhǔn)差的影響，由各個(gè)樣本容量對(duì)應(yīng)的可靠指標(biāo)均值和標(biāo)準(zhǔn)差計(jì)算得到相應(yīng)的變異系數(shù)，用歸一化的變異系數(shù)反映可靠度分析結(jié)果的離散程度，見圖10。

圖10　不同樣本容量的β變異系數(shù)Fig.10 Variation coefficient of β for sample number

圖10表明，樣本數(shù)目增加可減小可靠指標(biāo)分布的離散程度，但土工參數(shù)變異性增大則會(huì)增大可靠指標(biāo)分布的離散程度。樣本數(shù)為10時(shí)，小變異水平的土工參數(shù)對(duì)應(yīng)結(jié)果的變異性只有0.23，而土工參數(shù)變異性增大到中、大變異水平時(shí)，結(jié)果變異性增加至0.31和0.38，離散程度增大；當(dāng)樣本數(shù)由10增大到50時(shí)，小、中和大變異水平的參數(shù)對(duì)應(yīng)結(jié)果的變異系數(shù)降至0.1，0.15和0.17，離散程度大大降低。由此，為保證可靠度分析結(jié)果精度，在土工參數(shù)變異性增大條件下須相應(yīng)增加樣本數(shù)目。

由可靠指標(biāo)變異性隨樣本容量變化的趨勢推斷，只有在樣本容量足夠大時(shí)，才能得到不同土工參數(shù)變異水平對(duì)應(yīng)結(jié)果的精確解。然而，樣本容量的確定不能只滿足結(jié)果精度要求，同時(shí)也要符合工程實(shí)際中取樣有限的特點(diǎn)。因此合理樣本數(shù)目的選取需要協(xié)調(diào)結(jié)果精度與勘察費(fèi)用的矛盾，在控制結(jié)果精度在一定范圍的同時(shí)，又不造成勘察費(fèi)用的浪費(fèi)。

控制結(jié)果變異系數(shù)為0.30，0.25和0.20，由圖10確定各個(gè)變異水平等級(jí)的參數(shù)對(duì)應(yīng)的樣本數(shù)。如表6所示。

表6不同變異水平等級(jí)的土工參數(shù)對(duì)應(yīng)的樣本數(shù)

Table6Numberofsamplecorrespondingtothedifferentlevelsofsoilparameters

可靠指標(biāo)變異系數(shù)小變異中變異大變異0.30611180.25915200.20152030

5結(jié)論

1)物理不確定性是天然存在的，主要影響可靠度真值大小。統(tǒng)計(jì)不確定性是由于小樣本取樣試驗(yàn)人為造成的，影響可靠度分析結(jié)果圍繞真值的離散程度。減小統(tǒng)計(jì)不確定性是提高可靠度分析結(jié)果精度的關(guān)鍵。

2)樣本數(shù)目對(duì)可靠度分析結(jié)果離散程度影響顯著。土工參數(shù)變異性不變時(shí)，樣本數(shù)目增多，結(jié)果的離散程度降低；參數(shù)變異性增大，若結(jié)果達(dá)到與小變異性下相同的離散程度，則所需樣本數(shù)增大。

3)確定了土工參數(shù)在不同變異水平下，可靠指標(biāo)變異系數(shù)取0.30，0.25和0.20時(shí)對(duì)應(yīng)的樣本數(shù)目。參數(shù)呈小變異水平時(shí)，對(duì)應(yīng)樣本數(shù)為6，9和15，中、大變異水平時(shí)樣本數(shù)目宜分別提高為11，15和20及18，20和30。研究成果對(duì)完善工程勘察中的土工試驗(yàn)取樣數(shù)目有促進(jìn)作用。

參考文獻(xiàn)：

[1] 冷伍明，趙善銳.土工參數(shù)不確定性的計(jì)算分析[J].巖土工程學(xué)報(bào), 1995, 17(2):68-74.

LENGWuming，ZHAOShanrui.Analysisontheuncertaintiesofsoilproperties[J].ChineseJournalofGeotechnicalEngineering, 1995, 17(2):68-74.

[2] 譚曉慧，王建國，馮敏杰.巖土工程中試驗(yàn)數(shù)量與可靠指標(biāo)的關(guān)系[J].中國科學(xué)技術(shù)大學(xué)學(xué)報(bào), 2008, 38(11):1326-1331.

TANXiaohui,WANGJianguo,FENGMinjie.Relationshipbetweennumberoftestsamplesandreliabilityindexingeotechnicalengineering[J].JournalofUniversityofScienceandTechnologyofChina, 2008, 38(11):1326-1331.

[3] 米君楠.參數(shù)變異性及樣本容量對(duì)邊坡可靠度影響的研究[D].杭州：浙江大學(xué)，2007.

MIJunnan.Studyonvariabilityofsoilparametersandsamplesizeinreliabilityanalysisofslope[D].Hangzhou:ZhengjiangUniwersity, 2007.

[4] 吳振君,湯華,王水林,等.巖土樣本數(shù)目對(duì)邊坡可靠度分析的影響研究[J].巖土力學(xué)與工程學(xué)報(bào), 2013, 32(增1):2346-2854.

WUZhenjun,TANGhua,WANGShuilin.Influenceofnumberofgeotechnicalsamplesonslopereliabilityanalysis[J].ChineseJournalofRockMechanicsEngineering, 2013, 32(Suppl1): 2346-2854.

[5] 錢家歡,殷宗澤.土工原理與計(jì)算[M]. 北京：中國水利水電出版社，1996.

QIANJiahuan,YINZongze.Earthworktheoryandcalculation[M].Beijing:ChinaWater&PowerPress, 1996.

[6] 高大釗.關(guān)于巖土設(shè)計(jì)參數(shù)標(biāo)準(zhǔn)值計(jì)算公式的討論[J].工程勘察, 1996(3):5-8.

GAODazhao.Discussionabouttheformulaofparameterstandardvaluesingeotechnicaldesign[J].EngineeringInvestigation, 1996(3):5-8.

[7]GB50330—2013,建筑邊坡工程技術(shù)規(guī)范[S].

GB50330—2002,Technicalcodeforbuildingslopeengineering[S].

[8] 董教社，成利民.巖土工程勘察中合理子樣數(shù)的探討[J].港工技術(shù), 1999(2):52-54.

DONGJiaoshe,CHENGLimin.Discussionaboutreasonablenumberofsamplesingeotechnicaldesign[J].PortEngineeringTechnology, 1999(2):52-54.

[9] 高大釗.土力學(xué)可靠性原理[M]. 北京：中國建筑工業(yè)出版社，1989.

GAODazhao.Theprincipleofthereliabilityofsoilmechanics[M].Beijing:ChinaArchitecture&BuildingPress, 1989.

[10]DuncanJM.Factorsofsafetyandreliabilityingeotechnicalengineering[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 2000, 126(4):307-316.

[11] 張繼周,繆林昌,劉峰.巖土參數(shù)的不確定性及其統(tǒng)計(jì)方法[J].巖土力學(xué), 2008, 28(增):495-499.

ZHANGJizhou,MIAOLinchang,LIUFeng.Uncertaintiesofsoilpropertiesanditsstatisticalmethod[J].RockandSoilMechanics,2008, 28(Suppl):495-499.

[12] 李小勇.土工參數(shù)空間概率特征[M]. 北京：原子能出版社，2006.

LIXiaoyong.Thespatialprobabilisticcharacteristicsofgeotechnicalparameters[M].Beijing:AtomicEnergyPress, 2006.

[13] 吳興正，蔣良濰，羅強(qiáng),等. 路堤邊坡穩(wěn)定可靠度計(jì)算中的模型不確定性分析[J]. 巖土力學(xué), 2015, 36(增2):665-672.

WUXingzheng,JIANBGLiangwei,LUOqiang,etal.Analysisofmodeluncertaintyforstabilityreliabilityofembankmentslope[J].RockandSoilMechanics,2008, 36(Suppl2):665-672.

[14] 李亮,張丙強(qiáng).c,φ相關(guān)性對(duì)邊坡整體穩(wěn)定性的影響[J].鐵道科學(xué)與工程學(xué)報(bào),2004, 1(1):62-68.

LILiang,ZHANGBingqiang.Influenceofcorrelationsofcandφonslopestability[J].JournalofRailwayScienceandEngineering, 2004, 1(1): 62-68.

[15] 萬越,呂震宙,袁修開.基于Latin方抽樣和修正的方抽樣的可靠性靈敏度估計(jì)及其方差分析[J].機(jī)械強(qiáng)度, 2008, 30(6):927-934.

WANYue,LüZhenzhou,YUANXiukai.Latinhypercubesamplingandupdatedlatinhypercubesamplingmethodforreliabilitysensitivityanditsvarianceanalysis[J].JournalofMechanicalStrength, 2008, 30(6):927-934.

[16]TB10106—2010，鐵路工程地基處理技術(shù)規(guī)程[S].

TB10106—2010,Technicalcodeforgroundtreatmentofrailwayengineering[S].

[17] 郝中軍,扈曉翔.基于拉丁超立方抽樣的導(dǎo)彈快速精度分析與誤差補(bǔ)償方法[J].兵工自動(dòng)化, 2009, 28(6):23-25.

HAOZhongjun,HUXiaoxiang.Errorcompe-nsationmethodandrapidaccuracyanalysisformissilebasedonlatinhypercubesampling[J].OrdnanceIndustryAutomation, 2009, 28(6):23-25.

[18] 祝玉學(xué).邊坡可靠性分析[M]. 北京：冶金工業(yè)出版社，1993.

ZHUYuxue.Reliabilityanalysisofslope[M].Beijing:MetallurgicalIndustryPress, 1993.

* 收稿日期：2015-09-09

基金項(xiàng)目：國家重點(diǎn)基礎(chǔ)研究發(fā)展計(jì)劃(973計(jì)劃)項(xiàng)目(2013CB036204)；中央高校基本科研業(yè)務(wù)費(fèi)專項(xiàng)資金資助項(xiàng)目(2682014CX064)

通訊作者：蔣良濰(1974-)，男，四川成都人，副教授，博士，從事路堤邊坡可靠度的研究；E-mail: 154999419@qq.com

中圖分類號(hào)：U213.1

文獻(xiàn)標(biāo)志碼：A

文章編號(hào)：1672-7029(2016)06-1053-08

Study on the geotechnical number of samples in slope reliability analysis

ZHAO Jing1,2，JIANG Liangwei1,2，LUO Qiang1,2，LUO Fei1,2，KONG Dehui1,2

(1.SchoolofCivilEngineeringSouthwestJiaotongUniversity，Chengdu610031，China;2.MOEKeyLaboratoryofHigh-speedRailwayEngineering，SouthwestJiaotongUniversity，Chengdu610031，China)

Abstract:Soil parameters were estimated by the survey test of limited sample number and its statistical uncertainty would lead to the error of reliability analysis. Thus a number of samples should be considered in terms of survey cost and precision. Based on the method of random sampling from the total soil parameters to simulate the survey under certain sample number, the sample statistical value and the discrete features of slope reliability index correspondingly are analyzed with 120 times sampling. Based on the influence of sample number on discrete features of slope reliability index, the number of sample corresponding to three levels of soil parameters is discussed. The analysis result shows that the increased number of samples would lead to the small dispersion degree of reliability index, and the increasing variability of parameters would tead to the opposite result. In order to ensure the accuracy of the results, the number of sample should increase with the increase of reliability index of soil parameters. According to small, medium and large variation levels of soil parameters, the required number of samples are found to be 6, 11 and 18 seperately when the coefficient of variation is 0.30. Research provides reference on the soil test of engineering survey.

Key words：slope reliability analysis; number of samples; statistical uncertainty; reliability index; discrete range; coefficient of variation; random sample