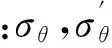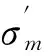考慮孔隙水壓劣化作用的圍巖黏彈性變形解

俞凱木，俞縉,2，周雨晴

(1. 華僑大學 巖土工程研究所，福建 廈門 361021；2. 中國礦業大學 深部巖土力學與地下工程國家重點實驗室，江蘇 徐州 221008)

?

考慮孔隙水壓劣化作用的圍巖黏彈性變形解

俞凱木1，俞縉1,2，周雨晴1

(1. 華僑大學 巖土工程研究所，福建 廈門 361021；2. 中國礦業大學 深部巖土力學與地下工程國家重點實驗室，江蘇 徐州 221008)

摘要:基于Terzaghi 有效應力原理，建立孔隙水壓作用下軸對稱隧洞的平衡方程，利用平面應變理論計算彈性應力場，并在體積應變率保持不變下獲得高孔隙水壓劣化Kelvin流變圍巖的黏彈性蠕變解。在對比Gu解基礎上，對不同孔隙水壓與水頭邊界進行敏感性分析，結果表明：隨著孔隙水壓增大，蠕變穩定階段逐漸向不穩定發展，尤其在高孔隙水壓作用下圍巖劣化變形能力明顯增大，印證了佘成學等人的試驗成果；當內外水壓比較小時，洞壁時效變形發展較快，蠕變衰減階段持續時間較長。該研究可為分析高孔隙水壓作用下深埋隧洞圍巖劣化的黏彈性變形提供理論基礎。

關鍵詞：孔隙水壓；平衡方程；黏彈性蠕變；圍巖劣化；彈性應力

在高孔隙水壓作用下，巖石的強度由于圍壓被抵消而降低，其承載時間逐漸縮短，變形能力明顯增大[1-3]。試驗研究表明[4]，隨著孔隙水壓增大，高圍壓下Kelvin流變巖體的黏彈性模量顯著線性遞減。因此，深埋巖體隧洞在高孔隙水壓作用下巖體質量不斷劣化，其強度和變形剛度逐漸衰減，變形能力逐步增大。近年來，隨著礦山開采工程、水利水電工程向深部發展[5]，高地應力與高孔隙水壓條件下隧洞長期變形與穩定問題日益突出，高孔隙水壓劣化作用下圍巖時效變形研究尚處于探索階段。針對孔隙水壓對圍巖時效變形影響的解析研究，魏佳等[6]建立了含有孔隙水壓的Burgers體蠕變數學模型，從理論上說明了隧洞圍巖的孔隙水壓是影響其穩定性的重要因素。梁冰等[7]考慮了孔隙水壓及孔隙度在蠕變過程中對于巖體變形的影響，提供了探索孔隙水壓對圍巖蠕變影響的數學方法，但其平衡方程與彈性應力分布均不計入孔隙水壓影響，與實際不符。Dufour等[8]利用Kevin-Voigt蠕變模型，采用Laplace變換計算了黏彈性流變隧洞壽命終止后回填階段的三維應力位移分布(考慮中主應力影響)，但在計算隧洞開挖、孔壓消散等階段的應力位移響應時，忽略了巖體蠕變[9]。LE等[10]建立了一種考慮時間效應的水力耦合數值模型，說明了泥巖各向異性蠕變對巖體隧洞水力耦合效應的重要影響。GU等[11-12]基于改進的Burgers模型計算了滲流作用下圍巖黏彈塑性蠕變行為。這些研究為孔隙水壓作用下圍巖時效力學行為的分析建立了理論基礎，但均沒有考慮到孔隙水壓對圍巖力學參數的劣化影響以及由之產生的時效變形響應。從現場實測與試驗研究可知[1-4]，探討高孔隙水壓作用下深埋隧洞劣化圍巖的時效變形具有重要意義。本文基于Terzaghi 有效應力原理，建立孔隙水壓作用下軸對稱隧洞的平衡方程，基于平面應變理論計算深埋隧洞彈性應力解，并獲得高孔隙水壓作用下Kelvin流變巖體隧洞在圍巖力學參數(黏彈性模量)劣化情況下的黏彈性蠕變解。以期為分析高孔隙水壓作用下深埋圓形隧洞劣化圍巖的黏彈性變形提供數理力學理論基礎。

1考慮孔隙水壓作用的圍巖應力場

1.1考慮孔隙水壓影響的平衡方程

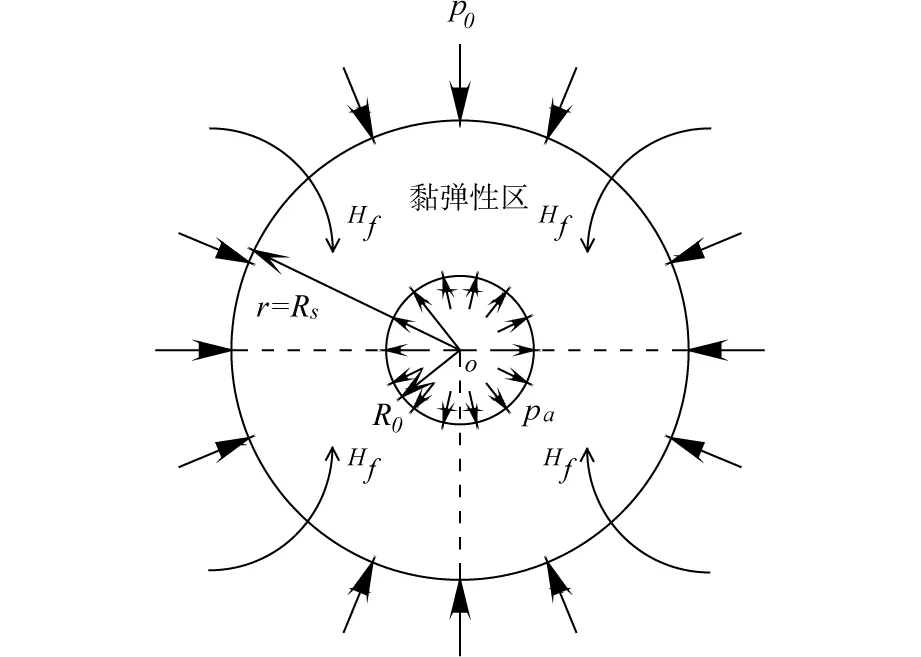
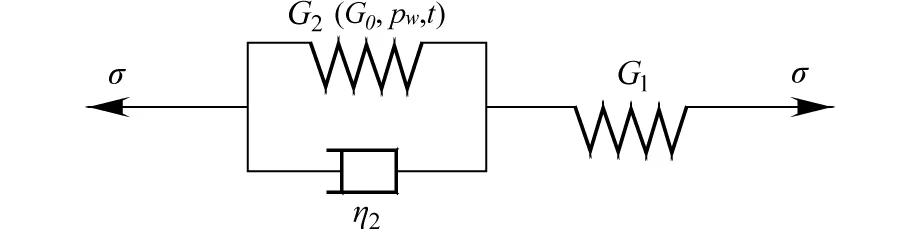
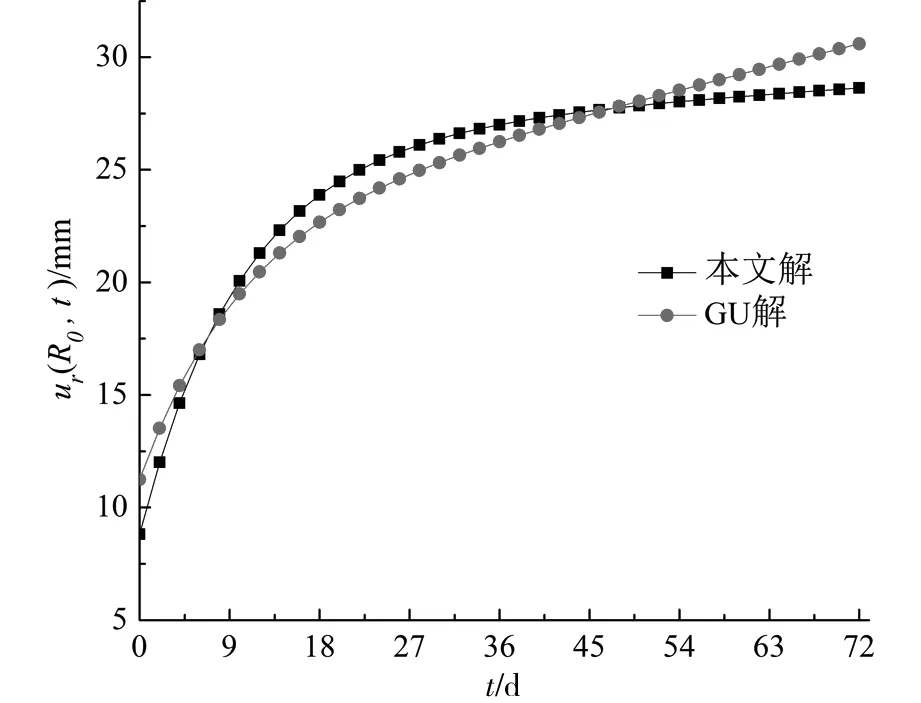
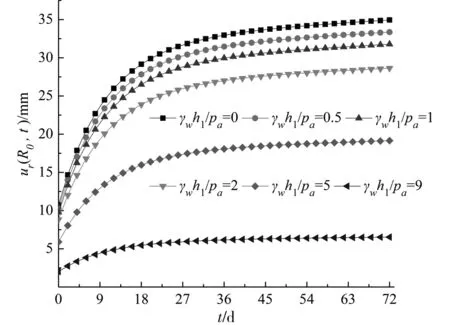
如圖1所示，R0為隧洞半徑；Rs為滲流響應區半徑或者圍巖回彈區半徑，在R0

平面應變條件下軸對稱隧洞的平衡方程[13]：

(1)

根據Terzaghi 有效應力原理：

(2)

圖1　隧洞力學模型Fig.1 Tunnel mechanics model

將式(2)代入式(1)，可得

(3)

式中:孔壓梯度dpw(r)/dr一般被視為滲流力[14～15]。根據文獻[14]，可知

(4)

根據文獻[16]，定義Hf為滲流因子，如圖1所示。結合式(3)，可得孔隙水壓影響下平衡方程。對比基于體力理論的平衡方程[17]，可發現當Rs=αR0(α取值足夠大)時兩者一致。據此，對照李宗利等[17]成果可佐證本文獲得的彈性應力解。

1.2考慮孔隙水壓影響的彈性應力分布

用位移分量表示應力分量的Hooke定律為：

(5)

式中:u為徑向位移；E和μ分別為圍巖彈性模量和泊松比。

將式(5)代入(3)，可得：

(6)

可得式(6)通解：

(7)

將式(7)代入式(5)，可得：

(8)

積分常數可通過如下應力邊界條件求得：

(9)

將式(9)代入式(8)，可得積分常數：

(10)

將式(10)代入式(8)，則考慮孔隙水壓影響的深埋隧洞彈性應力場如下：

(11)

(12)

深埋隧洞圍巖受力與變形是復雜的三維問題，根據文獻[18]，有

(13)

據此，可獲得孔隙水壓作用下深埋隧洞彈性應力場。當Rs=αR0時，文中計算結果與文獻[17]一致。

2孔隙水壓劣化圍巖黏彈性蠕變計算

在高孔隙水壓作用下巖體質量不斷劣化，其強度和變形剛度逐漸衰減，隧洞變形能力逐步增大。蔣海飛等[4]基于高圍壓下不同孔隙水壓作用時的蠕變試驗結果，發現高圍壓下Kelvin流變巖體的黏彈性模量隨孔隙水壓增大呈線性遞減關系，并提出一個修正的廣義Kelvin模型(如圖2所示)。該模型的三維蠕變方程為：

(14)

式中:Sij為偏應力；G1為Hooke體黏彈性剪切模量；η2為Kelvin體黏滯系數；G2(G0,pw,t)為劣化黏彈性剪切模量，且G2(G0,pw,t)=G0+βt-atbpw，a，b和β為線性遞減關系中的擬合參數。可知G2為初始黏彈性剪切模量G0，孔隙水壓pw以及時間t的多元函數，亦為孔隙水壓pw的線性遞減函數。該函數建立了初始時刻與后續時刻黏彈性剪切模量之間的關系，能夠反映材料特性隨孔隙水壓與時間的劣變過程。

圖2　修正廣義Kelvin 模型Fig.2 Modified Kelvin model

深埋巖體隧洞變形幾何方程為：

ur(r,t)=∫εr(r,t)dr

(15)

ur(r,t)=εθ(r,t)r

(16)

在求解該問題時，式(15)～(16)必須同時滿足；但以往為了簡化求解，只考慮其中一個幾何方程，如Fahimifar解[19]，該解法在幾何上并不嚴謹。為客觀獲取徑向位移解答，假設在黏性響應中，體積應變率保持不變[20]，則

(17)

其中，

(18)

將式(18)代入式(17)，可得

(19)

由此可得帶積分常數J的通解：

(20)

對式(14)、式(20)分別求微分，可得：

(21)

進一步可得積分常數J：

(22)

(23)

當不考慮時間效應時，孔隙水壓劣化圍巖黏彈性蠕變解將退化為隧洞開挖瞬時解，根據文獻[17]，可取邊界條件：

(24)

將彈性應力場代入式(23)，并代入(20)，借助邊界條件(24)可得廣義Kelvin流變巖體隧洞在孔隙水壓作用下劣化圍巖的黏彈性蠕變場：

(25)

3討論分析

下面對前述考慮高孔隙水壓劣化的深埋圓形隧洞圍巖黏彈性蠕變解進行計算討論分析。在參數確定過程中，為了模擬高地應力與高孔隙水壓條件，參考文獻[17,18]，選取參數p0=30 MPa，pa= 4.9 MPa(等價于500 m水頭)。以pa為基準，內外水壓比γwh1/pa分別為0，0.5，1，2，5和9。取R0=3 m，μ=0.25，Rs=90 m，γw=9.8 kN/m3，a=0.5，b=0.8，β=-0.03。另外，根據FENG等[21]的研究成果，廣義Kelvin模型的蠕變參數選用G0=1 000 MPa，G1=2 000 MPa，η2=10 000 MPa·D。

圖3為本文計算結果與GU解[11]的對比。從圖3可知，2種計算結果均能體現黏彈性流變巖體的蠕變特性，且吻合度較高。主要區別在于蠕變第2階段的蠕變率，對比基于Burgers模型的GU解[11]，基于廣義Kelvin模型的本文解蠕變率較小。這里給出2種解釋，一是由于蠕變模型不同所致，可見正確辨識巖體在受力狀態下的蠕變行為至關重要；二是由于黏彈性剪切模量劣化所致，使2種不同模型下的蠕變行為偏離更厲害。

圖3　洞壁黏彈性蠕變曲線對比Fig.3 Comparision of viscoelastic creep curves

圖4　不同pw下洞壁黏彈性蠕變曲線Fig.4 Viscoelastic creep curve under different pw

圖4為不同pw下洞壁黏彈性蠕變曲線。隨著孔隙水壓增大，洞壁蠕變第2階段逐漸由穩定向不穩定發展；當pw=15 MPa時，即高孔隙水壓作用下隧洞變形能力明顯增大，并有可能促使圍巖受力進入塑性狀態直至加速破壞。增大孔隙水壓，深埋Kelvin流變巖體的黏彈性模量顯著降低，促使相同應力水平下圍巖變形增大，印證了佘成學等的研究成果。

根據式(4)～(5)可知，內外水壓比γwh1/pa是孔隙水壓分布的影響因素；由于γwh1/pa比值反映了滲流方向[16,22-23](當γwh1/pa<1時，滲流方向為洞外指向洞內，會加劇洞壁位移；當γwh1/pa>1時，滲流方向為洞內指向洞外，會減小洞壁位移；γwh1/pa=1時，則滲流不發生)，因此有必要對該因素展開敏感性分析。

圖5　不同γwh1/pa下洞壁黏彈性蠕變曲線Fig.5 Viscoelastic creep curve under different γwh1/pa

圖6為不同γwh1/pa下洞壁黏彈性蠕變曲線，初始階段蠕變速度相對較快，隨后曲線趨于平緩，能充分體現Kelvin流變巖體的黏彈性蠕變特性。當γwh1/pa較小時，洞壁時效變形發展較快，衰減蠕變直至穩定蠕變所持續的時間較長。隨γwh1/pa增大，曲線趨于平緩，變形量也相應減少。

4結論

1)隨著孔隙水壓增大，蠕變穩定階段逐漸向不穩定發展，尤其在高孔隙水壓作用下劣化圍巖變形能力明顯增大；

2)當內外水壓比γwh1/pa較小時，洞壁時效變形發展較快，蠕變衰減階段持續時間較長；

3)高孔隙水壓劣化圍巖，導致巖體強度和變形剛度雙重衰減，深埋巖體隧洞極有可能發生強度破壞以及與時間相關的黏彈塑性大變形。文中只初步解析黏彈性流變問題，對高孔隙水壓劣化圍巖機制以及相關工程失效問題將在后續研究中深入討論。

參考文獻：

[1] 佘成學，崔旋. 高孔隙水壓力對巖石蠕變特性的影響[J] 巖石力學與工程學報，2010，29(8)：1603-1609.

SHEChengxue,CUIXuan.Influenceofhighporewaterpressureoncreeppropertiesofrock[J].ChineseJournalofRockMechanicsandEngineering, 2010, 29(8): 1603-1609.

[2] 蔣海飛，劉東燕，黃偉，等. 高圍壓下高孔隙水壓對巖石蠕變特性的影響[J]. 煤炭學報，2014，39(7)：1248-1256.

JIANGHaifei,LIUDongyan,HUANGWei,etal．Influenceofhighporewaterpressureoncreeppropertiesofrockunderhighconfiningpres-sure[J]．JournalofChinaCoalSociety, 2014, 39(7): 1248-1256．

[3] 黃書嶺，馮夏庭，周 輝，等. 水壓和應力耦合下脆性巖石蠕變與破壞時效機制研究[J]. 巖土力學，2010，31(11)：3441-3446.

HUANGShuling,FENGXiating,ZHOUHui,etal.Studyofagingfailuremechanicsandtriaxialcompressioncreepexperimentswithwaterpressurecoupledstressofbrittlerock[J].RockandSoilMechanics, 2010, 31(11): 3441-3446.

[4] 蔣海飛，劉東燕，黃偉，等. 高圍壓下不同孔隙水壓作用時巖石蠕變特性及改進西原模型[J]. 巖土工程學報，2014，36(3)：443-451.

JIANGHaifei，LIUDongyan，HUANGWei，etal．CreeppropertiesofrockunderhighconfiningpressureanddifferentporewaterpressuresandamodifiedNishiharamodel[J].ChineseJournalofGeotechnicalEngineering, 2014, 36(3): 443-451.

[5] 蔡美峰，何滿潮，劉東燕．巖石力學與工程[M]．北京: 科學出版社，2009：307-308．

CAIMeifeng,HEManchao,LIUDongyan.Rockmechanicsandengineering[M].Beijing:SciencePress, 2009: 307-308．

[6] 魏佳，李劍光，段雪娣. 孔隙水壓對巖體蠕變影響研究[J]. 礦山壓力與頂板管理，2006，22(4)：125-126.

WEIJia,LIJianguang,DUANXuedi.Studyoneffectofporouspressuretononlinearcreepofdeeprocks[J].GroundPressureandStrataControl, 2006, 22(4): 125-126.

[7] 梁冰，李平. 孔隙壓力作用下圓形巷道圍巖的蠕變分析[J]. 力學與實踐，2006，28(5)：69-72.

LIANGBing,LIPing.Creepanalysisofrocksurroundingroundtunnelbyconsideringporepressure[J].MechanicsinEngineering, 2006, 28(5): 69-72.

[8]DufourN,LeoCJ,DeleruyelleF,etal.Hydromechanicalresponsesofadecommissionedbackfilledtunneldrilledintoaporo-viscoelasticmedium[J].SoilsandFoundations, 2009, 49(4): 495-507.

[9]DufourN,WongH,DeleruyelleF,etal.HydromechanicalPostclosureBehaviorofaDeepTunnelTakingintoAccountaSimplifiedLifeCycle[J].InternationalJournalofGeomechanics, 2011, 12(5): 549-559.

[10]LeAD,NguyenTS.Hydromechanicalresponseofabeddedargillaceousrockformationtoexcavationandwaterinjection1[J].CanadianGeotechnicalJournal, 2014, 52(1): 1-17.

[11]GUXB,YANL.Visco-elasto-plasticcreepsolutionstocirculartunnelsconsideringseepageforce[J].ElectronicJournalofGeotechnicalEngineering, 2013, 18: 2231-2241.

[12]XUJ,GUXB.Viscoelasticcreepsolutionstocirculartunnelsconsideringwaterpressure[J].ElectronicJournalofGeotechnicalEngineering, 2014, 19: 1493-1501.

[13]Carranza-TorresC,ZHAOJ.Analyticalandnumericalstudyoftheeffectofwaterpressureonthemechanicalresponseofcylindricallinedtunnelsinelasticandelasto-plasticporousmedia[J].InternationalJournalofRockMechanicsandMiningSciences, 2009, 46(3): 531-547.

[14]FahimiearA,ZareifardMR.Atheoreticalsolutionforanalysisoftunnelsbelowgroundwaterconsideringthehydraulic-mechanicalcoupling[J].TunnellingandUndergroundSpaceTechnology, 2009, 24(6): 634-646.

[15]ZareifardMR,FahimifarA.EffectofseepageforcesoncircularopeningsexcavatedinHoek-Brownrockmassbasedonageneralisedeffectivestressprinciple[J].EuropeanJournalofEnvironmentalandCivilEngineering, 2014, 18(5): 584-600.

[16] 張建智，俞縉，蔡燕燕，等. 滲水膨脹巖隧洞黏彈塑性蠕變解及變形特性分析[J]. 巖土工程學報，2014，36(12)：2195-2202.

ZHANGJianzhi,YUJin,CAIYanyan,etal.Viscoelastic-plasticcreepsolutionsanddeformationpropertiesoftunnelsinswellingrocksunderseepage[J].ChineseJournalofGeotechnicalEngineering, 2014, 36(12): 2195-2202.

[17] 李宗利，任青文，王亞紅. 考慮滲流場影響深埋圓形隧洞的彈塑性解[J]. 巖石力學與工程學報，2004，23(8)： 1291-1295.

LIZongli,RENQingwen,WANGYahong.Elasto-plasticanalyticalsolutionofdeep-buriedcircletunnelconsideringfluidflowfield[J].ChineseJournalofRockMechanicsandEngineering, 2004, 23(8): 1291-1295.

[18] 侯公羽，牛曉松. 基于Levy-Mises本構關系及D-P屈服準則的軸對稱圓巷理想彈塑性解[J]. 巖土力學，2009，30(6)：1555-1562.

HOUGongyu,NIUXiaosong.PerfectelastoplasticsolutionofaxisymmetriccircularopeningsinrockmassbasedonLevy-MisesconstitutiverelationandD-Pyieldcriterion[J].RockandSoilMechanics, 2009, 30(6): 1555-1562.

[19]FahimifarA,ThraniFM,HedayatA,etal.Analyticalsolutionfortheexcavationofcirculartunnelsinavisco-elasticBurger’smaterialunderhydrostaticstressfield[J].TunnellingandUndergroundSpaceTechnology, 2010, 25(4): 297-304.

[20] 王者超，陳衛忠，喬麗蘋，等. 地下工程應力松弛效應的初步理論解[J]. 巖石力學與工程學報，2010，29(增2)：4096-4101.

WANGZhechao,CHENWeizhong,QIAOLiping,etal．Preliminarystudyoftheoreticalsolutiontostressrelaxationeffectforundergroundengineering[J].ChineseJournalofRockMechanicsandEngineering, 2010, 29(Suppl2): 4096-4101.

[21]FENGXT,CHENBR,YANGC,etal.Identificationofvisco-elasticmodelsforrocksusinggeneticprogrammingcoupledwiththemodifiedparticleswarmoptimizationalgorithm[J].InternationalJournalofRockMechanicsandMiningSciences, 2006, 43:789-801.

[22]YUJ,LIT,ZHANGJ,CAIYanyan.Stresscharacteristicsofsurroundingrocksforinnerwaterexosmosisinhigh-pressurehydraulictunnels[J].JournalofCentralSouthUniversity, 2014, 21: 2970-2976.

[23] 蔡燕燕，張建智，俞縉，等. 近溶腔高壓水工隧洞圍巖應力位移彈性解[J]. 現代隧道技術，2015，52(1)：45-54.

CAIYanyan,ZHANGJianzhi,YUJin,etal．Elasticsolutionofrockstressanddisplacementinahigh-pressurehydraulictunneladjacenttoaKarstcavity[J].ModernTunnellingTechnology, 2015, 52(1): 45-54.

* 收稿日期：2015-07-15

基金項目：國家自然科學基金資助項目(51374112)；福建省自然科學基金資助項目(2014J 01160)；中國礦業大學深部巖土力學與地下工程國家重點實驗室開放基金項目(SKLGDUEK1304)

通訊作者：俞縉(1978-)，男，江蘇南京人，教授，博士，從事巖石力學及地下工程方面的研究；E-mail: bugyu0717@hqu.edu.cn

中圖分類號：U451.2

文獻標志碼：A

文章編號：1672-7029(2016)06-1046-07

Viscoelastic deformation solution of surrounding rock within deteriorated effect of pore water pressure

YU Kaimu1，YU Jin1,2，ZHOU Yuqing1

(1.Geotechnical Engineering Institute，Huaqiao University，Xiamen 361021，China；2. State Key Laboratory for Geomechanics and Deep Underground Engineering，China University of Mining and Technology，Xuzhou 221008，China)

Abstract:Equilibrium equations about axial symmetrical tunnel under pore water pressure have been established based on the Terzaghi effective stress principle. The elastic stress generalized function solution about deep buried tunnels has been calculated using the plane strain theory. Viscoelastic creep solution of deteriorated and Kelvin rheological rock under high pore water pressure has been acquired while the volumetric strain rate remains constant. Sensitivity analysis of various pore water pressures and boundary conditions has been performed based on the comparison between solutions of Gu. The results show that with the increase of pore water pressure, the creep stage change from stable to unstable condition. The deformation capacity of deteriorated rock increases obviously, especially under the action of high pore water pressure. This finding agrees with the test results of Chengxue She. When the inner/outer water pressure ratio is relatively small, the deformation of tunnels’ wall develops rapidly. It has been a long time until decay creep become stable. This study can provide a theoretical basis for the analysis of the deteriorated rock’s viscoelastic deformation of deep buried tunnels under high pore water pressure.

Key words：pore water pressure; equilibrium equation; viscoelastic creep; deteriorated rock; elastic stress