基于分布式低秩表示的子空間聚類算法

許　凱　吳小俊　尹賀峰

(江南大學物聯網工程學院　江蘇無錫　214122)

?

基于分布式低秩表示的子空間聚類算法

許凱吳小俊尹賀峰

(江南大學物聯網工程學院江蘇無錫214122)

(xukai347@sina.com)

摘要針對基于低秩表示的子空間分割算法運算時間較長、聚類的準確率也不夠高，提出一種基于分布式低秩表示的稀疏子空間聚類算法(distributed low rank representation-based sparse subspace clustering algorithm, DLRRS)，該算法采用分布式并行計算來得到低秩表示的系數矩陣，然后保留系數矩陣每列的前k個絕對值最大系數，其他系數置為0，用此系數矩陣構造一個稀疏的樣本關系更突出的相似度矩陣，接著用譜聚類得到聚類結果.但是其不具備增量學習功能，為此再提出一種基于分布式低秩表示的增量式稀疏子空間聚類算法(scalable distributed low rank representation based sparse subspace clustering algorithm, SDLRRS)，如果有新增樣本，可以利用前面的聚類結果對新增樣本進行分類得到最后的結果.實驗結果表明:所提2種子空間聚類算法不僅有效減少算法的運算時間，還提高了聚類的準確率，從而驗證算法是有效可行的.

關鍵詞低秩表示；子空間聚類；并行計算；增量學習；系數重建

高維數據在信息技術高速發展的今天變得越來越普遍，它們通常分布在不同的子空間，這不僅增加了計算機內存的需求量和算法的執行時間，還會對算法[1]的性能產生不利影響，使得很多傳統的聚類算法不再適用.

最近幾年，子空間聚類技術已經吸引了很多學者的關注，它基于高維數據固有的維數通常要比外圍空間的維數低很多的思想，用多個子空間對高維數據進行聚類，并且發現適合每一組數據的低維子空間.這在計算機視覺、機器學習和模式識別等方面已經有很多的應用，尤其在圖像表示[2]、聚類[3]、運動分割[4]這3個應用上的性能優異.

可以將存在的子空間聚類算法分成主要的4類：代數方法[5]、迭代方法[6-7]、統計方法[8]和基于譜聚類的方法[9-10].在這些方法中，基于譜聚類的方法已經顯示出其在計算機視覺等方面的優越性能[11-12].

譜聚類算法[13]的核心是構建一個合適的相似度矩陣.通常用2種方法來構造相似度矩陣，即距離的倒數和重建系數.1)通過計算2個數據點間的距離倒數來得到相似度，例如歐氏距離.基于距離倒數的方法可以得到數據集的局部結構，但它的值僅僅取決于2個數據點之間的距離，所以對噪聲和異常值很敏感.2)基于表示系數的方法，假設每個數據點可以被其他數據點的線性組合進行表示，并且表示系數可以被認為是一種度量.這種度量對噪聲和異常值是魯棒的，因為系數的值不僅取決于2個相連的數據點，還取決于其他的所有數據點.最近的幾篇文章已經說明在子空間聚類中表示系數的性能是優于距離倒數的.例如基于低秩表示的子空間分割算法(low rank representation, LRR)[14]和基于稀疏表示的稀疏子空間聚類算法(sparse subspace clustering, SSC)[3].

雖然LRR子空間聚類算法已經取得了不錯的聚類效果，但是此算法仍有很大的改進空間.我們將文獻[15]中的并行計算思想和文獻[16]中的增量式學習框架相結合，這樣不僅能充分利用當前的多核計算機資源，還能直接處理新增的樣本，不需要重新聚類，達到充分利用資源節省運算時間的目的.最主要地，相似度矩陣中的元素衡量的是對應樣本的相似程度，是譜聚類算法的核心，構造一個合適的相似度矩陣可以有效地提高算法的準確率.LRR子空間聚類算法直接用低秩表示所得的系數矩陣來構造相似度矩陣，這樣會包含過多的冗余關系.本文通過保留系數矩陣每列的前k個絕對值最大系數、其他位置置0，得到一個新的系數矩陣，再用此系數矩陣構造一個稀疏的樣本關系更突出的相似度矩陣.在AR數據集和Extended Yale B人臉庫上的實驗結果表明本文所提DLRRS(distributed low rank representation-based sparse subspace clustering algorithm)和SDLRRS(scalable distributed low rank representation based sparse subspace clustering algorithm)這2種算法不僅有效減少運算時間，還提高了聚類的準確率.SDLRRS算法還具備增量式學習功能.

1基于低秩表示的子空間分割算法

研究數據空間的結構在很多領域都是一個非常具有挑戰性的任務，這通常涉及到秩最小化問題.LRR算法通過求解式(1)來得到秩最小化問題的近似解:

(1)

算法1. LRR算法[14].

① 解決核范數最小化式(1)得到C=[c1,c2,…,cn]；

② 得到相似度矩陣W=|C|+|C|T；

③ 對相似度矩陣W使用譜聚類；

④ 輸出數據集矩陣Y的類分配.

2基于分布式低秩表示的子空間聚類算法

2.1基于分布式低秩表示的稀疏子空間聚類

低秩子空間分割算法可以很精確地處理小規模的數據集，但不能有效處理大規模數據集.為此，文獻[15]中提出了一種分布式低秩子空間分割算法，該算法將大規模數據集矩陣Y按列分割成t個小規模的數據矩陣{Z1,Z2,…,Zt}，然后再對這t個小規模數據矩陣進行并行處理.其中第i個LRR子問題的處理形式為

(2)

運用此分而治之的思想，不僅保證了算法所得結果的準確率，還充分利用計算機的多核硬件資源，極大地降低算法的運算時間.在分別得到t個子系數矩陣后，本文不采用文獻[15]中的投影方式來得到最后的系數矩陣，而是直接按列排成最后的系數矩陣.

另外，基于低秩表示的子空間分割和分布式低秩子空間分割這2個算法中，都是在得到系數矩陣C后，直接用此系數矩陣來構造相似度矩陣，這樣會產生大量冗余的關系，降低算法所得結果的準確率.為此，本文在得到系數矩陣后，先對系數矩陣中的每個元素取絕對值；然后保留每列的前k個最大值，其他位置的元素置為0；再次用新得到的系數矩陣來構造相似度矩陣；最后用譜聚類來得到聚類結果.具體實現過程如算法2所示.

算法2. DLRRS算法.

① 將數據集矩陣Y按列分割成t個子數據矩陣{Z1,Z2,…,Zt}；

② 進行并行計算

?

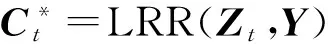
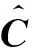
⑥ 對相似度矩陣W使用譜聚類；

⑦ 輸出數據集矩陣Y的類分配.

2.2分布式低秩增量式稀疏子空間聚類

在我們已經完成聚類得到聚類結果后，如果此時有新的樣本加入，傳統的聚類算法只有重新聚類所有樣本，不具備增量學習的功能，會導致計算資源的浪費.在文獻[16]中，提出了一種先聚類后分類的增量式聚類算法.本文參考此結構，先進行聚類，然后再用協同表示分類算法對新增的樣本進行分類.協同表示分類需要求解的目標函數為

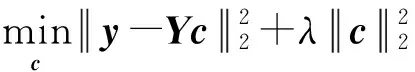
(3)

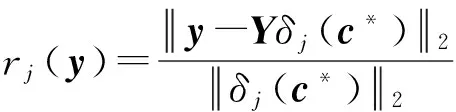
(4)

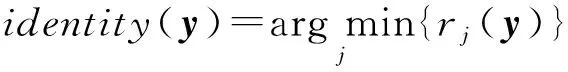
(5)

其中，δj(c*)表示保留系數列向量c*中對應第j類的元素，其他元素置為0；rj(y)表示樣本y屬于第j類的標準化殘差.

最后通過式(5)得到最終的分類結果.基于分布式低秩表示的可拓展稀疏子空間聚類算法的實現過程如算法3所示.

算法3. SDLRRS算法.

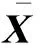
② 在數據矩陣X上運行DLRRS算法，得到聚類結果；

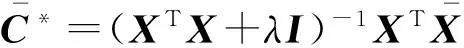
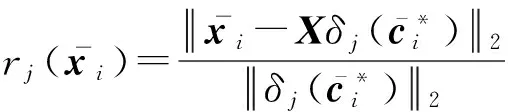
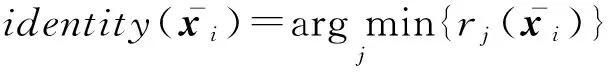
⑥ 輸出數據矩陣Y的類分配.

3實驗結果與分析

(6)

本節我們使用子空間聚類準確率(式(6))和歸一化互信息(normalized mutual information, NMI)來評估本文基于分布式低秩表示的子空間聚類算法的性能.同時，為了驗證本文算法的有效性，實驗通過3方面來進行比較分析：1)通過實驗將本文算法的參數調到最佳；2)討論并行計算分割數t對DLRRS算法的影響；3)討論SDLRRS算法增量學習功能的有效性.

其中用到的參考算法有分布式低秩子空間分割算法(distributed low-rank subspace segmentation, DFC-LRR)[15]、基于低秩表示的子空間分割算法(low rank representation, LRR)[14]、稀疏子空間聚類算法(sparse subspace clustering, SSC)[3]、可拓展的基于低秩表示的子空間分割算法(scalable low rank representation, SLRR)[16]和可拓展的稀疏子空間聚類算法(scalable sparse subspace clustering, SSSC)[16].后2種算法分別用LRR和SSC算法先進行聚類，當有新樣本加入時再用分類的方法得到結果.實驗在同一臺PC機(CPU：3.20 GHz，內存：8 GB)上進行，操作系統版本為64位Windows 8，實驗工具為MATLAB R2013a.

實驗選用2個常用的人臉數據集：AR數據集和Extended Yale B數據集.其中AR數據集包含超過4 000幅126個人(70個男性、56個女性)的人臉圖片，這些圖片是在不同的表情、不同光照和偽裝(戴墨鏡或圍巾)下得到的.每個人有26幅圖片，其中14幅“干凈”圖片、6幅戴墨鏡、6幅戴圍巾.這里我們參照文獻[17]，從50個男性和50個女性的圖片中隨機選出1 400幅“干凈”的人臉圖片.Extended Yale B人臉庫中有38個人，每個人在不同光照條件下得到64張正面人臉圖像,每個人臉圖像經過裁

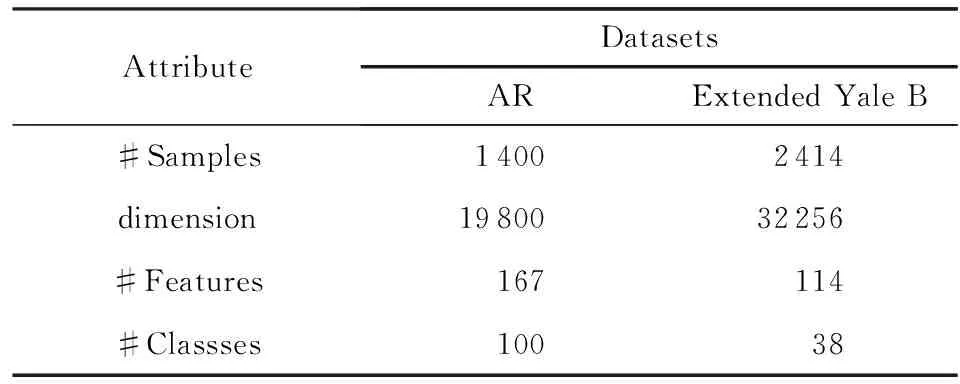
Table 1　Datasets Used in Our Experiments

剪后有192×168個像素.為了降低所有算法的計算復雜度和對內存的需求量，我們將AR數據集中的圖片下采樣到55×40，Extended Yale B人臉庫中的圖片都下采樣到48×42個像素，并且對它們進行PCA保留98%的信息.各個數據集的詳細信息如表1所示.

3.1參數對本文算法的影響

本文所提的2種子空間聚類算法包含3個參數：平衡參數λ、每列保留的系數個數k和并行計算的分割數t.本節只討論平衡參數λ和每列保留的系數個數k對DLRRS和SDLRRS這2種算法聚類質量的影響，先設置t=1，3.2節再詳細討論參數t對算法的影響.

圖1(a)(b)展示了在AR數據集上參數λ和k對DLRRS算法的影響.當λ逐漸增大的時候，對應的聚類準確率和NMI也逐漸升高，然后趨于穩定.當k從3變到8時，對應的聚類準確率從65.36%變到85.93%，NMI從81.78%變到93.66%;當k繼續增大時，對應的聚類準確率和NMI呈現出緩慢下降的趨勢.所以DLRRS算法在AR數據集上的參數選擇為平衡參數λ=2.2和保留的系數個數k=8.

圖1(c)(d)展示了在Extended Yale B數據集上參數λ和k對本文算法的影響.當λ從0.05變到2時，對應的聚類準確率從29.41%變到86.45%，NMI從38.37%變到91.15%;當λ從2變到3.8時，對應的聚類準確率和NMI基本保持不變.當k從3變到9時，對應的聚類準確率從71.58%變到86.62%，NMI從81.70%變到91.84%;在k=9時DLRRS算法取得最好的聚類質量;當k從9變到20時，對應的聚類準確率從86.62%一直下降到78.38%，NMI從91.84%下降到86.27%.所以DLRRS算法在Extended Yale B數據集上的參數選擇為平衡參數λ=2和保留的系數個數k=9.

由于篇幅所限，在此直接給出SDLRRS算法的參數設置，在AR數據集上為平衡參數λ=3.1和保留的系數個數k=6，在Extended Yale B數據集上為平衡參數λ=2.9和保留的系數個數k=5.

3.2分割數t對算法質量的影響

由于實驗室只有4核處理器，所以分割數t取1～4，然后在AR和Extended Yale B數據集上進行DLRRS和DFC-LRR這2個算法的對比實驗.

1) 橫向比較.從表2可以看出，在AR數據集上，本文DLRRS算法的聚類準確率較DFC-LRR算法高出5%左右，兩者的運算時間基本一致，DLRRS算法稍優一點;在Extended Yale B數據集上，DLRRS算法在聚類準確率方面高出DFC-LRR算法18%左右，在運算時間方面可以節省10 s左右.主要有2方面原因使得本文DLRRS算法完全優于DFC-LRR算法:①保留系數矩陣每列的前k個絕對值最大系數，其他位置置0，然后再構造稀疏的相似度矩陣是有效提高本文算法準確率的關鍵;②在并行計算時，不采用投影的方式，而是直接按列排成最后的系數矩陣，在保證聚類準確率的同時可以減少算法的運算時間.

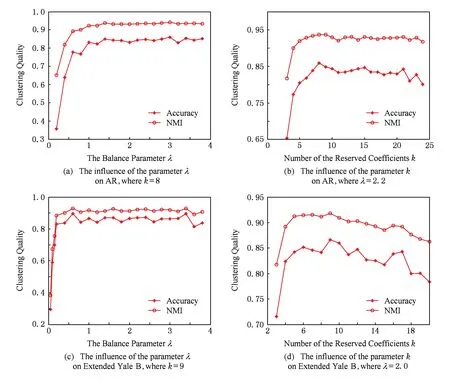
Fig. 1　Clustering quality of DLRRS with varying parameters.圖1　參數對本文DLRRS算法聚類質量的影響

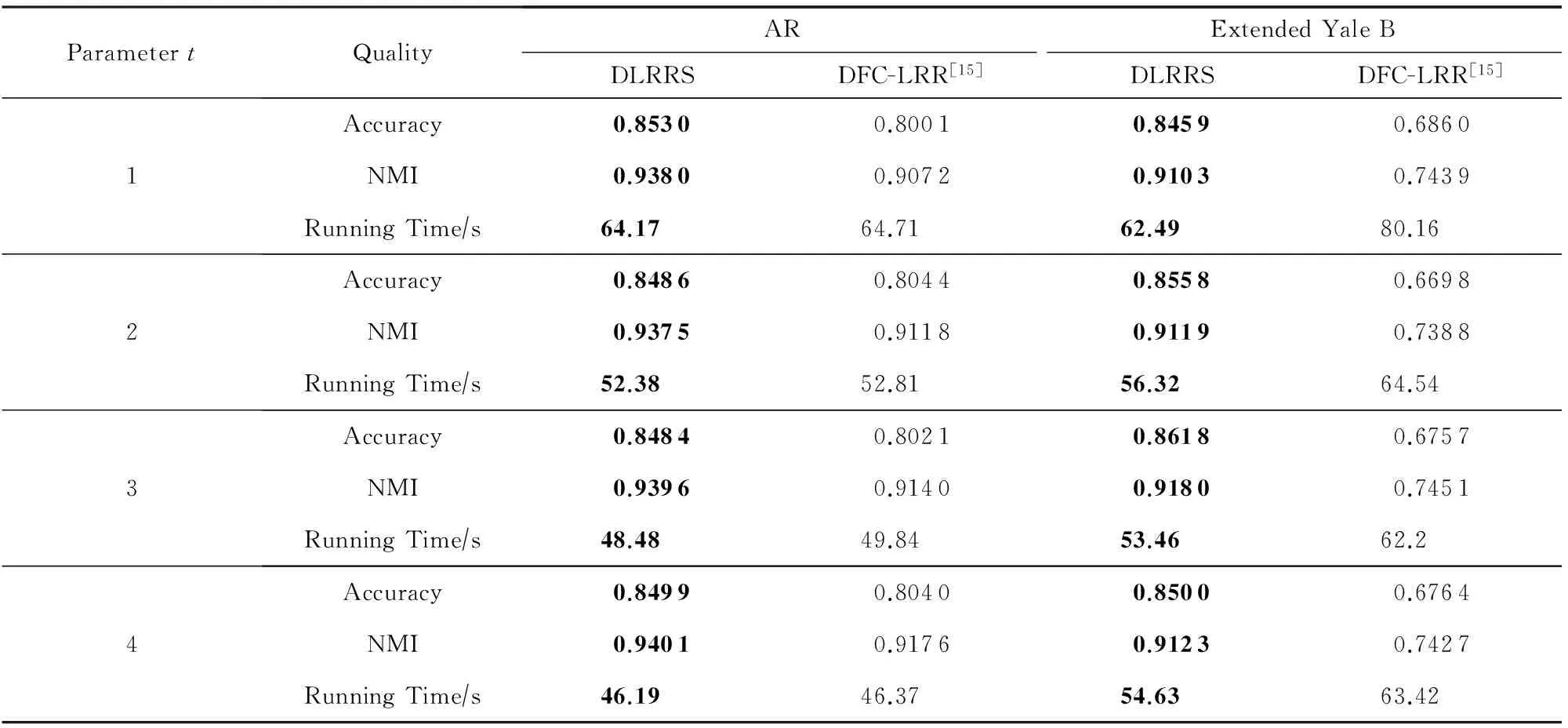
ParametertQualityARExtendedYaleBDLRRSDFC-LRR[15]DLRRSDFC-LRR[15]1Accuracy0.85300.80010.84590.6860NMI0.93800.90720.91030.7439RunningTime∕s64.1764.7162.4980.162Accuracy0.84860.80440.85580.6698NMI0.93750.91180.91190.7388RunningTime∕s52.3852.8156.3264.543Accuracy0.84840.80210.86180.6757NMI0.93960.91400.91800.7451RunningTime∕s48.4849.8453.4662.24Accuracy0.84990.80400.85000.6764NMI0.94010.91760.91230.7427RunningTime∕s46.1946.3754.6363.42

2) 縱向比較.表2所示為并行計算的分割數t對算法的影響.可以很直觀地看出，隨著t的增大，DLRRS和DFC-LRR這2個算法的聚類準確率在AR和Extended Yale B數據集上幾乎不受影響，但卻可以大幅降低算法的執行時間;t=4時較t=1時在AR數據集上可以節省28%左右的時間，在Extended Yale B數據集上可以節省13%左右的時間.由于實驗室的計算機只有4核，當t從1變到2時，DLRRS算法在2個數據集上的執行時間降幅最大，分別為18%和9.8%;當t從2變到3時，執行時間的降幅會變小;當t從3變到4時，執行時間的降幅變得不是很明顯，在Extended Yale B數據集上相較t=3時還出現了小幅度的上升，這是由于實驗室CPU只有4核，在t=4滿負荷運算時不可能只執行并行計算的代碼，還要執行其他指令，這并不影響本文算法的有效性.綜上，我們可以預見如果計算機的核數變得更多、數據集的規模變大，本文DLRRS算法在犧牲有限準確率的同時，節省運算時間的優勢會更加明顯.

3.3增量學習功能

對已經聚類好的樣本，如果此時有新樣本加入，DLRRS算法需要重新聚類.為此，本文在DLRRS算法的基礎上提出SDLRRS算法使其具備增量學習功能.為了驗證SDLRRS算法的性能，我們分別將AR和Extended Yale B數據集中的一半樣本隨機選出作為新加入的樣本進行測試，并和同樣具備增量學習功能的SLRR算法和SSSC算法進行對比.對于DLRRS，LRR和SSC這3種不具備增量學習功能的聚類算法直接使用全部樣本進行聚類測試.表3給出了不同算法在AR和Extended Yale B數據集上的聚類結果，同時列出了各個算法使用的參數，其中λ是平衡參數，k指系數矩陣中每列保留的系數個數，t是并行計算的分割數，μ是進行交替方向乘子法計算時的懲罰參數. 3.2節我們已經知道并行計算分割數t對DLRRS算法的聚類準確率影響很小，為了方便討論SDLRRS算法增量學習的效果，本節我們設置t=1.

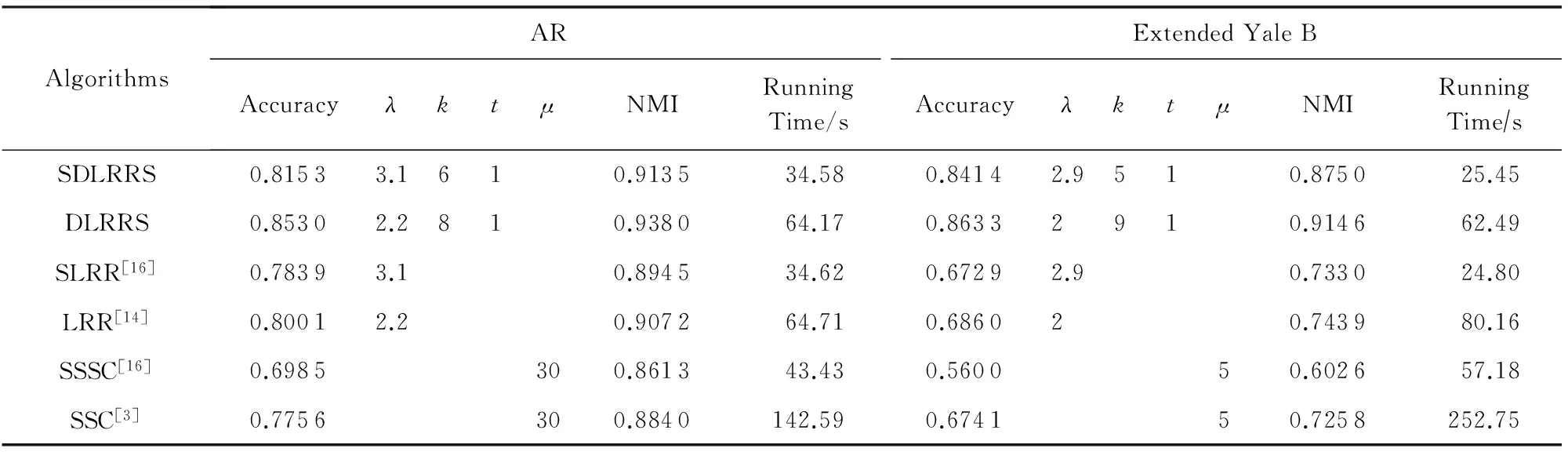
Table 3　Clustering Quality Comparison of Different Algorithms on Datasets

從表3可以看出，SDLRRS算法和DLRRS算法的聚類準確率分別較SLRR算法，LRR算法在AR數據集上有4%左右的提升，在Extended Yale B數據集上有17%的提升.當有新的樣本加入時，DLRRS，LRR，SSC這3種算法不得不對所有樣本重新聚類，導致大量資源浪費.而可拓展的3種聚類算法SDLRRS，SLRR，SSSC可以直接處理新加入的樣本，不需要對所有樣本重新聚類.在AR數據集上的準確率，SDLRRS算法比DLRRS算法低3.80%，SLRR算法比LRR算法低1.62%，SSSC算法比SSC算法低7.71%；在Extended Yale B數據集上的準確率，SDLRRS算法比DLRRS算法低2.19%，SLRR算法比LRR算法低1.31%，SSSC算法比SSC算法低11.41%，可以驗證可拓展算法的有效性.尤其是本文的可拓展聚類算法SDLRRS，比進行了重新聚類的LRR算法在AR數據集上的準確率還高出1.52%，在Extended Yale B數據集上高出15.54%；比SSC算法在AR數據集上高出3.97%，在Extended Yale B數據集上高出17.73%.另外，SDLRRS算法的運算時間相較LRR算法和SSC算法至少節省一半以上，所以SDLRRS算法不僅可以用來處理新增加的樣本，必要的時候還可以用來快速聚類整個數據集，足見本文算法是非常有效可行的.

4結束語

本文首先設計了一種基于分布式低秩表示的稀疏子空間聚類算法，此算法運用并行計算思想，并且通過保留系數矩陣每列的前k個絕對值最大系數、其他系數置為0，達到簡化突出樣本間相似程度的目的，此算法具有充分利用計算資源節省運算時間和提高聚類準確率的優點.但它不具備增量學習功能，為此，又提出一種基于分布式低秩表示的增量式稀疏子空間聚類算法，在AR數據集和Extended Yale B人臉庫上的聚類效果優異.但是，本文的研究工作還有待進一步深入和擴展，如新增加的樣本不屬于前面聚類的類，這時就不可以簡單地根據前面的聚類結果對新增樣本進行分類.

參考文獻

[1]Ying Wenhao, Xu Min, Wang Shitong, et al. Fast adaptive clustering by synchronization on large scale datasets[J]. Journal of Computer Research and Development, 2014, 51(4): 707-720 (in Chinese)(應文豪, 許敏, 王士同, 等. 在大規模數據集上進行快速自適應同步聚類[J]. 計算機研究與發展, 2014, 51(4): 707-720)

[2]Hong W, Wright J, Huang K, et al. Multiscale hybrid linear models for lossy image representation[J]. IEEE Trans on Image Processing, 2006, 15(12): 3655-3671

[3]Elhamifar E, Vidal R. Sparse subspace clustering: Algorithm, theory, and applications[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2013, 35(11): 2765-2781

[4]Zhuang L, Gao H, Lin Z, et al. Non-negative low rank and sparse graph for semi-supervised learning[C]Proc of IEEE CVPR’12. Piscataway, NJ: IEEE, 2012: 2328-2335

[5]Vidal R, Ma Y, Sastry S. Generalized principal component analysis (GPCA)[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2005, 27(12): 1945-1959

[6]Zhang T, Szlam A, Lerman G. Median k-flats for hybrid linear modeling with many outliers[C]Proc of the 12th Int Conf on Computer Vision Workshops. Piscataway, NJ: IEEE, 2009: 234-241

[7]Lu L, Vidal R. Combined central and subspace clustering for computer vision applications[C]Proc of the 23rd Int Conf on Machine learning. New York: ACM, 2006: 593-600

[8]Rao S, Tron R, Vidal R, et al. Motion segmentation in the presence of outlying, incomplete, or corrupted trajectories[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2010, 32(10): 1832-1845

[9]Favaro P, Vidal R, Ravichandran A. A closed form solution to robust subspace estimation and clustering[C]Proc of IEEE CVPR’11. Piscataway, NJ: IEEE, 2011: 1801-1807

[10]Elhamifar E, Vidal R. Clustering disjoint subspaces via sparse representation[C]Proc of IEEE ICASSP’10. Piscataway, NJ: IEEE, 2010: 1926-1929

[11]Vidal R. A tutorial on subspace clustering[J]. IEEE Signal Processing Magazine, 2010, 28(2): 52-68

[12]Li Qingyong, Liang Zhengping, Huang Yaping, et al. Sparseness representation model for defect detection and its application[J]. Journal of Computer Research and Development, 2014, 51(9): 1929-1935 (in Chinese)(李清勇, 梁正平, 黃雅平, 等. 缺陷檢測的稀疏表示模型及應用[J]. 計算機研究與發展, 2014, 51(9): 1929-1935)

[13]Von Luxburg U. A tutorial on spectral clustering[J]. Statistics and Computing, 2007, 17(4): 395-416

[14]Liu G, Lin Z, Yan S, et al. Robust recovery of subspace structures by low-rank representation[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2013, 35(1): 171-184

[15]Talwalkar A, Mackey L, Mu Y, et al. Distributed low-rank subspace segmentation[C]Proc of IEEE ICCV’13. Piscataway, NJ: IEEE, 2013: 3543-3550

[16]Peng X, Zhang L, Yi Z. Scalable sparse subspace clustering[C]Proc of IEEE CVPR’13. Piscataway, NJ: IEEE, 2013: 430-437

[17]Wright J, Yang A Y, Ganesh A, et al. Robust face recognition via sparse representation[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227

Xu Kai, born in 1989. Master. His main research interests include pattern recogni-tion and data mining.

Wu Xiaojun, born in 1967. Professor and PhD supervisor. Senior member of China Computer Federation. His main research interests include pattern recognition, computer vision, fuzzy systems, neural networks, and intelligent systems.

Yin Hefeng, born in 1989. PhD candidate. Student member of China Computer Federation. His main research interests include feature extraction, sparse repres-entation and low rank representation.

收稿日期：2014-12-09；修回日期：2015-06-09

基金項目：國家自然科學基金項目(61373055)；江蘇省自然科學基金項目(BK20140419)；江蘇省高校自然科學研究計劃重大項目(14KJB520001)

通信作者：吳小俊(wu_xiaojun@jiangnan.edu.cn)

中圖法分類號TP18; TP391.4

Distributed Low Rank Representation-Based Subspace Clustering Algorithm

Xu Kai, Wu Xiaojun, and Yin Hefeng

(SchoolofInternetofThingsEngineering,JiangnanUniversity,Wuxi,Jiangsu214122)

AbstractVision problem ranging from image clustering to motion segmentation can naturally be framed as subspace segmentation problem, in which one aims to recover multiple low dimensional subspaces from noisy and corrupted input data. Low rank representation-based subspace segmentation algorithm (LRR) formulates the problem as a convex optimization and achieves impressive results. However, it needs to take a long time to solve the convex problem, and the clustering accuracy is not high enough. Therefore, this paper proposes a distributed low rank representation-based sparse subspace clustering algorithm (DLRRS). DLRRS adopts the distributed parallel computing to get the coefficient matrix, then take the absolute value of each element of the coefficient matrix, and retain the k largest coefficients per column and set the other elements to 0 to get a new coefficient matrix. Finally, DLRRS performs spectral clustering over the new coefficient matrix. But it doesn’t have incremental learning function, so there is a scalable distributed low rank representation-based sparse subspace clustering algorithm (SDLRRS) here. If new samples are brought in, SDLRRS can use the former clustering result to classify the new samples to get the final result. Experimental results on AR and Extended Yale B datasets show that the improved algorithms can not only obviously reduce the running time, but also achieve higher accuracy, which verifies that the proposed algorithms are efficient and feasible.

Key wordslow rank representation; subspace clustering; parallel computing; incremental learning; coefficients reconstruction

This work was supported by the National Natural Science Foundation of China (61373055), the Natural Science Foundation of Jiangsu Province of China (BK20140419), and the Major Program of Research Plan of the Natural Science in Higher Education of Jiangsu Province of China (14KJB520001).