基于模糊并行約簡的模糊概念漂移探測

張　任

(浙江師范大學 數理與信息工程學院,浙江 金華 321004)

?

基于模糊并行約簡的模糊概念漂移探測

張任

(浙江師范大學 數理與信息工程學院,浙江 金華 321004)

摘要：數據流挖掘是當前數據挖掘研究的一個熱點，并且數據流的類型也不盡相同。利用模糊粗糙集和F-粗糙集的基本原理和基本方法，提出了一種對模糊型數據流進行模糊并行約簡、刪除冗余屬性的方法，并運用模糊并行約簡中屬性重要性的變化探測模糊概念漂移現象。有別于傳統方法，該方法利用模糊數據的內部本質特性對模糊概念漂移進行探測，并且通過實例驗證其探測模糊概念漂移的可行性和有效性。

關鍵詞：模糊數據流；概念漂移；模糊粗糙集；F-模糊粗糙集；模糊并行約簡

引用格式：張任. 基于模糊并行約簡的模糊概念漂移探測[J].微型機與應用，2016,35(12)：55-58.

0引言

信息爆炸的今天,現實中的數據往往隨著時間的變化而變化，例如，電商銷售數據、微博數據、傳感器數據等，這種類型的數據稱為數據流[1]。數據流具有按照時間順序排列、快速變化、連續、海量甚至無限且可能出現概念漂移現象等特征[2-3]。探測概念漂移常用的技術是滑動窗口技術[1]。參考文獻[4-6]對單個的數據塊或單棵決策樹進行冗余屬性刪除，沒有從整體上考慮刪除冗余屬性問題，再檢測概念漂移。參考文獻[7]從整體上考慮刪除冗余屬性問題，但是未能解決數據流中模糊屬性約簡問題。

粗糙集理論[8]是一種處理不相容、不精確或不完全數據的強有力工具。模糊粗糙集是粗糙集理論的擴展研究，它解決了粗糙集約簡處理之前必需的離散化過程，使得粗糙集也適用于模糊概念和模糊知識的屬性約簡。基于模糊粗糙集的屬性約簡取得了一定的研究成果[9-12]。傳統的模糊粗糙集理論不太適合研究海量的、動態變化的數據，也不太適合研究數據流；F-粗糙集[13-14]將粗糙理論從單個信息表或決策表推廣到多個，適合研究海量的、動態變化的數據，也適合研究數據流,F-模糊粗糙集[15]是該理論的擴展研究。模糊并行約簡是與F-模糊粗糙集合相對應的屬性約簡理論和方法。模糊并行約簡和F-模糊粗糙集比較適合研究海量的、動態變化的數據，也應該能夠研究模糊數據流和模糊概念漂移。

本文首先利用F-模糊粗糙集的模糊并行約簡理論，將模糊數據流的各個滑動窗口(子決策表)中對分類不起作用的冗余模糊屬性整體刪除，然后運用各個子表(滑動窗口)中屬性重要性的變化探測模糊概念漂移。傳統方法主要依靠分類準確率的變化利用外部特性進行比較，探測概念漂移現象。本文方法與傳統的概念漂移探測方法不同，利用數據的內部特性——模糊并行約簡后屬性重要性的變化探測模糊概念漂移現象。

1基礎知識

本節介紹F-模糊粗糙集和模糊并行約簡[15]的基礎知識。本文若未特別說明,屬性均表示模糊條件屬性。

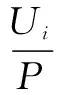
定義1在信息系統簇FIS中,模糊概念X在關系P下的模糊粗糙上下近似(簡寫為上下近似)分別為：

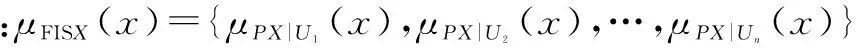
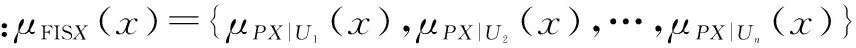
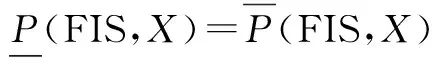
定義2在ISi中條件屬性的模糊等價類E的模糊正域為：

x對模糊正域的隸屬度為：

其中,j={1,2,…,cj}，cj是由d劃分論域U所得模糊等價類的數目,E∈GD(P|Ui)。

定義3設DS=(U,A,d)是一個決策系統，P(DS)是DS的冪集，F?P(DS)，則P?A稱為F-模糊并行約簡，當且僅當P?A滿足下面條件：

(1)μPOS(F,A,d)=μPOS(F,P,d)；

(2)對任意S?P，都有μPOS(F,S,d)≠μPOS(F,A,d)。

2模糊并行約簡方法對概念漂移的探測

在F-模糊粗糙集[15]中決策子系統簇F中的元素可以是大數據中的一部分，也可以是模糊數據流中的一部分或是一個滑動窗口。本文假設模糊決策子系統簇F中的元素是數據流中的一部分，每一個子表可以看做一個滑動窗口。在探測模糊概念漂移之前，先用模糊并行約簡算法刪除對分類不起作用的冗余模糊屬性，以減少計算量，并探測真正使模糊概念發生漂移的屬性之變化。

2.1模糊并行約簡算法

在F-模糊粗糙集中依賴度與屬性重要性的定義如下[15]。

定義4在FIS={ISi}(i=1,2,…,n)中決策屬性對條件屬性集P的依賴度為：

定義5給定一個決策子系統簇F,DTi=(Ui,A,d)∈F(i=1,2,…,n),定義F中屬性a∈P或a∈A-P相對于P的重要度分別為:

σ(P,a)=γ(F,P,d)-γ(F,P-{a},d)或σ′(P,a)=γ(F,P∪a,d)-γ(F,P,d)

運用屬性重要度可以比較容易地求出并行約簡，算法如下。

算法1 基于F-模糊屬性重要度的模糊并行約簡算法(簡稱F-PRAS)輸入:F?P(DS);輸出:F的一個模糊并行約簡;(1)P=?;(2)對于任意a∈A,如果σ(A,a)>0,那么P=P∪{a};(3)M=A-a;(4)重復進行如下步驟,直到M=?:①對任意a∈M,計算σ'(P,a)//σ'(P,a)=γ(F,P∪a,d)-γ(F,P,d);②對任意a∈M,如果σ'(P,a)≤ξ//1>ξ≥0為給定的閾值,那么M=M-{a};③選擇F-屬性重要度非零且最大的元素a∈E,P=P∪{a},M=M-{a}(添加屬性集M中F-屬性重要度非零且最大的屬性到并行約簡P中);(5)輸出并行約簡P。

2.2模糊概念漂移探測

通過模糊并行約簡刪除了數據流中對分類不起作用的冗余模糊屬性。受參考文獻[7，13-14]中屬性重要性矩陣的啟發，建立數據流約簡后的屬性重要性矩陣，用于描述在不同的模糊決策子表(滑動窗口)中模糊并行約簡中的每個模糊屬性對分類的貢獻，它的定義如下。

定義6DS=(U,A,d)是一個模糊數據流決策系統，P(DS)是DS的冪集，F?P(DS)是數據流DS=(U,A,d)的若干個滑動窗口的集合，P?A是F的模糊并行約簡，模糊并行約簡P?A關于F的屬性重要度矩陣定義為：

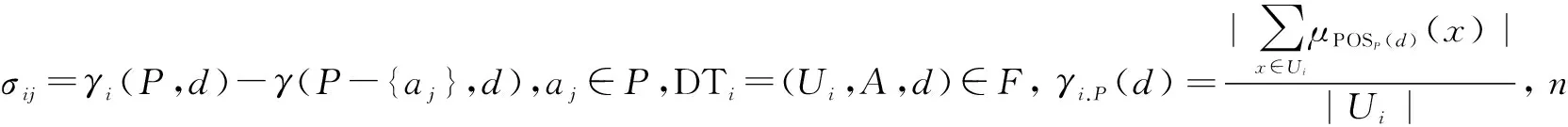
根據屬性重要性矩陣的定義，很容易證明屬性重要性矩陣的下列屬性。

定理1模糊數據流決策子表簇F?P(DS)中，P?A為并行約簡，模糊屬性重要性矩陣T(P,F)中的元素與模糊屬性重要性矩陣T(A,F)中相應的元素有如下關系：

(1)若屬性p∈P?A為模糊并行約簡的核屬性，則p在T(P,F)中對應的元素值小于等于p在T(A,F)中對應的元素值。

(2)若屬性p∈P?A為模糊并行約簡的非核屬性，則p在T(P,F)中對應的元素值大于等于p在T(A,F)中對應的元素值。

推論模糊數據流決策子表簇F?P(DS)中，P?A為模糊并行約簡，屬性重要性矩陣T(P,F)中非零元素的個數大于等于T(A,F)中非零元素的個數。

運用粗糙集理論對概念漂移進行度量的指標[16-17]往往依賴于上下近似，這種度量不太適合大小不一致的滑動窗口。參考文獻[7]的并行約簡探測算法不適合探測模糊型數據流的模糊概念漂移問題。下面運用屬性重要性的變化對模糊概念漂移進行度量，它獨立于上下近似的變化，也獨立于滑動窗口的大小。它的定義如下。

定義7模糊數據流決策子表簇F?P(DS)中，P?A為模糊并行約簡，兩個滑動窗口DTi、DTk∈F相對于屬性b∈P?A的概念漂移定義為：

FPRCDb(DTk,DTi)=|σkj-σij|

其中，j為屬性b∈P?A在T(P,F)中所對應的列。

定義8模糊數據流決策子表簇F?P(DS)中，P?A為模糊并行約簡，DTi、DTk∈F,基于模糊并行約簡P?A的模糊概念漂移量定義為：

定理2基于模糊并行約簡的屬性重要性的模糊概念漂移量FPRCDb(DTk,DTi)和FPRCDp(DTk,DTi)對稱、非負、滿足三角不等式。

定理3模糊數據流決策子表簇F?P(DS)中，DTi，DTk∈F,P?A為模糊并行約簡，則T(P,F)中相鄰兩行對應屬性重要性變化的元素個數大于等于T(A,F)中相鄰兩行對應屬性重要性變化的元素個數。

定理1、定理3說明冗余屬性的存在干擾了概念漂移的探測，刪除了一些冗余屬性后模糊概念漂移更明顯。下面利用基于模糊并行約簡的模糊概念漂移量來探測概念漂移。

通過算法2可知,模糊并行約簡將模糊決策子表簇作為一個整體考慮，刪除了模糊決策子表簇中對分類不起作用的冗余屬性，使得在模糊概念漂移的探測和分類的時候減少了計算量，并將注意力真正集中到對分類起關鍵作用的屬性集合上。基于模糊并行約簡探測概念漂移時，提供了同樣的模糊屬性和同樣的標準，得到結論的可理解性與可靠性就會更加可信。

例1模糊決策系統DS=(U,A,d)(如表1所示),U={1,2…,10}為論域,P1、P2、P3為模糊條件屬性,d為模糊決策屬性。F={DSi}(i=1,2)是DS的模糊決策子系統 ,FIS={ISi}(i=1,2)是與F相對應的模糊決策系統簇，如表2、表3所示。

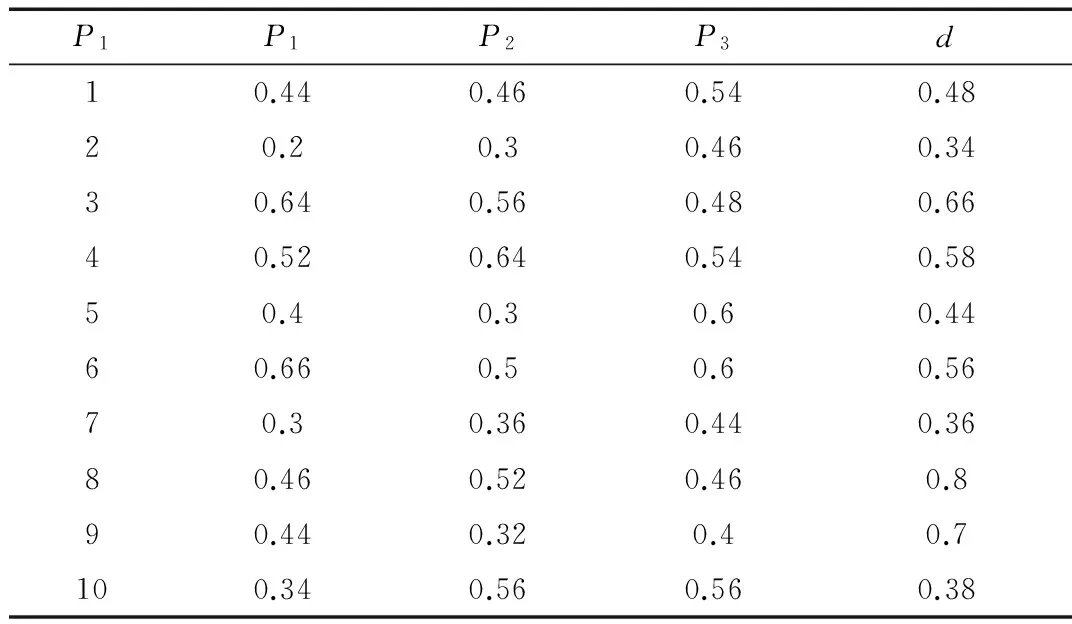
表1　模糊決策表DS

調用算法1，很容易得到F的模糊并行約簡為P={P2,P3}，子表中對象對模糊正域的隸屬度如表4所示。

表4　在子表IS1、IS2中對象對模糊正域的隸屬度

模糊屬性重要性矩陣T(A,F)與T(P,F)分別為：

DT1與DT2之間的概念漂移為：

FPRCDp2(DT2,DT1)=|0.20-0.20|=0

FPRCDp3(DT2,DT1)=|0.06-0.10|=0.04

因為條件屬性P1對分類不起作用，是冗余的屬性，刪除之后，對分類起作用的屬性P2、P3的概念漂移就彰顯出來了。如果取δ=0.01，那么相對于單個屬性P2、P3具有概念漂移，相對于整個并行約簡P也具有概念漂移；如果取δ=0.05，那么相對于單個屬性P2、P3及相對于并行約簡P都不具有概念漂移。實際的數據流中，滑動窗口一般情況下是多個，可以類似地求出兩個相鄰窗口之間的基于模糊并行約簡的概念漂移量。

3結論

傳統的概念漂移探測方法不能探測模糊數據流中模糊概念漂移,并且其主要利用分類準確率的變化對概念漂移現象進行探測。本文提出了一種基于模糊并行約簡的概念漂移探測方法。本文方法利用模糊數據的內部特性——模糊并行約簡后的屬性重要性的變化探測模糊概念漂移現象。

下一步的工作是研究模糊并行約簡探測模糊概念漂移中δ的最佳取值，以及具體運用模糊并行約簡構建分類器，與傳統的概念漂移方法進行深入的分析比較。

參考文獻

[1] BABCOCK B, BABU S, DATER M,et al. Models and issues in data stream systems[C]. Proceedings of the 21st ACM SIGACT-SIGMOD-SIGART Sympsium on Principles Database Systems, Madison, USA, 2002:1-6.

[2] 王濤, 李舟軍, 顏躍進, 等. 數據流挖掘分類技術綜述[J]. 計算機研究與發展, 2007, 44(11):1809-1815.

[3] 徐文華, 覃征, 常揚. 基于半監督學習的數據流集成分類算法[J]. 模式識別與人工智能, 2012, 25(2): 292-299.

[4] Jin Ruoming, AGRAWAL G. Efficient decision tree construction on streaming data[C].Proceedings of the ACM SIGKDD the 9th International Conference on Knowledge Discovery and Data Mining, Washington, USA, 2003:571-576.

[5] 辛軼, 郭躬德, 陳黎飛,等. IKnnM-DHecoc:一種解決概念漂移問題的方法[J].計算機研究與發展, 2011, 48(4):592-601.

[6] 琚春華，帥朝謙，封毅，基于粒計算的商業數據流概念漂移特征選擇[J].南京大學學報(自然科學版)，2011，47(4):391-397.

[7] 鄧大勇, 徐小玉, 黃厚寬. 基于并行約簡的概念漂移探測[J]. 計算機研究與發展, 2015, 52(5):1071-1079

[8] PAWLAK Z. Rough sets[J]. International journal of Information and Computer Science, 1982,11(5): 341-356.

[9] JENSEN R , Shen Qiang. Fuzzy-rough sets for descriptive dimensionality reduction[C].Proceedings of 11th International Conference on Fuzzy Systems, Hawaii, 2002: 29-34.

[10] 李興寬.集值信息下的粗集與知識獲取[J].微型機與應用,2015,34(23):14-15.

[11] 程昳,苗奪謙,馮琴榮.基于模糊粗糙集的粒度計算[J]. 計算機科學,2007,34(7):142-149.

[12] 徐菲菲,苗奪謙,魏萊,等.基于互信息的模糊粗糙集屬性約簡[J]. 電子與信息學報，2008,30(6):1372-1375.

[13] 王國胤, 李德毅, 姚一豫，等.云模型與粒計算[M].北京：科學出版社, 2012.

[14] 陳林. 粗糙集中不同粒度層次下的模糊并行約簡及決策[D]. 金華：浙江師范大學，2013.

[15] 鄧大勇, 徐小玉, 裴明華. F-模糊粗糙集及其并行約簡[J]. 浙江師范大學學報(自然科學版), 2015, 38(1):58-66.

[16] 鄧大勇, 裴明華, 黃厚寬. F-粗糙集方法對概念漂移的度量[J]. 浙江師范大學學報(自然科學版), 2013, 36(3):303-308.

[17] Yao Yiyu. Three-way decision with probabilistic rough sets[J].Information Sciences, 2010, 180:341-353.

中圖分類號：TP18

文獻標識碼：A

DOI：10.19358/j.issn.1674- 7720.2016.12.018

(收稿日期：2015-12-18)

作者簡介：

張任(1989-),男,碩士研究生,主要研究方向:粗糙集、模糊集、數據挖掘。

Algorithms of fuzzy concept drifting detection for categorical evolving data based on fuzzy parallel reducts

Zhang Ren

(College of Mathematics, Physics and Information Engineering, Zhejiang Normal University, Jinhua 321004, China)

Abstract:Data stream mining is one of hot topics of data mining,and the types of data flow are different. Based on basic principles of fuzzy rough sets and F-fuzzy rough sets, this paper presents a new method of fuzzy parallel reducts to reduce redundant attributes from fuzzy data stream, and detect fuzzy concept drifting according to the attribute significance of fuzzy parallel reducts. Different from other classical methods，the inner properties of data stream are used to detect concept drifting.Through examples it verifies its feasibility and validity.

Key words:fuzzy data streams; concept drift; fuzzy rough sets; F-fuzzy rough sets; fuzzy parallel reducts