基于改進TOPSIS模型的地鐵網絡節點重要性評價方法

許海霖，張　晶

(首都師范大學資源環境與旅游學院，北京　100048)

?

基于改進TOPSIS模型的地鐵網絡節點重要性評價方法

許海霖，張晶

(首都師范大學資源環境與旅游學院，北京100048)

摘要：對城市地鐵網絡節點重要性進行評價在城市交通體系的運營和管理中具有重要意義。TOPSIS法是一種節點重要程度多指標綜合評價方法。已有的TOPSIS法在評價地鐵網絡節點重要程度時存在貼近度評價不合理，權重算法沒有考慮網絡空間特性兩方面問題。針對上述不足，提出相應的改進措施：(1)結合垂面距離和灰色關聯度綜合評價方案與理想解的貼近度；(2)設計適用于空間網絡的局部熵賦權法。最后，以北京地鐵網絡為例，利用改進的TOPSIS法測算了節點的重要性程度。結果表明：該方法確定的結果符合實際情況并且優于現有的TOPSIS法，說明該方法具有較高的準確性和較強的應用性。

關鍵詞：地鐵網絡；節點重要性；綜合評價；空間局部熵權

地鐵網絡是城市交通網絡的重要組成部分。由于網絡結構的異質性，使得網絡中的每個節點的重要程度是不同的[1]，有效識別地鐵網絡中的重要節點對于合理分配有限的網絡節點資源，提高網絡效率和可靠性，預防客流波動、設備故障等隨機因素可能造成的節點失效[2]具有重要意義。國內外學者對城市交通網絡節點重要度進行了大量的研究，Paolo[3]等人利用5個中心性指標對全球18個城市道路的節點中心性進行了分析，結果表明：道路節點中心性反映了不同城市結構特征。Rui[4]等對城市道路節點中心性與土地利用之間的關系進行了探索，發現多種中心性指標可以很好地揭示土地利用類型的發展模式。在國內，王力[5]等人以節點連接度、節點介數和交叉口高峰小時交通流量為評價指標，應用FCM模糊聚類方法給出交叉口的重要性分類方法，從而實現了交通網絡的關鍵節點選擇。羅金龍[6]設計了一種以介數中心性為基礎，結合最短路徑及節點破壞后的最大連通子圖來綜合評價地鐵網絡中節點重要性的方法，通過對3種指標進行線性組合得到了比單一指標更有參考價值的結果。上述研究，即采用復雜網絡的方法對交通網絡節點重要性的研究在為我們開辟新思路的同時，也給后續研究提出了新的挑戰。例如，以單一指標來評價節點的重要性是否合理？由于網絡節點的重要性與網絡結構、節點在網絡中的位置、節點與鄰居節點的關系等多方面都存在緊密的聯系，使用單一指標評價節點的重要性就顯得力不從心，評價結果具有片面性。盡管國內有些學者采用類似多指標的綜合評價方法[7，8]，但未能達到理想的研究結果，究其原因，這種多指標的綜合評價方法實質是對多個指標的依次使用，忽略了指標間的相關信息。逼近理想排序法(TOPSIS)是一種同時考慮多個指標及指標間的相關信息對方案優劣進行排序的綜合評價方法，已有學者將其用于網絡節點重要性評價[9，10]，由于涵蓋了影響節點重要性的諸多因素，因此可以得到比使用單一指標評價更為準確和客觀的重要性評價結果，但傳統的TOPSIS方法存在對方案與理想解貼近度評價不合理、普通熵權法未能考慮地鐵網絡的空間異質性等問題[11，12]。針對上述問題，從兩方面對傳統TOPSIS方法進行改進：(1)采用垂面距離-灰色關聯方法代替歐氏距離測定貼近度，從而有效避免歐氏距離對于貼近度評價不合理的問題；(2)利用空間局部熵確定各指標權重，從而達到更加準確的為各方案指標賦權的效果，并以北京地鐵網絡為例，使用改進的TOPSIS方法評估各節點的重要性，結果表明該方法具有較高的準確性和較強的應用性。

1研究方法

1.1傳統TOPSIS法存在的不足

(1)傳統的TOPSIS法在計算各方案與理想解的貼近度時使用的是歐式距離法，但是，歐式距離法有時并不能完全反映出各方案的優劣性，主要體現在兩個方面：①與理想解歐式距離近的方案有可能與負理想解歐式距離也近[13]；②以距離作為尺度僅僅能反映數據曲線之間的位置關系，而不能體現數據序列的態勢變化。在指標值相差較大的情況下，只要方案和理想方案之間的距離相近仍會得到方案優劣相近的結果[14]。

(2)權重是對評價指標重要程度的度量。選取適當的方法確定權重是整個評價過程的關鍵環節。熵權法是一種常用的客觀賦權法，它利用各指標的熵值所提供的信息量來決定權重大小[15]。

已有的熵權法采用的是一種全局熵的概念，即將所有評價方案看作一個整體，計算整體指標的熵值進而確定權重。但是在交通網絡中，由于地理空間的異質性和不穩定性，不同的子空間內信息的無序程度是變化的，不同的方案指標的權重也應是不同的，而全局熵忽視掉了這一特性，對結果起到了平滑的作用，減小了信息變化劇烈區域的熵值，增大了信息變化相對平穩區域的熵值。

1.2改進的topsis法1.2.1基于垂面距離-灰色關聯測定貼近度

鑒于常規TOPSIS法采用歐氏距離的缺陷，本文采用垂面距離結合灰色關聯代替歐氏距離確定各方案到理想解的相對貼近度。垂面距離是指在理想解和負理想解之間，以理想解與負理想解連線為法向量，分別過這兩點作兩平面，這兩平面間的距離。如圖1所示：A，B分別為理想解和負理想解，X，Y為任意兩點，P，Q為以AB為法向量過X，Y點的平面，X，Y在直線AB上的投影分別為C，D，則X，Y兩點的垂面距離就是平面P，Q間的距離，即C和D之間的歐氏距離。

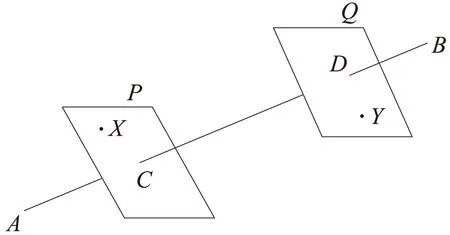
圖1　垂面距離示意

垂面距離實則是將各方案到理想解的歐氏距離轉化為方案在正負理想解連線上的投影到理想解的距離，更加準確地反映了方案與理想解的接近程度。為有效解決僅使用距離最為評判準則帶來的弊端，引入灰色關聯的思想[16]，灰色關聯是曲線形狀相似性的衡量尺度，能很好地分析態勢變化。曲線形狀越接近，相應序列之間的關聯度就越大。對于多指標決策問題來說，如果方案與理想方案灰色關聯度越大，可認為方案越接近理想方案。垂面距離和灰色關聯分別解決了傳統TOPSIS法在計算相對貼近度時兩方面的問題，因此，本文將二者有機結合，構造出一種新的更為準確的相對貼近度評價方法。

1.2.2基于空間局部熵的權重確定

由于傳統熵權法應用于交通網絡忽略了網絡的空間特性，采用局部熵的方法對其進行改進。選取某節點空間鄰域作為該節點子空間，計算子空間內的節點指標熵值為該節點賦權。這樣可以充分考慮到不同節點所在地理環境的差異，精確識別各節點所在子空間內信息的無序程度，有效避免全局熵引起的空間平滑效應。

對于網絡中某節點，設其空間鄰域有m個評價方案、n個評價指標，則評價指標熵Hj為

(1)

(2)

式中，bij為無量綱化決策矩陣中的元素。

則該節點評價指標權重為

(3)

1.2.3改進的TOPSIS法具體步驟

基于改進的TOPSIS法對地鐵網絡節點重要性評價分為以下幾個步驟。

(1)形成決策矩陣。設地鐵網絡中有m個節點，每個節點有n個評價指標，則可構成多目標決策矩陣X

(4)

(2)無量綱化決策矩陣。為了消除量綱對決策的影響，需要對各指標進行無量綱化處理，構建標準化決策矩陣V=(vij)m×n

(5)

(3)計算各方案指標權重。利用局部熵權法計算各方案指標權重。得到權重矩陣W

(6)

(4)構建加權決策矩陣。將無量綱決策矩陣中的元素與相應的權重相乘，得到加權決策矩陣Z

(7)

(5)確定矩陣Z的最優向量Z+和最劣向量Z-。

(8)

(9)

式中，Kb為效益指標，值越大，能力越強；Kc為成本指標，值越小，能力越強。

(10)

(11)

(12)

(13)

(14)

式中，ξ為分辨系數，通常取值為0.5。

(7)計算各方案的相對貼近度。將各方案到正負理想解的垂面距離和灰色關聯度進行無量綱化處理，處理公式為

(15)

將無量綱化后的垂面距離和灰色關聯度相結合

(16)

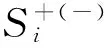
(17)

根據相對貼近度對節點重要程度進行排序，值越大，表示節點重要性越高，值越小，則節點重要性越低。

2應用實例

2.1北京市地鐵網絡

截止到2015年5月，北京市軌道交通擁有17條線路，268個站點。站點和線路分布圖如圖2所示，對軌道交通的復雜網絡建模主要有2種方法[17]，基于L空間構建軌道交通抽象網絡，建成后北京市地鐵網絡共有268個節點，303條邊，邊長最大為18 322，最小為424，實際單位為m。

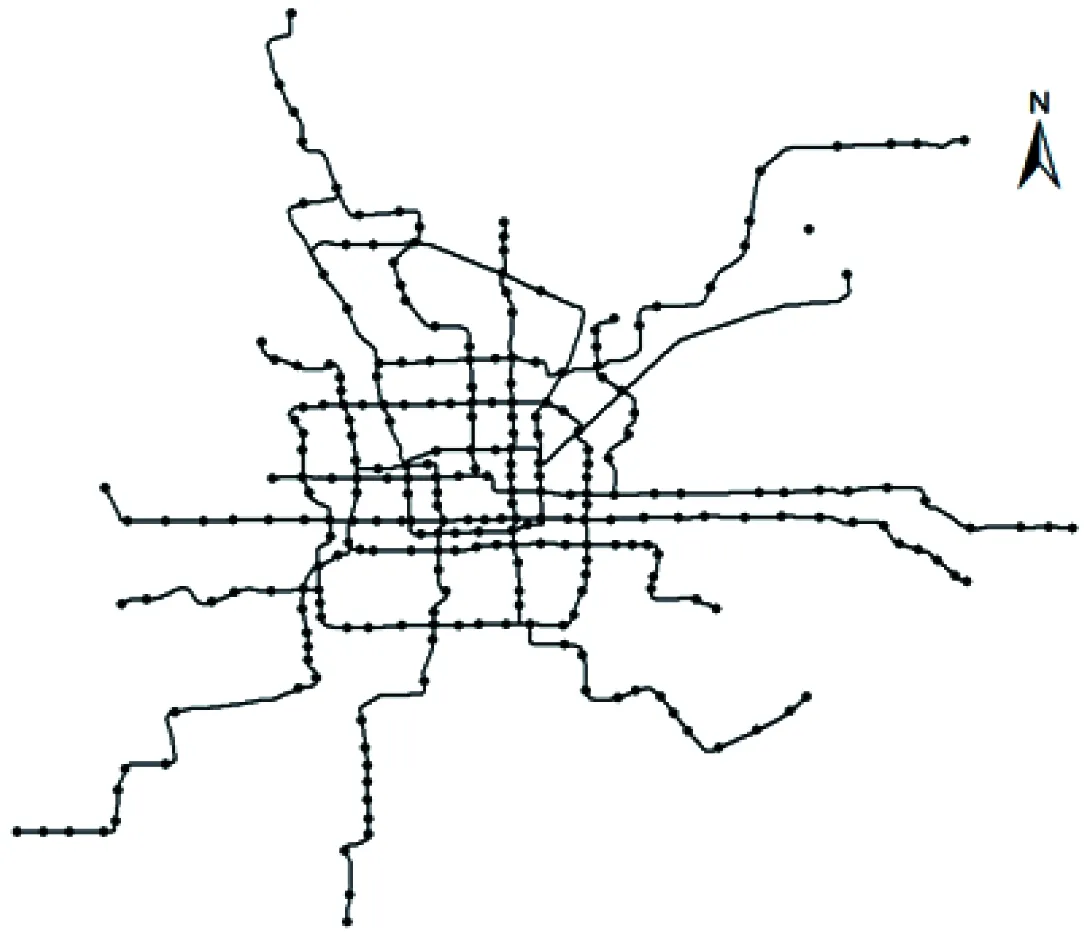
圖2　北京城市軌道交通示意

2.2地鐵網絡節點重要性評價指標

目前，對于節點重要性的單一評價指標已取得很多成果。將選取在交通網絡節點重要性單一評價指標中使用最為廣泛的度中心性(DC)，接近中心性(CC)、介數中心性(BC)[18]和特征向量中心性(EC)[19]4種中心性指標作為綜合評價指標(表 1)。

表 1　指標定義

在計算接近中心性時需要計算每個節點到網絡中其他節點的最短路徑，非空間網絡中，路徑長度指的是兩點間的拓撲距離，但在具有實際空間意義的地鐵網絡中，最短路徑應為經過兩站點最短耗時所對應的路徑，而耗時與兩站點的軌道長度直接相關，使用兩個節點間的空間距離即兩站點間的軌道長度代替拓撲距離，能夠得到更加接近實際的結果。因此，在計算CC時使用空間距離代替拓撲距離。

2.3計算網絡節點重要度

(1)建立無量綱化決策矩陣。首先計算北京地鐵網絡節點的4個中心性指標，按照式(4)～式(5)對其進行無量綱化處理，得到無量綱化決策矩陣V。

(2)計算權重。在確定節點的空間鄰域時，選擇了空間上距離某節點最近的10、20、30個節點分別進行實驗，根據網絡規模和實驗效果最終選擇20個節點作為該節點的空間鄰域，按照式(1)～式(3)計算局部熵并為該節點指標賦權。各方案指標權重匯總情況如表2所示。需要注意的是，使用兩站點間的有效軌道長度代表兩站點間的距離。

表2　權重統計匯總

(3)構建加權決策矩陣，得到理想解。將無量綱化決策矩陣與權重矩陣相乘，得到加權決策矩陣。根據式(8)～式(9)確定理想解和負理想解，本文的4個指標都屬于效益指標。

(4)計算垂面距離和灰色關聯度，并確定最終的相對貼近度。根據式(10)～式(14)求得各方案與正負理想解的垂面距離和灰色關聯度。經無量綱化處理后，綜合各方案的灰色關聯度和垂面距離，取α=β=0.5，得出各方案綜合距離，并計算相對貼近度。

2.4結果分析及驗證

將計算結果從大到小排列，得到北京市地鐵網絡節點重要性排序，列出排名前20的站點，如表3所示。

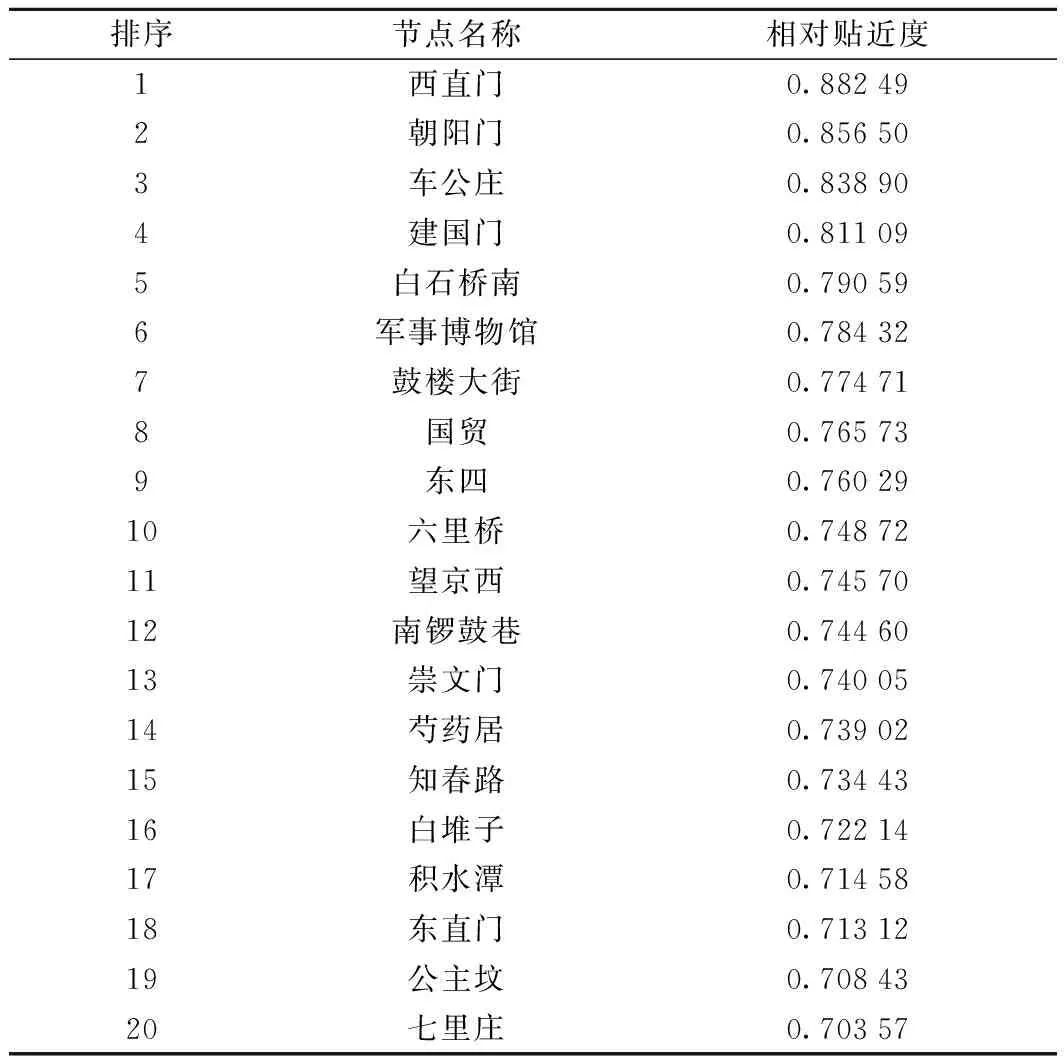
表3　北京市地鐵網絡重要節點排序

從表3可以發現，西直門是北京地鐵網絡中最重要的節點，現實中西直門是2號線、4號線和13號線的換乘站，是北京地鐵中僅有的2個3條軌道線路交匯換乘站點之一，具有網絡中最大的度值和較高的介數，是網絡中的重要交通樞紐；西直門位于北京市的西二環，靠近網絡中心，到達網絡中其他節點的最短路徑相對較短。因此，西直門在北京地鐵網絡中重要性最高。另外，這些重要性較高的節點大多為換乘站點，連接了2條或多條地鐵線路，承擔了較大的客流量，并且大多數位于北京市三環以內，接近網絡中心，具有較高的介數和較短的路徑長度。需要注意的是，望京西、七里莊這2個站點比較靠近城市邊緣，但是其依然具有很高的重要性，這是因為2個站點坐落在東北和西南地區與中心城區的連接處，雖然接近中心性低但具有很高的介數。如果這2個站點發生問題，將極大影響東北和西南地區與中心城區的聯系。從現實出發，可以看出本文方法可以有效識別出地鐵網絡中的重要站點。

網絡的最大聯通圖是指網絡中的最大聯通分量。若網絡為全聯通，則最大聯通圖為其本身。最大聯通圖相對大小S是指網絡中最大聯通圖的節點個數占原始網絡總結點個數的百分比。公式如下

(18)

式中，G′為某一時刻的網絡。

要驗證節點對網絡的重要程度可以按照認為的重要性排序依次對網絡中的節點進行攻擊，并使用S來表明攻擊后網絡的受損程度，在全聯通網絡中S的初始值為1，隨著部分節點失效，網絡會分裂成若干子圖，S也隨之下降，下降程度越快，說明受攻擊節點對網絡的影響越大，重要程度越高。按重要性程度由高到低的順序對由改進的TOPSIS方法和傳統TOPSIS方法所得節點進行攻擊，統計S的變化情況，結果如圖3所示。從圖3可以看出，改進的TOPSIS法在失效節點比例不到10%的情況下，S值已經降到0.3左右，最大連通子圖的節點個數不足原始網絡的30%，說明失效節點對于網絡的重要性。與傳統的TOPSIS方法相比，改進的TOPSIS法重要節點在受到攻擊時，S的變化更快更早，對網絡的影響更迅速更大，從而驗證了本文方法的有效性和準確性。

圖3　S變化趨勢

3結論

對地鐵網絡節點重要性進行測算具有重要的現實意義，利用TOPSIS方法對節點重要性進行綜合評價，可以彌補單一評價指標造成的評價結果片面性。本文總結了傳統TOPSIS的不足，運用垂面距離和灰色關聯度相結合的方法對其進行改進，考慮到傳統熵權法在空間網絡方面的缺陷，采用了空間局部熵方法為各方案屬性賦權。以北京地鐵網絡為例對其節點重要度進行測算，結合實際情況并通過與傳統TOPSIS方法對比說明了該方法的準確性，為進一步提高網絡可靠性和合理分配保護資源奠定了基礎。同時應該看到，在確定用來獲得指標權重的空間鄰域時，通過實驗的方法選擇最近的20個節點作為計算權重的鄰域子空間。這種通過實驗的方法所獲得的節點鄰域子空間大小是否最優，目前還沒有基于實證數據的定量的評價指標，并且不同規模和結構的網絡節點鄰域子空間也是不同的，如何通過科學方法確定不同網絡節點鄰域子空間大小，還需進一步探索。

參考文獻：

[1]赫南，李德毅，淦文燕，等.復雜網絡中重要性節點發掘綜述[J].計算機科學，2007(12):1-5，17.

[2]喬珂，趙鵬，姚向明.城市軌道交通網絡性能分析[J].交通運輸系統工程與信息，2012(4):115-121.

[3]CRUCITTI P， LATORA V， PORTA S. Centrality measures in spatial networks of urban streets[J]. Physical Review E73 (Statistical， Nonlinear， and Soft Matter Physics)， 2006，73(3):036125.

[4]Rui Yikang， Ban Yifang. Exploring the relationship between street centrality and land use in Stockholm[J]. International Journal of Geographical Information Science， 2014，28(7):1425-1438.

[5]王力，于欣宇，李穎宏，等.基于FCM聚類的復雜交通網絡節點重要性評估[J].交通運輸系統工程與信息，2010(6):169-173.

[6]羅金龍.城市軌道交通網絡復雜性及演化分析[D].北京：北京交通大學，2014.

[7]張珍，張振宇，宋蔓蔓.一種基于最短路徑介數的重要節點發現算法[J].計算機工程與應用，2013(21):98-100，132.

[8]徐敏政，許珺，陳娛.復雜網絡中連通支配中心性的計算[J].復雜系統與復雜性科學，2014(4):41-47.

[9]于會，劉尊，李勇軍.基于多屬性決策的復雜網絡節點重要性綜合評價方法[J].物理學報，2013(2):54-62.

[10]秦李，楊子龍，黃曙光.復雜網絡的節點重要性綜合評價[J].計算機科學，2015(2):60-64.

[11]華小義，譚景信.基于“垂面”距離的TOPSIS法——正交投影法[J].系統工程理論與實踐，2004(1):114-119.

[12]王福良，馮長春，甘霖.軌道交通對沿線住宅價格影響的分市場研究——以深圳市龍崗線為例[J].地理科學進展，2014(6):765-772.

[13]肖淳，邵東國，楊豐順.基于改進TOPSIS法的流域初始水權分配模型[J].武漢大學學報：工學版，2012(3):329-334.

[14]孫曉東，焦玥，胡勁松.基于灰色關聯度和理想解法的決策方法研究[J].中國管理科學，2005(4):63-68.

[15]欒婷婷，鄭云水，穆然.基于TOPSIS的鐵路應急資源供應優先級研究[J].鐵道標準設計，2015，59(12):22-26.

[16]李存斌，慶格夫，馮霞，等.基于云模型和改進TOPSIS法的電力設備狀態檢修控制策略[J]. 華東電力，2014(2):355-359.

[17]汪濤，方志耕，等.城市地鐵網絡的復雜性分析[J].軍事交通學院學報，2008，10(2) :24-27.

[18]FREEMAN L C. Centrality in social networks conceptual clarification[J]. Social Networks， 1979(1):215-239.

[19]BONACICH P. Factoring and weighing approaches to status scores and clique identification[J]. Journal of Mathematical Sociology， 1972，2(1):113-120.

收稿日期：2015-11-18； 修回日期：2015-11-30

作者簡介：許海霖(1989—)，男，碩士研究生，E-mail：173910996@qq.com。 通訊作者：張晶(1966—)，女，教授，博士生導師，E-mail：zhangjing 5946@sina.com。

文章編號：1004-2954(2016)07-0019-05

中圖分類號：U231

文獻標識碼：A

DOI:10.13238/j.issn.1004-2954.2016.07.005

Method of Identifying Influential Nodes of Subway Network Based on Improved TOPSIS

XU Hai-lin， ZHANG Jing

(Resource Environment and Tourism College， Capital Normal University， Beijing 100048， China)

Abstract：It is significant to evaluate the importance of urban subway network nodes in the operation and management of urban traffic system. TOPSIS method is one of the multi-index comprehensive methods to evaluate the importance of nodes. But the existing TOPSIS methods have insufficiencies in estimating close degree when the importance of metro network nodes is evaluated and in the weighting algorithm when the features of network space are not concluded. In view of these issues， this paper puts forward corresponding improvement measures∶1) with vertical distance and grey correlation degree to evaluate the close degree between the program and ideal solution; 2) design of local entropy weighting method suitable for the spatial network. At last， node importance of urban rail transit network of Beijing is evaluated with improved TOPSIS. The results show that the results obtained by improved TOPSIS method conform to the actual measurements and better than those with existing TOPSIS. The method is proved highly accurate and applicable．

Key words：Urban rail transit network; Nodes importance; Comprehensive evaluation; Spatial local entropy weight