采空區頂板動力響應數值模擬研究

梁 超

(昆明理工大學 國土資源工程學院，云南 昆明 650093)

?

采空區頂板動力響應數值模擬研究

梁 超

(昆明理工大學 國土資源工程學院，云南 昆明 650093)

介于巖體材料及爆破地震波的復雜性，采用理論分析方法難以對采空區頂板動力響應做出準確計算，而且求解出的計算公式通常比較復雜，工程上難以直接應用。FLAC3D數值模擬軟件中的動力分析功能在解決巖土工程方面的非線性動力分析問題方面有巨大優勢，能更深入的研究采空區頂板在爆破震動作用下的動應力場、動位移場和塑性區的變化規律及動靜應力場的疊加作用機理。在理論研究的基礎上，借助FLAC3D提供的動力分析功能，建立數值計算模型，對靜力荷載和爆破動載共同作用下采空區頂板失穩過程和機理進行數值模擬分析。

爆破地震波；動力響應；采空區頂板；數值模擬

0 前 言

爆破作業是金屬類礦山在開采過程中非常重要且必不可少的工序，不論是生產還是掘進都需要進行大量爆破作業，而爆破必然產生震動，對周圍巖體形成動力加載環境，如果動荷載強度達到某一程度會直接造成圍巖的動力失穩破壞。另一方面，采空區頂板在爆破地震波的反復動力加載作用下，其宏觀力學性能將逐漸被弱化乃至最終失效或形成連續非線性的累積損傷。所以，爆破震動效應對采空區圍巖造成的危害不能被忽略[1-3]。

介于巖體材料及爆破地震波的復雜性，采用理論分析方法難以對采空區頂板動力響應做出準確計算，而且求解出的計算公式通常比較復雜，工程上難以直接應用。而隨著計算機軟件技術的廣泛應用，為研究巖體結構動力響應提供了一種新方法。鑒于數值模擬的特點和求解非線性動力問題的優越性，用數值計算的方法來研究爆破地震作用下采空區頂板結構動力響應的規律已成為爆破領域研究方法的一個必然趨勢[57]。FLAC3D數值模擬軟件中的動力分析功能在解決巖土工程方面的非線性動力分析問題具有巨大的優勢。為更深入的研究采空區頂板在爆破震動作用下的動應力場、動位移場和塑性區的變化規律及動靜應力場的疊加作用機理，本章在前面理論研究的基礎上，借助FLAC3D提供的動力分析功能，建立數值計算模型，對靜力荷載和爆破動載共同作用下采空區頂板失穩過程和機理進行數值模擬分析。

1 數值模擬軟件概述

FLAC是連續介質快速拉格朗日差分分析方法的英文縮寫，是專門為巖土工程穩定性分析設計和服務的程序，屬于有限差分軟件。他能夠準確模擬材料的塑性破壞和流動，能夠對土質巖石材料進行力學特性模擬和塑性流動分析，具有與巖土工程實際擬合好，計算穩定性好、收斂快的特點，因此目前是包括水電、礦業、公路、鐵路等巖土工程領域求解三維問題時普遍采用的理想分析工具[4]。

FLAC3D的基本計算原理是將計算區域劃分為若干四面體單元，用節點將各個單元相互連接，當某個節點受到荷載作用后，其運動方程可以用時間步長的有限差分形式表示，并且荷載只對該節點周圍的若干節點有影響。程序根據單元節點的速度變化來計算單元之間的相對位移，進而可以求出單元應變，然后根據單元材料的本構關系即可求出單元應力。

FLAC3D中為巖土體工程問題的求解提供了11種力學模型和5種計算模式，其中巖土工程常用的力學模型有Null model開挖模型、Mohr-Coulomb塑性模型和Drucker-Prager塑性模型；而常用的計算模式有靜力模式、動力模式、滲流模式及蠕變模式。其中，靜力模式是是FLAC3D默認的計算模式。動態分析時，要先進行靜力計算，并在此基礎上打開動力計算功能，設置動態邊界然后直接施加速度或應力荷載進行動力擾動分析。

2 數值模型的建立及計算方案

2.1計算模型區域及幾何尺寸

本文根據某礦豎向排列采空區建立數值計算模型。根據礦體開挖尺寸和上部圍巖特點，設置模型尺寸的長度為290 m，寬度為220 m，高度為200 m。模型由上下兩個橫截面為矩形的采空區組成，并且不考慮上方采空區跨度的變化，兩個采空區的長寬高尺寸均為42 m×36 m×18 m。以豎直方向為模型的Z軸，沿礦體走向方向為Y軸，水平方向內垂直礦體走向設為X軸。模型的Z軸的正方向范圍即0 m≤Z≤200 m為數值計算區域，X方向的計算范圍是 ，Y方向的范圍為0 m≤Z≤290 m。網格單元的劃分采用不等劃分，根據需要對模型開挖部分的網格劃分的細一些，對模型的外部較遠的區域劃分相對稀疏。模型內共劃分了79 296個單元，85 140個節點，三維計算模型及網格劃分如圖1所示。

圖1 計算模型及網格分布

本次模擬分析中，靜力計算和動力計算均采用Mohr-Coulomb強度準則，其屈服函數為：

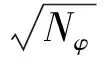
(1)

ft=σ3-σt

(2)

式中：Nφ=(1+sinφ)/(1-sinφ)，其中φ為內摩擦角；σ1，σ3分別為最大和最小主應力；c為黏聚力；σt為巖石抗拉強度。當巖體內某一點應力滿足fs<0時發生剪切破壞；當巖體內某一點應力滿足ft>0時發生剪切破壞。計算所需的巖體力學參數見表1。

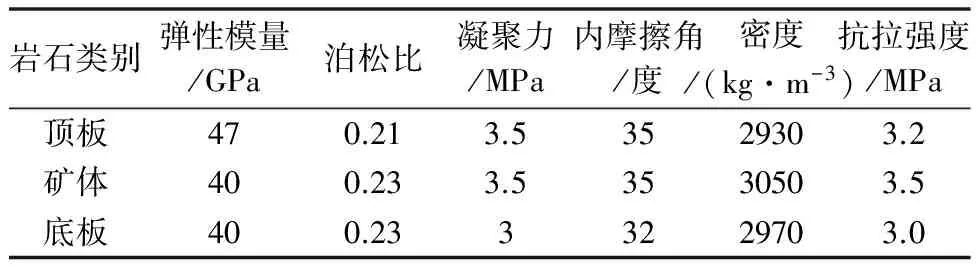
表1 巖體力學參數取值

2.2初始條件與邊界設置

2.2.1 初始地應力場

原巖應力是巖土工程數值模擬計算中的一個基本參數。其數值的大小，尤其是水平應力與垂直應力的比值，對計算結果的影響往往大于計算模型等因素的影響。因此，確定原巖應力是計算分析中的一個基本問題。一般來說，原巖應力大小和方向的確定，有效的方法是進行現場實測。由于沒有進行現場地應力測試，初始地應力場僅按自重應力場考慮。根據彈性原理，豎向應力σv=γH，水平應力σh=kσv。其中：γ為巖體容重，H為埋深；k為側壓力系數，k=v/(1-v)；v為泊松比。

2.2.2 靜力計算邊界條件

靜力分析過程中采用位移邊界條件，由于采動的影響范圍有限，離采場較遠處巖體位移值很小，將模型邊界處位移視為零，即在計算模型的左右(X方向)邊界、前后(Y方向)邊界和底邊界(Z=0)均施加位移約束條件，上邊界為自由邊界。模型頂部距離地面的平均距離為200 m，將模型上方巖體的作用轉化成面力垂直向下施加在模型的上部(Z=200)。

2.2.3 動力計算邊界條件

在進行動力分析時，合理設置模型周圍的邊界條件是非常重要的，因為在邊界上會產生波的反射影響，在一定程度上會對動力分析模擬的結果產生較大影響。如果把計算模型設置的很大，雖然可以消除反射波的影響，分析結果也會得到很大的改善，但是較大的計算模型會導致單元數與節點數增多，從而使計算時間大大增加。FLAC3D提供了靜態(黏性)和自由場兩種邊界條件設置來減小波在模型邊界上反射[61]。自由場邊界一般應用于地面結構的動力分析，考慮到采空區位于地表以下位置，因此本次計算模型動力分析在底邊界和側向邊界(包括X方向和Y方向)設置黏性邊界條件來吸收邊界上的入射波。上方采空區的底板設置為動荷載邊界，其他采空區邊界均設為自由邊界。

2.3力學阻尼與中心頻率的選取

采用FLAC3D求解動力方程的方法可解決準靜力問題和動力問題兩類力學問題。在這兩類問題中都要使用阻尼，但準靜力問題需要更多的阻尼使得動力方程能夠更快的收斂平衡。對于動力問題中的阻尼，需要在數值模擬中重現自然系統在動荷載作用下的阻尼大小。阻尼的存在使得能量產生了消耗，并且引起質點位移和速度的衰減。在動力分析中，FLAC3D提供了瑞利阻尼、局部阻尼和人工粘滯阻尼3種形式[61]。常用臨界阻尼值范圍一般在2%～10%。對于巖土材料而言，在進行動力計算時多數能量耗散在塑性流動階段，因此在進行大應變的動力分析時只需設置一個較小的阻尼比即可。本文采用的是瑞利阻尼。對于比較簡單的模型可用自振頻率作為瑞利阻尼的中心頻率，通過重力作用下無阻尼的自振計算求得。本文計算模型中心頻率取為30 Hz，阻尼比取5%時系統振幅方能得到較好的減弱。經測試，地震波在0.3 s后完成基本衰減，故系統模型受動態擾動時間選取0.3 s。

2.4爆破震動載荷的施加

在FLAC3D動力計算中，動載荷輸入可以采用加速度時程、速度時程、位移時程和應力時程4種不同方式，若采用粘滯邊界條件，則必須輸入速度時程進行分析。數值計算中可以將施加的爆破地震荷載簡化為諧波的形式或者簡化為三角形荷載的形式。根據第四章的理論分析，本章采用諧波形式的應力激勵動荷載模型，并將簡化后的諧波動荷載施加于上方采空區的底板，沿Z軸負方向傳播，進行爆破動荷載作用下采空區頂板動力響應狀況計算，包括應力、位移及塑性區的變化與分布情況。

2.5計算方案與監測點

為研究豎上下交疊采空區隔層頂板在開挖形成的靜力荷載以及爆破震動荷載作用下的穩定性分析采空區頂板在不同振幅、不同頻率的爆破震動荷載作用下的動力響應變化規律設計了以下4種計算方案：a 初始應力條件下對礦體模型上下兩個空區同時進行開挖，計算至靜力平衡，得到采空區隔板在自重靜荷載作用下的應力、位移及塑性區并監測隔層頂板下表面中間部位應力和位移變化；b 在爆破地震波荷載峰值為1 MPa時，頻率分別為20，50，100 Hz的不同地震波頻率下隔層頂板的動力響應；c 在頻率為50 Hz，地震波荷載峰值分別為0.5，1，1.5，2 MPa時的動荷載作用下頂板的動力響應規律；d 隔層頂板在頻率為100 Hz，動荷載峰值為0.5 MPa的爆破動荷載作用下的響應。

由固體力學理論可知，在自重和動荷載作用下采空區頂板的最大位移發生在空區間隔板的底部中心位置。所以為研究采空區隔板在爆破荷載作用下的動力響應變化規律，選取隔板中間豎直方向截面上的節點作為位移和應力的跟蹤監測點，在隔板厚度為10 m時該點在模型上的坐標為(145,1,73)。

整個計算過程分二步進行。先進行靜力分析，然后在此基礎上再施加動力荷載進行動力問題的分析。在第1步靜力分析前，先關閉動態分析模式，在模型邊界施加水平和豎直方向應力，形成初始地應力場，然后將采空區一次性開挖并計算至平衡狀態，分析采空區頂板在靜荷載作用下的變形，并將其圍巖靜態應力場結果作為第2步動態擾動的初始應力場。第2步輸入動力荷載簡化為諧波形式的應力激勵施加于模型上部空區底板沿Z軸負方向傳播，分析其在爆破荷載作用下的動態響應特征。

3 模擬結果分析與討論

FLAC在分析輸出的應力結果時，他給出的最大主應力，實際上是最小主應力，最小主應力實際上是最大主應力，用這兩個應力指標，可表征地壓活動在介質應力狀態變化方面產生應力集中或應力松馳的程度。且負應力為壓應力，正應力為拉應力。根據以上設置建立的模型首先進行原巖應力計算，然后對礦體開挖進行靜力計算，開挖后頂板在靜荷載作用下的最大主應力云圖、最小主應力云圖、豎直方向位移云圖以及拉伸剪切破壞區域如圖2所示。監測點的應力和位移隨開挖過程變化的關系見圖3。

從圖2和圖3可以看出：采空區開挖后圍巖原始應力平衡被打破，引起應力重分布和局部應力集中，并產生了向采空區方向的位移。在上部采空區的頂板處和下部采空區的底板處均出現較大的拉應力，在空區邊界和拐角處出現拉伸剪切破壞區，隔板比較完好中間未出現拉伸破壞區域。當頂板巖體達到再次平衡時，在底部中心處產生的位移和拉應力分別為2 mm、0.85 MPa。

圖2 開挖后隔層頂板的位移和應力云圖及塑性區

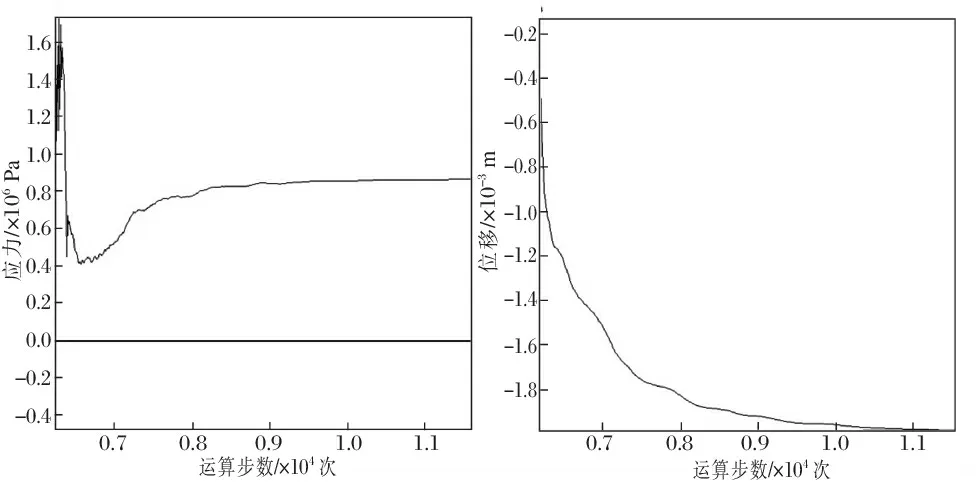
圖3 監測點的應力和位移隨開挖過程變化曲線

圖4分別為在荷載峰值為1 MPa，頻率分別為20，50，100 Hz的爆破動荷載作用下隔層頂板的最大主應力和豎向位移局部放大云圖。

圖4 頂板在不同頻率動荷載作用下的最大主應力和位移云圖

圖5分別為在荷載峰值為1 MPa，頻率分別為20，50，100 Hz的爆破動荷載作用下隔層頂板底部監測點的位移和應力隨動力計算時間的變化曲線。

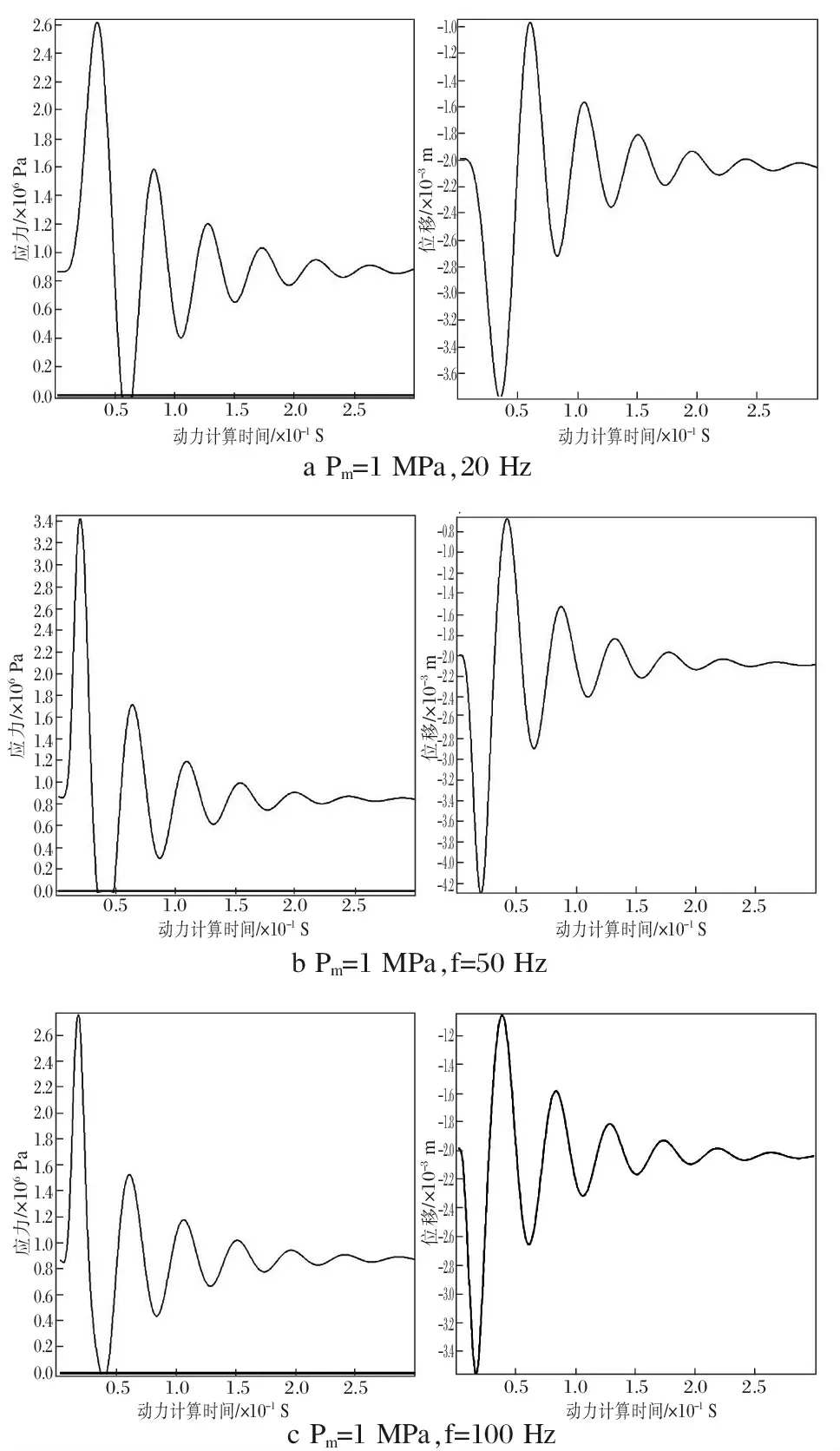
圖5 頂板在不同頻率動荷載作用下的動力響應曲線

從圖4和圖5可以看出：在爆破荷載峰值相同，頻率不同的爆破地震波作用下，隔層頂板的動力響應也不同。頂板的動力響應隨著頻率的增加先增大后減小，爆破地震荷載頻率越大，頂板產生的動拉應力和動位移越小。當頻率為50 Hz時頂板的動力反應最大，說明50 Hz頻率的爆破地震波對采空區頂板的穩定在影響最大，隔層頂板結構的固有頻率與爆破地震波的頻率接近，產生共振效應，可能使頂板發生突然失穩破壞。

圖6分別為在荷載峰值為0.5 MPa，頻率50 Hz的動荷載作用下隔層頂板最大主應力和豎向位移局部放大云圖以及隔層頂板底部監測點的位移和應力隨動力計算時間的變化曲線。

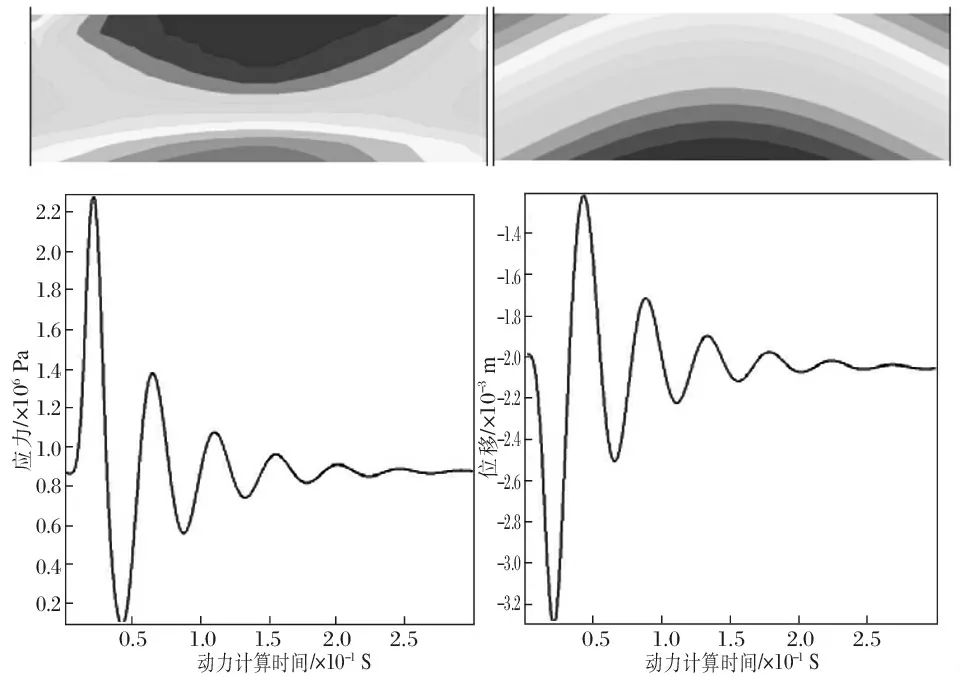
圖6 頻率為50 Hz，荷載峰值為0.5 MPa時頂板的動力響應規律

圖7分別為在荷載峰值為0.5 MPa，頻率100 Hz的動荷載作用下隔層頂板最大主應力和豎向位移局部放大云圖以及隔層頂板底部監測點位移和應力隨動力計算時間的變化曲線。

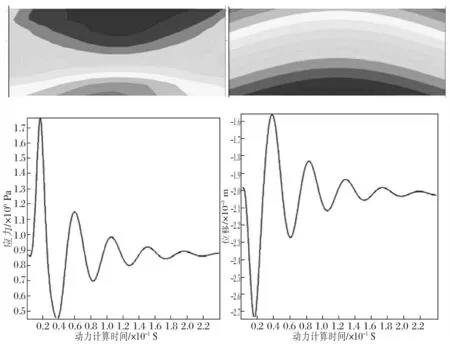
圖7 頻率為100 Hz，荷載峰值為0.5 MPa時頂板動力響應規律

圖8是在頻率為50 Hz，地震荷載峰值分別為0.5，1，1.5，2 MPa時的隔層頂板塑性區變化。

從圖8可以看出：在不同的爆破地震荷載強度作用下頂板的動力破壞程度不同，爆破荷載峰值越大，頂板的動力響應就越大，產生的拉應力也越大。當動荷載峰值為0.5 MPa時，只有隔層頂板上下空區的邊界出現塑性區，而當荷載峰值大于1 MPa時隔層頂板受到的拉應力大于其抗拉強度，底部中間區域首先發生拉伸破壞，開始出現小范圍塑性區，并隨著爆破荷載峰值的增大，頂板發生拉伸破壞的范圍也越大，并且破壞區域的形狀為拱形。

圖8 不同動荷載峰值作用下頂板塑性區變化規律

為了更清楚的觀察爆破地震波的頻率和振動幅值對頂板動力響應的規律，提取監測點在不同頻率不同荷載幅值下的最大拉應力變化值，并將其導入到Matlab中繪制出頂板的動力響應與爆破荷載及頻率的關系曲線如圖9所示。

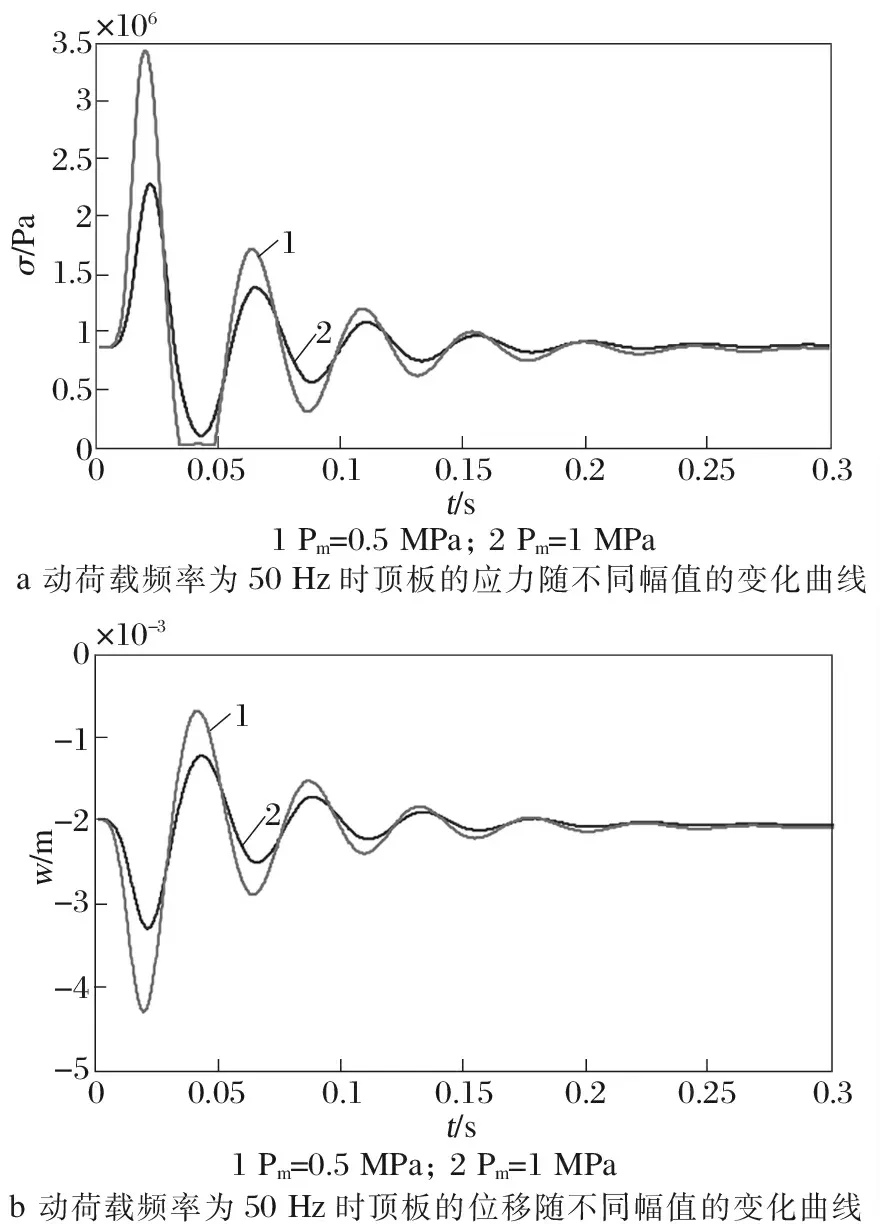
圖9頂板的動力響應與爆破荷載及頻率的關系

從圖9可以清晰的看出：采空區隔層頂板在不同頻率、不同荷載峰值的地震波作用下的應力變化過程。從以上數值模擬分析可以得出以下結論：爆破地震荷載峰值大小對采空區隔板穩定性的影響最明顯，隔板最大位移和最大拉應力隨峰值增大而增大，當動荷載峰值超過1 MPa時隔板底部中心部位開始出現拉伸破壞區，并且動荷載峰值越大破壞區域越大；隨頻率的增大，隔板最大位移和最大應力先增大后減小，當爆破荷載頻率接近頂板的固有頻率時，頂板產生的動力反應達到最大值，即50 Hz頻率的動荷載對采空區隔板的穩定性最不利。

4 結 論

本文以上下交疊地下礦山采空區隔層頂板為研究對象，采用數值模擬方法對采空區頂板在爆破震動作用下的動力響應進行了數值模擬研究。應用FLAC3D計算軟件，建立豎向排列的采空區模型。首先模擬出空區開挖以后在靜力載荷下頂板的位移和應力變化情況，并在靜荷載作用的基礎上對模型施加不同峰值的爆破動荷載，對頂板在動靜荷載共同作用下的位移場、應力場和塑性區的響應進行了研究，通過對比不同爆破荷載峰值情況下采空區頂板的動力響應來分析對穩定性的影響程度，揭示了動靜荷載共同作用下豎向排列采空區隔層頂板失穩破壞機理。

[1] 劉亞群, 李海波. 爆破荷載作用下黃麥嶺磷礦巖質邊坡動態響應的UDEC模擬研究[J]. 巖石力學與工程學報, 2004, 23(11): 42-45.

[2] 陳占軍, 朱傳云, 周小恒. 爆破荷載作用下巖石邊坡動態響應的FLAC3D模擬研究[J]. 爆破, 2005, 22(4): 8-15.

[3] 逄煥東, 陳士海. 彈性介質中爆破地震波傳播的分區變化規律研究[J]. 振動與沖擊, 2009(3).

[4] 閆長斌, 徐國元, 李夕兵. 爆破震動對采空區穩定性影響的FLAC3D分析[J]. 巖石力學與工程學報, 2005, 8(16): 2894-2899.

[5] Khandelwal M, Singh T N. Prediction of blast induced ground vibrations and frequency in opencast mine: A neural network approach[J]. Journal of sound and vibration, 2006, 289(4): 711-725.

[6] 傅洪賢, 趙勇, 謝晉水, 等. 隧道爆破近區爆破振動測試研究[J]. 巖石力學與工程學報, 2011, 30(2): 335-340.

[7] 吳姍, 陳何, 孫宏生, 等. 大紅山銅礦束狀孔采礦及爆破振動監測技術[J]. 有色金屬工程, 2015, 5(5): 126-129.

[8] 劉波, 韓彥輝. FLAC原理,實例與應用指南[M]. 北京: 人民交通出版社, 2005.

AStudyonNumericalSimulationofDynamicResponseofRoof

LIANG Chao

(FacultyofLandResourceEngineering,KunmingUniversityofScienceandTechnology,Kunming,Yunnan650093,China)

The roof of mined area is relatively weak, and the goaf roof is one of the most serious accidents in underground metal mines. The underground workers will not only pose a threat to the safety, but also have a significant impact on the production and management of underground pressure. There are many factors to affect the goaf roof stability. The stress distribution and the blasting vibration are the two most important factors. This paper mainly uses the method of theoretical analysis to be combined with numerical simulation, from static and dynamic two aspects of goaf roof stability of the stress in the weight and load of blasting under dynamic loads. The main contents of the thesis are the following: using the elastic vibration theory of thin plate down the top plate under uniform harmonic pulse displacement under load to calculate formulas for stress analysis. The damping, including the dynamic load strength, influence of dynamic frequency response of roof strata, and the dynamic response in the empty mining district under dynamic and static loads of roof are all analyzed.

Blasting earthquake wave; Roof of mined void; Dynamic response; Numerical simulation

2016-07-24

梁超(1991-)，男，寧夏石嘴山市人，在讀碩士研究生，研究方向：安全工程，手機：18695200970，E-mail：376677756@qq.com.

TD327.2

：Adoi：10.14101/j.cnki.issn.1002-4336.2016.04.019