輸電線路元件的結構可靠度分析

徐 彬，王松濤，曾二賢，吳海洋（中南電力設計院，湖北 武漢 430071）

?

輸電線路元件的結構可靠度分析

徐 彬，王松濤，曾二賢，吳海洋
（中南電力設計院，湖北 武漢 430071）

摘要：為正確評價輸電線路的安全性，本文以輸電線路元件（導地線、絕緣子和金具）作為分析對象，建立了可靠度分析模型，通過分析影響輸電線路元件荷載效應的永久荷載、風荷載的計算公式以及分布曲線，得到荷載效應的統計參數；考慮材料性能不定性、幾何參數不定性和計算模式不定性，得到抗力統計參數。采用一次二階矩方法，計算得到輸電線路元件在大風工況下的可靠度指標。結果表明，按現行輸電線路規范的安全系數設計的輸電線路元件，其可靠度水平較高。研究結果可為輸電線路概率極限狀態設計方法提供參考

關鍵詞：輸電線路；元件；可靠度指標。

輸電線路體系是高負荷電能輸送的載體，近年來逐漸趨于向大型化復雜化方向發展。導地線、絕緣子和金具作為輸電線路系統的一部分，其可靠性直接決定了整個輸電系統的安全性及穩定性。對于輸電線路的可靠度分析，目前國內外形成了一些有價值的成果。但以往較多的研究注重于桿塔結構分析，而對于輸電線路元件導地線、絕緣子和金具的結構可靠度分析，則鮮見于文獻。

本文建立了輸電線路元件的可靠度分析模型，通過分析影響荷載效應的永久荷載、風荷載的計算公式以及分布曲線，得到荷載效應的統計參數；考慮材料性能不定性、幾何參數不定性和計算模式不定性，計算得到抗力統計參數。采用一次二階矩方法，計算得到輸電線路元件在大風工況下的可靠度指標。考慮到目前輸電線路的安全性和穩定性愈加重要，為適應我國電力建設事業發展的需要，開展輸電線路元件的可靠性研究很有必要且具有實踐意義。

1 可靠度分析模型

1.1 現行規定GB 50545—2010中的計算公式

GB 50545—2010《110 kV～750 kV架空輸電線路設計規范》規定了輸電線路元件各自的設計表達式，可統一按式（1）表達：

式中：K為設計安全系數；Tp為承載力；Tmax為最大拉力。

1.2 極限狀態方程

輸電線路元件的工作狀態可以統一用抗力R與作用效應S表示為：

隨著R和S的變化，功能函數Z有三種變化：當Z＜0時，表示結構處于失效狀態；當Z＞0時，表示結構處于可靠狀態；當Z=0時，表示結構處于極限狀態。

考慮到荷載由永久荷載和可變荷載組成，式（1）的設計表達式可按下式表示：

則計算輸電線路元件可靠度的功能函數為

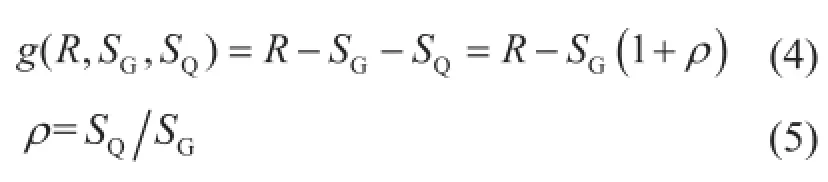
式中：ρ為荷載效應比值；SGK為永久荷載作用效應標準值；SQK為可變荷載作用效應標準值；SG為永久荷載作用效應；SQ為可變荷載作用效應。

2 基本變量的統計分析

2.1 荷載的統計分析

2.1.1 永久荷載的統計參數

輸電塔結構永久荷載包括導線及地線、絕緣子及其附件和結構構件及桿塔上各種固定設備等的重力荷載。與一般的民用建筑永久荷載有所差別，GB 50068—2001《建筑結構可靠度統一標準》中永久荷載統計特性是基于民用樓房統計數據得到，若直接引用將有失偏頗。而目前尚無輸電塔結構永久荷載統計數據，為此可進行如下處理，桿塔組件自重按式（6）表示：

式中：鋼材重度γ以及構件長度l變異性較小，而目前有對鋼構件截面幾何特性的大量統計，截面特性統計參數均值系數以及變異系數為KA=1.00，VA=0.05。所以自重荷載統計參數主要由截面特性控制，由此取KG=KA=1.00，VG=VA=0.05。

2.1.2 導地線風荷載的統計參數

GB 50545—2010規定，導地線風荷載標準值為：

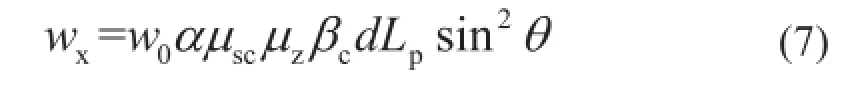
式中：wx為垂直于導線及地線方向的水平風荷載標準值；α為風壓不均勻系數；βc為導線及地線風荷載調整系數；μz為風壓高度變化系數；μsc為導線或地線的體形系數；Lp為桿塔的水平檔距；θ風向與導線或地線方向之間的夾角；W0為基準風壓標準值。參考已有文獻［6］，Wx的統計參數計算公式如下：

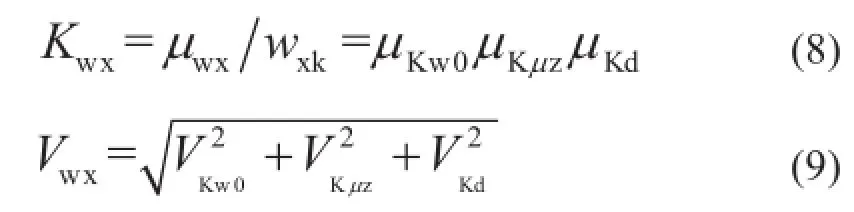
式中各參數取值見表1。

計算結果為：Kwx=0.467，Vwx=0.410。考慮設計基準期為100年，最大風荷載統計參數分別按KwT=1.154，VwT=0.166計算。

表1 統計參數取值

2.1.3 絕緣子風荷載的統計參數

GB 50545—2010規定，絕緣子風荷載標準值計算公式：

式中：wI為垂直于導線及地線方向的水平風荷載標準值；μz為風壓高度變化系數；AI為

絕緣子串承受風壓面積計算值；W0為基準風壓標準值。

另外，絕緣子的所承受的拉力主要來自導線張力，故絕緣子所承受的總的風荷載為：

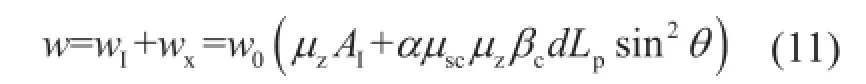
假設（dLp）/AI=e，則：

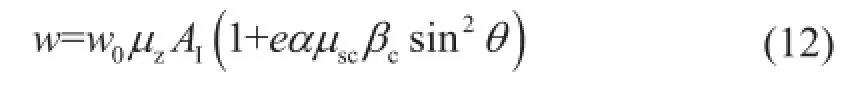
可把比值e看作定值，所以，絕緣子所受風荷載的統計參數（均值系數和變異系數），與導線所受風荷載的統計參數取值相同。

2.1.4 金具風荷載的統計參數

因為金具的所承受的拉力主要來自導線張力，故金具的荷載統計參數取用導地線荷載統計參數。

2.2 抗力的統計分析

2.2.1 導地線抗力的統計參數

由于缺少對導、地線抗力統計分析，考慮導、地線與拉索構件材料性能相似，故參考文獻［7］中拉索的統計參數，取三種類型拉索的抗力統計參數平均值：KR=1.28，VR=0.16。

2.2.2 絕緣子抗力的統計參數

本工程所使用的絕緣子含有復合絕緣子、玻璃絕緣子和瓷絕緣子，其中，盤型絕緣子為玻璃絕緣子。絕緣子種類繁多，且不同生產廠家質量水平也不相同，往往是通過試驗方法確定絕緣子抗力。由于缺少對絕緣子質量水平統計的資料，因此在進行可靠度分析工作中，參考已有相關研究及其有關文獻資料可知：各種絕緣子的機械強度服可用對數正態分布擬合，并且比額定負荷約高出50%，具有較高的機械強度，但強度變異性比較大，在15%～25%。故本文把絕緣子破壞負荷看作其抗力，把其與額定負荷之比m和抗力變異系數當作抗力隨機變量，進而分析絕緣子可靠度的變化規律。絕緣子抗力統計參數取值表見表2。

n取值：1.1、1.3、1.5和1.7；

v取值：0.10、0.15、0.20、0.25和0.30。

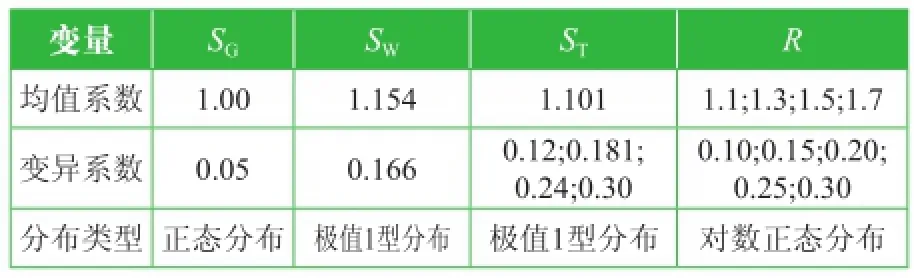
表2 絕緣子抗力統計參數取值

2.2.3 金具抗力的統計參數

由于有關金具抗力統計資料較為缺乏，考慮到其受力模式與軸心受拉構件較為接近。因此，對金具可靠度，金具抗力統計參數取4種情況均值水平。

根據《架空送電線路桿塔結構設計技術規定》DL 5154—2002，軸心受拉構件的設計表達式為：

式中：N為軸心拉力或軸心壓力設計值；m為構件強度折減系數；An為構件凈截面面積。對多排螺栓連接的受拉構件，要考慮鋸齒形破壞情況，f為鋼材的強度設計值。此時，構件抗力R可以表達為

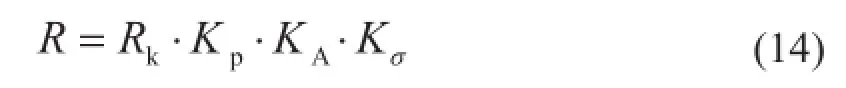
式中：Kp，KA，Kσ分別代表計算模式不確定性、截面幾何特性不確定性以及材料強度的不確定性。

根據誤差傳遞公式，此時構件抗力均值系數與變異系數可按下式計算：

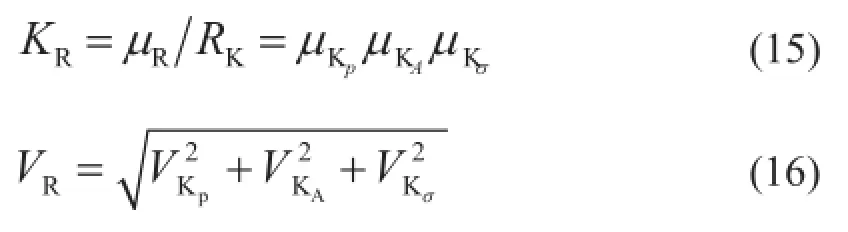
根據參考文獻［10］，按表3取值。

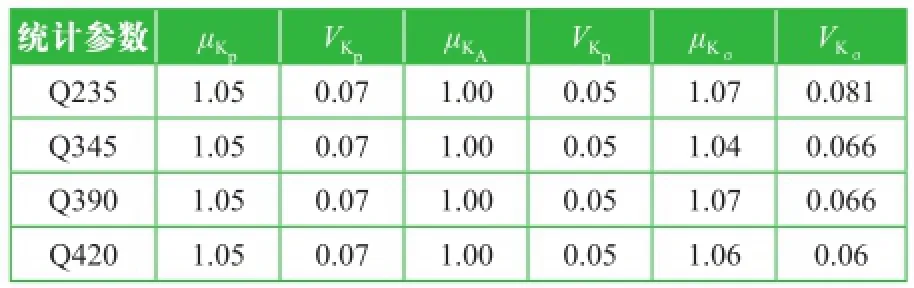
表3 統計參數取值

于是，對于不同種類的鋼材，可獲得抗拉抗力的統計參數見表4。

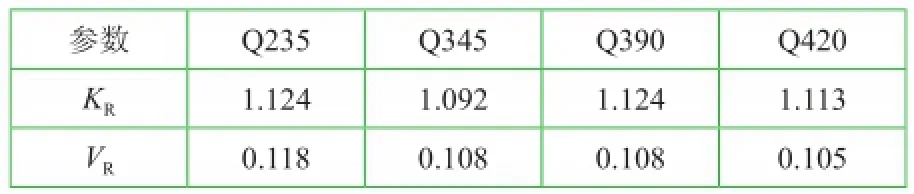
表4 軸心受拉構件抗力的統計參數

隨機變量統計參數見表5。

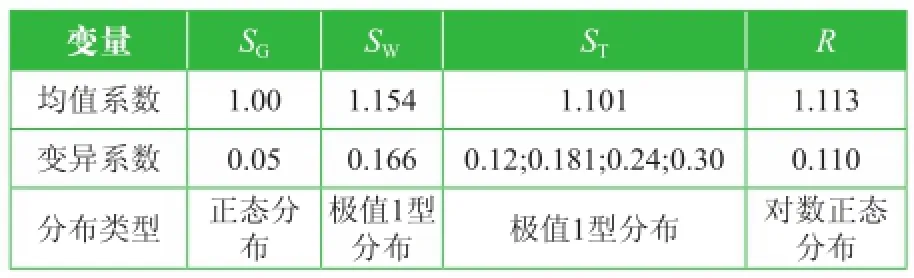
表5 金具隨機變量統計參數

3 可靠度分析結果

根據基本變量的統計參數，采用經典的一次二階矩法計算可靠指標。

3.1 導地線可靠度分析結果

導地線可靠度分析結果見表6，荷載效應比ρ影響見圖1。

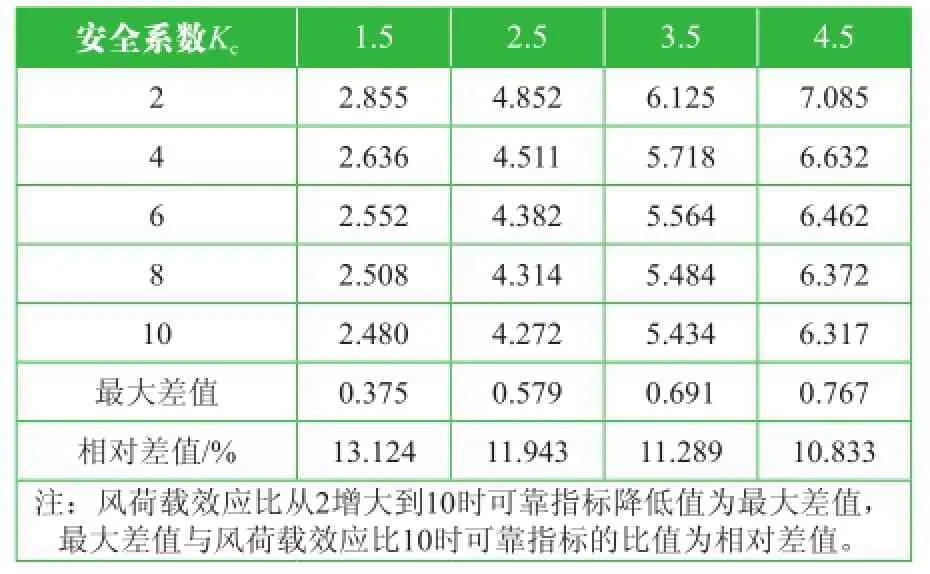
表6 安全系數Kc取值

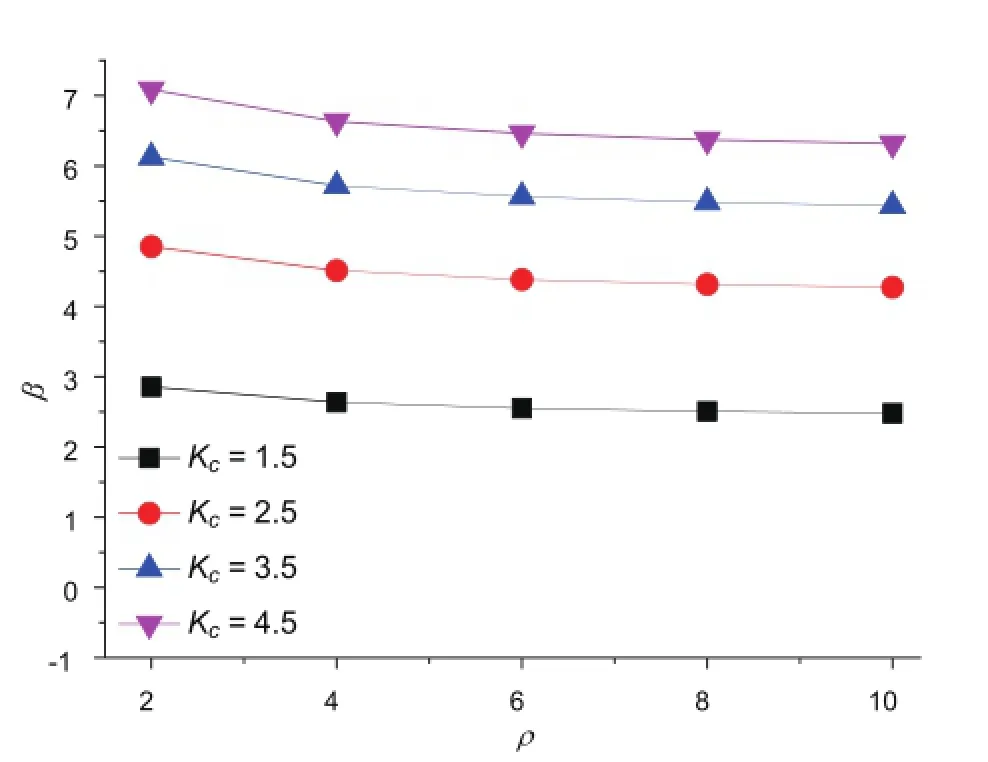
圖1 荷載效應比ρ影響

根據上述計算結果可知，隨著荷載效應比ρ的遞增，導地線的可靠指標不斷降低，且隨著安全系數的提高，影響逐漸減小。因此，荷載效應比亦是影響導地線可靠指標的主要因素。此外，不難發現，當安全系數取為2.5時，可靠指標均超過4.2。

3.2 絕緣子串可靠度分析結果

絕緣子串可靠度分析結果見圖2。

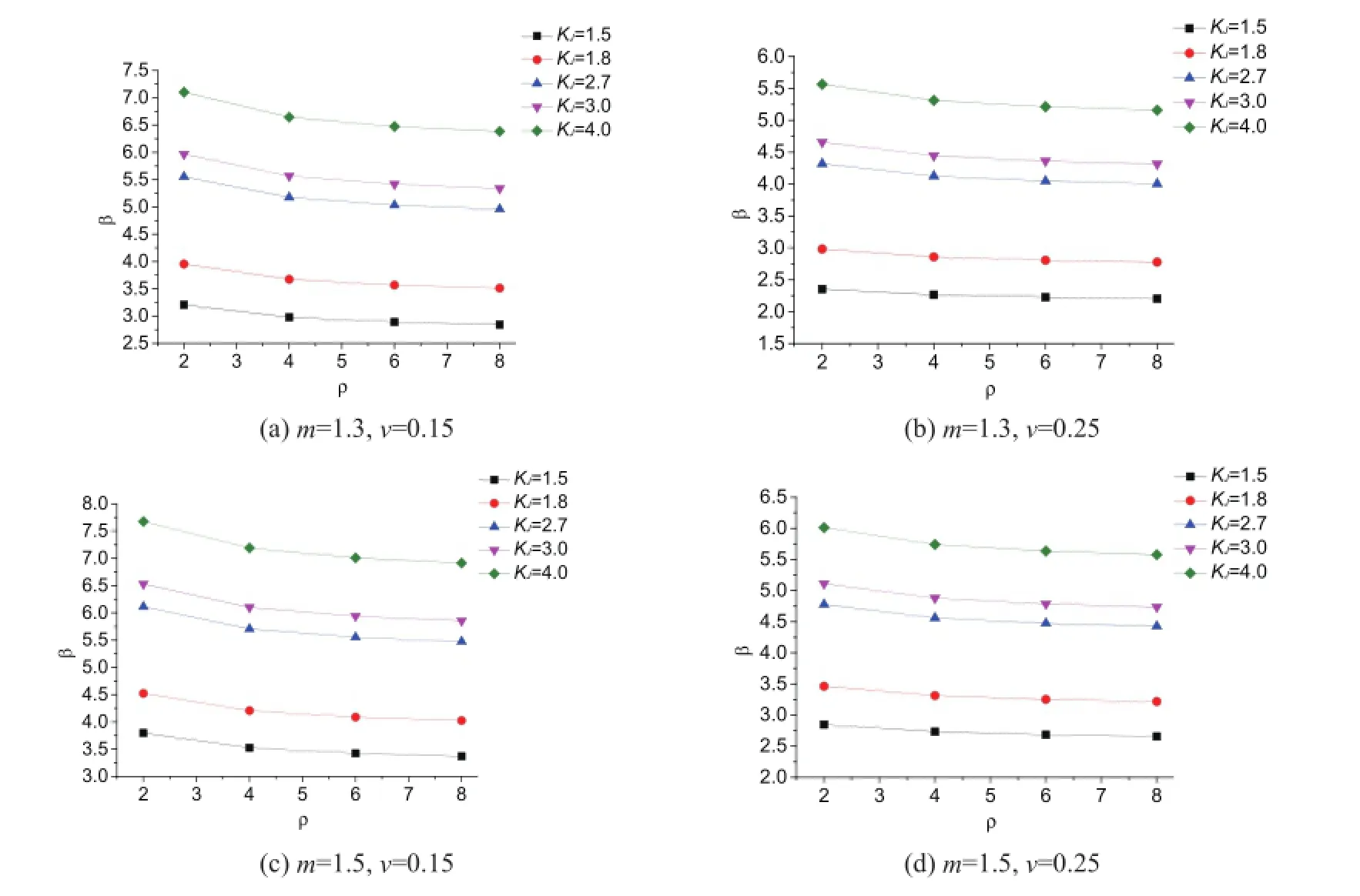
圖2 風荷載效應比ρ對可靠指標的影響

與前述構件可靠度的參數分析類似，荷載效應比對于絕緣子的可靠指標亦存在顯著影響，屬于必須要考慮的因素。且當安全系數取為2.7、m=1.3和v=0.25時，可靠指標均超過4.0。

3.3 金具可靠度分析結果

金具可靠度分析結果見表7和圖3。

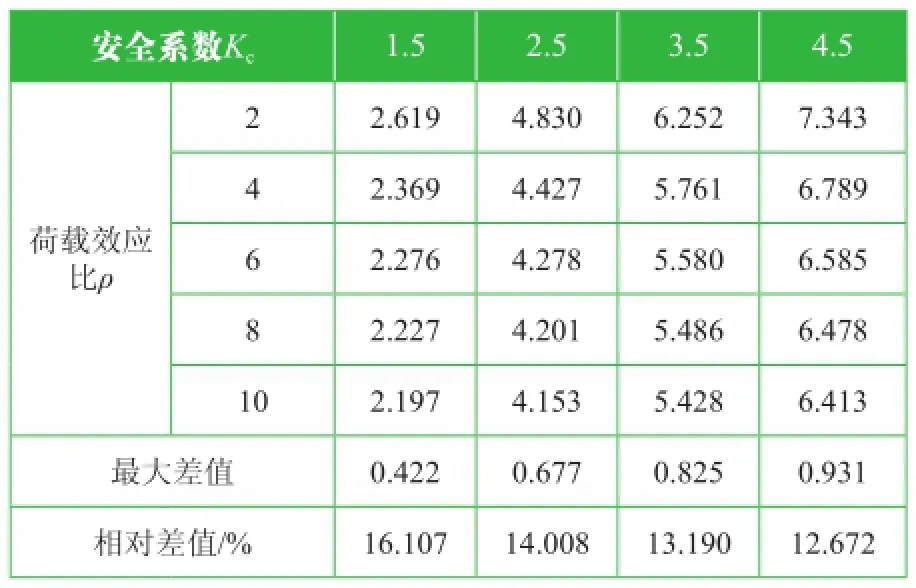
表7 金具可靠指標計算結果

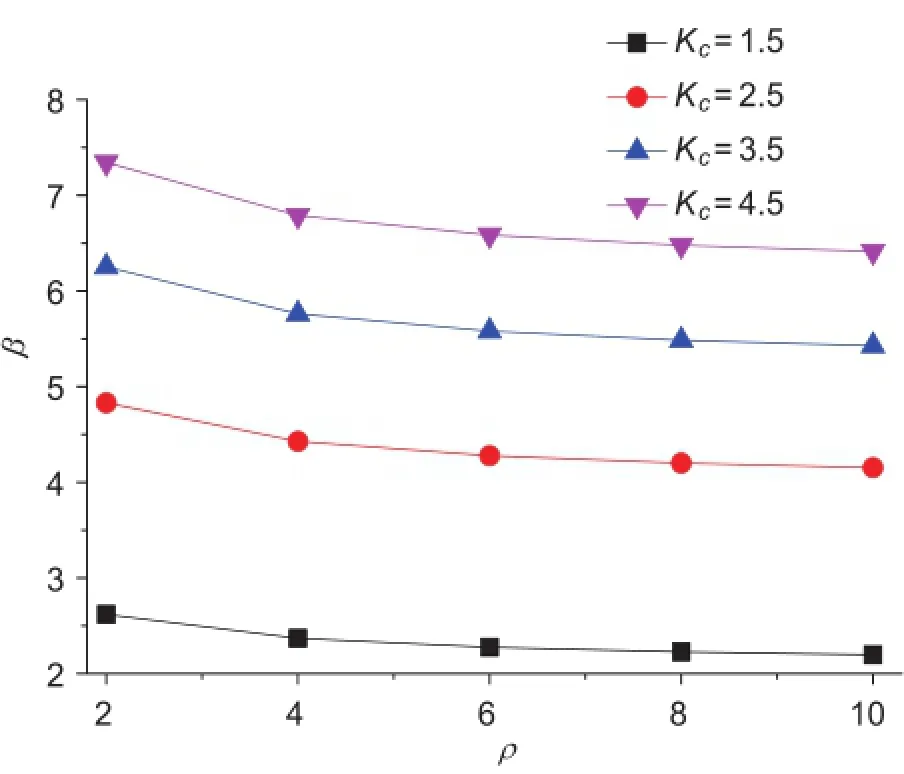
圖3 荷載效應比ρ影響

據上述計算結果可知，隨著荷載效應比ρ的遞增，金具的可靠指標不斷降低，且隨著安全系數的提高，影響逐漸減小。因此，荷載效應比亦是影響金具可靠指標的主要因素。此外，不難發現，當安全系數取為2.5時，可靠指標均超過4.1。

4 結論

通過建立輸電線路元件的極限狀態方程，采用一次二階矩法對輸電線路元件的可靠度進行計算分析。得到的主要結論如下：

（1）建立了導地線、絕緣子和金具的極限狀態方程。

（2）獲得了導地線、絕緣子和金具的荷載統計參數和抗力統計參數。

（3）在現有規范的安全系數下，導地線、絕緣子和金具在大風工況下的可靠度水平均較高，說明現行設計方法是較為安全的。

參考文獻：

［1］ 李茂華，李正，楊靖波.特高壓輸電線路桿塔可靠度研究［J］.電網技術，2010，34（5）.

［2］ 熊鐵華，梁樞果，鄒良浩.風荷載下輸電鐵塔的失效模式及其極限荷載［J］.工程力學，2009，26（12）.

［3］ 李致宇.大風覆冰條件下輸電桿塔可靠性模型的研究［J］.安全與環境工程，2010，17（3）.

［4］ GB 50545-2010，110 kV～750 kV架空輸電線路設計規范［S］.

［5］ GB 50068-2001，建筑結構可靠度統一標準［S］.

［6］ 歐進萍，段宇博.等效隨機靜風荷載的模型及其參數確定［J］.哈爾濱建筑工程學院學報.1994，27（2）.

［7］ 楊會杰，陳志華.預應力鋼結構拉鎖抗力的統計分析［C］.第七屆全國現代結構工程學術研討會，工業建筑，2007.

［8］ 邱志賢.絕緣子電氣機械特性的數理統計研究［J］.電磁避雷器，1976，（3）.

［9］ 張偉，等.基于概率統計的盤型懸式瓷絕緣子抽檢方法［J］.內蒙古電力技術，2011，29（4）.

［10］ 夏正中，鋼結構可靠度分析［J］.工業建筑，1981，（12）.

中圖分類號：TM75

文獻標志碼：B

文章編號：1671-9913（2016）01-0058-05

* 收稿日期：2015-04-28

作者簡介：徐彬（1987- ），男，湖北洪湖人，碩士，工程師，主要從事輸電線路結構和基礎設計研究工作。

Structural Reliability Analysis of Transmission Line Elements

XYU Bin， WANG Song-tao， ZENG Er-xian， WU Hai-yang
（Central Southern China Electric Power Design Institute， Wuhan 430071， China）

Abstract:For the correct evaluation of the safety of the transmission line， taking the transmission line elements （conductor & earth wire， insulator and hardware） as the analysis objects， the reliability analysis model was established，by analyzing the affecting factors of load effect of transmission line elements such as the calculation formula and distribution curve of permanent load and wind load， the statistical parameters of load effect were obtained； Considered the uncertainty of material properties， geometry and computational model， the resistance statistical parameters were obtained. Using a second-order moment method， calculated the reliability index of the transmission line element in maximum wind condition .Results show that the reliability level of the transmission line elements designed by current specification of safety factor was high. The calculation results can provide reference for the establishment of probability limit state design methods of the transmission line.

Key words:transmission line； elements； reliability index.