基于多目標遺傳算法的高速履帶車輛動力學模型參數修正研究

王欽龍，王紅巖，芮強（裝甲兵工程學院機械工程系，北京100072）

?

基于多目標遺傳算法的高速履帶車輛動力學模型參數修正研究

王欽龍，王紅巖，芮強
（裝甲兵工程學院機械工程系，北京100072）

摘要：為了提高高速履帶車輛多體動力學模型仿真結果的準確度，對模型參數修正方法進行了研究。建立了高速履帶車輛多體動力學模型，根據其行駛工況統計規律，選擇水泥路和砂石路作為參數修正的行駛路面條件。對比分析了模型參數修正前的仿真結果與實車測試結果，并給出了修正目標函數的表達式。通過正交實驗設計篩選出對目標函數影響較大的待修正模型參數。為了解決修正效率低、計算量大的問題，建立了修正參數與目標函數之間關系的徑向基神經網絡近似模型。通過分析目標函數隨修正參數的變化規律，采用多目標遺傳算法NSGA-Ⅱ對兩種工況條件下的模型參數同時進行修正，并確定了最終解。研究結果表明，動力學模型仿真結果的準確度得到了提高，證明該修正方法的有效性。

關鍵詞：兵器科學與技術；高速履帶車輛；參數修正；多目標遺傳算法；徑向基神經網絡

0　引言

由于虛擬樣機技術的多體動力學建模及仿真是當前研究高速履帶車輛行駛平順性、操縱穩定性以及越野機動性等動力學性能的一種重要方法［1-3］，而動力學性能分析結果是否可信直接取決于所建立的動力學模型的準確程度。在建模過程中，由于模型的簡化、參數測量誤差等因素的影響，所建立的多體動力學模型與實際車輛之間必然存在一定的差異，為了縮小這種差異，需要對車輛多體動力學模型的參數進行修正，從而提高其動力學性能分析結果的準確度［4］。

車輛多體動力學模型參數修正就是通過某種優化算法在參數設計空間中進行搜索，獲得使動力學模型的仿真結果與實車測試結果最接近的模型參數，從而提高模型仿真結果的可信性和準確度。

本文以某型高速履帶車輛為研究對象，根據其行駛工況的統計規律，分別選取車輛在水泥路和砂石路兩種典型路面并以30 km/h勻速行駛作為模型修正的工況條件。首先建立高速履帶車輛多剛體動力學模型，對比分析兩種工況條件下參數修正前的仿真結果與實車測試結果，初步驗證動力學模型的可信性并確定修正目標函數的表達形式；其次，利用正交實驗設計篩選出待修正的模型參數；為解決修正效率低、計算量大的問題，建立了待修正參數與目標函數之間關系的徑向基神經網絡近似模型；最后，通過分析目標函數隨修正參數的變化規律，采用多目標遺傳算法NSGA-Ⅱ對上述兩種工況條件下的動力學模型參數同時修正，獲得Pareto前沿并確定參數修正的最終解。相關技術流程如圖1所示。

1　高速履帶車輛多體動力學建模

1.1模型的拓撲結構分析

某型高速履帶車輛主要由上裝與車體系統、動力傳動系統和行動系統等組成，其中行動系統包括主動輪、負重輪、托帶輪、誘導輪及曲臂型張緊機構、履帶板、履帶銷及懸掛裝置彈性元件和阻尼元件等。建模時，主要以行動系統為主，其中，在保證履帶張緊力符合實際的前提下，張緊機構的傳動裝置簡化為滑柱和套筒，二者采用移動副和彈簧阻尼力進行約束，傳動裝置與車體、曲臂之間分別采用球副和圓柱副進行約束，曲臂與車體、誘導輪之間分別采用旋轉副進行約束，以保證張緊機構與誘導輪之間具有確定的運動關系。其他子系統與車體合并為一個剛體系統模型。首先根據部件之間的約束關系，對模型進行拓撲結構分析，如圖2所示，各部件和約束明細見表1和表2.

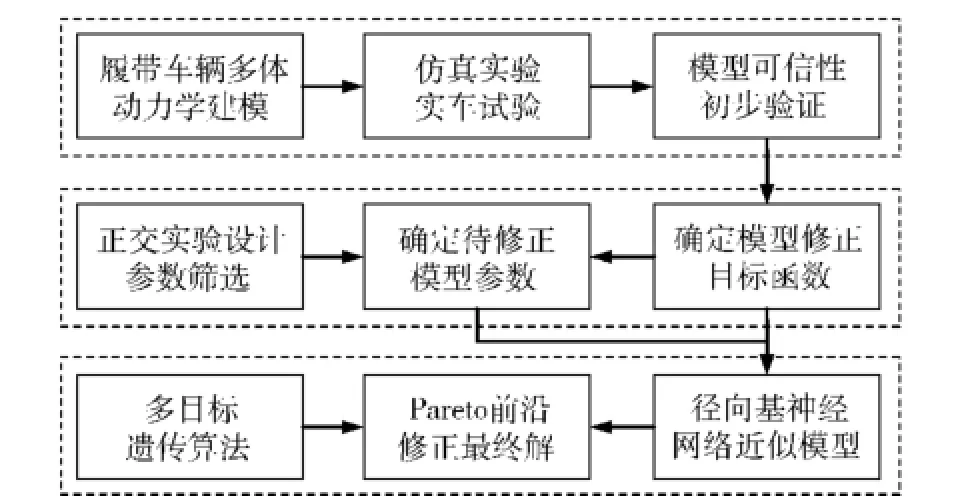
圖1　模型參數修正技術流程Fig.1 Updating process of model parameters

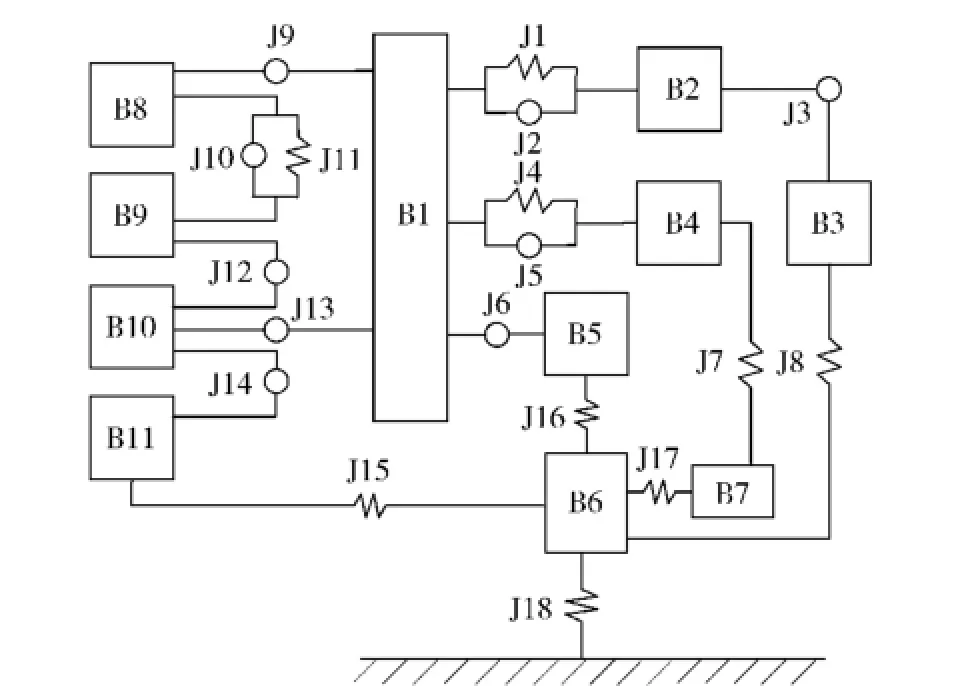
圖2　模型拓撲結構圖Fig.2 Topological structure of model

分析圖2、表1和表2可知，建立動力學模型共需部件數目為427，位移約束數目為54，其中旋轉副、球副、移動副和圓柱副限制自由度分別為5、3、5和4，模型總自由度數目為2 348.

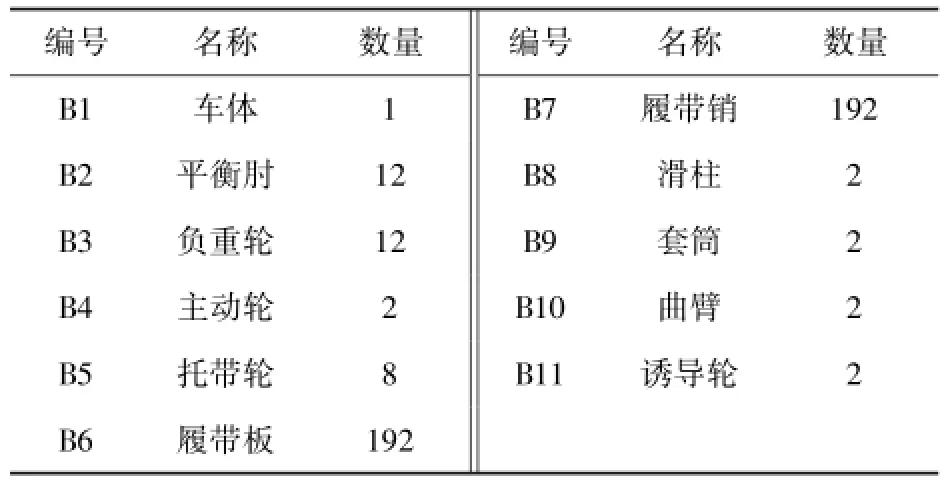
表1　部件明細表Tab.1 Parts list

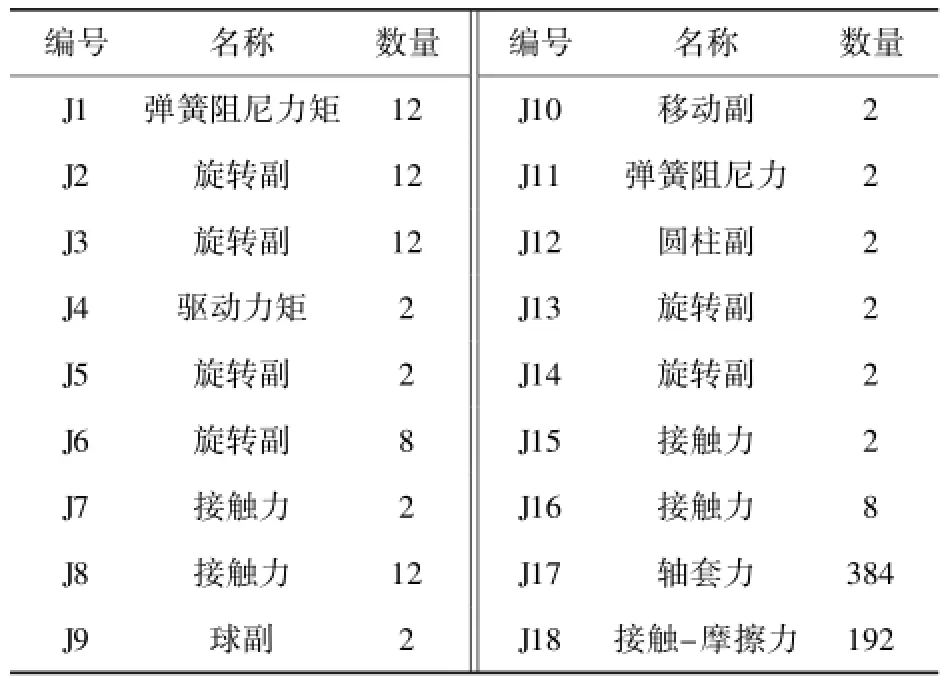
表2　約束明細表Tab.2 Constraint list

1.2力約束描述

在圖2中，約束J1為作用在平衡肘和車體之間的彈簧阻尼力矩，通過對懸掛系統的扭桿彈簧-葉片式減震器等效得到［5-6］，等效公式為

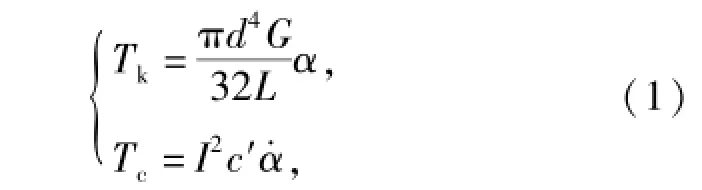
式中：Tk和Tc分別為等效彈簧力矩和等效阻尼力矩；d為扭桿彈簧直徑；G為扭桿彈簧剪切模量；L為扭桿長度；I為減震器拉臂至平衡肘安裝點的傳動比；c′為減震器阻尼系數；α為平衡肘轉動角度變化量，α·為其變化率。

在高速履帶車輛中，主動輪、負重輪、誘導輪及托帶輪與履帶間的相互作用力按接觸力處理，即約束J7、J8、J15和J16，其計算公式為

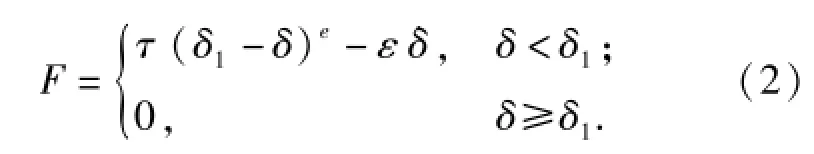
式中：″為接觸力；τ和ε分別為接觸剛度系數和阻尼系數；e為接觸力非線性指數；δ為接觸廣義距離，其變化率為；δ1為產生接觸力的臨界距離。

履帶板與地面之間的相互作用力按接觸-摩擦力約束處理，即J18，其中接觸力計算公式同（2）式，摩擦力計算公式為

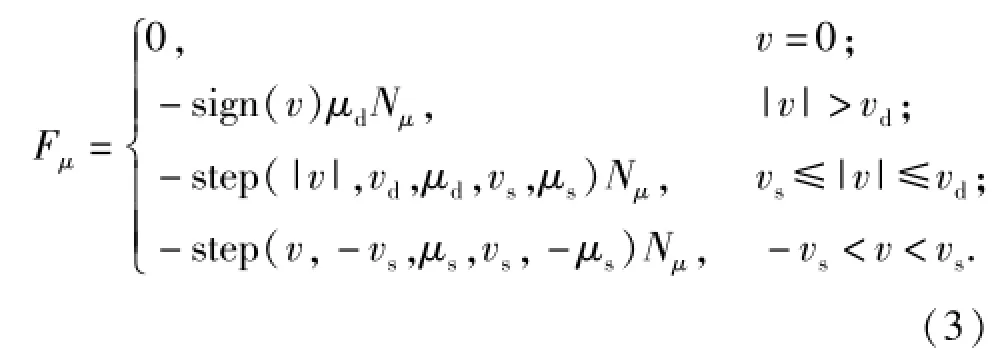
式中：″μ為摩擦力；v為履帶板與地面之間的相對滑動速度；vs為靜摩擦轉換速度；vd為動摩擦轉換速度；μs為靜摩擦系數；μd為動摩擦系數；Nμ為履帶板與地面間的正壓力。

主動輪驅動力矩約束J4根據具體工況條件進行定義，其余力約束（J11和J17）按線性彈簧阻尼力處理，計算公式較為簡單，限于篇幅，不再贅述。

1.3位移約束描述

動力學模型中任一部件廣義坐標可表示為

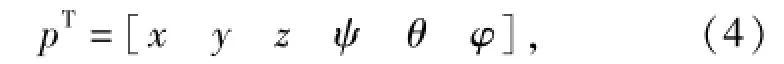
式中：x、y、z為笛卡爾坐標系下的部件質心坐標；ψ、θ、φ為質心坐標歐拉角。以模型中應用最多的旋轉副為例，對其進行位移約束描述，由于旋轉副限制3個方向的相對位移和兩個方向的相對轉角，因此，其位移約束方程可表示為

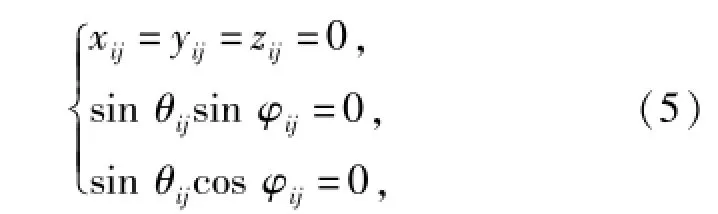
式中：xij、yij、zij為部件i相對部件j在3個方向的位移分量；ψij、θij、φij為部件i相對部件j的歐拉角。

1.4路面建模

高速履帶車輛行駛路面以砂石路和水泥路最具有代表性，是車輛的典型行駛路面，為了使模型參數修正結果具有較好的適應性和普遍性，本文選擇某車輛試驗場的水泥路和砂石路作為模型修正的行駛路面條件，根據國家標準GB7031的規定，對兩種路面實測路面譜進行擬合，路面譜擬合表達式為

式中：Gq（f）為路面不平度空間頻率f對應的功率譜密度；fl和fu分別為f的下限和上限；Gq（f0）為路面不平度參考空間頻率f0對應的標準功率譜密度，f0=0.1 m-1；w為頻率指數，是路面功率譜密度與空間頻率在雙對數坐標下的比例系數。根據（6）式，路面不平度可表示為

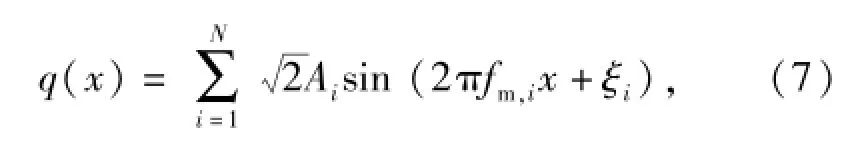
式中：q（x）為路面縱向距離x對應的路面不平度；ξi為N個在［0，2π］區間均勻分布的隨機數；fm，i為在［fl，fu］內劃分的N個區間所對應的中心頻率，每個區間長度為Δf；Ai為對應諧波的振動幅值，即

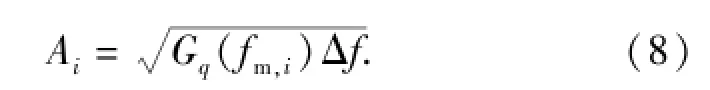
根據路面不平度序列，構造路面節點矩陣和單元矩陣，并生成代表水泥路和砂石路的動力學仿真路面模型［7］，如圖3所示。

圖3　隨機路面模型Fig.3 Simulation model of random road surface

1.5整車多體動力學模型

采用基于廣義笛卡爾坐標系的第一類拉格朗日方程建立高速履帶車輛多體動力學模型，系統廣義坐標矩陣為

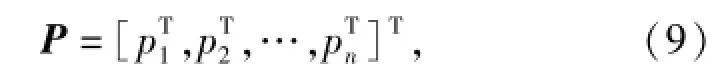
式中：n為模型部件數量。對于系統的約束矩陣方程可表示為

式中：m為系統位移約束和力約束方程數目。則動力學模型的歐拉-拉格朗日方程組［8］為

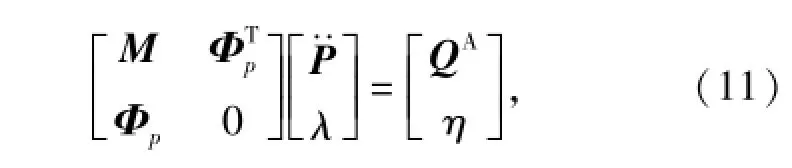
2　模型參數修正目標函數

2.1模型可信性初步驗證

在進行參數修正之前，需要對模型的可信性進行初步驗證，以保證后續修正計算初始點的準確度。為此，本文以在某車輛試驗場進行的高速履帶車輛行駛振動試驗為例進行研究工作，試驗路面選取前述水泥路和砂石路，行駛車速為30 km/h，測試信號為車體前甲板中央處的垂向振動加速度，動力學仿真工況條件與實車試驗一致。圖5和圖6分別為水泥路和砂石路上實車測試結果與動力學仿真結果的加速度功率譜密度曲線對比。

圖4　高速履帶車輛多體動力學模型Fig.4 High mobility tracked vehicle multi-body dynamic model

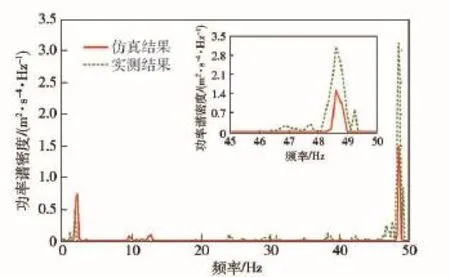
圖5　水泥路工況的加速度功率譜密度曲線對比Fig.5 Comparison of PSD curves under the condition of cement road

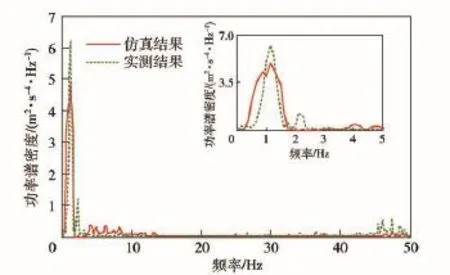
圖6　砂石路工況的加速度功率譜密度曲線對比Fig.6 Comparison of PSD curves under the condition of gravel road

由圖5可知，水泥路工況下實車測試結果與仿真計算結果的功率譜密度曲線主峰值均在48.5 Hz附近，而由該車履帶板節距tT和行駛車速u可知，來自履帶板節距的激勵頻率fT=u/tT=48.3 Hz，說明在水泥路面行駛時，車體振動的主要激勵源來自履帶板的激勵，由于水泥路的路面等級較高，路面不平度對車體振動的影響相對較小。

由圖6可知，砂石路工況下實車測試結果與仿真計算結果的功率譜密度曲線主峰值均在1 Hz附近，與車體的振動主頻率較為一致。對比圖5可知，由于砂石路的路面等級較低，車輛在砂石路面行駛時，車體振動的主要激勵源來自路面不平度的激勵，履帶板的激振對車體振動的影響相對較小。

綜上所述，本文建立的高速履帶車輛動力學模型具有一定的可信性，仿真結果較為真實地反映了實際車輛的動力學響應特性。

2.2模型參數修正的目標函數

由前述可知，實車測試結果與仿真計算結果的功率譜密度曲線比較相似，但仍然存在一定的差異。造成這種差異的來源主要有：一是建模時對部分設計參數進行了等效簡化；二是受加工誤差、測量誤差以及裝配誤差等因素的影響，設計參數本身就存在一定的不確定性。因此需要對模型參數進行修正，以提高仿真計算結果的準確度。

由于仿真計算用路面譜是實際路面譜的一致估計，具有較高的統計精度，因此不考慮由于路面譜差異所造成的仿真計算結果與實車測試結果的誤差。

參數修正的首要工作是建立修正目標函數，以量化實車測試結果與仿真結果的相似性。由于振動加速度功率譜密度曲線不僅反映了振動能量的總體大小，還反映了信號的頻率成分以及各頻率成分所對應振動能量的相對大小，因此，采用功率譜密度曲線構造參數修正的目標函數，即

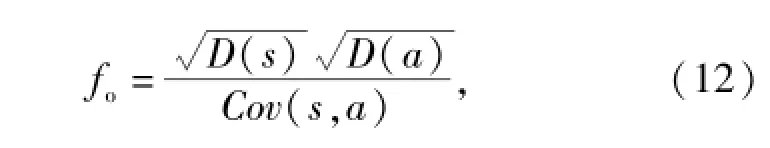
式中：s和a分別是仿真結果與實測結果的功率譜密度；D（s）和D（a）分別是仿真結果與實測結果的方差；Cov（s，a）是仿真結果與實測結果的協方差。fo的取值范圍為［1，∞］，函數值越接近1，則表示仿真結果越準確，與實車測試結果越接近。

3　模型修正參數篩選

為了確定對修正目標函數影響較大的參數，以縮小參數設計空間和提高修正效率，本文首先利用實驗設計進行參數篩選。根據車輛動力學的相關理論［9］，選取車體主慣量Ixx和Iyy、車體質心縱向位置cmx、車體質心垂向位置cmz、扭桿彈簧剛度系數（該車第1，2，5，6扭桿彈簧剛度系數與第3，4扭桿彈簧剛度系數不同，分別記為k1、k2）以及減震器的等效阻尼系數c進行參數篩選，車體質量一般認為是準確值，故不將其作為修正參數。為保證參數修正后，車體姿態和車底距地高變化不大，參數取值范圍設定在［-10%，10%］。

由于篩選參數較多，單次實驗仿真計算量較大，故采用L8（27）標準正交表進行7因子2水平正交實驗設計，對每組實驗參數組合進行動力學仿真，提取仿真結果并根據（12）式計算修正目標函數的響應值，最后計算各參數對應的極差以確定對目標函數影響較大的參數，極差K計算公式為

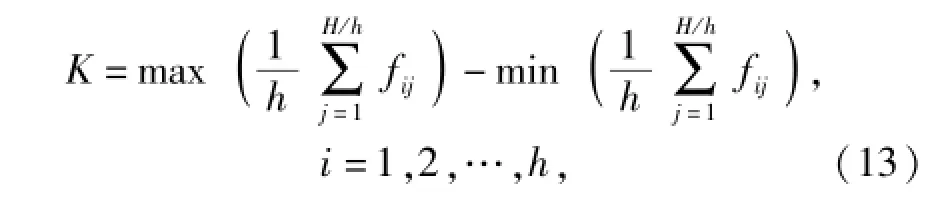
式中：H為實驗次數；h為因子水平數；H/h為每個因子水平的實驗次數；fij為因子第i個水平的第j次實驗所對應的目標函數響應值。不同因子的極差是不同的，極差越大，表明該因子對目標函數的影響程度越大。根據極差計算結果繪制柱狀圖如圖7所示。

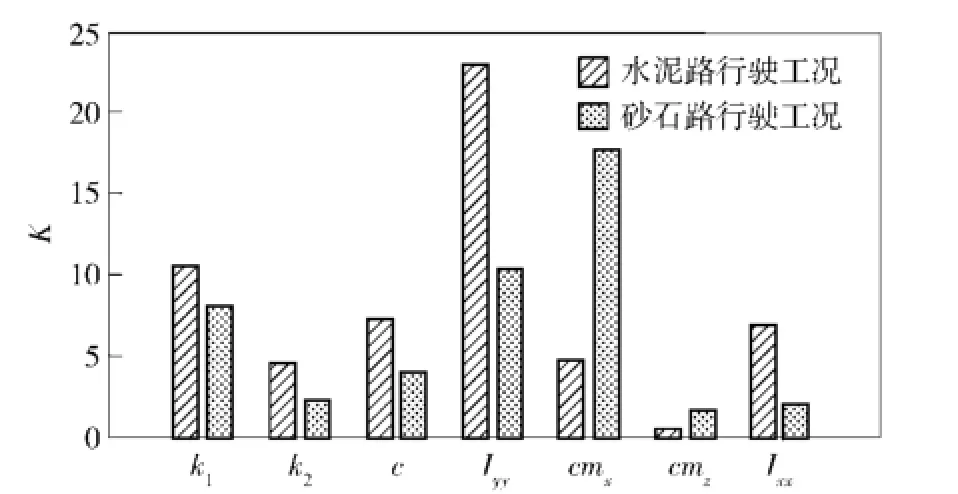
圖7　兩種路面工況條件下模型參數的極差Fig.7 Range of model parameters under two road conditions

由圖7可知：在水泥路工況條件下，對目標函數影響較大的參數依次是Iyy、k1和c；在砂石路工況條件下，對目標函數影響較大的參數依次是cmx、Iyy和k1.其中k1和Iyy對兩種工況條件下的目標函數影響程度均較大。由于在砂石路工況條件下，cmx的影響程度最大，而參數c的影響程度很小。因此，選取Iyy、k1和cmx作為兩種工況條件下的待修正模型參數。

4　徑向基神經網絡近似模型

4.1徑向基神經網絡近似模型

由于高速履帶車輛多體動力學模型的規模較大，仿真解算時間長、效率低，為解決這一問題，本文采用徑向基神經網絡構造了待修正參數與修正目標函數之間關系的近似模型，以替代動力學模型復雜的仿真計算，提高修正效率。

徑向基神經網絡［10-12］是一種高精度的多維空間非線性函數逼近技術，由輸入層、隱含層和輸出層構成，其中隱含層中神經元的變換函數即徑向基函數，是一種對中心點徑向對稱且衰減的非負非線性函數，其表達式為

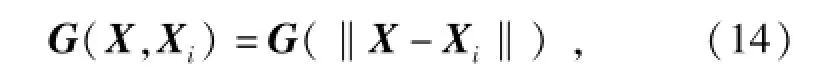
式中：X表示輸入向量；Xi為任一隱含層節點徑向基函數的中心點，一般選取自訓練樣本；‖X-Xi‖為歐幾里德范數，表示函數值僅與X和Xi之間的歐式距離有關，常采用多元高斯函數表示，即

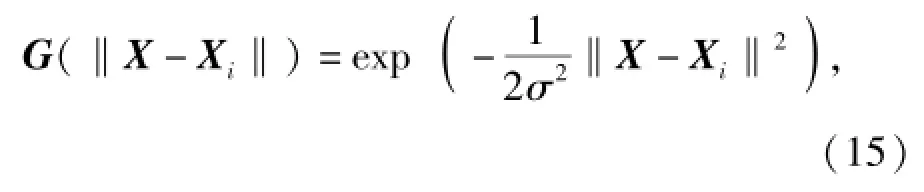
式中：σ2為高斯函數的方差。則徑向基神經網絡輸出層第j個神經元輸出為

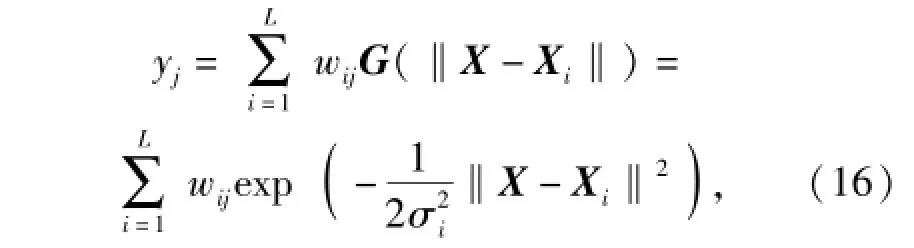
式中：wij為隱含層第i個節點與輸出層第j個節點之間的突觸權值；L為隱含層節點數目。則整個神經網絡輸出層的響應為

式中：W=［wij］為輸出權值矩陣；G為由（15）式組成的格林矩陣，具有旋轉不變性和平移不變性。則權值矩陣W可直接用偽逆的方法求解，即

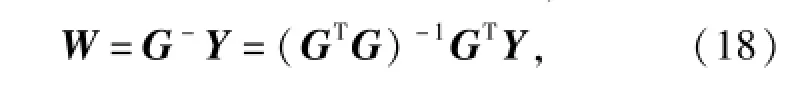
式中：Y為該神經網絡訓練樣本所對應的期望響應，在本文中，即用于建立近似模型的樣本點所對應的修正目標函數響應值。

求得權值矩陣W后，徑向基神經網絡訓練完成，即得到所求近似模型。

首先利用優化拉丁超立方實驗設計構造待修正參數的設計空間，參數取值范圍與參數篩選一致，一共得到32組修正參數組合，對每組參數組合進行動力學仿真并計算修正目標函數響應值，獲得用以訓練徑向基神經網絡的樣本組合，利用該樣本組合求取權值矩陣并得到修正參數與目標函數之間的近似模型，圖8～圖13為修正參數初始值處的近似模型，例如，圖8為參數k1初始值處的近似模型。

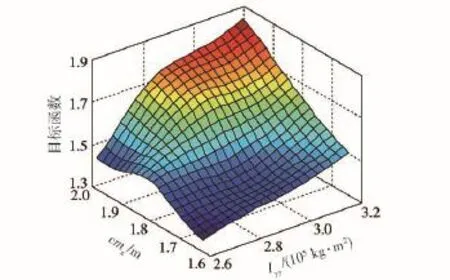
圖8　水泥路工況cmx、Iyy與目標函數的近似模型Fig.8 Approximation model of cmx，Iyyand objective function under the condition of cement road

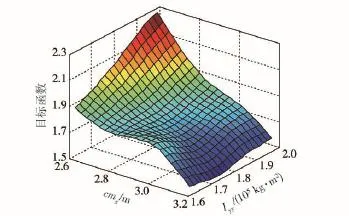
圖9　砂石路工況cmx、Iyy與目標函數的近似模型Fig.9 Approximation model of cmx，Iyyand objective function under the condition of gravel road

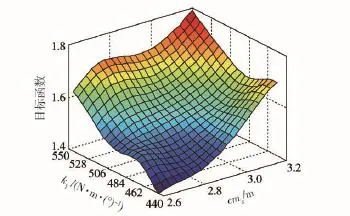
圖10　水泥路工況cmx、k1與目標函數的近似模型Fig.10 Approximation model of cmx，k1and objective function under the condition of cement road

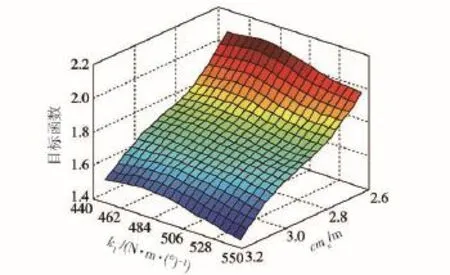
圖11　砂石路工況cmx、k1與目標函數的近似模型Fig.11 Approximation model of cmx，k1and objective function under the condition of gravel road

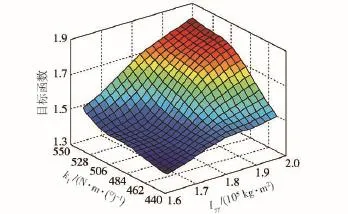
圖12　水泥路工況Iyy、k1與目標函數的近似模型Fig.12 Approximation model of Iyy，k1and objective function under the condition of cement road

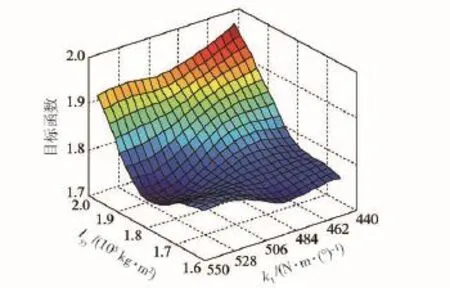
圖13　砂石路工況Iyy、k1與目標函數的近似模型Fig.13 Approximation model of Iyy，k1and objective function under the condition of gravel road

4.2近似模型擬合精度檢驗

在修正參數設計區間內隨機抽取15個樣本點，分別利用動力學模型和近似模型得到對應的目標函數真實值和預測值，如圖14和圖15所示。近似模型擬合精度指標通常采用復相關系數R2表示，即

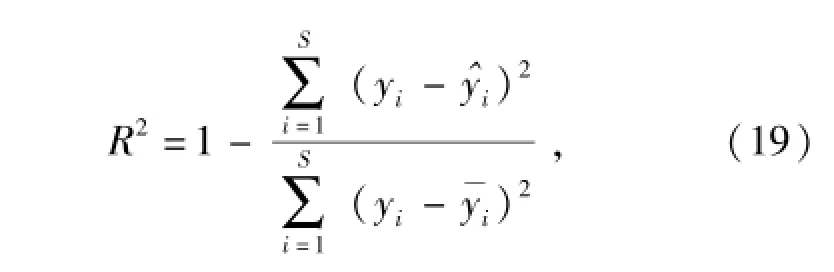
式中：yi為樣本點的真實值；為近似模型在樣本點處的預測值；為樣本點真實值的均值；S為擬合精度檢驗所用的樣本點個數。R2數值大小在［0，1］之間，一般要求近似模型的R2大于0.9才能滿足使用要求，R2越靠近1，則近似模型的擬合精度越高，預測值越準確。經計算，水泥路工況和砂石路工況的近似模型R2分別為0.964 2和0.978 7，說明構建的徑向基神經網絡近似模型的擬合精度較高，可滿足后續參數修正計算的需要。

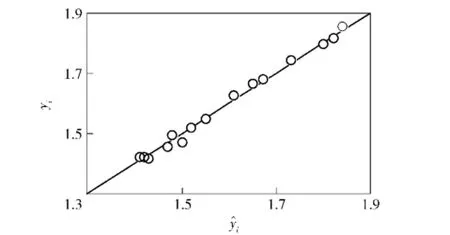
圖14　水泥路工況近似模型預測值與真實值對比Fig.14 Comparison of real value and predicted value of approximation model under the condition of cement road

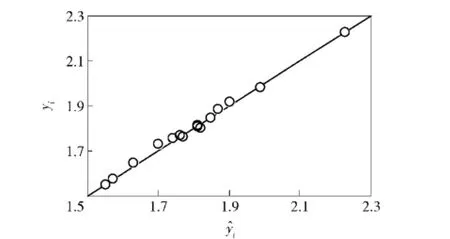
圖15　砂石路工況近似模型預測值與真實值對比Fig.15 Comparison of real value and predicted value of approximation model under the condition of gravel road

5　動力學模型參數修正

5.1目標函數隨修正參數的變化規律

分析上述近似模型可知，在整個設計空間內，修正參數與目標函數大致呈單調變化，為更加直觀地分析其變化規律，分別在修正參數初始值處選取目標函數隨其中一個參數的變化曲線進行分析，如圖16～圖18所示。

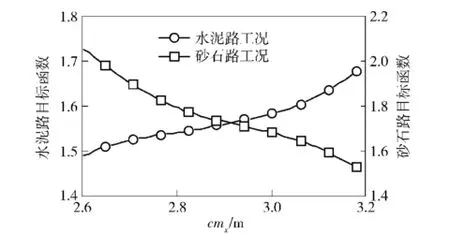
圖16　目標函數隨cmx的變化曲線Fig.16 Objective functions vs.cmx

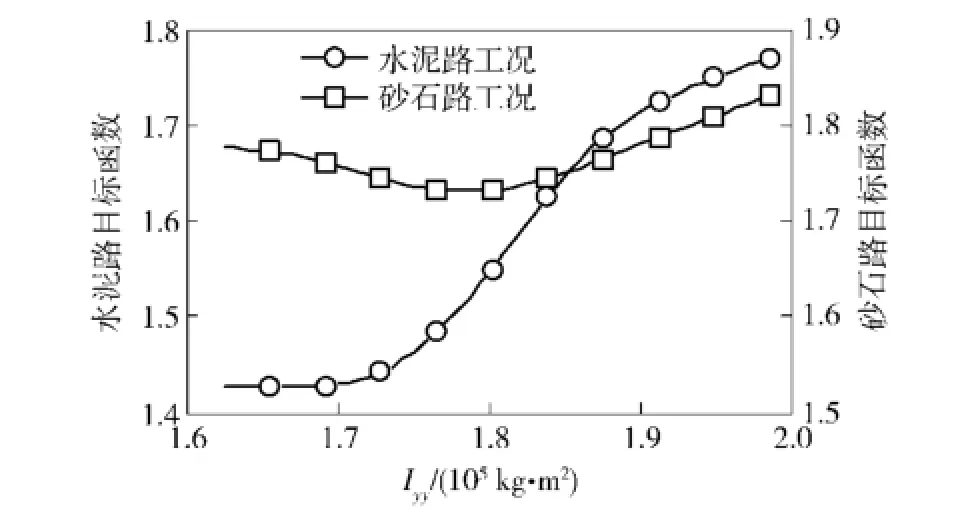
圖17　目標函數隨Iyy的變化曲線Fig.17 Objective functions vs.Iyy

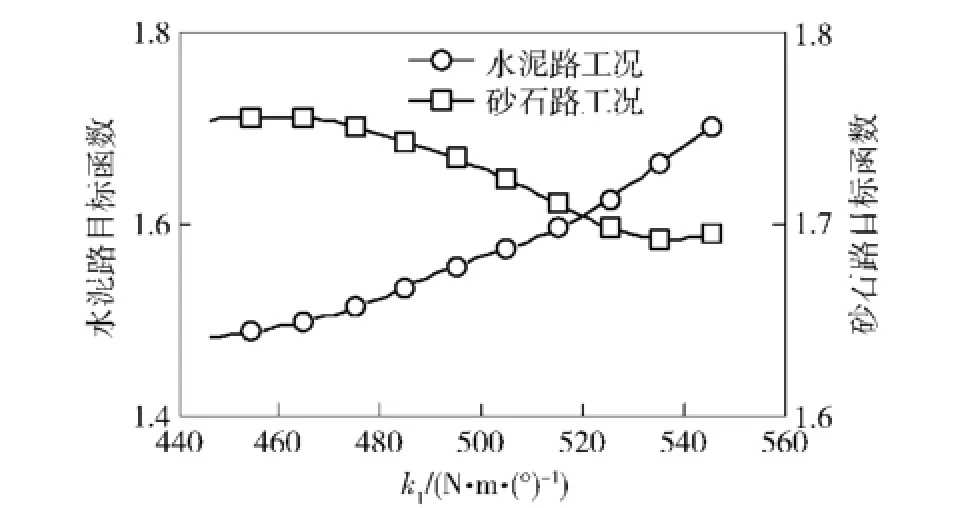
圖18　修正目標函數隨k1的變化曲線Fig.18 Objective functions vs.k1

由圖16～圖18可知，雖然水泥路和砂石路工況的目標函數與參數Iyy的變化規律基本一致，但是與參數cmx、k1的變化規律皆相反，說明兩種工況的目標函數存在著一定的沖突。若采用傳統的單目標優化算法分別對水泥路和砂石路工況的模型參數單獨修正，則不能同時取得最優解。因此，本文采用基于遺傳算法的多目標修正方法對水泥路和砂石路工況條件下的動力學模型參數同時進行修正。

5.2基于多目標遺傳算法的參數修正

動力學模型參數修正的數學表達式為

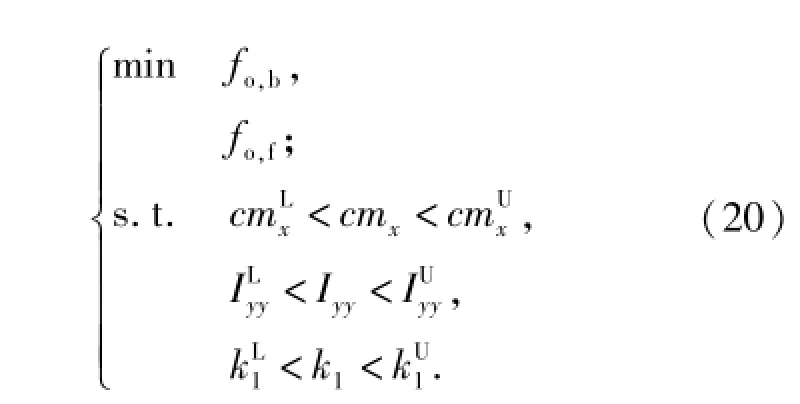
式中：fo，b和 fo，f分別為水泥路和砂石路工況下的修正目標函數；修正參數上標L、U分別表示參數取值下限和上限，與近似模型的參數設計區間一致。

目前，用于多目標優化問題的遺傳算法主要有：鄰域培植遺傳算法NCGA、存檔微遺傳算法NSGA、第一代非支配遺傳算法NSGA和第二代非支配遺傳算法NSGA-Ⅱ等。其中，NSGA-Ⅱ是一種帶精英策略的遺傳算法，其搜索尋優性能良好，在非支配排序中，接近Pareto前沿的個體被選擇，因而其Pareto前進能力強，收斂效率高，是目前求解多目標優化問題最有效的遺傳算法［13］。NSGA-Ⅱ的計算流程［14］如圖19所示。

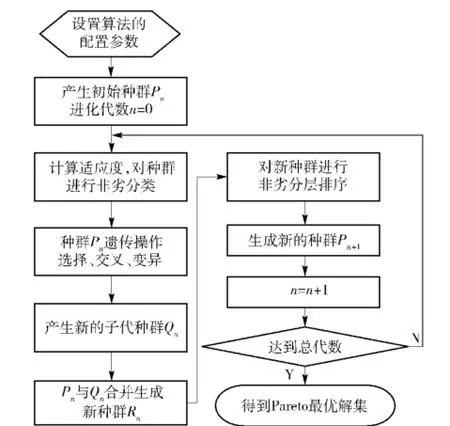
圖19　非支配遺傳算法NSGA-Ⅱ的計算流程Fig.19 Calculation flow of NSGA-Ⅱ

在本文的參數修正問題中，設置初始種群數為12，總進化代數20，共進行240次迭代計算，得到的參數修正Pareto前沿如圖20所示。

由圖20可知，NSGA-Ⅱ搜索得到的Pareto前沿大致呈一條光滑的曲線分布，前沿表面大多數Pareto最優解均可搜索到，且砂石路工況目標函數的尋優方向與水泥路工況目標函數的尋優方向相反，體現了參數修正問題中兩個目標函數與修正參數之間變化規律相互沖突的現象。表3為根據參數修正Pareto前沿得到的部分具有代表性的修正結果及其相對于參數修正前的目標函數變化率。

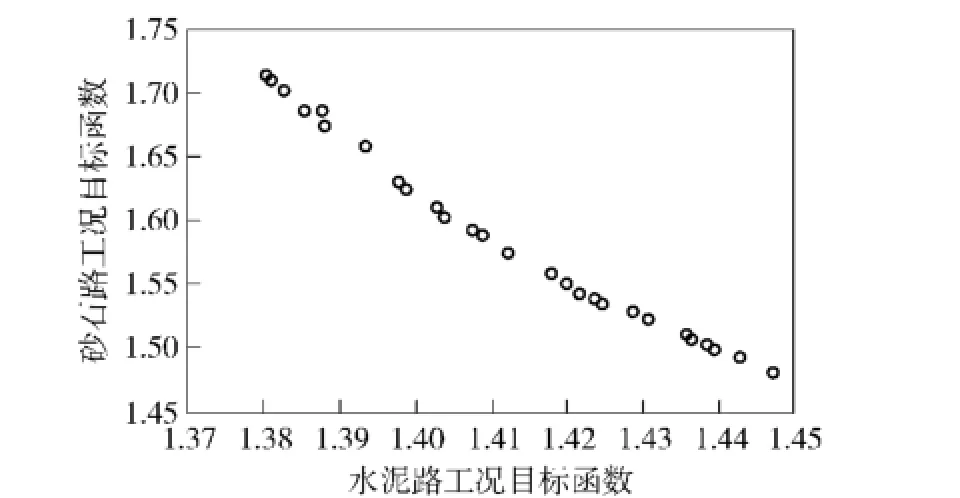
圖20　動力學模型參數修正的Pareto前沿Fig.20 Pareto front of dynamic model parameter updating

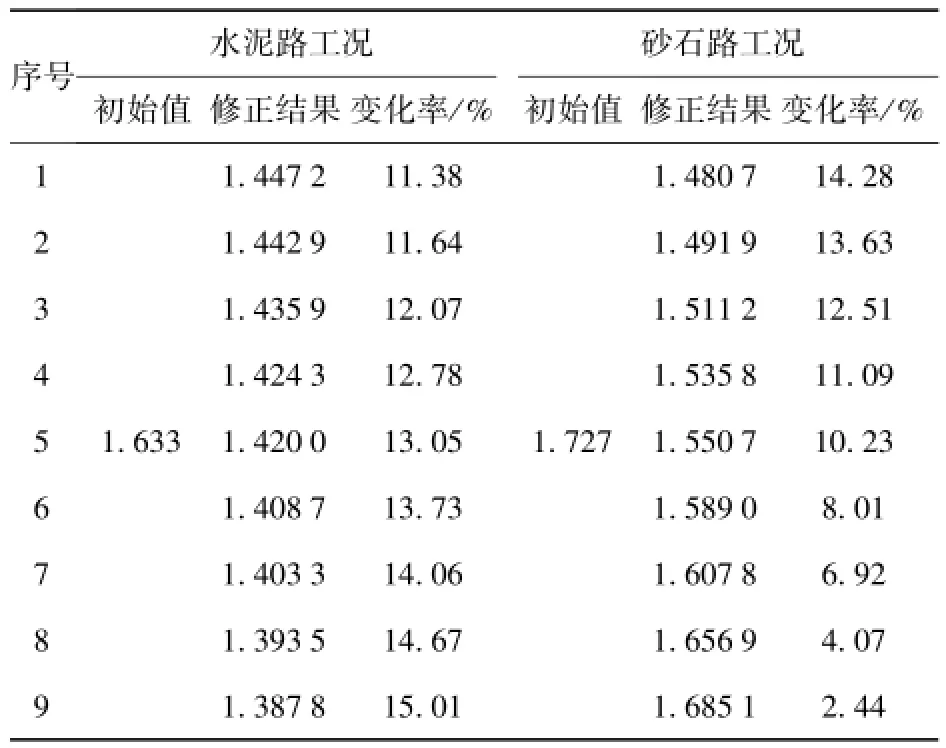
表3　模型修正結果及變化率Tab.3 Updated results and rate of change

由表3可知，在修正參數的設計區間內，水泥路和砂石路工況目標函數的變化率分別在11.38%～15.01%和2.44%～14.28%之間，雖然水泥路工況第9解的修正效果達到了最佳，但此時砂石路工況的修正效果不明顯，只有2.44%，此外，高速履帶車輛在實際行駛過程中，砂石路面行駛里程占總行駛里程的比例最高，對車輛動力學性能的影響最大，因此選擇砂石路工況條件下修正效果最佳的第1解作為參數修正的最終解。將第1解對應的修正參數代入高速履帶車輛多體動力學模型中，重新計算兩種工況的動力學響應，并與參數修正前的仿真結果和實車測試結果對比，如圖21和圖22所示。

由表3、圖21和圖22可知，與修正前相比，水泥路工況目標函數變化率為11.38%，砂石路工況目標函數變化率為14.28%，修正效果明顯，且修正后的功率譜密度曲線與實車測試結果更加接近，從功率譜密度曲線主峰值看，水泥路工況修正后的仿真值相對于試驗值的誤差由修正前的51.67%減小至13.50%，砂石路工況修正后的仿真值相對于試驗值的誤差由修正前的21.64%減小至9.88%，說明仿真結果的準確度得到了有效的提高，同時也證明了基于多目標遺傳算法的模型參數修正方法的有效性。

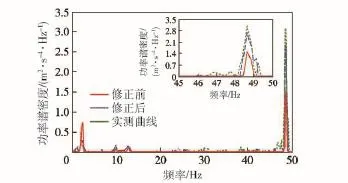
圖21　水泥路工況修正前后仿真結果與實測結果對比Fig.21 Comparison of test results and simulated results before and after parameter updating under the condition of cement road

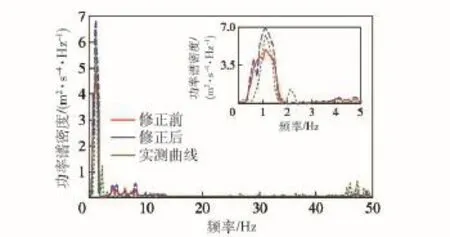
圖22　砂石路工況修正前后仿真結果與實測結果對比Fig.22 Comparison of test results and simulated results before and after parameter updating under the condition of gravel road

6　結論

本文以某型高速履帶車輛為研究對象，針對兩種典型隨機路面行駛工況，為提高動力學模型仿真結果的準確度，提出了基于多目標遺傳算法的模型修正方法，主要結論如下：

1）根據高速履帶車輛實車測試結果和動力學仿真結果的對比，初步驗證了動力學模型的可信性，并分析了兩種工況下車體振動響應的主要激勵源。

2）采用正交實驗設計對模型參數進行了篩選，該方法直觀簡單且計算量小，特別適于參數多，計算成本高的動力學模型參數修正問題。

3）根據修正參數隨修正目標函數的變化規律，對水泥路和砂石路工況條件下的動力學模型進行同時修正，采用第二代非支配遺傳算法NSGA-Ⅱ求解，得到了參數修正的Pareto前沿，并確定了最終解，結果表明：修正后模型仿真結果的準確度得到了明顯的提高，證明了基于多目標遺傳算法的模型修正方法的有效性。

參考文獻（References）

［1］ 韓寶坤，李曉雷，孫逢春.履帶車輛動力學仿真技術的發展與展望［J］.兵工學報，2003，24（2）：246-249. HAN Bao-kun，LI Xiao-lei，SUN Feng-chun.Present state and future outlook of the simulation of tracked vehicles［J］.Acta Armamentarii，2003，24（2）：246-249.（in Chinese）

［2］ Ferretti G，Girelli R.Modelling and simulation of an agricultural tracked vehicle［J］.Journal of Terramechanics，1999，36（3）：139-158.

［3］ Rubinstein D，Hitron R.A detailed multi-body model for dynamic simulation of off-road tracked vehicles［J］.Journal of Terramechanics，2004，41（2/3）：163-173.

［4］ 馬偉標，王紅巖，芮強.基于廣義簡約梯度算法的履帶車輛模型參數修正［J］.系統仿真學報，2012，24（4）：774-779. MA Wei-biao，WANG Hong-yan，RUI Qiang.Researchon model updating for tracked vehicle dynamic model based on generalized reduced gradient method［J］.Journal of System Simulation，2012，24（4）：774-779.（in Chinese）

［5］ 居乃鵕.裝甲車輛動力學分析與仿真［M］.北京：國防工業出版社，2002. JU Nai-jun.Dynamics analysis and simulation for armored vehicle ［M］.Beijing：National Defense Industry Press，2002.（in Chinese）

［6］ 丁法乾.履帶式裝甲車輛懸掛系統動力學［M］.北京：國防工業出版社，2004. DING Fa-qian.Dynamics of tracked armored vehicle suspension system［M］.Beijing：National Defense Industry Press，2004.（in Chinese）

［7］ 王欽龍，王紅巖，芮強.輪式越野車動力學建模及行駛動力學特性仿真分析［J］.裝甲兵工程學院學報，2012，26（5）：34-38. WANG Qin-long，WANG Hong-yan，RUI Qiang.Dynamic modeling and simulation analysis on ride dynamic of wheeled off-road vehicle［J］.Journal of Academy of Armored Force Engineering，2012，26（5）：34-38.（in Chinese）

［8］ 陳立平，張云清，任衛群，等.機械系統動力學分析及 ADAMS應用教程［M］.北京：清華大學出版社，2005. CHEN Li-ping，ZHANG Yun-qing，REN Wei-qun，et al.Dynamic analysis of mechanical system and application course of ADAMS ［M］.Beijing：Tsinghua University Press，2005.（in Chinese）

［9］ Mitschke M，Wallentowitz H.汽車動力學［M］.陳萌三，余強，譯.北京：清華大學出版社，2009. Mitschke M，Wallentowitz H.Dynamic of vehicle［M］.CHEN Meng-san，YU Qiang，translated.Beijing：Tsinghua University Press，2009.（in Chinese）

［10］ Bu D X，Sun W，Yu H S，et al.Adaptive robust control based on RBF neural networks for duct cleaning robot［J］.International Journal of Control Automation and Systems，2015，13（2）：475-487.

［11］ 高雋.人工神經網絡原理及仿真實例［M］.北京：機械工業出版社，2003. GAO Jun.Theory and simulation example of artificial neural network［M］.Beijing：China Machine Press，2003.（in Chinese）

［12］ David V，Sánchez A.Searching for a solution to the automatic RBF network design problem［J］.Neurocomputing，2002，42（1）：147-170.

［13］ 李偉平，王世東，周兵，等.基于響應面法和NSGA-Ⅱ算法的麥弗遜懸架優化［J］.湖南大學學報：自然科學版，2011，38（6）：28-32. LI Wei-ping，WANG Shi-dong，ZHOU Bing，et al.Macpherson suspension parameter optimization based on response surface method and NSGA-Ⅱalgorithm［J］.Journal of Hunan University：Natural Science，2011，38（6）：28-32.（in Chinese）

［14］ Chen S M，Shi T Z，Wang D F，et al.Multi-objective optimization of the vehicle ride comfort based on Kriging approximate model and NSGA-Ⅱ［J］.Journal of Mechanical Science and Technology，2015，29（3）：1007-1018.

中圖分類號：TJ811

文獻標志碼：A

文章編號：1000-1093（2016）06-0969-10

DOI：10.3969/j.issn.1000-1093.2016.06.002

收稿日期：2016-01-10

基金項目：軍隊“十二五”預先研究項目（2011YY18）

作者簡介：王欽龍（1987—），男，博士研究生。E-mail：wang_qinlong@126.com；王紅巖（1965—），男，教授，博士生導師。E-mail：why_cvt@263.net

Research on Parameter Updating of High Mobility Tracked Vehicle Dynamic Model Based on Multi-objective Genetic Algorithm

WANG Qin-long，WANG Hong-yan，RUI Qiang
（Department of Mechanical Engineering，Academy of Armored Forces Engineering，Beijing 100072，China）

Abstract：A method of model parameter updating is researched to improve the accuracy of simulation results of high mobility tracked vehicle dynamic model.A dynamic model of high mobility tracked vehicle is established，and the cement road and the gravel road are selected for updating the model parameters according to the statistical regularity of the driving conditions.The simulation results of dynamic model without parameter updating and the corresponding real vehicle test results under the same driving conditions are compared and analyzed，and the expression of objective function for model parameter updating is given.The updating parameters which influence objective function strongly are screened by using orthogonal experiment design method.The radial basis function neural network approximation models about the relation among updating parameters and objective functions are established to solve the issues of large calculation quantity and inefficiency of parameter updating.By analyzing the change rule of objective functions with updating parameters，the dynamic model parameters are updated simultaneously by using the second non-dominated sorting genetic algorithm（NSGA-Ⅱ）for two driving conditions.The final resultsof parameter updating are obtained.The research results show that the simulation accuracy of high mobility tracked vehicle dynamic model is effectively improved，and the availability of the proposed method is validated.

Key words：ordnance science and technology；high mobility tracked vehicle；parameter updating；multiobjective genetic algorithm；radial basis function neural network