雙旋靜穩定彈的共振不穩定研究

張衍儒 肖練剛 邱 奕 周 華

北京航天自動控制研究所，北京 100854

?

雙旋靜穩定彈的共振不穩定研究

張衍儒 肖練剛 邱 奕 周 華

北京航天自動控制研究所，北京 100854

由于雙旋彈的鴨舵和彈體相對旋轉，非對稱固定翼鴨舵方位角的改變干擾了雙旋彈角運動的周期，如果這個干擾的頻率與彈體自由擺動的頻率相同就會發生共振，共振的出現使攻角突增或發散，造成飛行不穩，這種不穩定稱為共振不穩定。本文分析了雙旋靜穩定彈角運動方程，討論了共振不穩定的特性。研究可知，攻角運動的振幅與固定翼鴨舵的轉速和雙圓運動的兩個頻率有關，固定翼鴨舵轉速的不合理可能引起攻角運動的發散，而保持固定翼鴨舵轉速遠離雙圓運動2個頻率可以有效避免雙旋彈的共振不穩定。

雙旋靜穩定彈；共振不穩定；固定翼鴨舵；雙圓運動

近年來，由于制導武器的低成本和小型化需要，雙旋靜穩定彈被作為一個主要的研發方向，進行了多次實彈研發。例如，MGK型120mm雙旋制導迫擊炮彈[1]、RCFC型81mm雙旋制導迫擊炮彈[2]、RCFC型120mm雙旋制導迫擊炮彈[2]和RCFC型掛飛制導炸彈[3]。

圖1 雙旋靜穩定彈的實彈示例

上述雙旋靜穩定彈的飛行穩定性可以通過彈體外形的靜穩定特性實現，但是攻角的變化規律與鴨舵轉速的對應關系缺少理論方面的介紹，本文探索并研究了攻角運動振幅與固定翼鴨舵轉速的對應關系，最終提出了有效避免雙旋彈共振不穩定[4]的控制方案。

1 雙旋靜穩定彈的控制原理

傳統基于十字鴨舵的6自由度控制方式，雖然可以精確實現橫法向過載修正，但是整體設計成本較高，為了降低成本，改裝鴨舵為固定翼鴨舵，固定翼鴨舵由2對固定舵角的舵片組成，其中1對舵片的偏轉方向相反，用于提供鴨舵反向旋轉所需的外部氣動導轉力矩，如圖2中滾轉舵片1和3；另一對舵片的偏轉方向相同，用于提供彈體姿態調整的氣動控制力矩矢量，如圖2中俯仰舵片2和4。

圖2 雙旋彈的繞質心運動

固定翼鴨舵通過內部的軸承繞彈體縱軸旋轉，當固定翼鴨舵的滾轉角速度為0時，固定翼鴨舵相對彈體縱軸靜止。此時固定翼鴨舵的俯仰舵片產生鴨舵氣動控制力，考慮繞質心運動，可以得到鴨舵氣動控制力矩。由于雙旋彈為靜穩定彈，因此彈體壓心在質心后，考慮彈體繞質心的動力學方程，可知彈體靜力矩和鴨舵氣動控制力矩能夠滿足力矩平衡條件，使雙旋彈產生相應的合成攻角。考慮全彈質心運動的動力學方程，可知彈體縱軸向鴨舵氣動力矢量方向移動，根據上述原理實現雙旋彈的制導飛行控制。

2 推導雙旋彈攻角運動方程

雙旋彈制導飛行時，主要有鴨舵旋轉和鴨舵靜止2個狀態，其中鴨舵旋轉狀態用于雙旋彈的導航姿態初始化[5]，與共振不穩定相關，鴨舵靜止狀態用于制導飛行控制，與靜穩定特性相關。

為了方便攻角運動方程推導，引入以下符號：

(1)

(2)

彈體縱軸相對理想彈道的高低角和方向角分別為φpc=φpg-θ和εpc=εpg，簡化繞質心運動的動力學方程為：

(3)

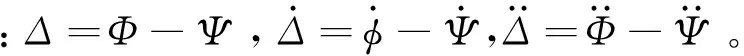
將式(2)寫為復數形式，忽略重力側向力(gsinθΨ=0)可得：

(4)

將式(3)寫為復數形式可得：

(5)

由式(4)求導數可得：

(6)

(7)

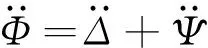
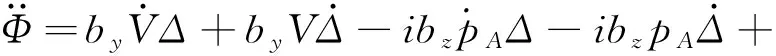
(8)

(9)

(10)

利用上述符號，簡化合成攻角Δ關于弧長s的表達式為：

(11)

3 固定翼鴨舵旋轉時攻角變化規律

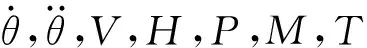
Δ=ΔPA+ΔPg+ΔPF

(12)

二圓角運動的齊次方程通解為：

ΔPA=C1eiω1s+C2eiω2s

(13)

式中：系數C1和C2由初始條件決定；ω1和ω2為齊次方程的特征根，也是雙圓運動的頻率，即彈體的自由擺動的頻率，忽略小量PT和T可得：

(14)

考慮由固定翼鴨舵引起的角運動，由式(11)可知角運動方程可寫為：

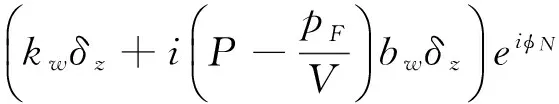
(15)

假設固定翼鴨舵轉速pF為常值，不考慮起始滾轉角所造成的差異，當pF(s)=pF/V而不等于齊次方程特征頻率ω1,2時，式(15)的非齊次特解可寫為如下形式：

ΔPF=KφNe-ipF(s)s

(16)

將式(16)帶入式(15)中，可解出：

(17)

略去數值較小的馬格努斯力矩項T和阻尼項H，同時注意到kwδz?(P-pF(s))bwδz，KφN可近似為：

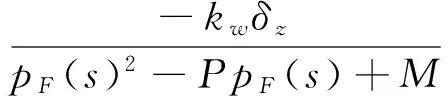
(18)

因此，當固定翼鴨舵以轉速pF勻速旋轉時，攻角受迫運動規律可近似為等幅周期運動，幅值大小為KφN，周期為pF(s)。

4 共振不穩定仿真試驗

仿真驗證攻角運動振幅與固定翼鴨舵轉速的對應關系，即式(18)是否正確。分別測試pF為-2π(°)/s，-π(°)/s時實際攻角T_alpha的幅值與通過式(18)計算得到的估計幅值KφN是否一致，仿真結果如圖3所示。

圖3 攻角估計值K與實際攻角T_alpha幅值的對比曲線

由圖3可知，實際攻角T_alpha幅值變化規律與理論值吻合較好，合成攻角的幅值可以通過式(18)求取的估計值K近似得到。

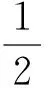
圖4 雙旋靜穩定彈的攻角雙圓運動

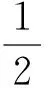
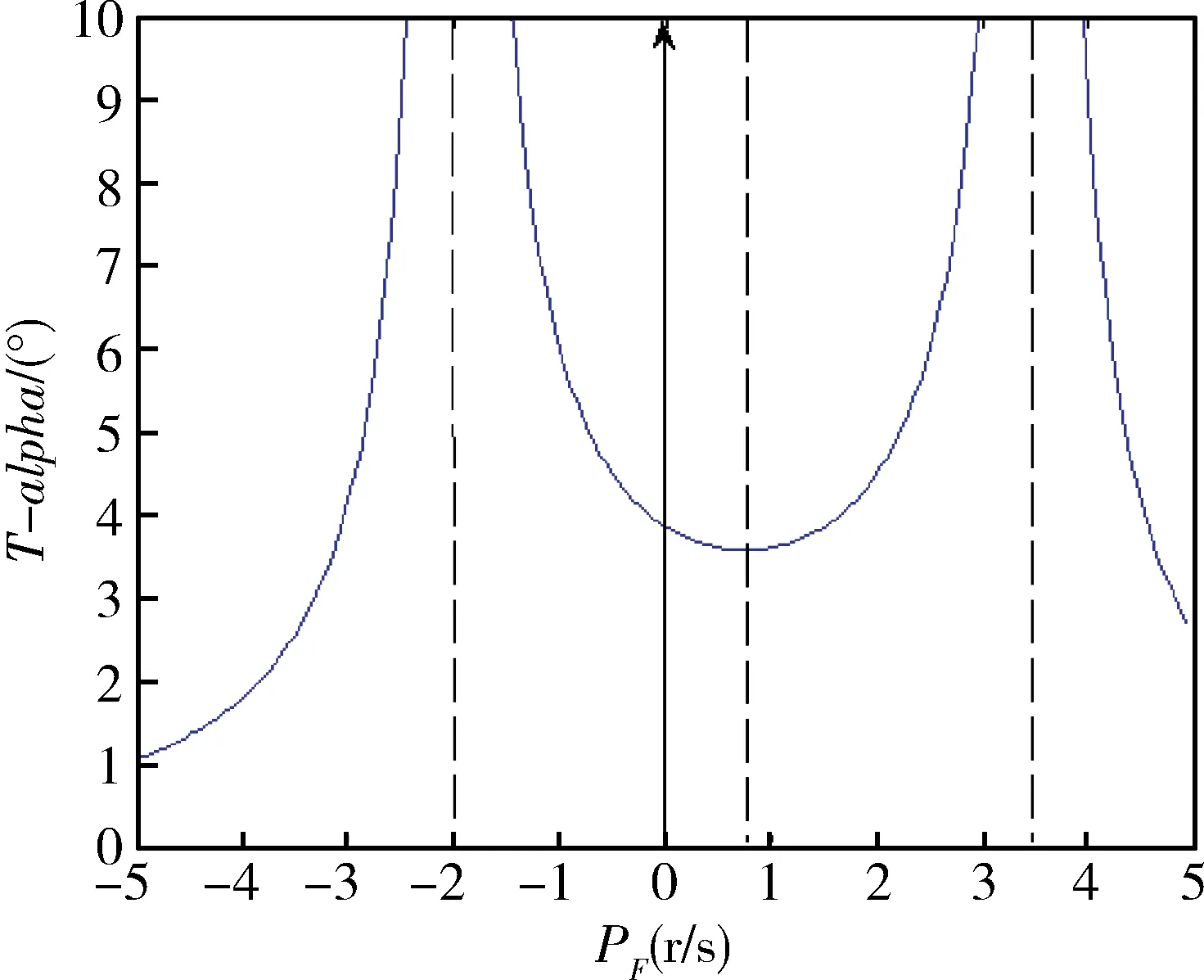
圖5 實際攻角T_alpha幅值隨固定翼鴨舵轉速變化趨勢

由圖5可知，合成攻角T_alpha的幅值會在pF(s)與ω1,2趨于一致時不斷增大，呈現出發散的趨勢，從而產生共振不穩定。

通過上述分析可知，可以調節固定翼鴨舵的滾轉角速度pF實現合成攻角T_alpha的幅值變化，該項技術可用于固定翼鴨舵的姿態初始化過程中。需要注意的是，固定翼鴨舵消旋進入X軸陀螺儀量程范圍的過程中，應該快速通過雙旋彈的共振頻率，避免引起雙旋彈的共振不穩定，如圖6所示。

圖6 有效避免雙旋彈共振不穩定的過程

由圖6可知，固定翼鴨舵轉速通過共振不穩定轉速頻率時，攻角會有一個增大的過程，固定翼鴨舵的滾轉控制算法應使鴨舵轉速快速通過共振區域，從而有效避免雙旋彈的共振不穩定。

5 結論

通過雙旋靜穩定角運動方程研究固定翼鴨舵制導炮彈的共振不穩定性，通過數學推導與仿真分析，得出固定翼鴨舵的轉速及雙圓運動頻率影響攻角運動，其中，固定翼鴨舵轉速是關鍵，設計時使其遠離雙圓頻率可以避免共振不穩定性。

[1] Kelly Hanink. Mortar Guidance Kit (MGK) [R]. America: 2010 Joint ArMaments Conference, 2010.

[2] Yousef Habash. Roll Control Guided Mortar (RCGM) [R].America: NDIA Joint ArMaments Conference, 2012.

[3] Asad Khan. Project Overview-Precision Air Dropped Guided Munition(PADGM) [C]. America: 46th Annual Gun & Missile Systems Conference & Exhibition, 2011.

[4] 韓子鵬. 彈箭外彈道學[M].北京: 北京理工大學出版社，2008：261-273.(Han Zipeng. Rocket Exterior ballistics [M].Beijing Institute of Technology press, 2008:261-273.)

[5] 張衍儒, 肖練剛. 旋轉控制固定鴨舵的導航初始化與控制算法研究[J].航天控制, 2014, 32(6):35-39.(Zhang Yanru, Xiao liangang. Navigaion Initialization and Control Algorithm of Roll Control Fixed Canards[J]. Aerospace Control, 2014, 32(6):35-39.)

Research on Resonance Instability of Dual-Spin Static Stability Projectile

Zhang Yanru, Xiao Liangang, Qiu Yi, Zhou Hua

Beijing Aerospace Automatic Control Institute, Beijing 100854，China

Duetotherelativerotationbetweenthecanardsandthebodyofthedual-spinprojectile,theangularperiodicdisturbanceofthedual-spinmotionisformedbytherotationoffixedcanards.Ifthefrequencyisthesameasthebodyvibrationfrequency,theresonanceoccursandthentheangleofattackisincreasedbyresonancewhichresultsinflightinstability,therefore,thisinstabilityiscalledresonanceinstability.Inthispaper,thecharacteristicsofresonantinstabilityareresearchedbyanalyzingtheangularmotionequationofdual-spinstaticstabilityprojectile.Astheresearchreveals,theamplitudeoftheangleofattackisrelatedtothespeedofthefixedcanardsandthetwofrequenciesoftwo-circlemovementandthedivergenceoftheattackangleiscausedbytheunreasonablespinspeedoffixedcanards,andwhenthespinspeedofthefixedcanardsisfarfromthetwofrequenciesoftwocircularmotion,theresonanceinstabilitycanbeavoidedeffectively.

Dual-spinstaticstabilityprojectile;Resonantinstability;Fixedcanards;Twocirclemovement

2015-09-21

張衍儒(1985-)，男，哈爾濱人，博士，工程師，主要研究方向為制導彈藥控制系統綜合；肖練剛(1973-)，男， 四川資中人，博士，研究員，主要研究方向為導航、制導與控制；邱 奕(1990-)，男，四川重慶人，碩士，助理工程師，主要研究方向為導航、制導與控制；周 華(1989-)，男，湖南衡陽，碩士，助理工程師，主要研究方向為導航、制導與控制。

TJ412.+1

A

1006-3242(2016)03-0031-05