改進的多數據流協同頻繁項集挖掘算法

王鑫 劉方愛

摘要：針對已有的多數據流協同頻繁項集挖掘算法存在內存占用率高以及發現頻繁項集效率低的問題，提出了改進的多數據流協同頻繁項集挖掘（MCMDStream）算法。首先，該算法利用單遍掃描數據庫的字節序列滑動窗口挖掘算法發現數據流中的潛在頻繁項集和頻繁項集；其次，構建類似頻繁模式樹（FPTree）的壓縮頻繁模式樹（CPTree）存儲已發現的潛在頻繁項集和頻繁項集，同時更新CPTree樹中每個節點生成的對數傾斜時間表中的頻繁項計數；最后，通過匯總分析得出在多條數據流中多次出現的且有價值的頻繁項集，即協同頻繁項集。相比AStream和HStream算法，MCMDStream算法不僅能夠提高多數據流中協同頻繁項集挖掘的效率，并且還降低了內存空間的使用率。實驗結果表明MCMDStream算法能夠有效地應用于多數據流的協同頻繁項集挖掘。

關鍵詞：

流數據挖掘；多數據流；滑動窗口；頻繁項集；協同頻繁項集

中圖分類號： TP301.6 文獻標志碼：A

0引言

隨著萬維網技術的迅速發展，復雜多樣的數據呈現爆炸式增長。數據流作為一種特殊形態的數據已在眾多領域中廣泛地應用，例如網絡實時監控的數據[1]、傳感器采集的數據[2]和金融市場的證券交易信息等。相對于傳統靜態數據而言，流數據具有實時、連續、大量、不確定和隨時間變化的特點，因此，在不斷變化的流數據上進行頻繁項集挖掘更具有挑戰性。

近年來，流數據頻繁項集挖掘[3]成為研究的熱點問題。1998年，Henzinger等[4]首次將流數據作為一種數據模型提出來。根據處理數據流時所采用的時序范圍，將數據流模型劃分為3個范疇：界標模型、快照模型和滑動窗口模型。以界標模型為基礎，Manku等[5]提出了一種近似數據流頻繁項集挖掘（Lossy Counting）算法，該算法能夠有損耗地計算整個數據流中元素出現的近似頻率，但因其效率不高、動態性不強；Yu等[6]提出了以假消極結果為導向在有限內存中挖掘數據流中頻繁項集的流數據頻繁模式挖掘（Frequent Data Stream Pattern Mining， FDPM）算法，但是Lossy Counting和FDPM算法只能得到近似的結果，因此，從流數據中獲得當前準確頻繁項集的科研成果隨之涌現。Mozafari等[7]將滑動窗口引入數據流的傳送中，并提出了一種新的技術概念Vertification，以此為基礎設計了根據滑動窗口的大小調節性能和擴展性的滑動窗口增量挖掘（Sliding Window Incremental Miner， SWIM）算法。Leung等[8]構造了一種能夠精確地挖掘數據流中頻繁項集的新型樹形索引結構（Data Stream Tree，請補充DSTree的英文全稱。 DSTree）。以上算法只針對單數據流頻繁項集的挖掘，但是結合當前的諸多應用，需要解決在多數據流環境[9-10]中頻繁項集挖掘的問題，因此，Guo等[11]提出了HStream算法，目的是發現多數據流中的頻繁項集問題。該算法以FPGrowth算法[12]為基礎挖掘單條數據流中的頻繁項集并將其頻數存儲于節點的自然傾斜時間窗口表中，通過匯總挖掘在多條數據流中多次出現的頻繁項集。在此過程中需要多遍掃描數據庫以及生成大量不必要的單位時間窗口，從而導致發現頻繁項集時既耗時又浪費內存占用空間。

針對上述HStream算法低效、內存利用率不高的問題，本文提出了一種基于滑動窗口的多數據流協同頻繁項集挖掘（Mining Collaborative Frequent Itemsets in Multiple Data Stream， MCMDStream）算法。該算法首先通過基于字節序列的滑動窗口挖掘（Ming Frequent Itemsets within a TimeInterval Sliding Window based on based on bitsequence， TISWMFI）算法發現數據流中的潛在頻繁項集和頻繁項集；然后構建CPTree用來存儲多數據流中的頻繁項集和潛在頻繁項集，同時更新樹節點中對數傾斜時間表中項集對應的頻數；最后匯總分析得出多數據流中的協同頻繁項集。與HStream算法中HTree的自然傾斜時間窗口表相比，MCMDStream算法中新引入的對數傾斜時間窗口表能夠增量更新CPTree；同時還能夠大量地減少節點總數，從而降低了算法的維護代價與空間復雜度；本文新引入的TISWMFI算法相比HStream中的FPGrowth而言，能夠減少對數據庫的遍歷次數以及查詢時間，因此，MCMDStream算法具有更強的適應性和擴展性。

1相關描述與問題定義

設S={S1，S2，…，Sn}為一組數據流集合，其中：Si表示一組大量的連續到達的流數據d1j，d2j，…，dij的數據序列，dij（i≥1，1≤j≤n）表示在第i時刻第j條數據流的值。

定義1項集I[5]。令I={i1，i2，…，im}為所有項的非空集合，其中m為項集的長度，包含k個項的項集稱為k項集。例如項集{a，b}為2項集。

定義2事務數據流T[5]。表示一個連續的事務序列，即T=T1，T2，…，Tn，且TI。設Tid為事務數據流Ti的唯一標識符，TUid為時間單位標識符，事務T={TUid，Tid，Itemset}。

定義3滑動窗口SW[4]。指在單位時間內進行滑動的一個獨立窗口，其中單位時刻TUi包含一個變量，即SW=[TUn-w+1，TUn-w+2，…，TUn]。其中：n-w+1表示當前滑動窗口單位時間標識號；w表示SW的總長度，且w=TUn-w+1+TUn-w+2+…+TUn。

定義4頻繁項集（Frequent Itemset， FI）[4]。設項集X在滑動窗口SW中的支持度為Sup（X）SW，若Sup（X）SW≥θ·w，則稱X為一個頻繁項集（FI）。其中，θ（θ∈[0，1]）表示用戶自定義的最小支持度閾值。

定義5協同頻繁項集（Collaborative Frequent ItemsetCFI的英文全稱補充得是否正確？請明確。， CFI）。設在給定數據流Si中的項集O，若tOSimax-tOSimin≤θ（tOSimax=max{t1，t2，…，tk}，tOSimin=min{t1，t2，…，tk}），則O是一個協同項集（Collaborative Itemset， CI）。若協同項集CI在隨后給定的時間里以同樣的方式在數據流集合Φ的數據流Si中頻繁出現，則稱CI為一個協同頻繁項集。

定義6最大誤差因子ε。令ε在系統允許范圍內控制算法精度。若ε≤Sup（X）SW≤θ，則項集X為潛在頻繁項集（Potential Frequent Itemset， PFI）；若Sup（X）SW≤ε，則項集X為非頻繁項集（UnFrequent Itemset請補充PFI、UFI的英文全稱。， UFI）。PFI、UFI都是針對特定時間段定義的。例如，在時間段t1內，項集X為FI；而在t2內，X可能為PFI或UFI。

2算法描述

在本文中，將多數據流協同頻繁項集挖掘分為3步：

第1步利用新引入的TISWMFI算法從數據流中產生一組潛在頻繁項集以及頻繁項集；

第2步構建一棵基于字典序列的前綴樹CPTree用來保存數據流中頻繁項集動態的變化趨勢，在此重新設計了CPTree結構，加入了對數傾斜時間窗口記錄FI的頻繁數；

第3步利用MCMDStream算法從潛在頻繁項集中發現協同頻繁項集。

2.1CPTree結構

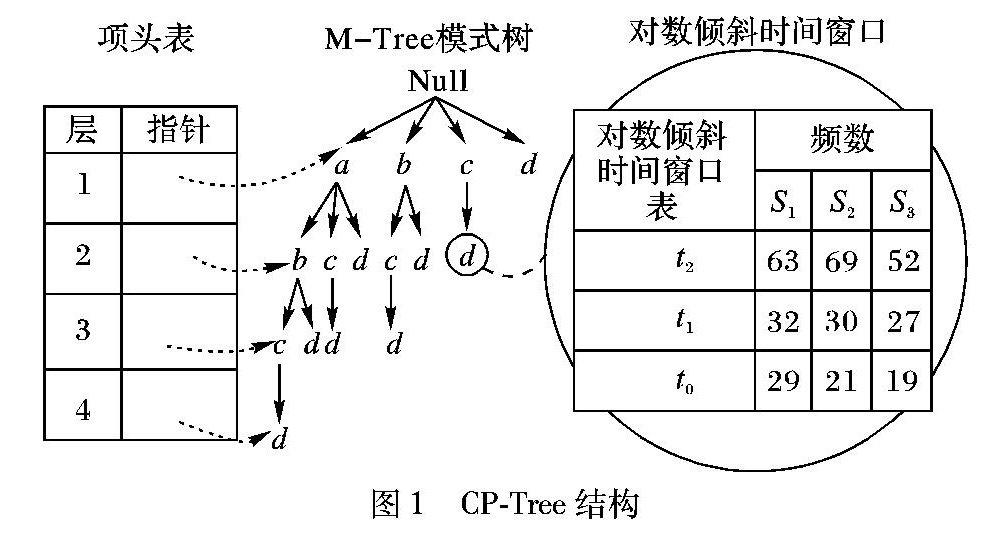
結構上，CPTree由MTree、Header Table和Logarithmic Tilted Window三部分組成，該結構如圖1所示。

1）MTree。記錄頻繁項集動態變化的一棵字典序列前綴樹，用來存儲數據流中頻繁的和潛在頻繁的項集。

2）Header Table。一個指向MTree中不同層中節點指針的數組。利用Header Table，能夠高效地從MTree中挖掘出頻繁的和潛在頻繁的項集，減少更新樹中頻繁項集的時間，從而提高遍歷樹結構的效率。

3）Logarithmic Tilted Window。為了進一步地降低內存占用率以及算法的空間復雜度，新增加了對數傾斜時間窗口LW。滑動窗口SW由大小固定且連續的LW序列組成，記為{LW1，LW2，…，LWm}。在每個時間間隔內，LW為每個節點都創建了相對應的時間窗口表保留頻繁項集的計數值。在n組數據流中，每個頻繁項所需操作的數是對整個數據流數據進行操作的總數再除以N。

2.2TISWMFI算法

針對在有限的物理存儲空間挖掘頻繁項集會多次掃描數據庫的問題，本文提出了一種新穎的單程掃描算法，即基于字節序列的滑動窗口挖掘（Ming Frequent Itemsets within a TimeInterval Sliding Window based on sequence of bytes， TISWMFI）算法，目的是挖掘給定時間t中SW內數據流Si的頻繁項集。TISWMFI將SW內所有的數據項都以字節序列的形式表示，保證所有的項只被掃描一次，因此，該算法不僅能夠提高內存利用率，而且還提高了動態存儲事務的速度。

2.2.1字節序列表示法

字節序列表示法是指用二進制位（0或1）表示在SW內數據流Si的事務Ti中項X的支持度計數Sup（X）和出現的頻數fx，項X的字節序列表示為Bit（X）。設在當前SW中項X存在于Ti中，則項X的第i位記為1，即Bit（X）=1；否則記為0，即Bit（X）=0。隨著窗口的不斷滑動，需要維護項的字節序列，因此，在計算Sup（X）時，2個k項集的字節序列進行“按位與”操作，便得到（k+1）項集（k≥0）的字節序列；而在進行刪除操作時只需將原有的字節序列按位左移一位。該方法能夠使窗口快速地滑動而且還能用較小的存儲空間保存所有項集出現的情況。

在滑動窗口SW1和SW2中的事務數據流的項集字節序列為例。在表1中，SW1由〈T1，（abc）〉、〈T2，（bce）〉和〈T3，（abce）〉三條事務組成，并且項a在SW1的T1和T3中存在，因此Bit（a）=101、Bit（b）=111、Bit（c）=111、Bit（d）=000和Bit（e）=011。

2.2.2TISWMFI算法描述

TISWMFI算法由窗口初始化、窗口滑動和頻繁項集生成3個階段組成。具體過程如下。

步驟1滑動窗口初始化階段。當SW=Null時，將單位時間TUi內事務Ti中所有項按照字節序列表示法將其轉變為相對應的字節序列，直到SW=Full時結束。

步驟2窗口滑動階段。在步驟1的基礎上，將項X的字節序列“按位左移”即可將當前SW中失效事務中的項集移除。若Sup（X）SW=0，則可刪除項X。

步驟3頻繁項集產生階段。即已知的頻繁（K-1）項集以逐層迭代的方式構成候選K項集，并將相應的字節序列作“按位與”操作計算頻繁項集的支持度，即Bit（X）中字節1的總數。主要子步驟如下：

1）單遍掃描數據流Si，計算每個項的支持度，刪除支持度小于θ的項，構成頻繁1項集FI1；

2）將兩個FI1以自連接的方式構成包含候選2項集，保留支持度大于θ的項，形成頻繁2項集FI2；

3）以此類推，逐層迭代，直到沒有新的頻繁項集產生為止。

滑動窗口SW1和SW2四條事務數據流中的頻繁項集如表2所示，SW2由事務T2、T3和T4組成，現以SW2中頻繁項集生成過程為例。設θ=0.6，w=3，Sup（X）SW2=0.6×3=1.8。由此可得，Sup（b）=111、Sup（b）=3>1.8，Bit（c）=110、Sup（c）=2>1.8和Bit（e）=110、Sup（e）=2>1.8，即（b）、（c）和（e）構成FI1；利用FI1執行“按位與”操作，得到FI2，Bit（bc）=Bit（b） & Bit（c）=110、Sup（bc）=2，同理，Sup（be）=2、Sup（ce）=2；利用FI2執行“按位與”操作，得到FI3，Bit（bce）=Bit（bc） & Bit（be） & Bit（ce），Sup（bce）=2>1.8，因此，FI3為（bce）。

2.3MCMDStream算法

MCMDStream算法將TISWMFI算法中發現的頻繁項集保存在CPTree中，由θ控制FI的數量，ε控制CPTree剪枝率；其次，通過插入新的FI、PFI和刪除UFI持續更新CPTree；最后，深度優先遍歷CPTree發現多條數據流中的協同頻繁項集。假設n條數據流Si的集合Φ以批處理的方式挖掘，其中在時間間隔ti（i≥1）產生的第j（1≤j≤n）條數據流被標記為dij，遍歷自定義數據結構中的頻繁項集。多數據流協同頻繁項集挖掘算法偽代碼如下。

有序號的程序——————————Shift+Alt+Y

程序前

輸入：用戶自定義的最小支持度閾值θ；n條數據流集合S；最大誤差率ε；協同頻繁項集集合α。

輸出：協同頻繁項集。

//步驟1：Construct CPTree

1）

FI=Null， PFI=Null， i=1；

2）

for j=1 to n do

3）

FI= FI∪TISWMFI（dij，θ）；

PFI=CI∪TISWMFI（dij，θ，ε）；

4）

end for

5）

MTree=Initialize_MTree（FI，PFI）

//步驟2：Update CPTree

6）

While S≠Null do

7）

I=Null，i=i+1；

8）

Ci1，Ci2，…，Cin=Preprocessing（di1，di2，…，din，MTree，θ，ε）

9）

for j=1 to n do

10）

I=I∪TISWMFI（Cij）；

11）

end for

12）

MTree=Insert_CPTree（I），MTree=Prune_CPTree（MTree，θ，ε）；

13）

end while

//步驟3：Mining collaborative Frequent Itemsets across //Multiple Streams（在多數據流中挖掘協同頻繁項集）

14）

CFI=Collaboration_Mining（α）

15）

Output CFI

程序后

具體算法步驟如下。

步驟1利用TISWMFI算法從第一批數據流dij中提取FI和PFI。

步驟2構造CPTree，并初始化CPTree的MTree、Header Table和Logarithmic Tilted Window。計算各項集在指定時間窗口內的平均頻數并降序排列。將所有數據項E∈{FI∪PFI}插入到MTree中；同時將所有數據流中數據項E的頻繁項計數寫入每個節點相對應的對數時間窗口表中。根據頻繁計數對數據項E分類，同時，在Header Table增加一個指針指向MTree每一層首節點。

步驟3利用最新的數據流更新MTree。該過程有如下4個子步驟：

1）預處理最新的數據流，刪除dij中的UFI。

2）查找項集I，在每一條被預處理的數據流中查找未被剪枝的項集。

3）將數據項集I插入MTree中，若I已插入樹中，則僅更新窗口表中相對應數據項的計數值；否則，將在MTree插入I，同時更新CPTree的三部分。

4）調用末端剪枝函數Prune_CPTree（）刪除窗口末端的UFI。

步驟4當所有的數據流更新完成后，深度優先遍歷MTree，在多數據流集合Φ中挖掘協同頻繁項集CFI。

2.4算法性能分析

3實驗結果與分析

實驗環境配置為：Windows 7 Professional操作系統，Intel Core CPU i33220 @2.93GHz，1TB RAM。使用Microsoft Visual C++ Version 6.0實現算法以及數據流模擬生成模塊。模擬實驗主要從存儲代價、算法響應時間、查準率和查全率4個方面分別對AStream、HStream和MCMDStream算法進行對比分析。其中AStream算法是基于Aprior算法的挖掘頻繁項集的算法，通過對數據流進行多次掃描、自底向上的寬度優先搜索得到協同頻繁項集的一種算法。測試數據集是由IBM Quest MarketBasket合成數據生成器產生的6條數據流。每條數據流中包含2000個事務，其中：TLen表示每個事務的平均長度，NItems表示每個事務中每個項集的平均長度，如表3所示。

3.1存儲代價

內存使用量影響著算法的可擴展性，將MCMDStream與另外兩個多數據流頻繁項集挖掘算法AStream和HStream進行對比。假定在已處理的數據規模不變的情況下，測試IBM合成6條數據流分批到達構建CPTree樹結構時所產生的節點的總數。在最小支持度閾值和最大誤差率不變的前提下，分批處理事務數據流長度為5～30，步長為5。當所有的數據項插入CPTree后，各算法生成樹節點的總數如圖2所示。

從圖2可得，MCMDStream算法中樹結構生成的節點數量與AStream和HStream相比最少，因此所占用的內存空間最小，算法的存儲空間最低，即MCMDStream算法的空間復雜度較小。這是因為AStream算法僅用ε控制樹的剪枝率，因此包含了大量的潛在頻繁項集，HStream使用θ與ε同時控制剪枝率，而MCMDStream算法在使用θ與ε控制CPTree剪枝率的基礎上采用對數傾斜時間窗口，減少了每個節點中時間窗口的數量，便于冗余剪枝。最終減小了樹結構的內存使用率，從而降低了存儲代價。

3.2算法響應時間

該算法根據不同的支持度閾值產生不同的響應時間。測試各算法在IBM合成的6條數據流的響應時間。設在IBM數據集的支持度閾值變化范圍為1～5，步長為1。實驗結果分別如圖3所示。

從圖3中得出，HStream算法具有較高的事務敏感性。當事務數據量逐漸增大時，該算法因受剪枝策略的影響會產生較冗余的分支。HStream算法是在FPGrowth算法的基礎上進行頻繁項集挖掘，不僅需要掃描兩遍數據庫，而且還會產生大量的候選頻繁項集，因此在進行挖掘過程中消耗大量的時間。MCMDStream算法是基于字節序列的滑動窗口的頻繁項集挖掘，其在查詢過程中，只需建立一棵頻繁模式樹且只掃描一遍數據庫，因此節省了查詢響應時間，從而降低了MCMDStream算法的時間復雜度，查詢效率高于HStream和AStream。

3.3查準率和查全率

最大誤差值ε是算法中一項重要的剪枝參數，查準率是指算法發現的實際協同頻繁項集數與算法發現輸出數量的百分比，而查全率則為算法發現的實際協同頻繁項集數與真實數量的百分比。挖掘數據集的協同頻繁項集以最大誤差值ε作為剪枝參數，在更新樹結構時能夠影響算法的查準、查全率。圖4～5分別評估了在IBM合成的6條數據流中不同誤差值對算法查準、查全率的影響。假定誤差值ε分別為0.0002，0.0008，0.0014和0.002時IBM合成數據流中S1、S2和S3三條數據流的查準率和查全率。

從圖4和圖5中可以看出，對于不同的誤差值，MCMDStream算法的查準率和查全率高于其他算法。當誤差值增大時，頻繁項集的數量減少，因此用戶指定的誤差值越大，頻繁項集數量越少，挖掘多條數據流中的協同頻繁項集時的準確率和查全率就會越高。

4結語

本文提出了一種能夠高效地挖掘多數據流協同頻繁項集的MCMDStream算法。該算法不僅能夠減小內存利用率、縮短挖掘的查詢響應時間，而且還可以提高算法的查準率和查全率。模擬實驗利用IBM合成數據集驗證了該算法的性能優于AStream和HStream算法，能夠很好地應用于多數據流協同頻繁項集的挖掘，但是本文只考慮了單機上的多數據流頻繁項集挖掘問題，在今后的研究中，將采用分布式集群這一有效的途徑，實現大規模多數據流中協同頻繁項集發現問題。

參考文獻：

[1]

BHATTACHARYA S， MOON S. Network performance monitoring and measurement： techniques and experience [M]// Universal Access in HumanComputer Interaction. Access to Interaction. Berlin： Springer， 2015： 528-537.

[2]

王爽，王國仁.面向不確定感知數據的頻繁項查詢算法[J].計算機學報，2013，36（3）：571-581.（WANG S， WANG G R. Frequent items query algorithm for uncertain sensing data [J]. Chinese Journal of Computers， 2013， 36（3）： 571-581.）

[3]

金澈清，錢衛寧，周傲英.流數據分析與管理綜述[J].軟件學報，2004，15（8）：1172-1181.（JIN C Q， QIAN W N， ZHOU A Y. Analysis and management of streaming data [J]. Journal of Software， 2004， 15（8）： 1172-1181.

[4]

HENZINGER M R， RAGHAVAN P， RAJAGOPALAN S. Computing on data streams [C]// Proceedings of the 1999 External Memory Algorithms： DIMACS Workshop External Memory and Visualization. Boston： American Mathematical Society， 1999： 107-118.

[5]

MANKU G， MOTWANI R. Approximate frequency counts over data streams [C]// Proceedings of the 28th International Conference on Very Large Data Bases. [S.l.]： VLDB Endowment， 2002： 346-357.

[6]

YU J， CHONG Z， LU H， et al. False positive or false negative： mining frequent itemsets from high speed transactional data streams [C]// Proceedings of the Thirtieth International Conference on Very Large Data Bases. [S.l.]： VLDB Endowment， 2004： 204-215.

[7]

MOZAFARI B， THANKKAR H， ZANIOLO C. Verifying and mining frequent patterns from large windows over data streams [C]// ICDE 2008： Proceedings of the IEEE 24th International Conference on Data Engineering. Piscataway， NJ： IEEE， 2008： 179-188.

[8]

LEUNG C K S， KHAN Q. DSTree： a tree structure for the mining of frequent sets from data streams [C]// ICDM06： Proceedings of the 2006 Sixth International Conference on Data Mining. Piscataway， NJ： IEEE， 2006： 928-932.

[9]

HRISTIDIS V， VALDIVIA O， VLACHOS M， et al. Information discovery across multiple streams [J]. Information Sciences， 2009， 179（19）： 3268-3285.

[10]

YEH M Y， DAI B R， CHEN M S. Clustering over multiple evolving streams by events and correlations [J]. IEEE Transactions on Knowledge and Data Engineering， 2007， 19（10）： 1349-1362.

[11]

GUO J， ZHANG P， TAN J， et al. Mining frequent patterns across multiple data streams [C]// Proceedings of the 20th ACM International Conference on Information and Knowledge Management. New York： ACM， 2011： 2325-2328.

[12]

HAN J， PEI J， YIN Y， et al. Mining frequent patterns without candidate generation： a frequentpattern tree approach [J]. Data Mining and Knowledge Discovery， 2004， 8（1）： 53-87.

[13]

CHANG J H， LEE W S. Finding recent frequent itemsets adaptively over online data streams [C]// Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2003： 487-492.

[14]

AGRAWAL R， SRIKANT R. Privacypreserving data mining [C]// Proceedings of the 2009 ACM SIGMOD Record. New York： ACM， 2000， 29（2）： 439-450.

[15]

BERNECKER T， CHENG R， CHEUNG D W， et al. Modelbased probabilistic frequent itemset mining [J]. Knowledge and Information Systems， 2013， 37（1）： 181-217.