噴氣織機(jī)打緯機(jī)構(gòu)及墻板的振動(dòng)特性

金玉珍， 胡小冬， 林培峰， 胡旭東

(浙江理工大學(xué) 機(jī)械與自動(dòng)控制學(xué)院， 浙江 杭州 310018)

噴氣織機(jī)打緯機(jī)構(gòu)及墻板的振動(dòng)特性

金玉珍， 胡小冬， 林培峰， 胡旭東

(浙江理工大學(xué) 機(jī)械與自動(dòng)控制學(xué)院， 浙江 杭州 310018)

針對(duì)噴氣織機(jī)四連桿打緯機(jī)構(gòu)隨著轉(zhuǎn)速的不斷提高會(huì)引起的強(qiáng)烈振動(dòng)和噪音問(wèn)題，采用理論分析、數(shù)值模擬和實(shí)驗(yàn)相結(jié)合的方法對(duì)打緯機(jī)構(gòu)及墻板的振動(dòng)特性進(jìn)行研究。分析四連桿打緯機(jī)構(gòu)的動(dòng)力學(xué)特性，基于有限元法分析四連桿打緯力對(duì)織機(jī)墻板振動(dòng)的影響，建立打緯機(jī)構(gòu)的曲柄旋轉(zhuǎn)角度與打緯力、織機(jī)墻板最大振動(dòng)應(yīng)力和加速度的關(guān)系，確定織機(jī)墻板上最大振動(dòng)以及最大應(yīng)力產(chǎn)生的位置。結(jié)果表明，墻板發(fā)生共振的頻率約為44.5 Hz，與噴氣織機(jī)主振頻率非常接近，墻板的最大振動(dòng)主要集中在打緯機(jī)構(gòu)附近，而最大應(yīng)力主要集中在墻板中部和下部，并非墻板的最大振動(dòng)處。

噴氣織機(jī)； 打緯機(jī)構(gòu)； 有限元法； 振動(dòng)特性

機(jī)械振動(dòng)是一種常見(jiàn)的物理現(xiàn)象，通常情況下振動(dòng)的存在會(huì)影響機(jī)器的正常運(yùn)轉(zhuǎn)，還會(huì)引發(fā)噪聲及環(huán)境污染。隨著噴氣織機(jī)轉(zhuǎn)速的提高，織機(jī)四連桿打緯機(jī)構(gòu)引起的振動(dòng)和噪聲日益影響織機(jī)的正常運(yùn)轉(zhuǎn)。研究結(jié)果顯示，轉(zhuǎn)速為600 r/min時(shí)，織機(jī)墻板的最大振動(dòng)加速度達(dá)16 m/s2，實(shí)測(cè)噪聲超過(guò)86 dB，而噪聲的無(wú)害區(qū)小于60 dB，噴氣織機(jī)的噪聲遠(yuǎn)遠(yuǎn)超過(guò)了噪聲的無(wú)害區(qū)，員工在噪聲超過(guò)85 dB的環(huán)境中，將導(dǎo)致噪聲性耳聾[1]。

國(guó)內(nèi)外不少學(xué)者借助MatLab/Simulink[2]、SolidWorks simulation[3]等工具，以及其他特殊的方法，比如ODS法[4]，對(duì)織機(jī)機(jī)架或墻板進(jìn)行模態(tài)分析和振動(dòng)分析，建立了織機(jī)機(jī)架振動(dòng)的有限元模型[5]和劍桿織機(jī)墻板有限元模型[6]，用于研究機(jī)架或墻板的材料、結(jié)構(gòu)和剛度等對(duì)織機(jī)振動(dòng)的影響。通過(guò)改變機(jī)架或墻板的材料、結(jié)構(gòu)和質(zhì)量，來(lái)減輕織機(jī)的振動(dòng)。馮偉、沈丹峰等[7-8]專門(mén)對(duì)LL680織機(jī)進(jìn)行動(dòng)態(tài)特性測(cè)試，分析機(jī)構(gòu)的薄弱環(huán)節(jié)，以及織機(jī)結(jié)構(gòu)的高速動(dòng)態(tài)特性。本文在已有的研究基礎(chǔ)上將噴氣織機(jī)四連桿打緯機(jī)構(gòu)與墻板相結(jié)合，分析打緯機(jī)構(gòu)對(duì)墻板振動(dòng)產(chǎn)生的影響，包括打緯機(jī)構(gòu)動(dòng)力學(xué)分析、墻板模態(tài)分析、墻板應(yīng)力分析以及加速度分析，并與實(shí)驗(yàn)相結(jié)合，期望為噴氣織機(jī)打緯機(jī)構(gòu)的優(yōu)化提供理論參考和改進(jìn)方向。

1 噴氣織機(jī)打緯機(jī)構(gòu)分析

噴氣織機(jī)四連桿打緯機(jī)構(gòu)的打緯過(guò)程可分為打緯行程和空行程。為了節(jié)省空回的時(shí)間，要求空行程快速返回；打緯過(guò)程又需要很大的力，則要求較低的速度獲得較大的打緯力，這樣機(jī)構(gòu)便具有了急回運(yùn)動(dòng)的特性。圖1示出具有急回特性的曲柄搖桿機(jī)構(gòu)簡(jiǎn)圖。

圖1中θ為極位夾角，其數(shù)學(xué)表示公式為

(1)

(2)

θ=∠C1AD-∠C2AD

(3)

所以行程速比系數(shù)K，計(jì)算式為

(4)

式中：Td為打緯行程所需要的時(shí)間；Tk為空行程所需的時(shí)間。

打緯機(jī)構(gòu)對(duì)墻板的沖擊載荷是導(dǎo)致噴氣織機(jī)墻板振動(dòng)的主要因素，為研究作用力對(duì)墻板振動(dòng)的影響，根據(jù)四連桿機(jī)構(gòu)的結(jié)構(gòu)簡(jiǎn)圖建立曲柄、牽手和筘座的理論動(dòng)力學(xué)模型，其受力分析如圖2所示。

應(yīng)用達(dá)朗貝爾原理，列出圖2所示曲柄的動(dòng)力學(xué)方程為

(5)

(6)

(7)

式中：FAx和FAy為曲柄A端作用力；FBx和FBy為曲柄B端的作用力；m1為曲柄的質(zhì)量；a1x為曲柄x方向加速度；a1y為曲柄y方向加速度；W1為曲柄的重力；Md為曲柄的轉(zhuǎn)矩；S1為曲柄的質(zhì)心。

同理可列出牽手的動(dòng)力學(xué)方程：

(8)

(9)

(10)

式中：FBx和FBy為牽手B端的作用力；FCx和FCy為牽手C端的作用力；m2為牽手的質(zhì)量；a2x為牽手x方向加速度；a2y為牽手y方向加速度；W2為牽手的重力；-JS2α為牽手的慣性力矩；S2為牽手的質(zhì)心。

(11)

(12)

(13)

式中：FCx和FCy為筘座腳C端的作用力；FDx和FDy為筘座腳D端的作用力；m2為牽手的質(zhì)量；a3x為筘座腳x方向加速度；a3y為筘座腳y方向加速度；W3為筘座腳的重力；-JS3α為筘座腳的慣性力矩；S3為牽手曲柄的質(zhì)心。

將以上3組動(dòng)力學(xué)方程整理為矩陣的形式：

(14)

簡(jiǎn)寫(xiě)為

(15)

對(duì)上式進(jìn)行求解可得各作用力為

(16)

因此曲柄座的支反力FRAx=FAx、FRAy=FAy；筘腳座的支反力FRDx=FDx，F(xiàn)RDy=FDy。

2 四連桿機(jī)構(gòu)的動(dòng)力學(xué)仿真

圖3示出曲柄支座和筘座腳支座的支反力。曲柄轉(zhuǎn)速為600 r/min，從圖中的B1點(diǎn)開(kāi)始順時(shí)針旋轉(zhuǎn)，旋轉(zhuǎn)周期為0.1s。利用動(dòng)力學(xué)仿真得到四連桿機(jī)構(gòu)對(duì)墻板的沖擊力FRAx、FRAy、FRDx和FRDy。由圖可知當(dāng)曲柄轉(zhuǎn)角接近180°時(shí)，沖擊力達(dá)到最大值。

打緯力隨著曲柄旋轉(zhuǎn)角度的變化，呈現(xiàn)周期性變化，打緯力的周期與曲柄旋轉(zhuǎn)周期一致。曲柄從圖1的B1點(diǎn)開(kāi)始順時(shí)針旋轉(zhuǎn)，當(dāng)曲柄轉(zhuǎn)角接近180°時(shí)，x方向的沖擊力達(dá)到最大值。其中曲柄支座的x方向支反力約為15 000 N，筘座腳支座的x方向支反力約為20 000 N。說(shuō)明筘座腳支座的支反力對(duì)墻板振動(dòng)的影響更大。因此筘座腳支座慣性力和慣性力矩的優(yōu)化可以減小墻板的沖擊載荷，減小振動(dòng)和噪聲。

3 織機(jī)墻板振動(dòng)動(dòng)態(tài)特性分析

3.1 模態(tài)分析

由于織機(jī)墻板空間質(zhì)量的分布和各點(diǎn)均具有不同的變形，將墻板作為一連續(xù)系統(tǒng)模型來(lái)處理[10]。將墻板連續(xù)系統(tǒng)離散為多自由度的系統(tǒng)，對(duì)于織機(jī)墻板這種具有微小位移的多自由度彈性系統(tǒng)，其無(wú)阻尼自由振動(dòng)方程為

(17)

式中：[M]為墻板系統(tǒng)的質(zhì)量矩陣；[K]為墻板系統(tǒng)的剛度矩陣；{X}為廣義的位移列向量。

織機(jī)墻板的自由振動(dòng)為簡(jiǎn)諧振動(dòng)，則位移為正弦函數(shù)：

(18)

式中：X為振幅矩陣；φ為初始相位角；ω為頻率。

將式(18)對(duì)時(shí)間2次求導(dǎo)，得到廣義加速度矩陣

(19)

將式(18)和(19)代入式(17)得

(20)

表1示出噴氣織機(jī)墻板的前十階固有頻率。圖4示出噴氣織機(jī)墻板的前兩階振型。圖4(a)為一階振型；圖4(b)為二階振型。當(dāng)頻率為45.209Hz時(shí)，前、后下梁向外彎曲，最大彎曲位置為梁的中間部位；當(dāng)頻率為45.627Hz時(shí)，前下梁向內(nèi)彎曲，后下梁向外彎曲，最大彎曲位置也為梁的中間部位。此二階固有頻率下的位移幅值都比較大，對(duì)墻板結(jié)構(gòu)影響最為嚴(yán)重。因此墻板發(fā)生共振的頻率為44.5Hz左右，與噴氣織機(jī)主振頻率較為接近，使得織機(jī)墻板更容易產(chǎn)生共振，導(dǎo)致實(shí)際工作中墻板振動(dòng)強(qiáng)烈。

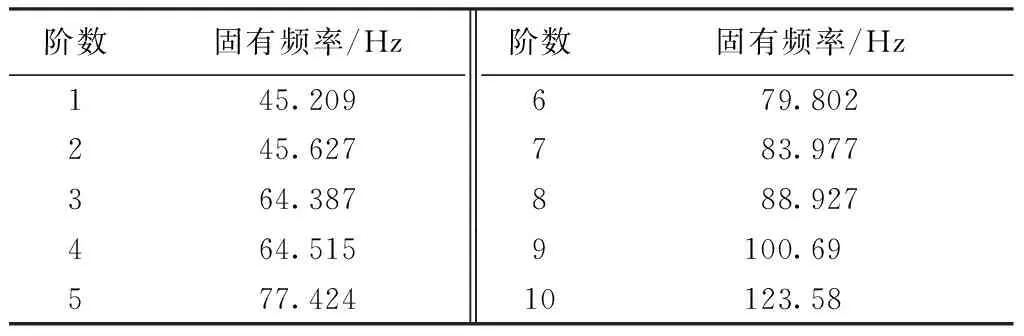
表1 噴氣織機(jī)墻板前十階固有頻率

3.2 應(yīng)力分析

von Mises應(yīng)力是一個(gè)集中了三維應(yīng)力狀態(tài)的6個(gè)應(yīng)力分量的應(yīng)力度量值。對(duì)于一個(gè)微元體而言，可由3個(gè)主應(yīng)力分量來(lái)描述，即σ1、σ2和σ3它們的方向垂直于微元體表面。根據(jù)第四強(qiáng)度理論，von Mises應(yīng)力可以表示為

(21)

由圖(3)、(4)可知沖擊力呈周期性變化，在0～0.025、0.025～0.050、0.050～0.075和0.075～0.100s下分別對(duì)墻板進(jìn)行動(dòng)態(tài)應(yīng)力仿真。由于墻板上有軸、梁的安裝孔位以及其他的孔位，為了避開(kāi)這些孔位，在墻板上均勻布置7個(gè)檢測(cè)點(diǎn)，分別為A、B、C、D、E、F和G，并在墻板上加上四連桿機(jī)構(gòu)的支反力，如圖5所示。仿真得到每個(gè)點(diǎn)隨曲柄旋轉(zhuǎn)角度變化的應(yīng)力大小，結(jié)果如圖6所示。

由應(yīng)力分析圖可知，當(dāng)曲柄從B1開(kāi)始旋轉(zhuǎn)，旋轉(zhuǎn)到B2(即打緯行程)，墻板各點(diǎn)的應(yīng)力值處于大致上升的過(guò)程，其中G點(diǎn)的應(yīng)力最大，應(yīng)力集中最嚴(yán)重，而D點(diǎn)的應(yīng)力最小。其中打緯行程中，墻板各點(diǎn)應(yīng)力最集中的時(shí)間段是在曲柄旋轉(zhuǎn)到B2附近，而并非是沖擊力最大的時(shí)間段。噴氣織機(jī)打緯機(jī)構(gòu)旋轉(zhuǎn)速度高，造成交變應(yīng)力集中頻繁，給噴氣織機(jī)墻板帶來(lái)巨大的危害。當(dāng)曲柄從B2開(kāi)始旋轉(zhuǎn)，旋轉(zhuǎn)到B1(即空行程)，墻板各點(diǎn)的應(yīng)力瞬間減小很多。空行程過(guò)程，墻板受力較小，相比而言A點(diǎn)的應(yīng)力最大，而不再是G點(diǎn)，因此打緯過(guò)程墻板應(yīng)力主要集中在A點(diǎn)和G點(diǎn)這塊區(qū)域。

3.3 加速度分析

仿真得到每個(gè)點(diǎn)隨曲柄旋轉(zhuǎn)角度變化的加速度，如圖7所示。

由加速度分析圖可知，當(dāng)曲柄從B1開(kāi)始旋轉(zhuǎn)到B2(即打緯行程)，墻板各點(diǎn)的加速度值處于波動(dòng)上升的過(guò)程，其中D點(diǎn)的加速度最大，振動(dòng)劇烈，而B(niǎo)點(diǎn)的加速度最小。打緯行程中，墻板振動(dòng)幅值最大的時(shí)間段主要集中在曲柄旋轉(zhuǎn)到B2附近，并非是沖擊力最大的時(shí)間段。

當(dāng)曲柄從B2開(kāi)始旋轉(zhuǎn)到B1(即空行程)，回轉(zhuǎn)的瞬間D點(diǎn)的加速度達(dá)到最大值15 m/s2。隨后墻板各點(diǎn)的加速度明顯減小許多。空行程過(guò)程D點(diǎn)的加速度最大，因此，打緯過(guò)程中墻板振動(dòng)最劇烈的部位主要集中D和E點(diǎn)附近。

4 實(shí)驗(yàn)驗(yàn)證

圖8示出墻板振動(dòng)加速度測(cè)試原理圖。當(dāng)轉(zhuǎn)速為600 r/min時(shí)，對(duì)某噴氣織機(jī)進(jìn)行振動(dòng)加速度實(shí)驗(yàn)測(cè)試。結(jié)果顯示，最大振動(dòng)加速度產(chǎn)生在D點(diǎn)，約為16 m/s2。仿真得到的最大振動(dòng)加速度也產(chǎn)生在D點(diǎn)，約為15 m/s2，與實(shí)驗(yàn)結(jié)果相符。

5 結(jié) 論

本文以噴氣織機(jī)四連桿打緯機(jī)構(gòu)為研究對(duì)象，對(duì)其打緯機(jī)構(gòu)振動(dòng)噪聲源分析，對(duì)其織機(jī)墻板振動(dòng)仿真，得出打緯機(jī)構(gòu)的曲柄旋轉(zhuǎn)角度與打緯力、織機(jī)墻板最大振動(dòng)應(yīng)力和加速度及其區(qū)域分布的關(guān)系等，結(jié)果表明：

1)打緯力隨著曲柄旋轉(zhuǎn)角度的變化呈周期性變化，打緯力的周期與曲柄旋轉(zhuǎn)周期一致。當(dāng)曲柄轉(zhuǎn)角接近180°時(shí)，沖擊力達(dá)到最大值。其中筘座腳支座的支反力的峰值大于曲柄支座的支反力的峰值，因此，筘座腳支座慣性力和慣性力矩的優(yōu)化可以很好的減小墻板的沖擊載荷，減小振動(dòng)和噪聲。

2)墻板發(fā)生共振的頻率為44.5 Hz左右，與噴氣織機(jī)主振頻率非常接近。優(yōu)化織機(jī)墻板結(jié)構(gòu)，改變墻板的彈性模量和質(zhì)量可改變墻板的固有頻率，使其固有頻率偏離噴氣織機(jī)主振頻率，避免發(fā)生強(qiáng)烈的共振。

3)應(yīng)力分析顯示，打緯過(guò)程墻板應(yīng)力主要集中在A點(diǎn)和G點(diǎn)附近，因此，有效地改善點(diǎn)和點(diǎn)附近的結(jié)構(gòu)，可以很好地減小應(yīng)力集中對(duì)噴氣織機(jī)墻板帶來(lái)的危害。

4)加速度分析顯示，墻板振動(dòng)最劇烈的區(qū)域主要集中在D和E點(diǎn)附近，即打緯機(jī)構(gòu)附近，因此，通過(guò)在D和E點(diǎn)附近涂阻尼層、安裝減振裝置等方法，可以很好地減小振動(dòng)和噪聲。

FZXB

[1] MINJA B M, MOSHI N H, RIWA P. Noise induced hearing loss among industrial workers in dares salaam[J]. East African Medical Journal, 2003, 80(6): 298-302.

[2] JIN Xin, HE Yulin, LIU Hua. Vibration analysis of wind turbine based on Pitt-Peter theory[J]. Engineering Mechanics, 2008, 25(7): 28-34.

[3] PAUL Kurowski. Engineering Analysis with SolidWorks Simulation 2013[M]. Kansas: Schroff Development Corp, 2013:10-50.

[4] 吳鋒, 張升陛. 織機(jī)機(jī)架結(jié)構(gòu)動(dòng)態(tài)特性分析及織機(jī)運(yùn)轉(zhuǎn)狀態(tài)下的振動(dòng)分析[J]. 機(jī)械科學(xué)與技術(shù), 1997, 16(3): 464-469. WU Feng, ZHANG Shengbi. Dynamic characteristics analysis on loom frame structure and loom vibration analysis under operation condition[J]. Mechanical Science and Technology, 1997, 16(3): 464-469.

[5] 薛元, 李風(fēng)強(qiáng). 織機(jī)機(jī)架振動(dòng)有限元分析[J]. 青島大學(xué)學(xué)報(bào), 1998, 13(2): 41-47. XUE Yuan, LI Fengqiang. Finite element analysis of the loom framework vibration[J]. Journal of Qingdao University, 1998, 13(2): 41-47.

[6] 宋梅利, 吳小平, 王公廉，等. 劍桿織機(jī)振動(dòng)問(wèn)題的有限元模態(tài)響應(yīng)分析[J]. 蘇州大學(xué)學(xué)報(bào), 2003, 23(1): 58-62. SONG Meili, WU Xiaoping, WANG Gonglian, et al. Rapier loom vibration finite element modal response analysis of the problem [J]. Journal of Soochow University, 2003, 23(1): 58-62.

[7] 馮偉, 張秋菊, 管仁偉. L680撓性劍桿織機(jī)動(dòng)態(tài)特性測(cè)試研究[J]. 機(jī)械設(shè)計(jì)與制造, 2010(1): 120-122.

FENG Wei, ZHANG Qiuju, GUAN Renwei. Dynamic characteristics testing of L680 flexible rapier loom[J]. Machinery Design & Manufacture, 2010(1): 120-122.

[8] 沈丹峰, 趙寧, 張華安，等. 織機(jī)四連桿打緯機(jī)構(gòu)對(duì)主墻板的動(dòng)應(yīng)力分析[J]. 紡織學(xué)報(bào), 2013, 34(1): 110-115. SHEN Dangfeng, ZHAO Ning, ZHANG Hua′an, et al. Dynamic stress analysis of four-bar linkage beating-up mechanism on loom wallboard[J]. Journal of Textile Research, 2013, 34(1): 110-115.

[9] WANG Yiqian, SI Hongzong, SU Yimin, et al. High speed dynamic characteristics research for L680 flexible rapier loom[J]. Materials Science and Engineering, 2013, 851(850): 274-278.

[10] WEN B C, ZHANG H, LIU S Y. Theory and Techniques of Vibrating Machinery and Their Applica-tions[M]. Beijing: Science Press, 2010: 1-50.

Vibration characteristics of wallboard and four-bar linkage beating-up mechanism of air-jet loom

JIN Yuzhen， HU Xiaodong， LIN Peifeng， HU Xudong

(FacultyofMechanicalEngineeringandAutomation，ZhejiangSci-TechUniversity,Hangzhou,Zhejiang310018,China)

For four-bar linkage beating-up mechanism of the air-jet loom, strong vibrations and noise will be caused by the increased speed. In this paper, the vibration characteristics of beating-up mechanism and wallboard were analyzed by theoretical analysis, numerical simulation and experiments. Firstly, the dynamic characteristics of the four-bar linkage beating-up mechanism were analyzed. And the influence of the four-bar linkage beating-up mechanism on the vibration of the loom wallboard was analyzed based on the finite element method. Through analysis, the relationship of the crank angle of rotation and the forces of beating-up mechanism, the maximum vibration stress and acceleration of loom wallboard were established. Lastly, the location of the maximum vibration and the maximum stress were determined. The results show that the resonance frequency of the wallboard is about 44.5 Hz, which is very close to the main vibration frequency of the air jet loom. The maximum vibration of the loom wallboard is mainly concentrated near the beating-up mechanism. However, the maximum stress is mainly concentrated near the middle and lower part of the loom wallboard instead of the largest vibration of the loom wallboard.

air-jet loom； beating-up mechanism; finite element method； vibration characteristics

10.13475/j.fzxb.20150601607

2015-06-09

2016-04-05

國(guó)家自然科學(xué)基金項(xiàng)目(51576180，51206149)；浙江省自然科學(xué)基金項(xiàng)目(LZ14E050004)；浙江理工大學(xué)流體工程技術(shù)創(chuàng)新團(tuán)隊(duì)項(xiàng)目(11132932611309)；浙江理工大學(xué)研究生創(chuàng)新研究項(xiàng)目(YCX14026)

金玉珍(1979—)，女，副教授，博士。主要研究方向?yàn)榧徔椦b備。E-mail：gracia1101@foxmail.com。

TS 103.3

A