熱油管道結蠟厚度與經濟清管周期計算

王繼平 王馨藝 郝寶健 等

摘 要：對熱油管道來說，結蠟到一定厚度時，易造成清管過程中蠟堵事故的發生。另外，結蠟還對熱油管道的經濟運行存在兩方面的影響，即增加動力費用和降低熱力費用。因此合理預測熱油管道的結蠟厚度和經濟清管周期尤為重要。介紹了一種普適性結蠟模型和經濟清管周期計算模型，在此基礎上以日均運行費用最低為目標，開發了熱油管道結蠟厚度與經濟清管周期預測程序，并以鐵嶺—新民段管線為例計算說明。指出了該程序的不足和今后研究方向。

關 鍵 詞：熱油管道；結蠟；經濟清管周期；運行費用

中圖分類號：TE 832 文獻標識碼： A 文章編號： 1671-0460（2016）03-0545-04

Abstract： For hot oil pipelines， wax plugging accident easily happens when the wax deposition reaches a certain thickness. The wax deposition has two aspects of effect on the economic operation of waxy hot oil pipeline， including increasing the power cost and reducing the heating cost. So it is especially important to predict wax deposition thicknesses and economic pigging cycles of hot oil pipeline. In this paper， a general wax model and an economic pigging cycle model were introduced， and prediction program of the wax deposition thickness and economic pigging cycle was developed by using average daily operating minimum charges as the target. Taking Tieling-Xinmin pipeline calculation as a case， the calculation was carried out. Meanwhile， the shortage of this program and the direction of the future research were pointed out.

Key words： Hot oil pipeline； Wax deposition； Economic pigging cycle； Operating cost

我國所產原油80%以上為含蠟原油，世界范圍內含蠟原油的產量也在不斷增加[1]，此類原油輸送主要采用加熱輸送工藝。熱油管道由于油溫與管壁溫度的差異很容易結蠟，當結蠟到一定厚度時，在清管過程中易造成蠟堵事故發生，對管道的安全運行產生嚴重的威脅。另外，結蠟還對管道運行費用有兩方面相互矛盾的影響：一方面結蠟會減小有效管徑，增大流動阻力，從而增加動力費用；另一方面結蠟能減小管道傳熱系數，降低散熱損失，從而降低熱力費用[2]。在一個清管周期內管道運行費用主要包括：動力費用、熱力費用以及一次性清管費用。隨著運行時間延長，結蠟增厚導致每天動力費用增加熱力費用降低，同時平均到每天的清管費用也降低，因而必然存在某個時間使得管道每天平均運行費用最低，該時間段即為經濟清管周期。因此合理估算管道結蠟厚度與經濟清管周期對于熱油管道的經濟安全運行顯得尤為重要。

1 蠟沉積模型介紹

蠟沉積模型的建立是基于蠟沉積機理、影響因素與實驗方法研究的基礎之上的。國內外對蠟沉積機理的研究已經有相當長的時間，對其認識也基本成熟。目前，蠟沉積主要考慮分子擴散、剪切彌散、重力沉降、布朗運動四種機理，更多關于蠟沉積機理介紹的可參考文獻[3，4]。對于蠟沉積的影響因素，普遍認為油溫、原油與管壁溫差、原油組成、剪切速率等是其主要影響因素[5，6]。除了以上理論的研究，模型的建立還依賴于試驗方法，主流的實驗方法包括：冷指法[7]、旋轉圓盤法[8]、環道法[9]。

基于以上理論研究與試驗方法，國內外學者對原油蠟沉積進行了系統研究， 提出了多個的蠟沉積模型[10-12]。黃啟玉[13]在分析了這些模型優缺點的基礎上，基于其實驗研究結果，提出了一個普適性結蠟模型，并利用該模型預測中銀線管道結蠟情況，與現場數據對比平均誤差僅為6.32%。劉楊等[14]利用該模型研究了大慶原油兩個聯合站之間管道結蠟規律。王鳳輝等[15]利用該模型分析了阿賽管道輸送不同原油時的結蠟情況。可見，該模型在預測國內熱油管道結蠟規律上得到了普遍認可。

在文獻[13]中利用逐步線性回歸的方法建立了適合含蠟原油的結蠟模型如下：

（1）

式中，k、m、n為常數，通過線性回歸得到。利用該模型，預測任意熱油管道結蠟規律需要確定的參數和大致計算過程如下：

（1）線性回歸得到k、m、n，得到具體的結蠟模型；

（2）利用蘇霍夫公式，計算沿線油溫；

（3）根據熱平衡關系，確定管線運行條件下不同管段的徑向溫度梯度，具體計算公式如式（2）所示：

（2）

（4）依據牛頓流體紊流狀態下的管壁剪切率公式（3），計算管壁剪切率；

（3）

（5）依據原油粘溫關系計算不同溫度下原油粘度；

（6）根據各管段的平均油溫，計算不同管段管壁處蠟分子濃度梯度；

（7）計算原油密度；

（8）由試驗測得的蠟晶溶解度系數與溫度關系曲線（ ）進行插值計算管壁處蠟晶的溶解度系數；

（9）由公式（4）計算結蠟后的總傳熱系數。

（4）

2 經濟清管周期

所謂經濟清管周期是指按照管道平均日運行費用最低的標準確定的清管時間。對于熱油管道來說，運行費用包括：動力費用、熱力費用以及一次性清管費用。

在一個清管周期內，隨著結蠟厚度的增加，管道的有效流通面積減小，油流流速增加，沿程摩阻增加，動力費用上升；同時，由于結蠟厚度的增加，管道的總傳熱系數減小，沿線溫降變緩，出站溫度可以適當的降低，從而使得管道的熱力費用減小（假設進站溫度一定）。因此計算過程需要考慮結蠟厚度對管道動力費用和熱力費用兩個因素的影響。另外一次性清管費用是固定的，隨著清管周期的延長，平均到每天的費用越小。將以上三個因素耦合，可以得到平均運營費用的最低點，該點對應的天數即為經濟清管周期。具體計算過程如下：

以1 d為單位計算結蠟速率，分天計算動力費用和熱力費用，再加上平均到每天的清管費用，找到費用最低點即可判斷為經濟清管周期。

（1）動力費用：

式中： SP — 單位為（元/d）；

ed — 電力價格，元/（kW·h）；

H — 泵站提供的揚程，m；

G — 輸量，t/d；

ηpe — 泵機組效率。

（2）熱力費用：

式中： SR — 單位為（元/d）；

cy — 油品的比熱容，kJ/（kg·℃）；

ηR —加熱爐效率；

ey — 燃料油價格，元/噸；

BH — 燃料油熱值，kJ/kg；

G — 輸量，t/d。

（3）總平均費用： （元/d）

式中：SP — 平均每天的動力費用，元/d；

SR —平均每天的熱力費用，元/d；

SQ — 一次清管費用，元；

day —運行天數，d。

3 計算程序介紹

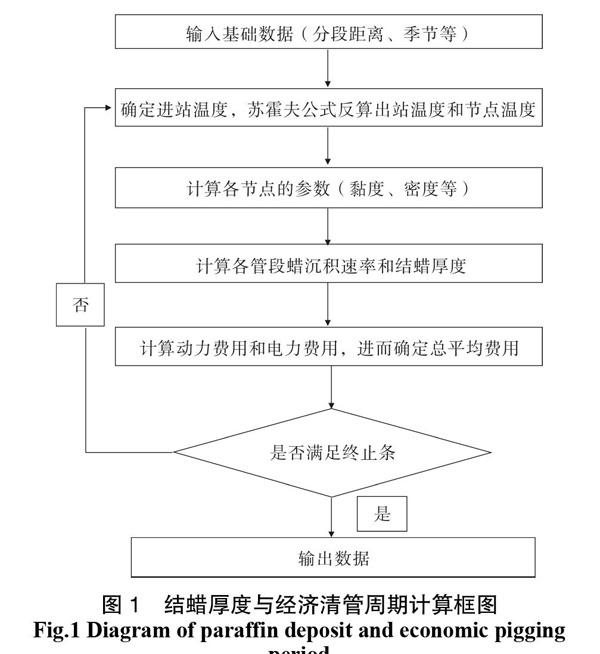
基于以上的理論分析和計算過程介紹，開發了含蠟原油管道結蠟厚度與清管周期計算程序。該程序適用不同季節的計算，在輸入界面需要輸入的參數包括：管道分段距離、季節、計算時間等，經過程序運行，可輸出數據包括：各站進出站溫度、管壁結蠟厚度和經濟清管周期等。

運算過程中默認第一天的結蠟厚度為0，而此以后計算新一天的結蠟厚度時，均取前一天蠟沉積厚度進行累積計算。程序輸出的蠟沉積厚度為輸入天數累積的厚度。輸出的熱力費用和電力費用值，都是假設在該天進行清管，以往每天的平均動力費用和熱力費用。

計算過程采用迭代算法，具體計算過程為：首先將管道分成距離為1 km的小段，設定進站油溫已知，根據蘇霍夫公式計算上個1 km處的溫度，然后將此溫度當做上1 km的進站溫度依次向上計算，直至計算到出站溫度為止。依據公式 計算每段的平均油溫，然后確定每一下段在平均溫度下的物性參數，包括：粘度、密度、徑向溫度梯度、管壁剪切率、蠟分子溶解度系數、總傳熱系數等，利用結蠟速率公式計算結蠟速率，進而求出結蠟厚度。計算框圖如圖1所示。

4 計算案例

以鐵秦線鐵嶺—新民段冬季運行為例，利用以上程序，模擬該段管道沿線蠟沉積分布規律與經濟清管周期。鐵嶺—新民全線距離92.19 km，輸量

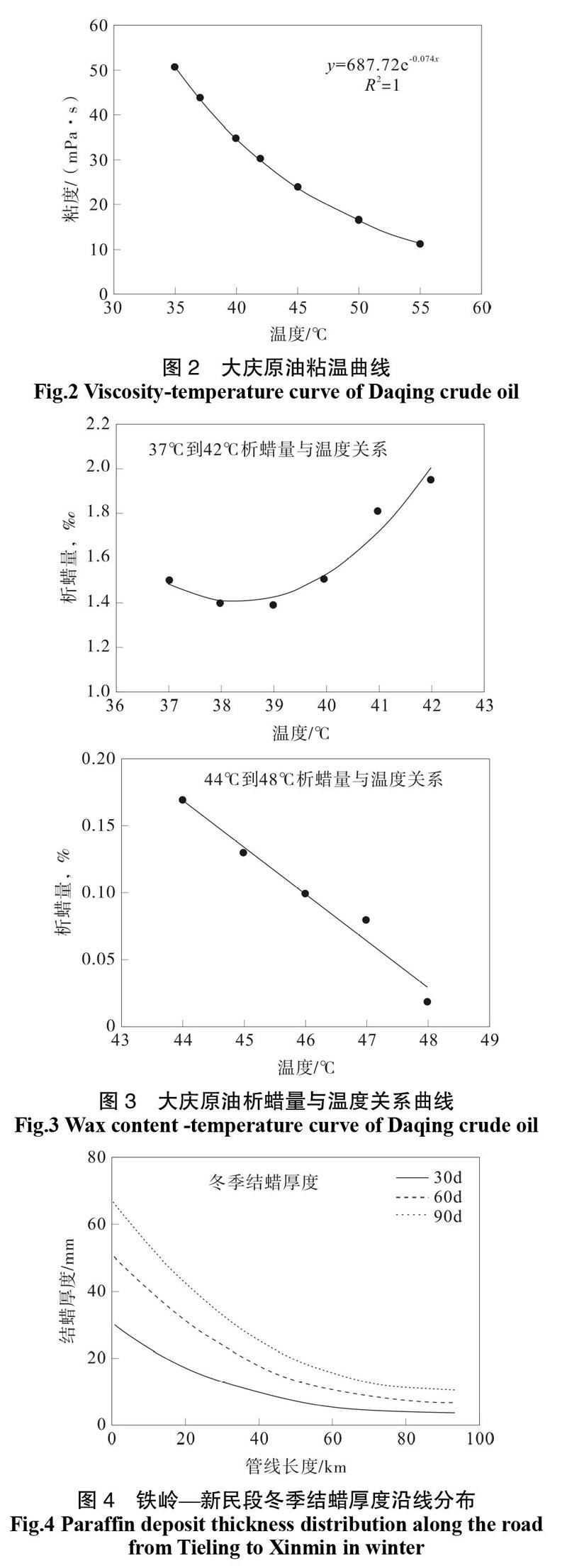
4 000 t/d，冬季低溫-5 ℃。其他相關數據如下：管徑：720 mm×8 mm；原油熱容：2 150 J/（kg·℃）；原油燃燒熱：41 400 kJ/kg；原油價格：3 200元/t；加熱爐的效率：88%；泵效率：81%；電費：0.60元/（kW·h）；一次清管費用：6 500元；20 ℃密度：852.5 kg/m3；最低進站溫度：37 ℃；最高出站溫度：67℃；蠟沉積層的導熱系數：0.135 W/（m·℃）；管輸原油結蠟速率[16]： ；黏溫關系如圖2所示；析蠟量與溫度關系如圖3所示。

通過程序計算得到鐵嶺—新民段冬季結蠟厚度沿線分布規律與日平均費用分別如圖4，圖5所示。

從圖4可看出，鐵嶺站入口處結蠟厚度最大，沿線結蠟厚度不斷減小。這是由于進站油高與管壁的溫差大，隨著原油向前流動過程中不斷散熱，原油與管壁溫差變小，結蠟速率降低。從圖5可看出，在現階段油價和相應運行參數下，該段管線冬季的經濟清管周期為80 d。

5 結束語

蠟沉積對熱油管道的安全、經濟運行有著重要的影響，國內外學者在蠟沉積機理研究的基礎上，提出了很多蠟沉積計算模型。但是，能夠直接適用于國內熱油管道蠟沉積預測的并不多，直到文獻[13]提出一種普適性的蠟沉積模型。目前，該模型已經被用來預測國內多條熱油管道的蠟沉積情況。

任何一條管道，在安全的基礎上都要求經濟利益最大化，因此就有了經濟清管周期概念的提出。筆者在借鑒普適性結蠟模型的基礎上，引入經濟清管周期計算模型，開發了含蠟原油結蠟厚度與經濟清管周期預測程序，并以鐵嶺—新民段管線為例計算說明。

當然，該計算程序并未考慮清管之后余蠟厚度的影響。同時，由于季節參數的不同該程序還不能用來預測全年的結蠟情況，一次計算只能用來預測一個季度的情況。這些都是今后開發更普適性計算方法的方向。

參考文獻：

[1]張勁軍.易凝高黏原油管輸技術及其發展[J].中國工程科學，2002，4（6）：71-76.

[2]周詩崠，王樹立，趙會軍，等.熱含蠟原油管道經濟清蠟周期計算[J].油氣儲運，2006，25（8）：15-17

[3]Burger E D，Perkins T K，Striegler J H，et al.Studies of Wax Deposition in the Trans-Alaska Pipeline[J].Journal of Petroleum Technology，1981，33（6）：1075-1086.

[4]Bern P，Withers V，Cairns R.Wax Deposition in Crude Oil Pipelines[C].European Offshore Technology Conference & Exhibition，1980.

[5]黃啟玉，張勁軍，嚴大凡.一種新的蠟沉積模型[J].油氣儲運，2003，22（11）：22-25.

[6]胡志勇，吳明，酆春博，等.保溫原油管道蠟沉積研究綜述[J].當代化工，2013，42（9）：1312-1315.

[7]Hamouda A，Viken B K.Wax deposition mechanism under high-pressure and in presence of light hydrocarbons[C]. SPE 25189，1993.

[8]Matlach W J，Newberry M E，Matlach W J，et al.Paraffin Deposition and Rheological Evaluation of High Wax Content Altamont Crude Oils[C].SPE Rocky Mountain Regional Meeting，1983.

[9]Singh P，Ramachran Venkatesan，Fogler H S，et al.Formation and aging of incipient thin film wax-oil gels[J].Aiche Journal，2000，46（5）：1059–1074.

[10]Burger E D，Perkins T K，Striegler J H， et al.Studies of Wax Deposition in the Trans Alaska Pipeline[J].Journal of Petroleum Technology，1981，33（6）：1075-1086.

[11]Hamouda A，Ravney J.Prediction of Wax Deposition in Pipelines and Field Experience on the Influence of Wax on Drag-Reducer Performance[C].Offshore Technology Conference，1992.

[12]Hsu J J C，Brubaker J P.Wax Deposition Scale-Up Modeling for Waxy Crude Production Lines[C].Offshore Technology Conference，1995.

[13]黃啟玉，李瑜仙，張勁軍.普適性結蠟模型研究[J].石油學報，2008，29 （3）：459-462.

[14]劉揚，王志華，成慶林，等.大慶原油管輸結蠟規律與清管周期的確定[J].石油學報，2012，33（5）：892-897.

[15]王鳳輝，曹月明，韓繼強.阿賽管道蠟沉積速率模型與計算實例[J].油氣儲運，2015，34（4）：395-399.

[16]黃啟玉，張勁軍，高學峰，等.大慶原油蠟沉積規律研究[J].石油學報，2006，27（4）：125-129.