基于主成分分析的區域初始水權分配

吳振 邵東國 顧文權

摘要：在遵循有效性、公平性和可持續性原則構建初始水權分配指標體系的基礎上，針對初始水權分配中指標體系存在顯著的相關性和權重偏好非一致性等問題，提出將主成分分析應用于初始水權分配中以消除相關性的影響。該方法先用主成分分析法對指標體系進行賦權，之后結合改進AHP與熵權法對多層次指標體系進行組合賦權，以消除單一權重方法的片面性，并利用博弈論進行指標權重的綜合集成，最后運用綜合評價法確定初始水權進行分配權重。將此方法用于湖北省應城市的初始水權分配，結果分析表明，采用該方法進行初始水權分配可行且合理。該方法可以為其他區域的初始水權分配提供參考和借鑒，并為水資源的統一管理奠定了基礎。

關鍵詞：初始水權分配；主成分分析；熵權法；改進的AHP；綜合集成

中圖分類號：TV211 文獻標志碼：A 文章編號：1672-1683（2016）04-0179-06

Abstract：The index system of the initial water rights allocation was constructed following the principle of effectiveness，equity and sustainability.Aiming at the problems of significant correlation of index system and inconsistency of weight preference of initial water rights allocation，Principle Component Analysis （PCA） was applied to the initial water rights allocation to eliminate the impact of correlation.In the method， firstly，Principle Component Analysis （PCA） was proposed to empower the index system，Thereafter，improved AHP and entropy method were adopted to determine weights for multi-lever index system，which eliminated the unilateral result.And game theory was used to carry out the comprehensive integration of index weight.Finally， a comprehensive evaluation method was used to allocate initial water rights.The method was applied to study the initial water rights allocation in Yingcheng，Hubei province.The verification of the model and the analysis of the experimental results showed that the proposed method worked well and was rational and practical.The model could provide a reference for initial water rights allocation in other areas and lay the foundation for the unity management of the water resources.

Key words：initial water rights allocation；principal component analysis；entropy method；improved AHP；comprehensive integration

中國經濟社會的迅速發展使中國資源型、工程型、水質性缺水問題并存，水資源供需矛盾日趨顯著，嚴重制約了中國經濟社會的可持續發展。而解決水資源短缺問題的最有效途徑是建立以水權、水市場和水權交易制度為基礎的水資源管理體系[1]。流域初始水權分配則是進行水資源管理的首要前提，也是實現水資源高效利用和優化配置的有效舉措。

目前，初始水權分配的研究成果多是對分配原則和指標體系作定性的描述，而對初始水權可操作性定量分配研究較少[2-5]。指標權重的科學確定是進行水資源初始水權定量分配的關鍵一步，因此運用相關原理和方法確定指標權重對于評價結果的合理性起著至關重要的作用。國內目前對指標權重的確定方法主要有主觀賦權方法和客觀賦權方法[11-16，19-20]，主觀賦權法體現了專家的意愿偏好，客觀賦權法反映了具體數據對評價結果的貢獻度。但是，由以上單一的主觀或客觀賦權法計算得到的權重值僅考慮了個體指標的特征，對多個評價對象的相互聯系卻無法描述，而且不能解決指標信息高度重疊和高度相關的問題。主成分分析法利用指標間的相互關系，通過變量變換實現具有相關性指標信息的綜合，在盡可能不損失原指標信息的情況下消除評價指標間的相關影響，但其在確定權重時用方差貢獻率做權重，包含主觀成分，且會損失部分信息量。熵值法利用信息熵值來確定指標的權重，并且在計算過程中沒有減少變量個數，因此更為客觀，但是卻過于依賴數據的聚集程度。

為解決上述問題，本文將主成分分析[7-9]引入初始水權分配的計算中，結合改進AHP與熵權法，利用博弈論[10]對指標體系進行綜合集成賦權，最后采用綜合評價法計算初始水權分配比例，以提高初始水權分配結果的準確度。

1 基于主成分分析的初始水權分配方法步驟

通過有效的集結不同計算方法的優點可以減小不同方法之間的差異，提高初始水權分配結果精度。根據同一對象不同的計算方法其計算結果應該具有一致性這一基本條件，可以用KENDALL-W協和系數作為檢驗手段，利用博弈論將主成分分析法和熵值法與AHP這些單一的主客觀計算方法進行綜合集成求得指標權重，并運用綜合評價法求得初始水權分配比例。

1.1 主成分分析法

（1）標準化處理。

對指標進行標準化處理[8]時，首先采用均值化法將原始數據無量綱化處理。對于正向型指標，其計算公式為

（2）主成分分析。

對標準化處理后的指標值進行主成分分析，根據計算得出的矩陣特征值和相應的方差貢獻率，利用“因子荷載量為主成分相應特征值的平方根與特征向量的乘積”計算特征向量，從而得到主成分線性表達式為

1.2 一致性檢驗

KENDALL-W協和系數法是考查m種評價方法對n個對象的評判結果之間是否一致，協和系數W表示樣本數據中實際符合與最大可能符合之間的分歧程度。其計算公式為：

1.3 基于博弈論的綜合集成賦權

博弈論的基本思想是在不同的權重之間尋找一致或妥協，極小化理想的綜合權重與各個基本權重之間的偏差，盡可能保留各權重值的信息。運用博弈論對指標值進行綜合集成形成新的指標權重，具體方法如下。

使用L種方法對評價指標進行賦權，L個基本權重集向量的任意線性組合為

式中：ω為基于基本權重集的一種可能的綜合權重向量。為了選擇出一個最滿意的權重ω*，使ω和各個基本權重向量之間的偏差極小化，需要對式（5）中L個線性組合系數βk進行優化，優化目標是使ω與各個ωk的離差最小，即：

1.4 基于主成分分析的初始水權分配步驟

（1）由改進的AHP[13]確定準則層的權重，并由熵權法[14-18]確定目標層的權重向量，之后根據公式（8）求出最終指標權重向量ω1。

（2）由主成分分析法確定指標權重向量ω2。

（3）若由主成分分析確定的指標權重向量與由AHP、熵值法確定的指標權重向量能通過一KENDALL-W協和系數致性檢驗，則利用博弈論將ω1和ω2進行綜合集成賦權，得指標綜合權重向量ω。

（4）采用綜合評價法計算初始水權分配比例，公式如下：

2 實例應用

2.1研究區概況

湖北省應城市水資源多年平均水資源總量為5.5億m³，利用率低，且年際變化較大，水質性缺水問題嚴重。其中大富水年最大水資源量為10.6億m³（1998年），年最小水資源量為1.56億m³（2011年），最大與最小之比為9.2倍。應城市當地徑流主要來源于降水，多年平均降雨量1 109.4 mm。年徑流深336.8 mm，年徑流系數0.324，年徑流模數為35.55萬m³/km²。從水資源的時空和總量分布看，應城市是一個水資源比較貧乏的地區。全市水資源多年人均日占有量為0.24 m³/（人·日），畝均日占有量為0.26 m³/（畝·日），均低于湖北省水平。

2.2 指標體系的建立

通過分析應城市的水資源供需態勢，為客觀反映應城市的實際現狀，遵循指標選取的科學性、代表性、獨立性、層次性等原則，本文參考現有文獻[11，12]并基于有效性原則、公平性原則和可持續性原則，建立了包含13個指標的指標體系（表1）。其中人均生活用水量、農田灌溉單位面積用水量和萬元工業增加值用水量為逆向指標。

2.3 基于AHP和熵權法賦權的指標權重的確定

應城市的初始水權分配指標體系是一個二級層次指標體系。在本研究中，準則層對目標層權重的確定采用改進AHP法，措施層對準則層權重的確定采用熵權法賦權。

2.3.1 準則層對目標層的權重確定

根據應城市的實際情況，有效性比公平性更重要，公平性比可持續性更重要。采取標度值P12=1.3，P13=1.69，構造判斷矩陣：

2.3.2 指標層對準則層的權重確定

根據初始水權分配指標體系和應城市各計算區的實際資料，確定各計算區的指標值，將由指標值構成的原始矩陣進行極大值標準化，結果見表1，由熵權法計算出的熵和熵權值見表2。

2.3.3 層次總排序

由式（8）計算出指標權重向量，并歸一化處理ω1，見表2。

2.4 基于主成分分析法的指標權重的確定

將應城市11個計算區的各指標數據進行標準化處理后作為樣本，利用SPSS Statistic 19.0對其進行主成分分析。根據主成分相應的特征根>1，且累計方差貢獻率≥80%的原則，來提取主成分因子（見表3）。主成分與對應變量的相關系數組成的因子荷載矩陣見表4。利用公式（3）計算各指標權重并歸一化得ω2，其結果見表4。

2.5 利用博弈論進行綜合集成賦權

首先采用式（4）對以上兩種綜合評價方法進行一致性檢驗，計算協和系數W為0.9409，χ²為18.8182，顯然χ²>χ²0.05（10）=18.31。從而可以認為在置信度為95%的情況下兩種求權結果具有一致性，可以對這兩種結果進行集成綜合評價。

將上述兩權重ω1和ω2代入式（7），計算出ω1和ω2的系數分別為：β1=0.6218，β2=0.4973。歸一化得β1=0.5556，β2=0.4444。將β1、β2及ω1、ω2代入式（5）得各指標綜合權重為：（0.1088 0.0739 0.1135 0.0786 0.0666 0.0784 0.0765 0.0749 0.0528 0.1296 0.0612 0.0306 0.0545）。

2.6 初始水權分配結果與分析

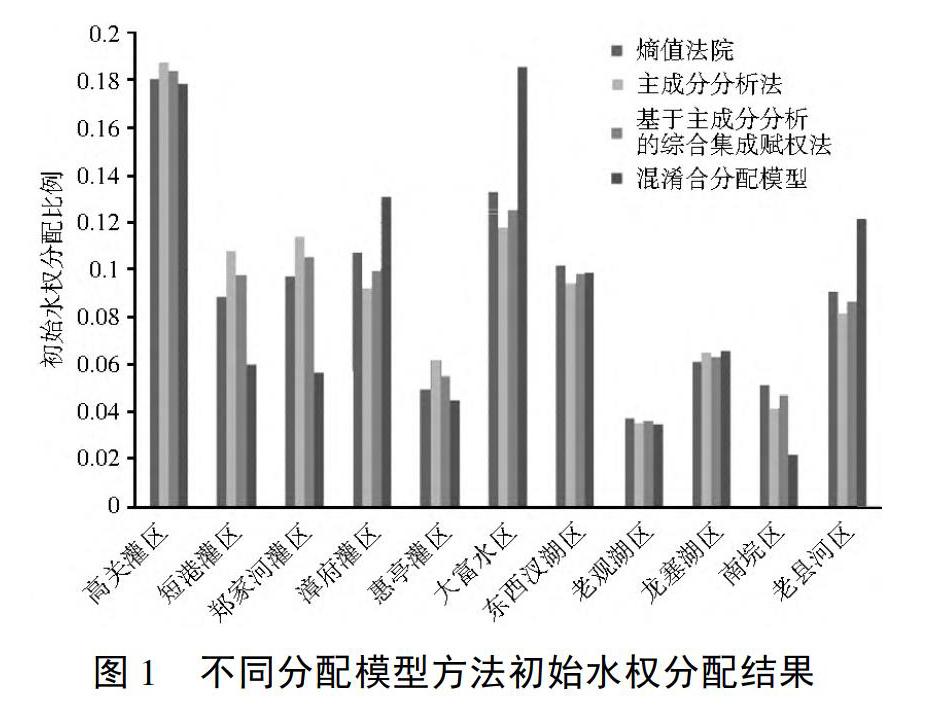
根據式（9）得到應城市各計算區初始水權分配比例的結果為：高關灌區（0.1843）、短港灌區（0.0979）、鄭家河灌區（0.1054）、漳府區（0.1003）、惠亭灌區（0.0554）、大富水區（0.1257）、東西汊湖區（0.0982）、老觀湖區（0.0363）、龍賽湖區（0.0631）、南垸區（0.0469）、老縣河區（0.0865）。

為驗證基于主成分分析的初始水權分配的合理性，本文與熵值法、主成分分析法、混合分配模型計算的結果進行對比分析（圖1）：雖然結果不盡相同，但是整體具有一致性，（高關灌區、大富水區、東西汊湖區、漳府區和老縣河區初始水權較多），說明本文提出的方法可以應用于初始水權分配。

熵值法有機結合了AHP和熵權法，保留了決策者在評價過程中的主觀導向，又基于比較嚴格的數學理論和方法來確定權重。根據該法計算結果：，權重最大的指標是林果地面積，主要是因為其各計算區原始數據值差異較大。熵值法得到的分配比例排在前6位的分別是高關灌區（0.1808）、大富水區（0.1327）、漳府區（0.1075）、東西汊湖區（0.1018）、鄭家河區（0.0976）和老縣河區（0.0907）。主成分分析法得到的分配比例排在前6位的是高關灌區（0.1881）、大富水區（0.1181）、鄭家河區（0.1141）、短港灌區（0.1079）、東西汊湖區（0.0941）和漳府區（0.0922）。混合模型計算結果相差較大，這是因為該模型只選取了以按面積和農業需水量兩個指標進行分配，因素考慮較為單一，不能代表所有的信息量。而本文提出的基于主成分分析綜合集成賦權的初始水權分配方法是前兩種方法的有機結合，更為全面合理。盡管4種方法模型的計算結果在變化趨勢、比例大小等方面表現出相對一致性，但對于個別計算區也存在一定差異，比如短港灌區和漳府區。應城市的工業、第三產業主要集中在大富水區，并且每年都保持一定的比例增長，同時高關灌區有效灌溉面積大，人口也相對較多。而本文提出的方法能將較多的初始水權分配到這兩個計算區，可以體現水資源初始水權分配中的有效性原則和公平性原則。針對應城市水資源相對短缺的現狀，在注重其用水效率的同時，更應統籌水資源利用的可持續發展。

3 結論

目前初始水權分配理論尚不完整，指標體系也不系統。為使計算結果更科學、合理、客觀，本文提出的基于主成分分析的初始水權分配方法，集結了主成分分析法和熵值法的優點，利用博弈論將這兩種方法計算的權重進行集化、融合，既可以充分利用數據的統計特征來反映實際情況，又能克服不確定性和片面性，解決了目前初始水權分配方法中指標之間存在相關性影響的問題，使結果可靠度更高。

本文根據應城市的實際情況，以數學統計分析法為前提，運用主成分分析法并結合熵值法計算權重，既能消除指標間的相關影響，又能減少異常值造成的結果偏差，而且用該方法得到的結果同其他方法的結果基本保持一致，說明采用該方法得到的結果具有一定的科學合理性，計算結果可信，可以為其他城市或流域的初始水權分配提供參考。

參考文獻（References）：

[1] 王浩，黨連文，謝新民，等.流域初始水權分配理論與實踐[M].北京：中國水利水電出版社，2008.（WANG Hao，DANG Lian-wen，XIE Xin-min，et al.Theory and practice on allocation of initial water rights in a watershed[M].Beijing：China Water & Power Press，2008.（in Chinese））

[2] 裴源生，李云玲，于福亮.黃河置換水量的水權分配方法探討[J].資源科學，2003，25（2）：32-37.（PEI Yuan-sheng，LI Yun-ling，YU Fu-liang.Discussion on water right allocation of replaced water from Yellow River[J].Resources Science，2003，25（2）：32-37.（in Chinese）

[3] 吳鳳平，葛敏.水權第一層次初始分配模型[J].河海大學學報： 自然科學版，2005，33（2）：216-219.（WU Feng-ping，GE Min.Initial allocation model for water right of the first hierarchy[J].Journal of Hohai University ：Natural Science，2005，33（2）：216-219.（in Chinese））

[4] 李海紅，趙建世. 初始水權分配原則及其量化方法[J].應用基礎與工程科學學報，2005，（增刊 1）：8-14.（LI Hai-hong，ZHAO Jian-shi.The principle of the initial right and the practice method[J].Journal of Basic Science and Engineering，2005，（Suppl.1）：8-14.（in Chinese））

[5] WANG Zhong-jing，ZHENG Hang，WANG Xue-feng.A harmonious water rights allocation model for Shiyang River Basin，Gansu province，China[J].International Journal of Water Resources Development，2009，25（2）：355-371.

[6] 郭顯光.一種新的綜合評價方法-組合評價法[J].統計研究，1995，12（5）：56-59.（GUO Xian-guang.A new combinational evaluation method：combine evaluation method[J].Statistical Research，1995，12（5）：56-59.（in Chinese））

[7] 朱雷.基于主成分分析法的揚州市生態環境質量評價[D].揚州：揚州大學，2013.（ZHU Lei.The study on evaluation of Yangzhou urban ecological environmental quality based on principal component analysis[D].Yangzhou ：Yangzhou University，2013.（in Chinese））

[8] 李浩鑫，邵東國，尹希，等.基于主成分分析和Copula函數的灌溉用水效率評價方法[J].農業工程學報，2015，31（11）：96-102.（LI Hao-xin，SHAO Dong-guo，YIN Xi，et al.Evaluation method for irrigation-water use efficiency based on principle component analysis and Copula function[J].Transactions of the Chinese Society of Agricultural Engineering（Transactions of the CSAE），2015，31（11）：96-102.（in Chinese））

[9] 趙麗，朱永明，付梅臣，等.主成分分析法和熵值法在農村居民點集約利用評價中的比較[J].農業工程學報，2012，28（7）：235-242.（ZHAO Li，ZHU Yong-ming，FU Mei-chen，et al.Comparative study on intensive use of rural residential land based on principal component analysis and entropy[J].Transactions of the Chinese Society of Agricultural Engineering（Transactions of the CSAE），2012，28（7）：235-242.（in Chinese））

[10] 郭燕紅，邵東國，劉玉龍，等.工程建設效果后評價博弈論集對分析模型的建立與應用[J].農業工程學報，2015，31（9）：5-12.（GUO Yan-hong，SHAO Dong-guo，LIU Yu-long，et al.Establishment and application of set pair analysis model based on game theory for post-assessment of project construction effectiveness[J].Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE），2015，31（9）：5-12.（in Chinese））

[11] 許國柱.基于AHP的三亞市初始水權分配[J].水利科技與經濟，2014，20（9）：52-55.（XU Guo-zhu.The initial water rights allocation of Sanya city based on AHP[J].Water Conservancy Science and Technology and Economy，2014，20（9）：52-55.（in Chinese））

[12] 尹云松，孟令杰.基于AHP的流域初始水權分配方法及其應用實例[J].自然資源學報，2006，2（4）：645-651.（YIN Yun-song，MENG Ling-jie.The method of basin initial water rights allocation and its application based on AHP[J].Journal of Natural Resources，2006，2（4）：645-651.（in Chinese））

[13] 倪九派，李萍，魏朝富，等.基于AHP和熵權法賦權的區域土地開發整理潛力評價[J].農業工程學報，2009，25（5）：202-209.（NI Jiu-pai，LI Ping，WEI Chao-fu，et al.Potentialities evaluation of regional land consolidation based on AHP and entropy weight method[J].Transactions of the Chinese Society of Agricultural Engineering，2009，25（5）：202-209.（in Chinese））

[14] 郭顯光.熵值法及其在綜合評價中的應用[J].財貿研究，1994（6）：56-60.（GUO Xian-guang.Application of entropy method in comprehensive evaluation[J].Finance and Trade Research，1994（6）：56-60.（in Chinese））

[15] 羅軍剛，解建倉，阮本清.基于熵權的水資源短缺風險模糊綜合評價模型及應用[J].水利學報，2008，39（9）：1092-1097.（LUO Jun-gang，XIE Jian-cang，RUAN Ben-qing.Fuzzy comprehensive assessment model for water shortage risk based on entropy weight[J].Journal of Hydraulic Engineering，2008，39（9）：1092-1097.（in Chinese））

[16] 郭顯光.改進的熵值法及其在經濟效益評價中的應用[J].系統工程理論與實踐，1998，18（12）：98-102.（GUO Xian-guang.Application of improved Entropy method in evaluation of economic result[J].Systems Engineering-Theory & Practice，1998，18（12）：98-102.（in Chinese））

[17] 張麗，宋士強，張艷紅.基于熵權的模糊物元模型在水權分配中的應用[J].人民黃河，2008，30（8）： 56-58.（ZHANG Li，SONG Shi-qiang，ZHANG Yan-hong.Application of fuzzy matter element based on coefficients of entropy in water rights allocation[J].Yellow River，2008，30（8）：56-58.（in Chinese））

[18] 郭顯光.熵值法及其在綜合評價中的應用[J].財貿研究，1994（6）：56-60.（GUO Xian-guang.Application of Entropy method in comprehensive evaluation[J].Finance and Trade Research，1994（6）：56-60.（in Chinese））

[19] 邵東國，陳會，李浩鑫.基于改進突變理論評價法的農業用水效率評價[J].人民長江，2012，43（20）：5-7.（SHAO Dong-guo，CHEN Hui，LI Hao-xin.Evaluation on agricultural water utilization efficiency based on catastrophe theory[J].Yangtze River，2012，43（20）：5-7.（in Chinese））

[20] 陳艷萍，吳鳳平，吳丹.基于模糊優選和 TOPSIS 法的流域初始水權分配模型[J].河海大學學報： 自然科學版，2009，37（4）：467-471.（CHEN Yan-ping，WU Feng-ping，WU Dan.Initial water rights allocation model for basins based on fuzzy optimization and TOPSIS methods[J].Journal of Hohai University：Natural Science，2009，37（4）：467-471.（in Chinese））