不同海潮模型對GNSS站負荷位移計算的影響

趙大江　郭春喜　程傳錄　陳　敏　史　旗

1　國家測繪地理信息局大地測量數據處理中心，西安市友誼東路334號，710054

不同海潮模型對GNSS站負荷位移計算的影響

趙大江1郭春喜1程傳錄1陳敏1史旗1

1國家測繪地理信息局大地測量數據處理中心，西安市友誼東路334號，710054

摘要：基于古登堡平均地球模型和積分格林函數方法，利用中國近海海潮模型Chinasea 2010、Naoregional 1999和全球海潮模型EOT11a，計算中國沿海GNSS連續運行站上的海潮位移負荷影響，并對其均方根RMS及和方根RSS進行綜合分析。結果表明，2種近海模型分潮波位移負荷差異水平分量大部分為亞mm級，垂直分量普遍為mm級，最大達5.8 mm；Chinasea 2010模型比Naoregional 1999模型在中國海域覆蓋面積大，2種模型在黃海和東海海域差異較大，在渤海和南海海域差異較小；模型差異與測站位置及潮波頻率均有關系，應比較觀測資料的負荷改正效果，擇優采用適宜本區域的模型。

關鍵詞：中國近海海潮模型；積分格林函數；GNSS連續運行站；位移負荷；位移負荷時間序列

太陽和月亮的引潮力作用使海水質量重新分布，地表荷載發生變化，引起固體地球產生形變[1-3]。潮汐效應使地面及內部質點產生位移和引力位變化，從而導致地面觀測值發生變化，使點的水平和高程位置有所改變。很多學者對海潮位移負荷進行了研究[4-7]。

近年來，隨著TOPEX/Poseidon、Jason-1/2、ERS-1/2等衛星測高數據、驗潮站觀測資料的豐富以及有限元方法的發展，新的中國近海潮汐模型被提出。由于我國海岸線數萬km，近海海岸形狀不規則，海底地形復雜、構造特殊，且各模型的構制方法、所使用的數據及資料不同，因此，各模型在不同海域的適用性差異較大，計算時應選擇適宜的近海模型進行修正。本文利用Chinasea 2010、Naoregional 1999兩種中國近海模型及EOT11a全球海潮模型[8-11]，基于積分格林函數方法，計算我國沿海GNSS連續運行站的位移負荷效應，并比較兩種近海模型在我國沿海不同區域的影響差異。

1海洋潮汐模型

表1是3種海洋潮汐模型的基本信息。其中，H是流體動力學模型，T/P是TOPEX/Poseidon測高數據，ERS是ERS測高數據，Jason是Jason測高數據，Envisat是Envisat測高數據，T/G是驗潮站的海潮數據。

表1　2種中國近海海潮模型及EOT11a全球海潮模型基本信息

2計算方法

2.1海潮位移負荷改正

海潮負荷由海潮的瞬時潮高與格林函數褶積積分求得，計算公式為：

(1)

式中，L(φ,λ)為海潮對站點位移負荷的影響，Dns(φ,λ)、Dew(φ,λ)和Dup(φ,λ)分別為位移負荷南北分量、東西分量和垂直分量，(φ,λ)和(φ′,λ′)分別為計算點和負荷點的球坐標,φ、φ′為余緯，λ、λ′為經度，R為地球半徑，ρ為海水密度，h(φ′,λ′)為(φ′,λ′)處的潮高(由海潮模型獲得)，θ為計算點到負荷點的表面角距離(通過cosθ=sinφsinφ′+cosφcosφ′cos(λ-λ′)求得)，A為計算點到負荷點的方位角，G(θ,A)為負荷格林函數。

當采用近海模型來修正全球海潮模型時，將全球海潮模型中的相應區域用近海潮汐模型替換，式(1)可變為：

(2)

式中，h(φ′,λ′)為近海區域SL的潮高。

采用積分格林函數計算時，將負荷域按角距劃分成若干子區間，認為在方位角相同的子區間內潮高相同，選定某1個潮波后，對方位角A進行數值積分。該方法較一般積分求和法精度高。通過積分，可得到測站位移的海潮負荷影響L(φ,λ)，然后在頻域求出任一分潮波位移改正的振幅和相位。疊加不同分潮波影響，即可得到測站位移海潮負荷改正：

(3)

式中，Lj(j=1,2,3)分別為測站東西、南北和垂直分量的海潮位移負荷影響，N為潮波數，Aji、φji為測站各分潮位移分量對應的振幅和相位，ωi、χ0為各分潮的角頻率和天文幅角初相。

2.2模型比較

通過均方根RMS及和方根RSS進行綜合比較分析，描述不同海洋潮汐模型之間的差異。根據式(4)、(5)，計算將2種近海模型修正到全球海潮模型后獲得的位移負荷結果的均方根RMS及和方根RSS：

(4)

(5)

式中，Ho、go、Hm、gm分別代表兩種近海海潮模型修正后的全球海潮模型在各測站點的振幅和相位，N為大地控制點個數，I為分潮波數。

3數值結果與分析

根據文中計算模型與方法，采用古登堡平均地球模型和積分格林函數法計算兩種近海模型對中國沿海均勻分布的26 個GNSS連續運行站位移負荷計算的影響。計算時，遠區顧及EOT11a全球海潮模型的影響。

M2、K1、O1、S2潮波位移負荷影響較大，限于篇幅，圖1僅給出M2潮波的位移負荷影響，其中橫坐標為沿我國海岸線各海域由北向南分布的GNSS連續運行站點，縱坐標為各站點位移負荷的振幅。M2潮波海潮位移負荷影響最大達19.4mm(Chinasea2010模型)，模型差異達5.8mm；黃海海域的煙臺、榮成站點，黃海及東海海域的江蘇、浙江沿海站點負荷影響東西分量差異大，最大為1.8mm；南北分量在黃海海域的煙臺及榮成站點差異最大，達3.8mm；垂直分量在黃海及東海海域部分站點差異較大，達5.8mm。南海海域各站點負荷影響東西分量、南北分量及垂直分量差異均較小。K1潮波負荷影響最大為8.1mm(naoregional1999模型)，模型差異最大為2.3mm；黃海及東海海域的江蘇、浙江沿海站點，南海海域站點負荷影響東西分量差異大，最大為0.5mm；南北分量在東海海域的站點差異較大，達2.3mm，垂直分量在黃海及東海海域部分站點差異較大，達1.8mm。O1潮波最大為6.9mm(Chinasea2010模型)，模型差異在青島最大，達1.3mm；黃海海域的榮成站點、東海海域和南海海域沿海站點東西分量差異大，最大為0.8mm；南北分量在渤海海域的站點差異較大，達1.0mm，垂直分量在黃海及東海海域部分站點差異較大，達1.3mm。S2潮波最大為5.4mm(Chinasea2010模型)，模型差異達2.8mm；東海海域的江蘇、浙江沿海站點負荷影響東西分量差異大，最大為0.6mm；南北分量在黃海海域的榮成站點差異較大，達1.1mm，垂直分量在黃海及東海海域部分站點差異大，達2.7mm。負荷分布復雜，位移負荷影響與測站位置相關。

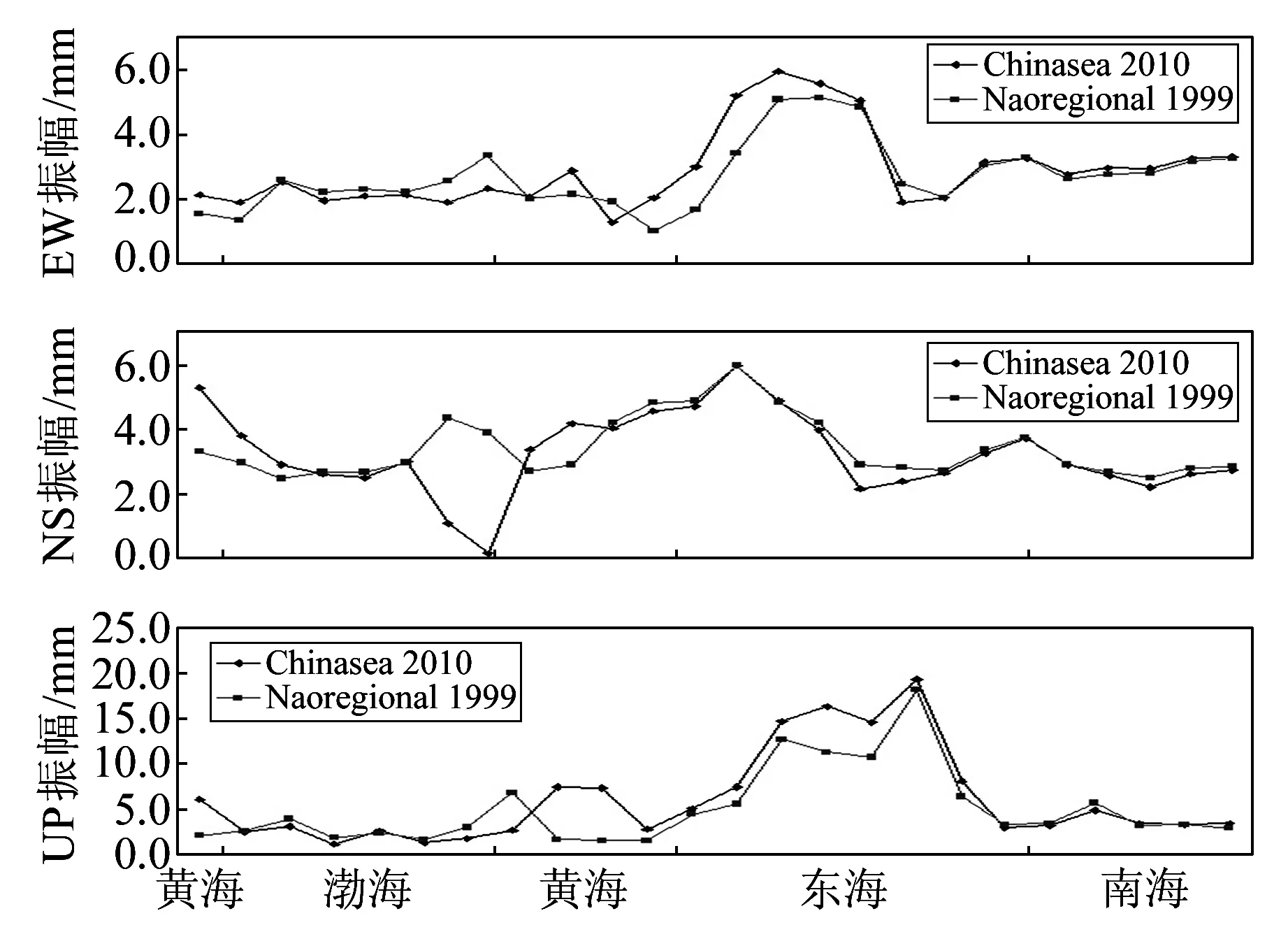
圖1　海洋潮汐對我國沿海GNSS連續運行站位移負荷的影響(M2潮波)Fig.1　The displacement loading effect of the ocean tides on the GNSS continuous operation reference station along China’s coastline(M2 wave)

應用式(4)、(5)計算我國不同海域GNSS連續運行站8個主要潮波(M2、S2、N2、K2、K1、O1、P1、Q1)東西分量、南北分量和垂直分量的RMS(均方根)與RSS(和方根)見圖2～5。

由圖2可知，渤海區域沿海站點(LNYK、LNHL、HETS、TJBH、HECX、SDYT)M2、S2、N2潮波南北分量差異接近垂直分量，M2潮波南北分量RMS為1.2mm，K1、O1潮波垂直分量RMS大于東西分量和南北分量，其余潮波南北分量大于東西分量。南北分量RSS為1.3mm，垂直分量RSS達到1.6mm。

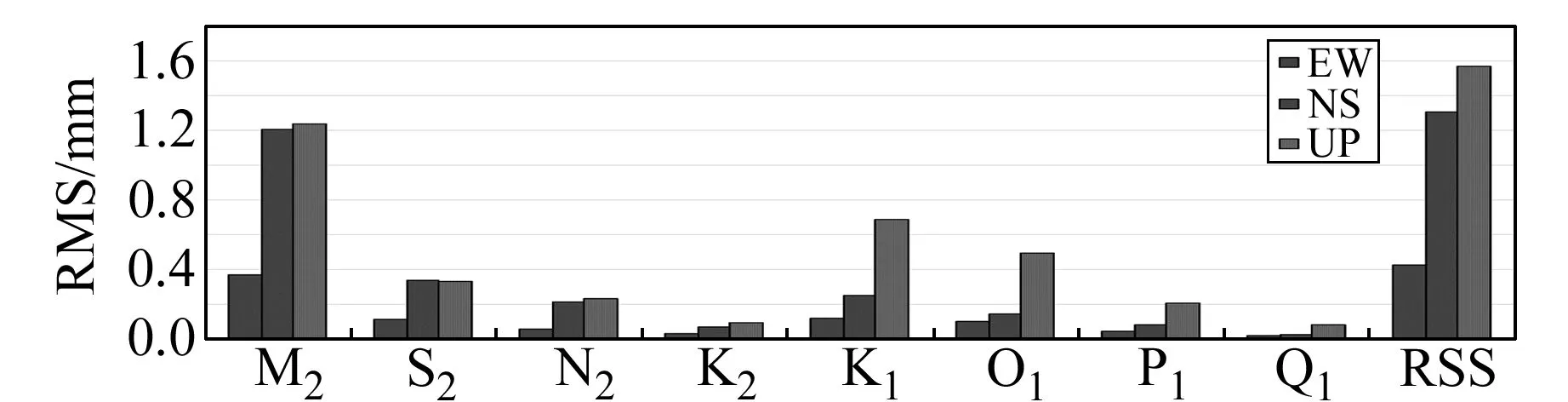
圖2　2種近海模型在渤海區域位移負荷影響的RMS和RSSFig.2　RMS and RSS of two China regional tide models in the Bohai Sea

由圖3知，黃海區域沿海站點(LNDD、SDRC、SDQD、JSLY、JSYC、JSNT)M2、S2、K1、O1潮波差異較大，且K1、O1、P1潮波東西分量較南北分量差異大，其余潮波南北分量差異大于東西分量，垂直分量差異M2潮波最大，RMS達到3.8mm。RSS南北分量為1.6mm,東西分量為1.4mm，垂直分量為4. 9mm。

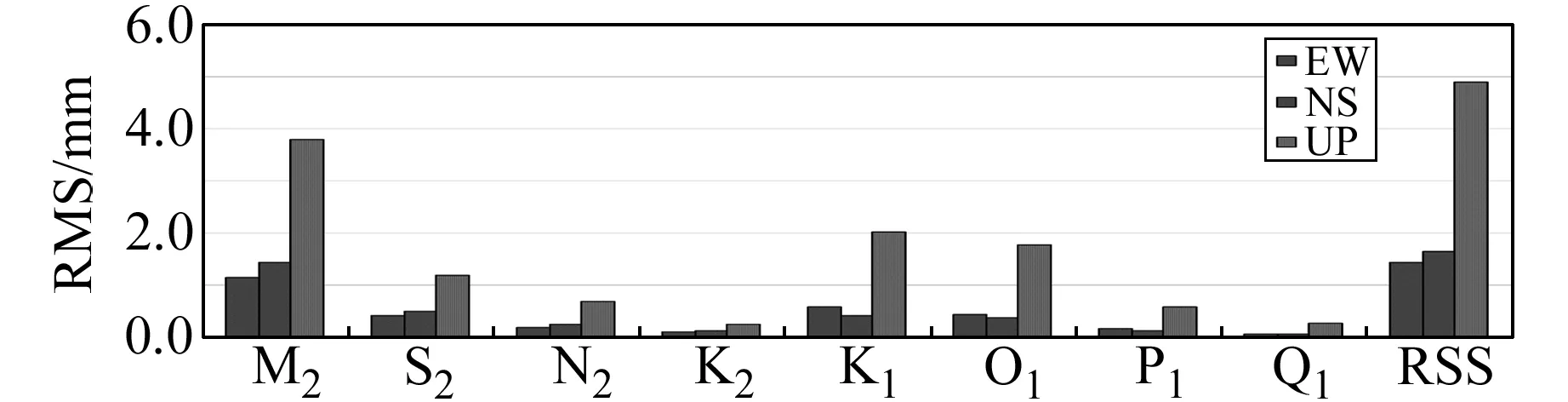
圖3　2種近海模型在黃海區域位移負荷影響的RMS和RSSFig.3　RMS and RSS of two China regional tide models in the Yellow Sea

由圖4知，東海區域沿海站點(SHAO、ZHZS、ZJWZ、FJXP、FJPT、XIAM、GDST)垂向分量均大于水平分量，M2潮波垂向分量RMS最大，為3.2mm，8個潮波水平分量RMS均小于1.0mm，K1、P1、Q1潮波南北分量略大于東西分量，其余潮波東西分量大于南北分量。東西分量RSS為0.9mm，南北分量RSS為0.7mm，垂向分量RSS達到3.7mm。

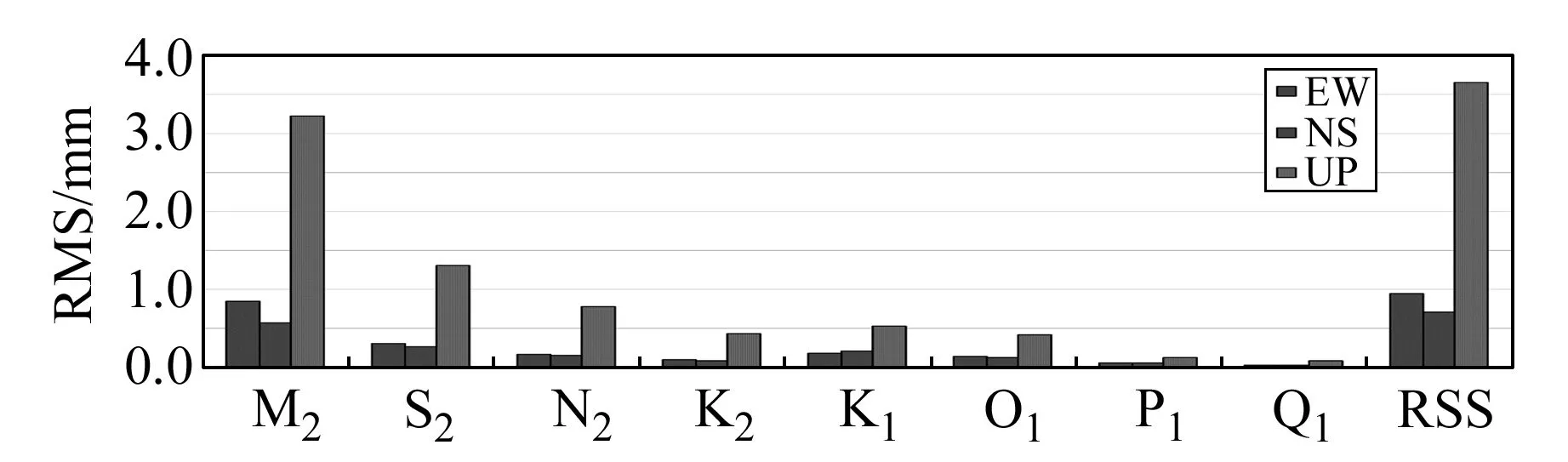
圖4　2種近海模型在東海區域位移負荷影響的RMS和RSSFig.4　RMS and RSS of two China regional tide models in the East China Sea

由圖5知，南海區域沿海站點(GUAN、GDZH、GDZJ、GXBH、HIHK、QION、HISY)RMS垂向分量均大于水平分量，K1潮波垂向分量最大，為0.3mm，8個潮波水平分量均小于0.2mm，Q1潮波東西分量略大于南北分量，其余潮波南北分量大于東西分量。東西分量RSS為0.2mm，南北分量RSS為0.3mm，垂向分量RSS達到0.6mm。

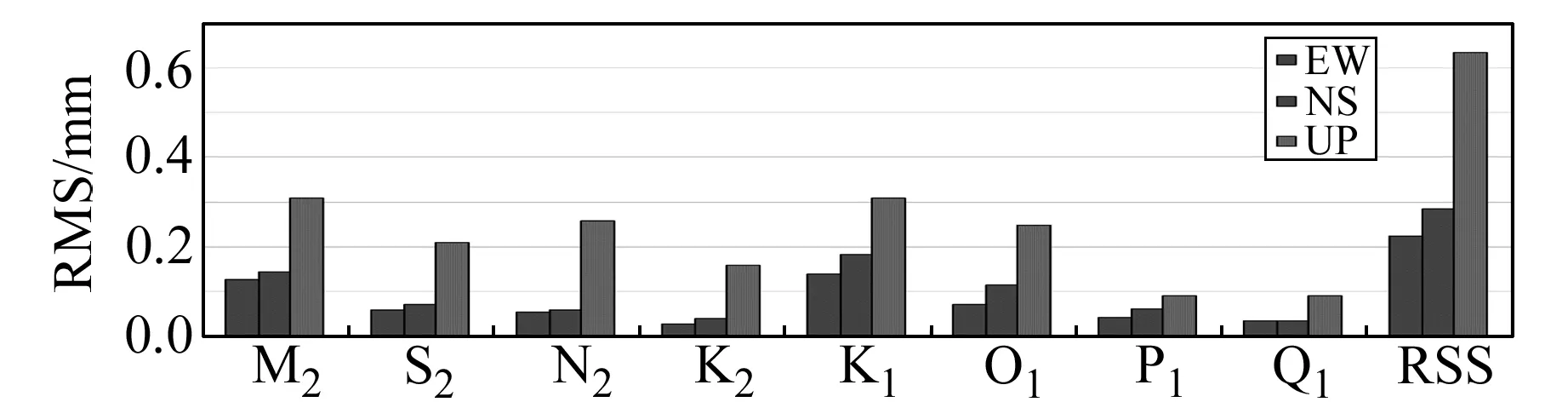
圖5　2種近海模型在南海區域位移負荷影響的RMS和RSSFig.5　RMS and RSS of two China regional tide models in the South China Sea

應用式(3)計算8個主要潮波對測站位移總的海潮負荷效應影響，圖6～9給出了我國沿海不同海域4個站點(LNHL、SDRC、ZJWZ和GDZH)2015-01-01～31兩種近海模型海潮位移負荷差異時間序列。

由圖6可知，渤海區域站點(LNHL)位移負荷差異時間序列變化趨勢垂直分量大于水平分量，垂直分量為0.001～1.765mm；南北分量大于東西分量，南北分量差異為0～0.617mm，東西分量為0.009～0.270mm。

圖6　2種近海模型修正的全球模型在渤海區域站點(LNHL)位移負荷影響Fig.6　The displacement loading effect of the modified global models in the Bohai Sea(LNHL)

由圖7可知，黃海區域站點(SDRC)位移負荷差異時間序列整體趨勢垂直分量最大，最大達到cm量級，為0.001～10.662mm。南北分量較東西分量差異大，東西分量差異為0.001～1.646mm，南北分量差異為0.005～5.799mm。

圖7　2種近海模型修正的全球模型在黃海區域站點(SDRC)位移負荷影響Fig.7　The displacement loading effect of the modified global models in the Yellow Sea(SDRC)

由圖8可知，東海區域站點(ZJWZ)位移負荷差異時間序列整體趨勢垂直分量遠大于水平分量，垂直分量差異接近cm量級，為0.025～9.572mm。東西分量較南北分量差異大，東西分量差異為0～1.933mm，南北分量差異為0.002～1.305mm。

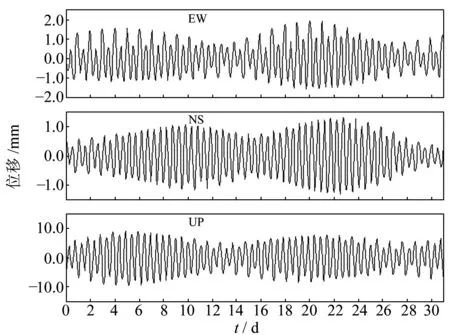
圖8　2種近海模型修正的全球模型在東海區域站點(ZJWZ)位移負荷影響Fig.8　The displacement loading effect of the modified global models in the East China Sea(ZJWZ)

由圖9可知，南海區域站點(GDZH)位移負荷差異時間序列整體趨勢南北分量比東西分量差異大，垂直分量最大。東西分量差異為0～0.089mm，南北分量差異為0～0.551mm，垂直分量差異為0.008～2.041mm。

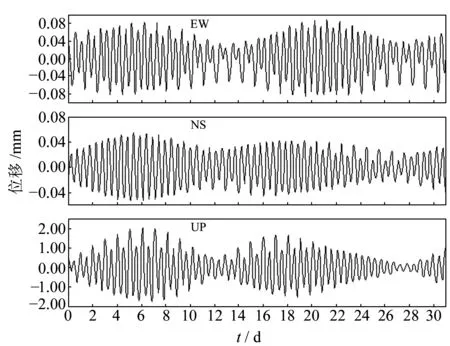
圖9　2種近海模型修正的全球模型在南海區域站點(GDZH)位移負荷影響Fig.9　The displacement loading effect of the modified global models in the South China Sea(GDZH)

4結語

近海區域的海潮負荷影響較大，GNSS觀測資料的處理要顧及近海潮汐效應。全球海洋潮汐模型在中國沿海的適用性較差，準確、高精度的近海模型更能反映我國局部海水的潮汐變化特征，獲得可靠的海潮位移負荷改正。

中國沿海M2、K1、O1、S2潮波位移負荷影響較大，最大達19.4mm。近海模型的位移負荷在沿海站點差異大，分潮波模型差異水平分量大部分為亞mm級，垂直分量差異大于水平分量，普遍為mm級，最大達5.8mm。總體來說，在我國黃海、東海海域沿海站點潮波影響差異較大，渤海及南海海域站點個別潮波分量差異大。K1、O1潮波在南海海域站點東西分量差異大，南北分量及垂直分量差異均較小；O1潮波在渤海海域的站點南北分量差異較大。位移負荷分布復雜，與測站位置相關。

8個主要潮波的RMS和RSS計算結果表明，在中國沿海大部分區域，2種近海模型垂直分量差異大于水平分量，各海域不同潮汐模型差異不一致。渤海與南海海域站點各潮波南北分量大于東西分量，黃海與東海海域站點部分潮波東西分量大于南北分量。黃海海域差異最大，南海海域差異最小，且Naoregional1999模型只覆蓋南海部分區域。從選取站點位移時間序列差異分析，水平分量均小于垂直分量，垂直分量在東海海域站點(ZJWZ)達到cm級；渤海、黃海和南海海域南北分量均大于東西分量，東海海域東西分量大于南北分量。綜合分析，Chinasea2010模型比Naoregional1999模型在中國海域覆蓋面積大，兩個模型在黃海與東海海域差異較大，在渤海與南海海域差異較小，模型差異與測站位置及潮波頻率均有關系；海潮位移負荷計算時，應分析所計算區域的模型差異，利用GNSS站觀測資料，比較不同模型負荷位移改正后坐標的RMS，確定適宜該站的海潮模型。

參考文獻

[1]LongmanIM.AGreen’sFunctionforDeterminingtheDeformationoftheEarthunderSurfaceMassLoads:Theory[J].JournalofGeophysicalResearch, 1962, 67(2): 845-850[2]周旭華,吳斌,李軍.高精度大地測量中的海潮位移改正[J].測繪學報，2001,30(4):327-330(ZhouXuhua,WuBin,LiJun.OceanTideDisplacementCorrectionsinHighPrecisionGeodesy[J].ActaGeodaetieaetCartographicaSinica, 2001, 30(4):327-330)

[3]周江存，孫和平.海潮負荷對GPS基線的影響[J].大地測量與地球動力學，2005,25(4):27-32(ZhouJiangcun,SunHeping.EffectofOceanTideLoadingonGPSBaselineMeasurement[J].JournalofGeodesyandGeodynamics, 2006, 25(4):27-32)

[4]鄭祎，伍吉倉，王解先, 等．海潮模型和格林函數對海潮位移改正的影響[J].大地測量與地球動力學，2002,22(4)：71-76(ZhengYi,WuJicang,WangJiexian.EffectofTideModelandGreenFunctiononOceanTidalDisplacementCorrection[J].JournalofGeodesyandGeodynamics, 2002,22(4):71-76)

[5]張捍衛，鄭勇，趙方泉．海洋負荷潮汐對測站位移影響的理論研究[J].大地測量與地球動力學，2003,23(1)：69-73(ZhangHanwei,ZhengYong,ZhaoFangquan.TheoreticalResearchofOceanLoadingTideInfluenceonStationDisplacements[J].JournalofGeodesyandGeodynamics, 2003,23(1):31-39)

[6]李大煒，李建成，金濤勇, 等．利用驗潮站資料評估全球海潮模型的精度[J].大地測量與地球動力學，2012,32(4)：106-110(LiDawei,LiJiancheng,JinTaoyong.AccuracyEstimationofRecentGlobalOceanTideModelsUsingTideGaugeData[J].JournalofGeodesyandGeodynamics, 2012,32(4):106-110)

[7]PennaNT,KingMA,StewartMP.GPSHeightTimeSeries:Short-PeriodOriginsofSpuriousLong-PeriodSignals[J].JournalofGeophysicalResearch:SolidEarth, 2007, 112(B2):1 074-1 086

[8]EgbertGD,ErofeevaSY.OTISReginalTidalSolutions[EB/OL].http://volkov.oce.orst.edu/tides/YS.html, 2010[9]MatsumotoK,TakanezawaT,OoeM.OceanTideModelsDevelopedbyAssimilatingTOPEX/POSEIDONAltimeterDataintoHydrodynamicalModel:AGlobalModelandaRegionalModelaroundJapan[J].JournalofOceanography, 2000, 56(5): 567-581

[10]ChengYC,AndersenOB.ImprovementinGlobalOceanTideModelinShallowWaterRegions[C].OST-STMeetingonAltimetryforOceansandHydrology,Lisbon, 2010

[11]趙大江，郭春喜，張世娟，等.中國沿海不同海潮模型的傾斜負荷分析[J].大地測量與地球動力學，2015,35(1):34-39(ZhaoDajiang,GuoChunxi,ZhangShijuan,etal.AnalysisofTiltLoadingwithDifferentOceanTideModelsinCoastalAreasofChina[J].JournalofGeodesyandGeodynamics, 2015, 35(1):34-39)

Foundation support:National Key Technology R&D Program,No.2012BAB16B01;National Natural Science Foundation of China,No.41574003.

About the first author:ZHAO Dajiang,engineer, majors in geodetic data processing,E-mail: yangtze393@126.com.

The Load Effect of Ocean Tide Models on Displacement at the GNSS Station

ZHAODajiang1GUOChunxi1CHENGChuanlu1CHENMin1SHIQi1

1Center for Geodetic Data Processing,NASMG, 334 East-Youyi Road, Xi’an 710054, China

Abstract:In view of the Gutenberg-Bullen average earth model and the integral Green’s function, load effects of ocean tide models on displacement at the GNSS continuous operation reference station along China’s coastline are calculated with the two China regional ocean tide models and global ocean tide model EOT11a. Furthermore, the root mean square (RMS) and root sum square (RSS) are comprehensive analyzed. The results show that most of the differences of horizontal displacement loading for the two models are in sub-millimeter, with millimeter magnitude for almost all the vertical displacement loading with a maximum of 5.8 mm. Meanwhile, the coverage area of Chinasea 2010 in the China Sea is larger than Naoregional 1999. There is a great difference between the two models in the Yellow Sea and the East China Sea, but in the Bohai Sea and the South China Sea the difference is small. As the differences among models are relevant to the station location and tidal wave frequency, we should compare the load correction of data and adopt the preferable model suitable for the particular studied areas.

Key words:China regional ocean tide models; integral Green’s function; GNSS continuous operation reference station; displacement loading; the displacement loading time-series

收稿日期：2015-07-14

第一作者簡介：趙大江，工程師，主要從事大地測量數據處理研究，E-mail: yangtze393@126.com。

DOI：10.14075/j.jgg.2016.07.021

文章編號：1671-5942(2016)07-0654-05

中圖分類號：P223

文獻標識碼：A

項目來源：國家科技支撐計劃(2012BAB16B01);國家自然科學基金(4154003)。