“導數的應用（一）”教學設計

姚貴豐郭桂芳

?

“導數的應用（一）”教學設計

姚貴豐郭桂芳

教材分析

教材內容：本節課是人教版高中數學選修2-2第一章第四節“生活中的優化問題舉例”第一課時，主要內容是用導數求生活中面積、體積的最值問題。

地位和作用：生活中的優化問題是在導數的概念、運算，用導數求極值、最值等內容的基礎上教學的，它既是對導數知識的復習鞏固，也是導數知識在實際生活中的應用。本節課以生活實例為題材，培養學生的閱讀能力和建模意識。學習過程中的認知沖突，不同思維的碰撞，易激發學生思維的積極性，有助于創新能力的培養。

學情分析：學生剛學完導數的概念、運算、用導數求極值、最值等知識，為用導數解決實際生活中的問題創造了條件。高二年級的學生正值身心發展的鼎盛時期，思維活躍，并有相應的認知基礎，樂于探索、敢于探究。但邏輯思維能力還屬于經驗型，運算能力不強，數學建模方法的運用還不夠熟練，有待進一步加強訓練。

教學目標

知識與技能：掌握利用函數思想、導數方法求有關面積、體積的最值問題。

過程與方法：以日常生活、生產實踐中典型的問題為載體，探討利用函數思想、導數方法求面積和體積問題的應用。

情感態度與價值觀：學生分享將實際問題轉化為數學問題的學習樂趣，感受數學與生活的密切聯系。

重點、難點

重點：從實際問題中抽象出函數模型，用導數方法求解函數最值問題的程序化步驟。

難點：對最值、最值與極值概念的區別與聯系的理解。

教學過程

一、創設情境，復習引入

以本班學生參加元旦匯演的圖片引入。K1303舉行了2016年的元旦迎新活動，數學興趣小組就活動前的海報設計和活動后海報的再利用進行了如下課題探究活動。下面我們一起再現他們的活動過程。

設計意圖：以學生成功的活動經歷引入，激起學生的學習興趣。

二、活動設計，培養創新思維

探究一：如果海報為如下圖所示的豎向張貼的海報，要求版心面積為128dm2，上、下兩邊各空2dm，左、右兩邊各空1dm。若海報版心高為xdm，

1.求四周空白面積關于x的函數解析式；

2.求四周空白面積最小值。

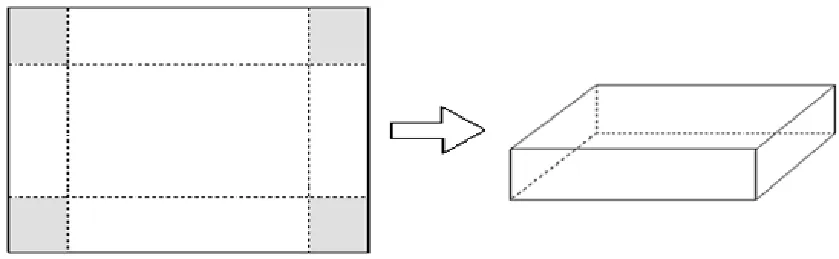
探究二：若海報材料用的是長20dm、寬10dm的長方形硬紙板，活動結束后，興趣小組準備將海報做成廢品收集箱進行再利用。如下圖所示，從長方形紙板的4個角上分別切去面積相等的正方形，再把紙板的邊沿虛線折起，用膠粘好，做成一個無蓋的長方體箱子。問廢品收集箱底面的長、寬分別是多少時，其容積最大，最大容積是多少。

探究三：興趣小組將另外兩張廢棄海報用膠紙拼成如下圖所示的邊長為20dm的正方形ABCD，切去陰影部分所示的4個全等的等腰直角三角形，再沿虛線折起，使得4個點重合于圖中的點P，正好形成一個正四棱柱形狀的包裝盒，E，F在AB上，是被切去的等腰直角三角形斜邊的兩個端點，設AE=FB=xdm。

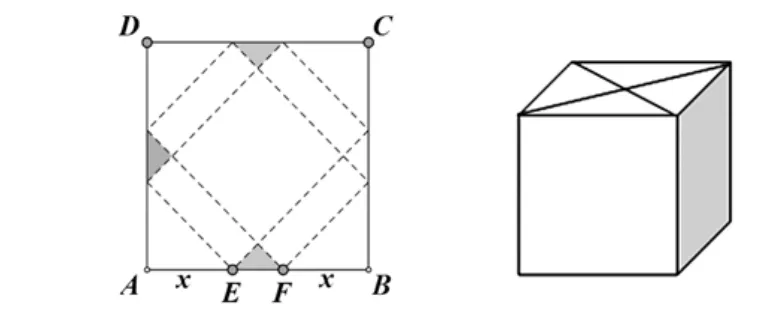
（1）包裝盒要顯得更大氣，因而要增大包裝盒的側面積。試問x取何值時，包裝盒的側面積S（dm2）最大？

（2）另一同學認為包裝盒要更適用，因而要使包裝盒的容積最大。但限于某種原因，x∈（0，c]，（c∈（0，10]的常數），試問x應取何值時，包裝盒容積V （dm3）最大？并求其最大值。

（3）先學后教，以學定教

教師讓學生欣賞元旦匯演的圖片后，引入探究一。學生思考后進行解答。觀察到學生用基本不等式求解面積最值時，教師抓住契機提出問題，引入導數作為工具，求面積、體積的最值。教學探究三時，教師讓學生先分組討論，然后概括思路，再由學生作答。教師通過實物投影儀當堂評價，并就學生學習中出現的問題進行現場講評，做到舉一反三。

三、練習鞏固，融會貫通

教師設計了兩組檢測題，學生根據各自的學習基礎自主選擇，力求做到人人可檢測，個個有收獲。

A組

1.用長為20cm的鐵絲圍成兩個正方形，若其中一個邊長為xcm，設兩個正方形的面積之和S=f（x），則正確的是（ ）。

A.f（x）的定義域是[0，5]

B.f（x）=x2+（5-x）2（0＜x＜5）

2.要做一個底面為長方形的帶蓋的箱子，其體積為72cm3，底面兩鄰邊邊長之比為1：2，則它的長為_____，寬為_____，高為_____時，表面積最小。

B組

1.把長為100cm的鐵絲分成兩段，圍成一個正方形與一個圓，那么怎樣分，能使它們的面積之和最小？

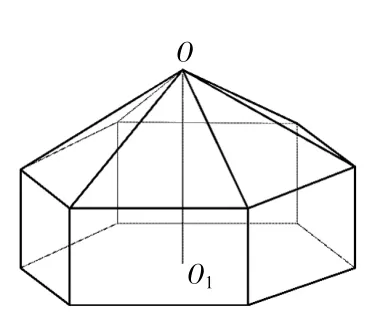
2.請同學們設計一個帳篷。它下部的形狀是高為1m的正六棱柱，上部的形狀是側棱長為3m的正六棱錐（如右圖所示）。試問當帳篷的頂點O到底面中心O1的距離為多少時，帳篷的體積最大？

四、總結反思，提升經驗

學生談談對這節課的收獲，教師利用學生的反饋，引導學生進行總結反思，及時提升經驗。

（作者單位：長沙市第二十一中學）