一類四維超混沌系統(tǒng)全局指數(shù)吸引集的新結果

尹社會，張　勇

(河南工業(yè)職業(yè)技術學院基礎教學部，河南 南陽 473000)

一類四維超混沌系統(tǒng)全局指數(shù)吸引集的新結果

尹社會，張勇

(河南工業(yè)職業(yè)技術學院基礎教學部，河南 南陽 473000)

[摘要]基于微分方程的基本理論和方法，采用理論分析和計算機模擬相結合的方式，利用微分方程比較定理研究了一類四維超混沌系統(tǒng)的全局指數(shù)吸引集.對于系統(tǒng)的不同參數(shù)，得到了該超混沌系統(tǒng)全局吸引集統(tǒng)一的數(shù)學表達式，同時得到了正半軌線的速率估計.最后，用計算機模擬驗證了計算理論的正確性.該研究結果為超混沌系統(tǒng)的混沌控制、混沌同步、吸引子維數(shù)的估計提供了理論依據(jù).

[關鍵詞]超混沌系統(tǒng)；全局指數(shù)吸引集；混沌同步；計算機仿真

0引言

混沌理論可以追溯到1900年龐加萊關于三體問題的研究.混沌系統(tǒng)的發(fā)展大致可以分為4個階段[1]：第1階段從1900年至1974年，主要貢獻為三體問題、KAM理論、蝴蝶效應Lorenz混沌吸引子的發(fā)現(xiàn)、Henon映射的研究；第2階段從1975年至1989年，主要貢獻為Logistic人口模型的提出、混沌同步理論的提出、Chua電路的發(fā)現(xiàn)；第3階段從1990年至1999年，主要貢獻為混沌控制OGY方法的實現(xiàn)、混沌系統(tǒng)同步的實現(xiàn)、混沌保密通信的研究、混沌反控制的提出、Chen系統(tǒng)的提出；第4階段從2000年至今，隨著復雜網(wǎng)絡的進一步研究與發(fā)展，從而推動了混沌理論的發(fā)展，主要貢獻為復雜網(wǎng)絡同步的研究.

混沌系統(tǒng)有著對系統(tǒng)初值和系統(tǒng)參數(shù)的敏感依賴性.1963年，美國氣象學家Lorenz在研究大氣層的熱對流問題時發(fā)現(xiàn)了第1個混沌模型即Lorenz混沌系統(tǒng)；1999年，陳關榮等[2]提出了一類與Lorenz系統(tǒng)為對偶系統(tǒng)的Chen混沌系統(tǒng)；2002年，Lü等人[3]提出了一類處于Lorenz與Chen之間的過渡系統(tǒng)，即Lü混沌系統(tǒng)，同年Lü等人[4]提出了統(tǒng)一混沌系統(tǒng)模型；2007年，王興元[5]等提出了超混沌Lorenz系統(tǒng).人們不斷發(fā)現(xiàn)新的混沌系統(tǒng)，并且揭示新的動力學特性是動力系統(tǒng)的一個重要研究方向.混沌系統(tǒng)在數(shù)學、物理、化學、電路、混沌保密通信、圖像加密、控制理論、激光、神經(jīng)網(wǎng)絡等領域都有著非常重要的應用價值[6-24].本文研究了一類新超混沌系統(tǒng)的動力學行為，該結果將為超混沌系統(tǒng)的混沌控制、混沌同步、吸引子維數(shù)的估計提供理論依據(jù).

1動力系統(tǒng)模型及其主要結果

一類新超混沌系統(tǒng)的動力系統(tǒng)模型為[25]：

(1)

其中A，b，c，d，e，f，g，h均為系統(tǒng)(1)的正參數(shù).并且當A=35，b=4，c=25，d=5，e=35，f=100，g=1，h=1 時，系統(tǒng)(1)存在一個典型的超混沌吸引子[25].

當A=35，b=4，c=25，d=5，e=35，f=100，g=1，h=1時，系統(tǒng)(1)軌線相圖見圖1.

圖1　系統(tǒng)(1)軌線的相圖

定理對于任意的A>0，b>0，c>0，d>0，e>0，f>0，g>0，h>0，令：

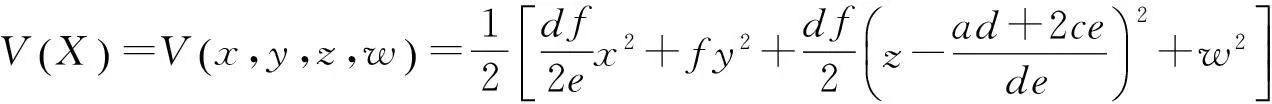
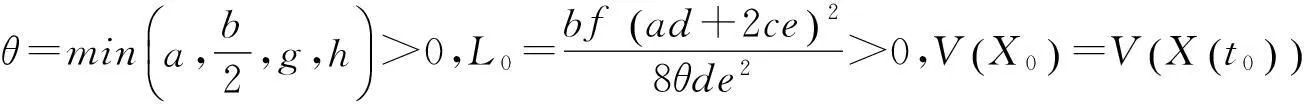
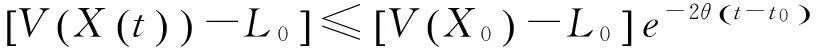
(2)

取上極限得

從而

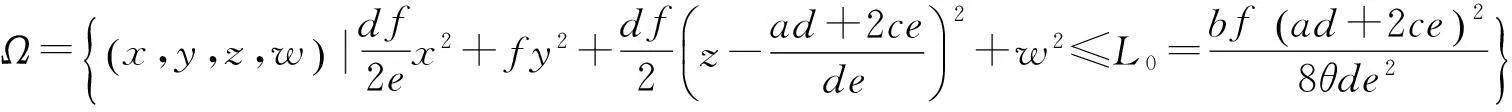
為系統(tǒng)(1)的一個全局指數(shù)吸引集.

證明定義

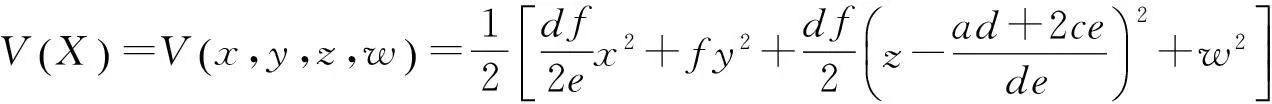
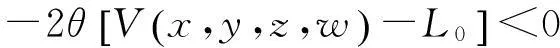
從而有

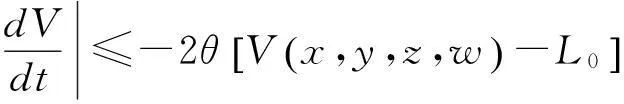
(3)

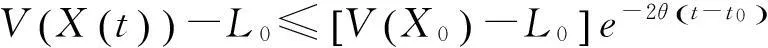
令t→+∞，取上極限得

從而

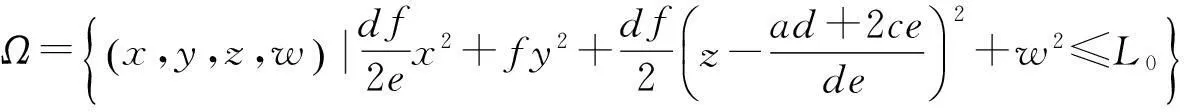
為系統(tǒng)(1)的一個全局指數(shù)吸引集.其中

說明：

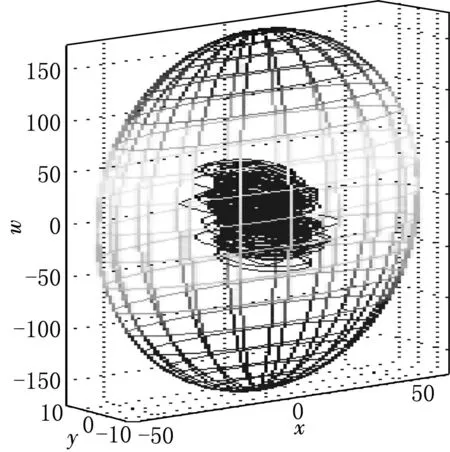
圖2　系統(tǒng)(1)的正半軌線最終進入橢球之內(nèi)

(1)本文得到系統(tǒng)(1)的最終界估計不僅比文獻[25]中的界估計結果更準確，而且給出了軌線的速率估計.

(2)取參數(shù)A=35，b=4，c=25，d=5，e=35，f=100，g=1，h=1，由定理可知系統(tǒng)(1)的一個全局指數(shù)吸引集為

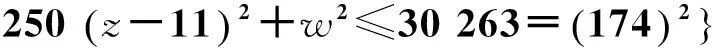
系統(tǒng)(1)的正半軌線在xyw相空間中的最終界估計見圖2.

2結論

本文基于微分方程的理論與方法研究了一類超混沌系統(tǒng)的全局指數(shù)吸引集，得到了其統(tǒng)一的數(shù)學表達式.該研究結果為系統(tǒng)電子振蕩電路的實現(xiàn)和通信工程設計等應用提供了理論依據(jù).

[參考文獻]

[1]閆振亞.復雜非線性波的構造性理論及其應用[M].北京：科學出版社，2002：15-17.

[2]CHEN G R，UETA T.Yet another chaotic attractor[J].International Journal of Bifurcation and Chaos，1999，9(7)：1465-1466.

[3]Lü J H，CHEN G R.A new chaotic attractor coined[J].International Journal of Bifurcation and chaos，2002，12(3)：659-661.

[4]Lü J，CHEN G，CHENG D，et al.Bridge the gap between the Lorenz system and the Chen system[J].International Journal of Bifurcation and Chaos，2002，12(12)：2917-2926.

[5]WANG XINGYUAN，WANG MINGJUN.A hyperchaos generated from Lorenz system[J].Physica A：Statistical Mechanics and Its Applications，2008，387(14)：3751-3758.

[6]汪威，朱曉剛，李俊杰，等.Feigenbaum 吸引子的動力性質(zhì)[J].東北師大學報(自然科學版)，2014，46(4)：48-51.

[7]梁春輝，張運波，孟祥萍，等.自適應反演控制在一類非線性系統(tǒng)中的應用[J].東北師大學報(自然科學版)，2014，46 (4)：66-71.

[8]汪威，李健，朱曉剛，等.一類代換系統(tǒng)及其超空間系統(tǒng)[J].東北師大學報(自然科學版)，2015，47(3)：9-11.

[9]SONG ZIGEN，ZHEN BIN，XU JIAN.Species coexistence and chaotic behavior induced by multiple delays in a food chain system[J].Ecological Complexity，2014，19：9-17.

[10]SONG ZIGEN，XU JIAN，LI QUNHONG.Local and global bifurcations in an SIRS epidemic model[J].Applied Mathematics and Computation，2009，214：534-547.

[11]SONG ZIGEN，XU JIAN.Stability switches and double Hopf bifurcation in a two-neural network system with multiple delays[J].Cognitive Neurodynamics，2013，7：505-521.

[12]SONG ZIGEN，XU JIAN.Stability switches and multi-stability coexistence in a delay-coupled neural oscillators system[J].Journal of Theoretical Biology，2012，313：98-114.

[13]WANG XINGYUAN，HE GUOXIANG.Cryptanalysis on a novel image encryption method based on total shuffling scheme[J].Optics Communications，2011，284(24)：5804-5807.

[14]趙國輝，舒永錄.一個新超混沌系統(tǒng)的控制與自適應同步[J].重慶工商大學學報(自然科學版)，2011，28(1)：1-7.

[15]何興，舒永錄，趙顯鋒.離散混沌系統(tǒng)的脈沖控制[J].重慶工商大學學報(自然科學版)， 2010，27(5)：431-434.

[16]張勇，付木亮.高維混沌模型的動力學分析及仿真[J].江西科學，2015，33(2)：160-161.

[17]袁紅，張付臣，李小武.關于 Hopf 分岔中向量函數(shù)泰勒公式中算子系數(shù)表示的評注[J].重慶工商大學學報(自然科學版)，2012，29(10)：6-10.

[18]湯志浩，張勇.幾類高維類 Lorenz 混沌模型的穩(wěn)定性分析及其仿真[J].江西科學，2015，33(4)：464-466.

[19]HE XING，YU JUNZHI，HUANG TINGWEN，et al.Neural networks for solving nash equilibrium problem in application of multiuser power control[J].Neural Networks，2014，57(9):73-78.

[20]HE XING，LI CHUANDONG，HUANG TINGWEN，et al.A recurrent neural network for solving bilevel linear programming problem[J].IEEE Transactions on Neural Networks and Learning Systems，2014，25(4)：824-830.

[21]LIU HONGJUN，WANG XINGYUAN.Color image encryption using spatial bit-level permutation and high-dimension chaotic system[J].Optics Communications，2011，284(16)：3895-3903.

[22]LEONOV G，KUZNETSOV N.Hidden attractors in dynamical systems.From hidden oscillations in Hilbert-Kolmogorov，Aizerman，and Kalman problems to hidden chaotic attractor in Chua circuits[J].International Journal of Bifurcation and Chaos，2013，23：1330002-1-1330002-69.

[23]ZHANG FUCHEN，SHU YONGLU，YANG HONGLIANG.Bounds for a new chaotic system and its application in chaos synchronization[J].Communications in Nonlinear Science and Numerical Simulation，2011，16(3)：1501-1508.

[24]ZHANG FUCHEN，SHU YONGLU，YANG HONGLIANG，et al.Estimating the ultimate bound and positively invariant set for a synchronous motor and its application in chaos synchronization[J].Chaos，Solitons & Fractals，2011，44(1)：137-144.

[25]張曉丹，崔麗娟.一類四維超混沌系統(tǒng)的界及同步的研究[J].物理學報，2011，60 (11)：1-7.

(責任編輯：石紹慶)

New results of globally exponentially attractive set for a class of hyperchaotic systems

YIN She-hui，ZHANG Yong

(Department of Basic Teaching，Henan Polytechnic Institute，Nanyang 473000，China)

Abstract:Based on the theory and the method of differential equations，this paper investigates complex dynamical behaviors of a new class of hyper-chaotic systems by theoretical analysis and matlab simulation combined method.The global attractive sets of this hyperchaotic system are obtained.In this paper，the unified mathematical expression of the global attractive sets of the system are obtained by the comparison theorem of differential equations.Finally，computer simulation verifies the correctness of the theoretical calculation.This article provides a theoretical basis for chaos control，chaos synchronization，the attractor dimension estimate of this system.This method can be extended to study other chaotic systems.

Keywords:hyperchaotic system；globally exponentially attractive set；chaos synchronization；computer simulation

[文章編號]1000-1832(2016)02-0052-04

[收稿日期]2013-12-14

[基金項目]河南省基礎與前沿技術項目(142300410416)；南陽市科學技術發(fā)展規(guī)劃項目(2012GG035).

[作者簡介]尹社會(1979—)，男，碩士，講師，主要從事物理、混沌控制等研究；通訊作者：張勇(1981—)，男，碩士，講師，主要從事數(shù)學理論研究.

[中圖分類號]O 241.84；O 29；O 242.1[學科代碼]110·61

[文獻標志碼]A

[DOI]10.16163/j.cnki.22-1123/n.2016.02.013