歐拉方程組徑向對稱正規解的爆破

朱旭生，湯傳揚，王　莉

(華東交通大學理學院，江西 南昌 330013)

歐拉方程組徑向對稱正規解的爆破

朱旭生，湯傳揚，王莉

(華東交通大學理學院，江西 南昌 330013)

[摘要]研究了N維可壓縮歐拉方程組真空問題徑向對稱正規解的爆破問題，利用積分法得出該問題非平凡徑向對稱正規解(ρ，v)在有限時間內發生爆破.

[關鍵詞]歐拉方程組；徑向對稱；正規解；積分法；爆破

1預備知識

本文考慮N維可壓縮歐拉方程組

(1)

在滿足初始條件

(2)

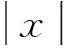
(ⅰ)(ρ，u)(x，t)∈C1(Rn×[0，T))；

(ⅱ)P(ρ)(x，t)∈C1(Rn×[0，T))；

(ⅲ)在ρ的緊支集之外，u滿足

(3)

關于歐拉方程經典解的爆破問題在一些文獻中已有討論：文獻[1-2]討論初值問題解的爆破；文獻[3-6]討論了真空情形經典解的爆破，其中文獻[3-5]討論了正規解的爆破，文獻[6]利用平面自治系統定性理論研究了徑向對稱(有時也稱軸對稱或球對稱)解的爆破；文獻[7-12]討論了真空情況下歐拉方程組或帶排斥力的歐拉泊松方程徑向對稱解的爆破問題.這些文獻研究的大多是初值問題，只有文獻[6，13]研究的是初邊值問題.

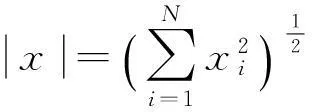
(4)

將(4)式代入(1)式中得

(5)

其相應的初始條件為

(6)

相應地，當0≤r0；當r≥R1時，ρ0(r)=0.對初值v0(r)，我們假設當r≥R2時v0(r)=0，這里R2≥R1.對于徑向對稱的歐拉方程組的正規解，除滿足(ρ，u)(x，t)∈C1(Rn×[0，T))外，在ρ的緊支集外(4)式變為

vt+VVr=0.

(7)

當然，為了去掉在x=0處的奇性，要求v(0，t)=0，vr(r，t)=o(r).

2主要結論及證明

定理1設(ρ，v)是N維歐拉方程組初值問題(1)—(2)在真空條件下的非平凡經典解，即做徑向變換后(5)—(6)的經典解.假設suppρ0?{r|r≤R2}，當r≥R2時v0(r)=0，且

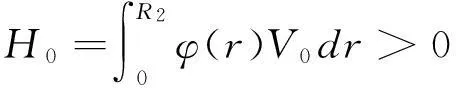
(8)

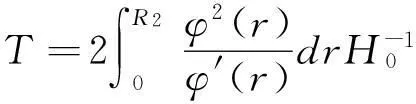
證明首先處理真空邊界.設suppρ(r，t)={r|r≤R1(t)}，由于函數v∈C1，故由(7)式可知R1(t)滿足

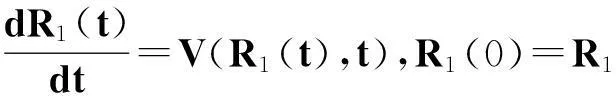
(9)

將上式兩端關于t求導，并由(7)式得

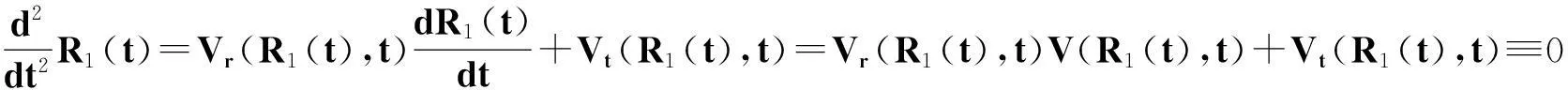
從而

R1(t)=R1(0)+v(R1(0)，0)t=R1+v0(R1)t.

(10)

其次，引入隨體導數

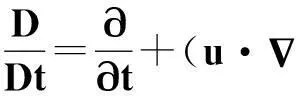
(11)

利用(11)式可以將(1)式第一個方程改寫為

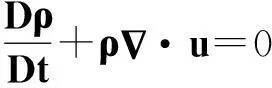
(12)

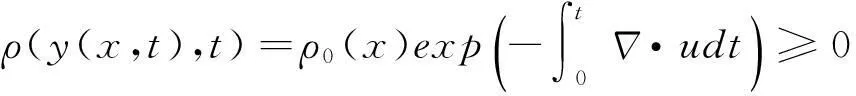
(13)

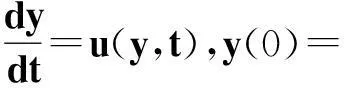
下面處理速度為零的邊界點.由于點R2也落在suppρ0外，故此處也滿足(7)式，從而

同樣解得

R2(t)=R2+v0(R2(0))t=R2.

(14)

將壓強函數P=P(ρ)=Kργ代入(6)式第二個方程得

ρ(vt+VVr)+Kγργ-1ρr=0.

(15)

當0≤r0，故

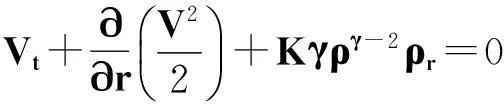
(16)

由于γ>1，故ργ-1(r，t)∈C([0，+∞)×[0，T))，且當rR1(t)時，ργ-1∈C1.當1<γ<2時，ργ-1在r=R1(t)處關于r不可導，但?r(ργ-1)在r=R1(t)處具有可積的奇性，因此在做積分時我們可以認為(16)式對任意區域均成立.

引入函數φ(r)≥0，φ(r)∈C1([0，R2))，φ′(r)>0.將(16)式兩端同乘以φ(r)，

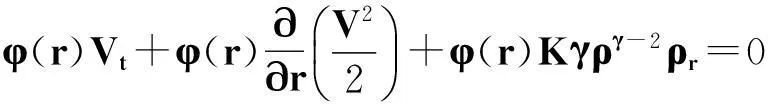
(17)

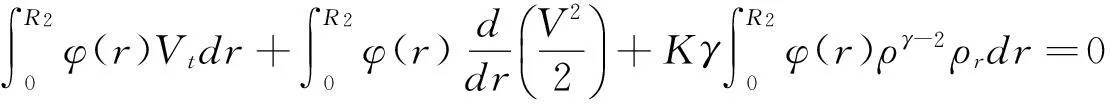
(18)

即

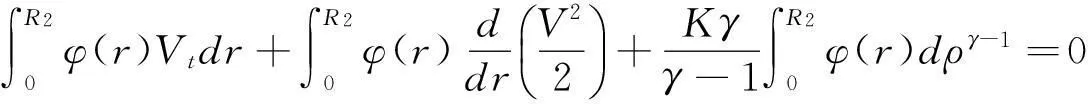
(19)

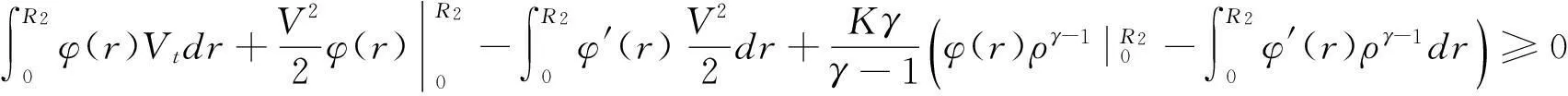
(20)

利用v(R2，t)=ρ(R2，t)=0，(20)式可改寫為

(21)

這里因為φ′(r)>0，K≥0且γ>1，從而

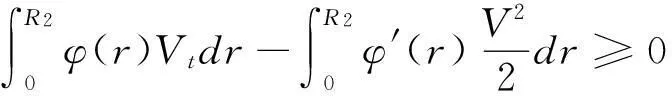
(22)

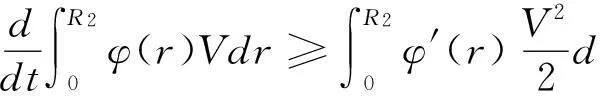
(23)

令

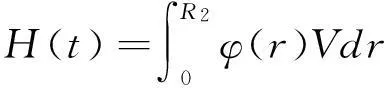
(24)

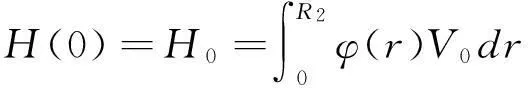
則(23)式化簡為

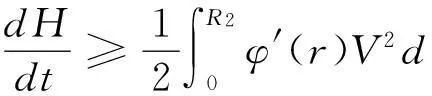
(25)

進一步由Cauchy-Schwarz不等式得

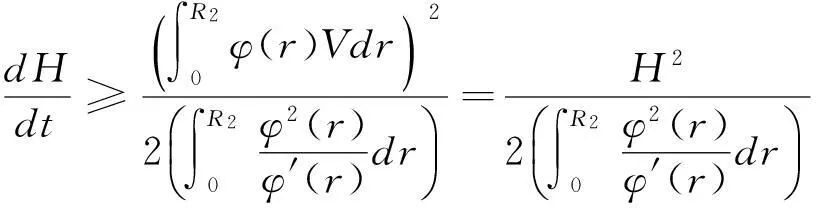
(26)

令

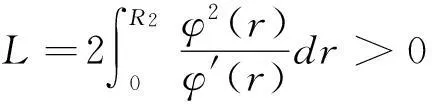
(27)

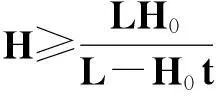
(28)

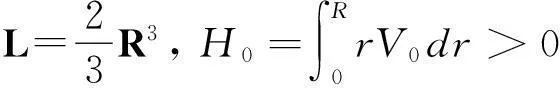
注2如果R1=R2=R，我們的結論與文獻[12]中當R(t)=R時的結論一致.

[參考文獻]

[1]ALINHAC S.Blowup for nonlinear hyperbolic equations[M].Boston：Birkhauser，1995:33-36.

[2]SIDERIS T.Formation of singularities in three-dimensional compressible fluids[J].Comm Math Phys，1985，101：475-485.

[3]LIU T P，YANG T.Compressible Euler equations with vacuum[J].J Differential Equations，1997，140:223-237.

[4]MAKINO T，UKAI S，KAWASHIMA S.Sur la solution à support compact de l’équation d’Euler compressible[J].Japan J Indust Appl Math，1986(3)：249-257.

[5]ZHU XUSHENG，WANG WEIKE.The regular solutions of the isentropic Euler equations with degenerate linear damping[J].Chinese Ann Math B，2005，26(4)：583-598.

[6]LI T，WANG D.Blowup phenomena of solutions to the Euler equations for compressible fluid flow[J].J Differential Equations，2006，221：91-101.

[7]ZHU XUSHENG，TU AIHUA.Blowup of the axis-symmetric solutions for the IBVP of the isentropic Euler equations[J].Nonlinear Analysis：Theory，Methods & Applications，2014，95:99-106.

[8]YUEN M W.Blowup for the Euler and Euler-Poisson equations with repulsive force[J].Nonlinear Analysis Series A：Theory，Methods & Applications，2011，74:1465-1470.

[9]PERTHAME B.Nonexistence of global solutions to Euler-Possion equations for repulsive force[J].Japan J Appl Math，1990，7(2):363-367.

[10]MAKINO T.Blowing up solutions of the Euler-Poisson equations for the evolution of the gaseous stars[J].Transport Theory and Statistical Physics，1992，21:615-624.

[11]DENG Y B，XIANG J L，YANG T.Blowup phenomena of solutions to Euler-Poisson equations[J].J Math Anal Appl，2003，286:295-306.

[6]CHAE D H，TADMOR E.On the finite time blow-up of the Euler-Poisson equations of in RN[J].Commun Math Sci，2008，6:785-789.

[12]LI RUI，LIN XING，MA ZONGWEI，et al.Improved blow-up results for the Euler and Euler-Poisson equations with repulsive forces[J].J Math Anal Appl，2014，417：57-64.

[13]朱旭生，陳家樂，湯傳揚.可壓縮等熵歐拉方程組外問題的爆破[J].華東交通大學學報，2014(3)：105-109.

[14]胡衛敏，伊磊，陳維.一類分數階微分方程三點邊值問題的多重正解[J].東北師大學報(自然科學版)，2011，43(2):16-22.

[15]欒姝，徐鵬.一類串聯系統的邊界Carleman估計[J].東北師大學報(自然科學版)，2011，43(2):39-45.

(責任編輯：李亞軍)

Blowup of the radial symmetric regular solution for the Euler equations

ZHU Xu-sheng，TANG Chuan-yang，WANG Li

(School of Science，East China Jiaotong University，Nanchang 330013，China)

Abstract:The blowup of the radial symmetric regular solutions for the N-dim compressible Euler equations is studied，while the initial flow is vacuum outside a ball.Under some assumptions，it is shown that the non-trivial classical solutions (ρ，V)blowup on or before the finite time .

Keywords:Euler equations；radial symmetry；regular solution；integration method；blowup

[文章編號]1000-1832(2016)02-0031-04

[收稿日期]2014-10-15

[基金項目]國家自然科學基金資助項目(11161021，61262031，11326139);江西省科技廳項目(20142BAB211010).

[作者簡介]朱旭生(1968—)，男，副教授，主要從事偏微分方程研究；湯傳揚(1989—)，男，碩士，主要從事偏微分方程研究.

[中圖分類號]O 175.27[學科代碼]110·4720

[文獻標志碼]A

[DOI]10.16163/j.cnki.22-1123/n.2016.02.008