利用極化敏感陣列特性的信源數估計技術研究

吳娜，司偉建，焦淑紅，吳迪(哈爾濱工程大學 信息與通信工程學院，黑龍江 哈爾濱，150001)

?

利用極化敏感陣列特性的信源數估計技術研究

吳娜，司偉建，焦淑紅，吳迪
(哈爾濱工程大學 信息與通信工程學院，黑龍江 哈爾濱，150001)

摘要：針對極化敏感陣列多參數聯合估計中的信源數估計問題，提出一種基于去特征處理的信源數估計方法。首先，對極化敏感陣列接收數據矢量的協方差矩陣進行特征分解，得到的特征值的個數為陣元數的2倍，將求得的特征值降序排列，其中后半部分小特征值對應的特征矢量張成的子空間包含于噪聲子空間，利用這一特點構造投影矩陣；其次，通過去特征處理，重構新的協方差矩陣，求這些新協方差矩陣在投影矩陣上的投影；最后，根據投影結果構造判決函數，估計信源數。研究結果表明：入射角間隔和極化狀態角間隔對算法估計性能有影響。通過與蓋氏圓盤法的對比實驗驗證算法的有效性。

關鍵詞：極化敏感陣列；去特征處理；投影矩陣；信源數估計

極化敏感陣列是將極化敏感陣元在空間中按照一定的擺放形式所構成的陣列，利用極化敏感陣元可以獲取電磁波的極化信息，極化信息表現為極化敏感陣元的正交通道之間的相關特性，而空域信息表現為相鄰陣元之間的空間相位延遲，因此，可以利用極化敏感陣列的空間擺放形式獲取空域信息。極化敏感陣列為信號空間到達角和極化狀態的聯合估計創造了條件。自 20 世紀 90年代開始，一些研究者在空間譜估計的基礎上分別針對最大熵算法、MUSIC 算法、ESPRIT 算法等傳統波達方向估計方法在極化敏感陣列上的拓廣應用、極化敏感陣列解相干多參數估計以及減少極化敏感陣列多參數估計計算量等問題進行了研究，如：LI等[1?4]利用ESPRIT算法研究了不同情況下極化敏感陣列多參數估計問題；HURTADO 等[5]提出了利用極化分解圓環陣列天線估計多個共信道窄帶信號的空間二維到達角估計問題，比較了不同方法拓廣應用到極化分極陣列估計問題時的信號分辨特性和方位角估計精度，結果表明最大熵算法不能被拓廣應用，而MUSIC算法具有更好的綜合性能；LIU等[6?7]設計了Pencil-MUSIC算法，實現了解相干聯合估計；PAULUS等[8]利用Root-music算法探討了L型極化敏感陣列的二維到達角估計問題。以上極化敏感陣列多參數估計方法的實現均以已知入射信源個數為前提。而在實際應用中，信源數往往是未知參量，因此，在對多參數聯合估計之前，正確的信源數估計至關重要。現有的信源數估計方法均是將針對普通陣列的信源數估計方法直接推廣應用到極化敏感陣列的估計中。如性能較好的典型信源數估計方法有基于信息論準則的AIC 準則和 MDL 準則、正則相關技術和蓋氏圓方法(GDE)等[9?10]。其中，基于信息論準則的 AIC 準則和MDL準則只能適用于白噪聲背景，而實際應用時，一般為色噪聲背景，從而此方法無法應用[11]。正則相關技術需要 2個空間分離的陣列，這將在極化敏感陣列通道加倍的基礎上進一步增大硬件系統的開銷，在實際應用中難以實現。GDE方法運算量小，但估計精度有待提高。更重要的是，以上信源數估計方法并沒有利用極化敏感陣列自身的性質。為此，本文作者利用極化敏感陣列接收的數據性質，提出一種基于去特征處理的信源數估計算法。根據去特征處理構造新協方差矩陣，并求其在投影矩陣上的投影，根據投影結果設定判斷函數，區分對應信號子空間和噪聲子空間的新協方差矩陣個數，進而估計信源數。本文的特征分解運算與空間到達角和極化狀態量估計時的相同，分解結果可以直接應用于后續的聯合估計，減少了整體的計算量。通過計算機仿真實驗驗證所提出算法的有效性。

1　極化敏感陣列信號模型

文獻[12]提出了由極化敏感陣元組成的一維均勻線陣模型。設均勻線陣由N個極化敏感陣元構成，極化敏感陣元是由沿X軸方向和沿Y軸方向的2個偶極子構成的正交偶極子對，d 為陣元間距，θ為入射角度，如圖1所示。

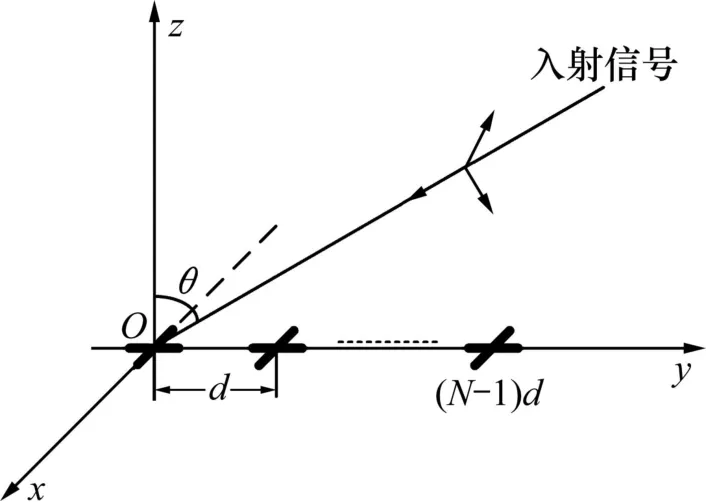
圖1　極化敏感陣列結構圖Fig.1　Structure of polarization sensitive array

為了分析方便且不失一般性，將所有入射信號的到達方向限制在YOZ平面，極化狀態限制在Poincare球面η=90°的大圓軌道上，即所有入射信號滿足η=90°，則可得到一維極化敏感均勻線陣的陣列導向矢量為

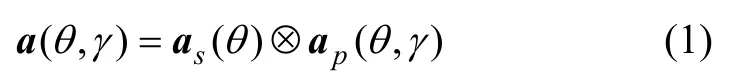
式中：“ ?”表 示Kronecker積；極 化導向矢量 ap(θ,γ)=[a(θ,γ)a (θ,γ)]T=[?Cos(γ)jcos(θ)sin(γ)]T；pxpy apx(θ,γ)和 apy(θ,γ)分別為極化導向矢量 ap(θ,γ)的2個正交分量；as(θ)為空域導向矢量，

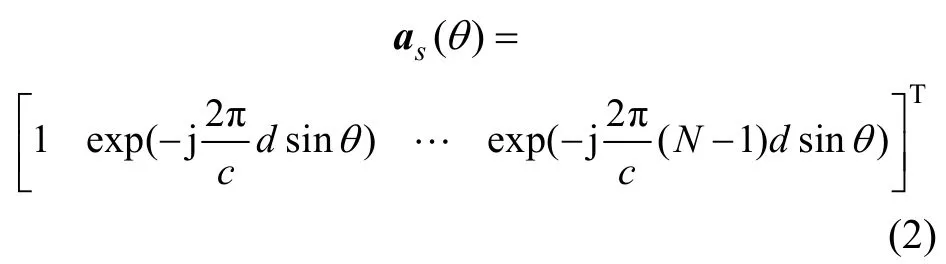
c 為電磁波傳播速度；f 為入射信號頻率。設有 K(K≤N)個信號入射到均勻線陣上，則陣列接收參數為

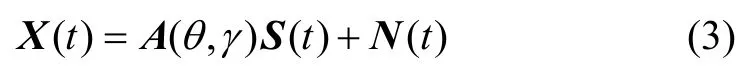
式中：X(t)=[ x1(t)x2(t)L x2N(t)]T，為陣列接收數據矢量；S(t)=[ s1(t)s2(t)L sK(t)]T，為信號矢量；N (t)=[ n1(t)n2(t)L n2N(t)]T，為 噪聲矢量；A(θ,γ)=[ a (θ1,γ1)a(θ2,γ2)L a (θK,γK)]，為 陣列導向矩陣。

極化敏感陣列可以看作由2個均勻線陣構成，這2個子陣分別是沿X軸和沿Y軸的N個偶極子構成的均勻線陣，其中，沿X軸的N個偶極子構成的均勻線陣定義為子陣 Xx，沿 Y 軸的 N 個偶極子構成的均勻線陣定義為子陣 Xy。將陣列接收數據矢量的奇數位

取出，可以得到子陣 Xx的數據矢量為

同理，將陣列接收數據矢量的偶數位取出，得到子陣 Xy的數據矢量為

將陣列接收數據矢量重新排列，得到新的陣列接收數據矢量為

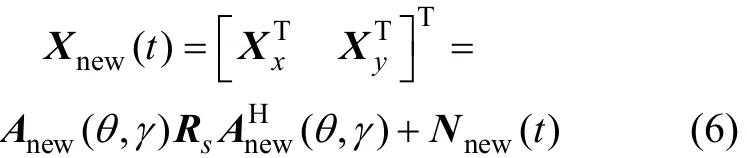
其中：Nnew(t)=[n1(t)Ln2n?1(t)n2(t)L n2n(t)]T；Anew(θ,γ)為新陣列接收數據矢量對應的陣列流型矩陣，

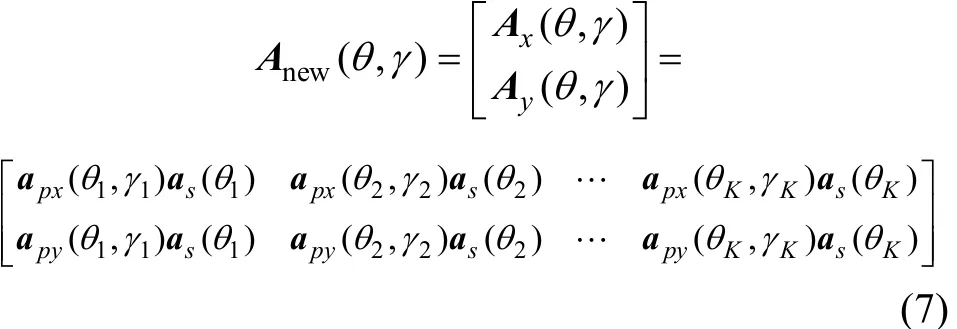
設陣列接收的噪聲為零均值加性空間平穩高斯白噪聲，噪聲功率為2σ，則數據協方差矩陣為

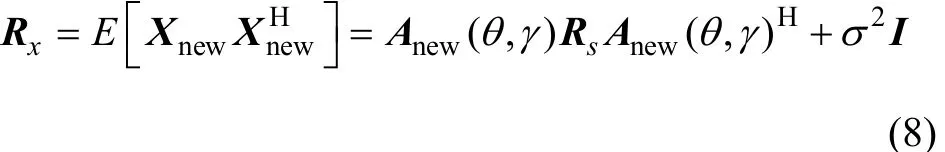
對其進行特征分解得

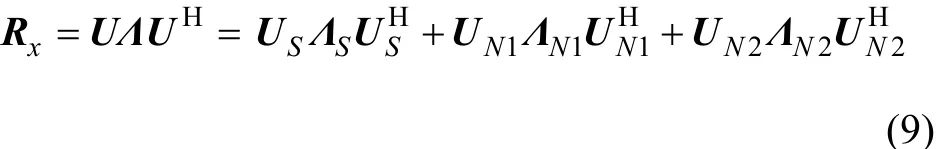
式中：Λ=diag {λ1λ2L λ2N}，滿 足 λ1≥ λ2≥L ≥ λK>λK+1=L=λN=L=λ2N；前K個大特征值對應的特征矢量構成了信號子空間 US=[u1u2L uK]，UN1=[uK+1uK+2L uN]是由第 K 個到第 N 個特征值對應的特征矢量構成的矩陣，張成的空間包含于噪聲子空間，UN2=[ uN+1uN+2L u2N]是由后 N 個小特征值對應的特征矢量構成的矩陣，張成的空間同樣包含于噪聲子空間。

將陣列導向矢量陣按行分塊可以得到 Anew的另一種表示形式：

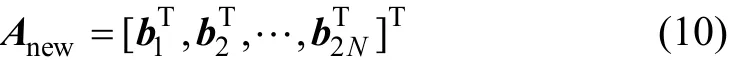
其中：“T”表示矩陣轉置；bi為 Anew的第 i 行元素構成的行向量，具體形式為

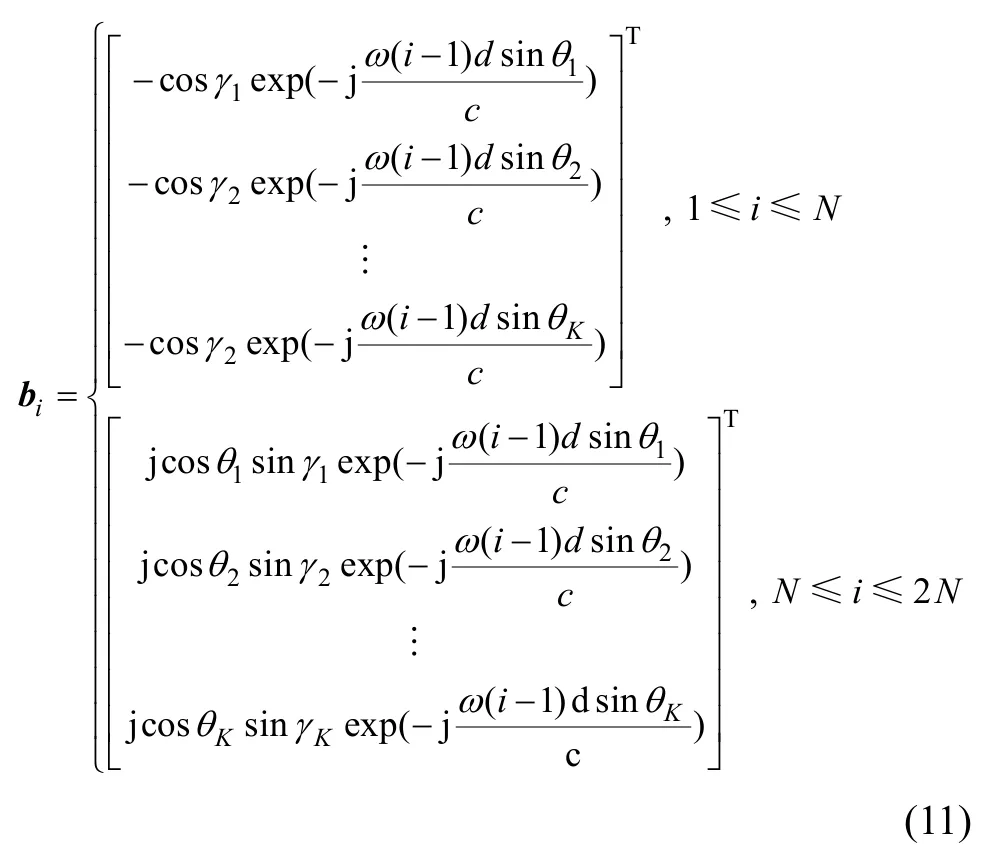
則陣列輸出的數據協方差矩陣可以表示為

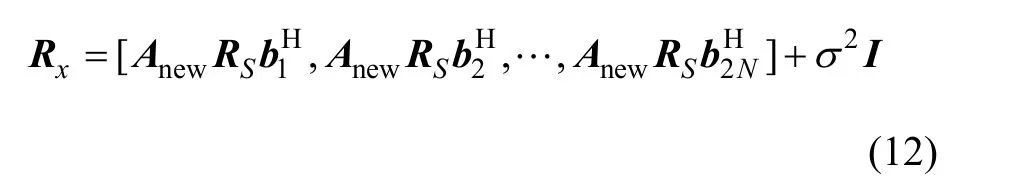
已知各信號源相互獨立，則 RS為滿秩對角陣，因此，有成立。

2　去特征處理信源數估計算法

用數據協方差矩陣 Rx的前 N 個特征值分別對其進行去特征處理，得到N個新協方差矩陣 R′ xi ：

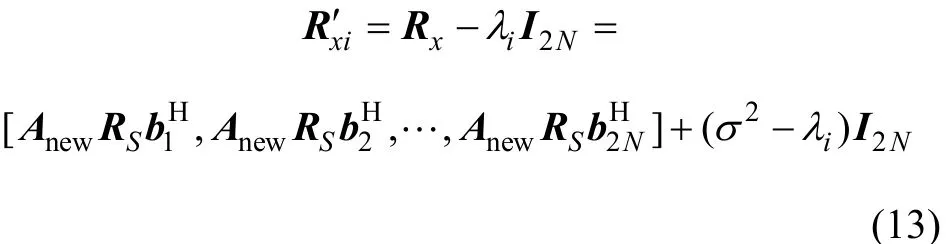
式中：i=1,2,…,N；λi為將數據協方差矩陣的特征值進行降序排列后的第i個特征值；I2N為2N ×2N 維單位矩陣。

取(9)式中的 UN 2為投影矩陣，分別求在 UN 2上的投影，得

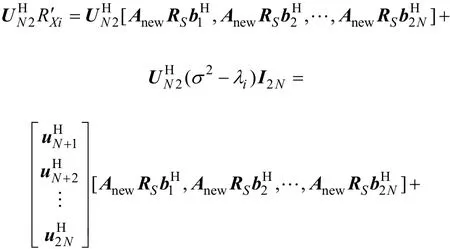
式中：ei(i=1,2,L,2N)為單位矩陣 I2N的第i列。易知ui(N≤ i≤2 N)∈ span(UN 2)? span(UN)，且有span(UN)⊥ Anew成立，因此，

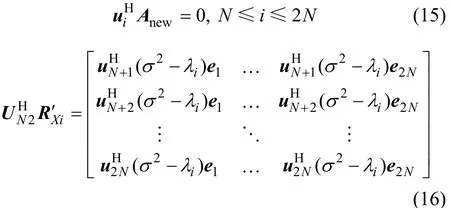
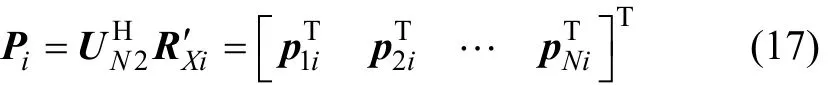
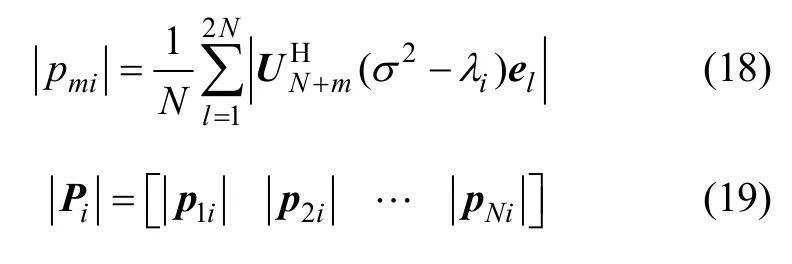
1)當1≤i≤K時，λi為對應于信號子空間的特征值，λi＞＞ σ2，則是1個取值較大的數，對應的為1個每個元素都為較大值的向量。

2)當K+1≤i≤N時，λi為對應于噪聲子空間的特征值，λi=σ2，則取值為 0，在實際情況中是1個較小值，對應的為1個每個元素都為較小值的向量。

定義 ∑ P 為對向量P的所有元素求和，構 造判據函數如下：

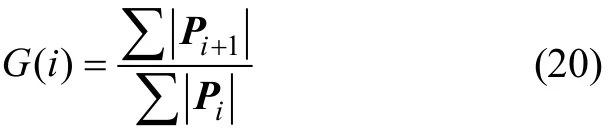
3　算法步驟

根據前面理論分析，本文算法的實現步驟如下。步驟1：根據式(8)估計協方差矩陣 Rx。

步驟2：對協方差矩陣 Rx進行特征值分解。

步驟3：用 Rx的前N個特征值分別對其進行去特征處理，得到N個新協方差矩陣。

步驟4：利用 Rx的后N個小特征值對應特征向量構造投影矩陣 UN 2。

步驟6：根據式(20)中的判據函數求得信源數。

其中步驟3和步驟4 可以并行進行。需要說明的是：本文在理論推導過程中假設陣列接收噪聲為空間白噪聲，若空間噪聲為色噪聲，則噪聲功率不為1個固定值，在信噪比大于一定值后，仍滿足噪聲功率遠小于對應信號的特征值這一特點，因此，本文算法在陣列接收噪聲為色噪聲情況下仍適用。

4　計算復雜度分析

本文算法的計算量主要集中在協方差矩陣的構造、特征值分解及投影運算上。由2N ×1維向量構造協方差矩陣的計算量為C1= 4N2，構造的協方差矩陣維數為2N ×2N，對該2N ×2N 維矩陣進行特征分解，采用文獻[13]中的快速子空間分解技術可將計算量降低至C2=2N(L+2)2。求在特征空間 U 上的投影矩陣的計算量為C31= 4N3，算法共有 N 次該投影運算，則求投影矩陣運算的計算量為C=NC=4N4，本文算法 的 總計算量為331C=C+C+C=4N2+2N(L+2)2+4N4。而經典算法大多僅需要進行協方差矩陣構造和協方差矩陣特征分解，本 文算法的投影矩陣運算引入了一定的計算量，導致最終算法的復雜度增加，但該算法在2種噪聲背景下及白噪聲和空域相關色噪聲并存背景下估計性能提高。

5 仿真實驗分析

下面通過計算機仿真對算法的性能進行分析。設極化敏感陣列為 8元均勻線陣，極化敏感陣元為正交偶極子，陣元間距為入射信號波長的一半，快拍數為200，每個實驗均進行200次獨立重復實驗。成功檢測概率指 200次獨立重復實驗中正確測得信源數的實驗次數與總實驗次數的比值。

實驗1：入射角間隔和極化狀態角間隔對成功檢測概率的影響。

與普通陣列信號處理不同，在極化敏感陣列參數估計問題中，需要同時考慮入射角間隔和極化狀態角間隔對算法性能的影響。為 了直觀地觀測到這一影響，設計本實驗。仿真條件如下：2 個遠場窄帶信號入射到8元均勻線陣上，取信噪比為10 dB。固定 θ1=5°，γ1=5°，設入射角間隔 ?θ以 0.5°為步長從 0°變化到6°，θ2=θ1+?θ，極化狀態角間隔?γ以1°為步長從0°變化到 36°，γ2=γ1+?γ。通過計算機仿真得到本文算法的成功檢測概率與入射角間隔及極化狀態角間隔之間的關系，如圖2所示。

圖 2(a)所示為成功檢測概率與方位角間隔和極化狀態角間隔之間關系的三維圖，圖 2(b)所示為對應圖2(a)的等高線圖，曲線的顏色對應極化狀態角和方位角取值的成功概率，2(a)和2(b)中最下邊的曲線及其與坐標軸圍成的下半范圍上的點的成功概率均為 0，從下到上的曲線成功概率依次變大；最上邊曲線及其與坐標軸圍成的上半范圍上的點成功概率則均為1。從圖 2(a)和圖 2(b)可以看出：本文算法的成功檢測概率隨2種角度間隔變大而變大。這 是由于角度間隔變大，信號間的相互干擾變小，成功檢測概率變大；當方位角間隔大于 5°、極化狀態角間隔大于 33°時，本文算法可以以概率1成功估計出信源數。同 時還可以看出：當極化狀態角間隔為0°時，入 射角間隔大于5°時的成功檢測概率為100%；而當入射角間隔為 0°時，極化狀態角間隔大于33°時的成功檢測概率為100%，這說明入射角對算法性能的影響要比極化狀態角對算法性能的影響更明顯，即極化敏感陣列不僅可以在空域將電磁信號區分開來，而且可以利用極化信息提高系統的分辨力。

實驗2：信噪比對成功檢測概率的影響。

為了驗證信噪比對本文算法的影響及色噪聲背景下算法的魯棒性，設計本實驗。仿真條件如下：3 個遠場窄帶信號入射到該均勻線陣上，入射角度分別為θ=[15°25°35°]，極化狀態角分別為γ=[20°30°40°]。圖3和圖4所示分別為白噪聲和色噪聲背景下本文算法與 GDE 算法估計信源數的成功檢測概率隨信噪比的變化規律。

從圖3 和圖4可以看出：這2 種算法的信源數估計成功檢測概率均隨信噪比變大而變大，而本文算法在2種噪聲背景下的成功檢測概率均比傳統 GDE 算法的高；在白噪聲背景下，本文算法在信噪比為6 dB時成功檢測概率可達100%，而GDE算法信噪比需要達到12 dB以上才能實現100%成功檢測；在 色噪聲背景下，本 文算法在信噪比為8 dB時成功檢測概率可以達到100%，而GDE算法信噪比仍然需要達到12 dB以上才能實現100%成功檢測。由此可見本文算法的估計性能明顯優于 GDE 算法。對比圖3和圖4還可以看出：這2種算法在白噪聲背景下的估計性能優于在色噪聲背景下的估計性能。

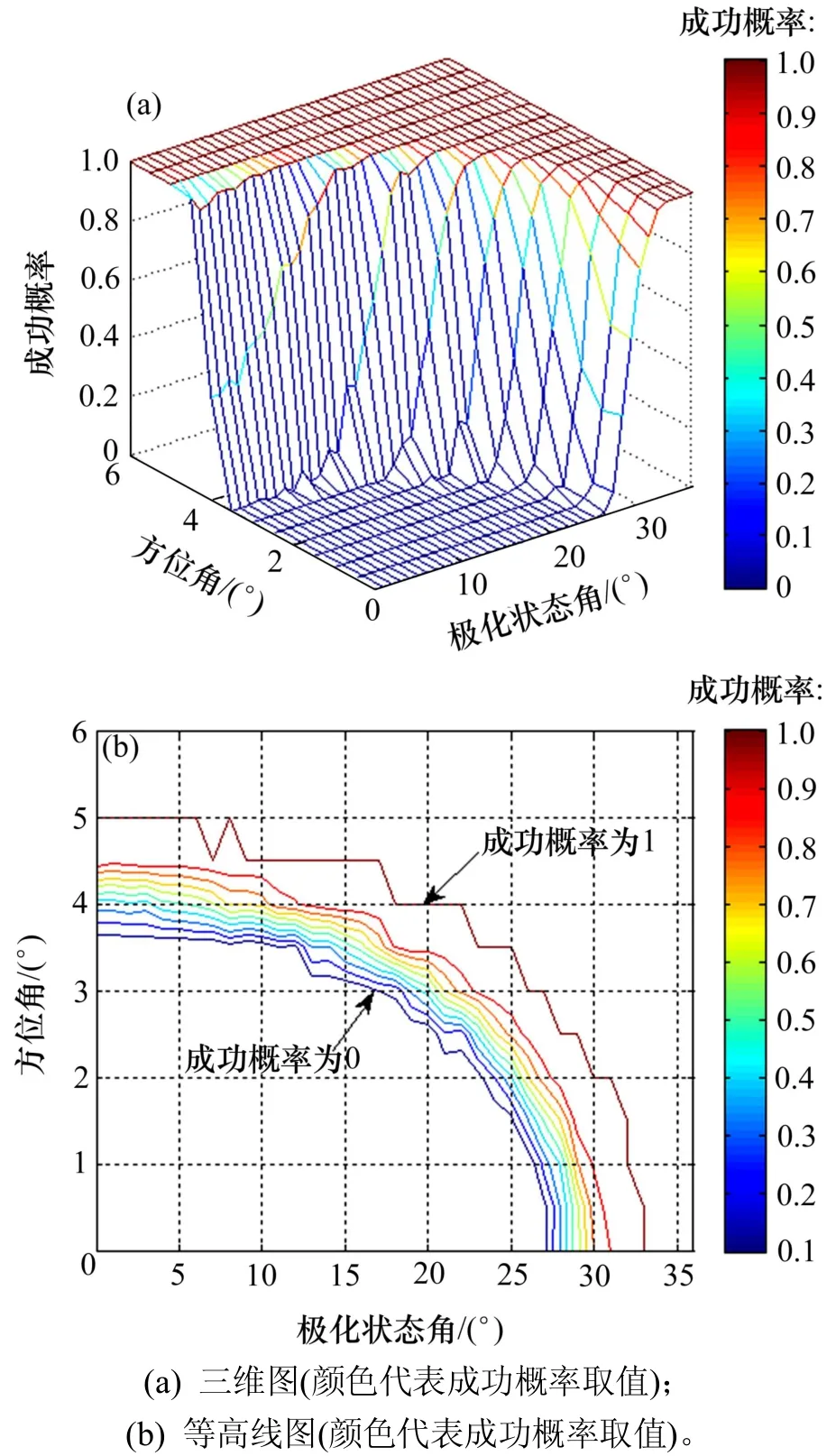
圖2成功檢測概率與方位角間隔及極化狀態角間隔的關系Fig.2Relationship among probability of success result,azimuth angle intervals and polarization state angle intervals

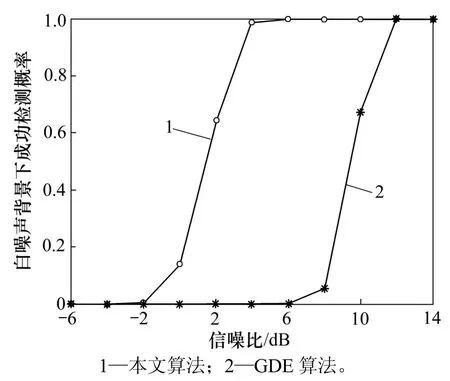
圖3　白噪聲背景下成功檢測概率與信噪比的關系Fig.3　Relationship between probability of success and SNR in white noise

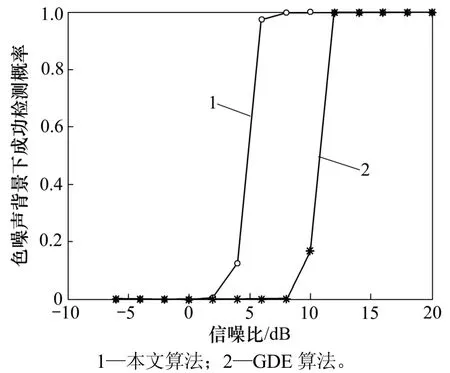
圖4色噪聲背景下成功檢測概率與信噪比的關系Fig.4Relationship between probability of success and SNR inColor noise

6 結論

1)針對極化敏感陣列信源數估計問題，提出了一種適用于極化敏感陣列的去特征處理信源數估計算法。對極化敏感陣列接收數據構造的協方差矩陣進行特征值分解求得的較小特征值包含于噪聲子空間中，算法利用了極化敏感陣列這一特點構造投影矩陣，并對經過去特征處理獲得的新協方差矩陣求投影，進而構造判決函數，求得信源數。

2)這種算法的估計性能優越，算法中特征分解的結果可以直接應用于后續的子空間類DOA估計算法，從總體上減少了計算量。對比實驗結果驗證了該算法的有效性。

參考文獻：

[1]EL K M N,BOYER R,RENAUX A,et al.Statistical resolution limit of the uniform linearCo-centered orthogonal loop and dipole array[J].Signal Processing,IEEE Transactions on,2011,59(1): 425?431.

[2]JIANG Hong,WANG Defa,LIUChang.Joint parameter estimation of DOD/DOA/polarization for bistatic MIMO radar[J].The Journal ofChina Universities of Posts and Telecommunications,2010,17(5): 32?37.

[3]YUAN Xin,Wong K T,Agrawal K.Polarization estimation with a dipole-dipole pair,a dipole-loop pair,or a loop-loop pair of various orientations[J].Antennas and Propagation,IEEE Transactions on,2012,60(5): 2442?2452.

[4]LI J,JRCOMPTON R T.Angle and polarization estimation using ESPRIT with a polarization sensitive array[J].IEEE Transactions on Antennas and Propagation,1991,39:1376?1383.

[5]HURTADO M,XIAO Jinjun,NEHORAI A.Target estimation,detection,and tracking[J].Signal Processing Magazine,IEEE,2009,26(1): 42?52.

[6]LIU Jun,LIU Zheng,LIU Qin.Direction and polarization estimation forCoherent sources using vector sensors[J].Journal of Systems Engineering and Electronics,2013,24(4): 600?605.

[7]WANG Liguo,WANG Fei.A joint estimation method of azimuth,elevation,range and polarization for near field sources based on second order statistics[C]//Computer Science and Network Technology(ICCSNT),2011InternationalConference on.IEEE,2011: 771?775.

[8]PAULUSC,MARS J I.Vector-sensor array processing for polarization parameters and DOA estimation[J].EURASIP Journal on Advances in Signal Processing,2010: 61.

[9]LU Zhihua,Abdelhak M.Zoubir.Generalized Bayesian informationCriterion for source enumeration in array processing[J].IEEE Trans on Signal Processing,2013,61(6):1470?1480.

[10]葉中付,向利,徐旭.基于信息論準則的信源個數估計算法改進[J].電波科學學報,2007,22(4): 593?598.YE Zhongfu,XIANG Li,XU Xu.Improvement of source number estimation based on information theoreticCriteria[J].Chinese Journal of Radio Science,2007,22(4): 593?598.

[11]司偉建,林晴晴.基于特征子空間投影的信源數估計方法[J].系統工程與電子技術,2012,34(7):1318?1322.SI Weijian,LIN Qingqing.Estimation of the number of signals based onCharacteristic subspace projection[J].Systems Engineering and Electronics,2012,34(7):1318?1322.

[12]徐振海,王雪松,肖順平,等.極化域?空域聯合譜估計[J].國防科技大學學報,2004,26(3): 63?67.XU Zhenhai,WANG Xuesong,XIAO Shunping,et al.Joint spectrum estimation of polarizational and spatial domains[J].Journal of National University of Defense Technology,2004,26(3): 63?67.

[13]TAYEM N,KWON H M.Azimuth and elevation angle estimation with no failure and no eigen decomposition[J].Signal Processing,2006,86(1): 8?16.

(編輯 陳燦華)

A source number estimation method using polarization sensitive arrayCharacteristic

WU Na,SI Weijian,JIAO Shuhong,WU Di
(College of Information andCommunication Engineering,Harbin Engineering University,Harbin150001,China)

Abstract:Considering the source number estimation problem of multi-parameter joint estimation based on polarization sensitive array,a new source number estimation algorithm was presented based on feature eliminated process.Firstly,the method performed eigenvalue decomposition(EVD)on theCovariance matrix of data vector which received by polarization sensitive array,the number of eigenvalues which was obtained was twice as much as the array element number,and then the eigenvalues were made in descending order,where the subspace spanned by the eigenvectorsCorresponded to the last half eigenvalues was included in the noise subspace,and this feature was used toConstruct a projection matrix.Secondly,newCovariance matrixes were reconstructed by feature eliminated process,thenCalculate the projection of the newCovariance matrixes on the projection matrix.Finally,the number of source was estimated according to theCriterion functionConstructed by the projection results.The results show that the angle interval and polarization angle interval effect the performance of the proposed algorithm.The proposed algorithm is more effective than theCommon GDE method.

Key words:polarization sensitive array? feature eliminated process? projection matrix? source number estimation

中圖分類號：TN911

文獻標志碼：A

文章編號：1672?7207(2016)01?0130?06

DOI:10.11817/j.issn.1672-7207.2016.01.019

收稿日期：2015?01?10；修回日期：2015?03?10

基金項目(Foundation item)：中央高校基本科研業務費資助項目(HEUCF130804)(Project(HEUCF130804)supported by the Fundamental Research Fund for theCentral Universities)

通信作者：司偉建，博士，研究員，從事寬帶信號處理、檢測與識別及高分辨高精度測向技術研究；E-mail: swj0418@263.net