基于觀測器的有限時間收斂的滑模導引律設計

周慧波，宋申民， 宋俊紅(.哈爾濱工業大學 控制理論與制導技術研究中心，黑龍江 哈爾濱，5000；2.哈爾濱師范大學 數學科學學院，黑龍江 哈爾濱，50009)

?

基于觀測器的有限時間收斂的滑模導引律設計

周慧波1,2，宋申民1， 宋俊紅1
(1.哈爾濱工業大學 控制理論與制導技術研究中心，黑龍江 哈爾濱，150001；2.哈爾濱師范大學 數學科學學院，黑龍江 哈爾濱，150009)

摘要：針對平面內彈目相對運動的末制導問題，考慮影響制導性能的目標機動和彈體動態延遲特性2個主要因素，設計漸近收斂和有限時間收斂的2種滑模導引律。選取具有動態滑模變量的線性滑模面，設計漸近穩定的滑模導引律。進一步在動態滑模變量的基礎上，選取具有有限時間收斂特性的線性滑模面，設計有限時間收斂的滑模導引律。在導引律實現過程中，利用非齊次干擾觀測器對系統未知擾動進行跟蹤估計。在目標進行2種機動情況下，選取不同的動態延遲參數。研究結果表明：數值仿真分別驗證了所設計的2種滑模導引律的有效性和可實現性。

關鍵詞：有限時間收斂；自動駕駛儀；滑模面；觀測器；導引律

傳統的制導律在目標非機動或機動程度不大的情形下，是一種十分有效的制導律。但隨著戰場態勢的復雜多變以及目標機動能力的提升，目標為進行有效規避，通常會在導彈發射后特別是在導彈制導末端突然進行大機動。在這種情形下，仍采用傳統制導律的導彈其控制量會瞬間飽和，從而導致制導時間增長、命中精度下降。同時導彈制導系統本身就是存在參數不確定性和時變的復雜非線性系統，因此用傳統的設計方法來進一步提升導彈末制導性能有很大的困難。為此需要提出一種適用于自尋的制導導彈的適應性強、制導精度高、響應速度快的新型制導律。目標機動和導彈自動駕駛儀動態延遲特性是末制導過程中影響制導精度的2個主要因素[1]。目標機動的影響可以在制導律中加以補償，以提高制導精度。ZHOU等[2?4]在導引律設計過程中，通過估計目標機動的界后用開關函數來補償對制導性能的影響。但目標機動的界選取過大，易使控制過量；選取過小則易造成系統失穩。FREIDOVICH 等[5?6]要求非線性系統具有最小相位特性時，采用高增益觀測器對目標機動進行觀測。但證明穩定性是利用不變集的性質，無法直接應用到制導系統這種有限時域的控制問題中，進一步需要對觀測誤差的收斂性和系統的穩定性進行證明。姚郁等[7?8]將系統中的機動目標加速度當作不確定性并擴張成新的一階狀態，通過設計二階擴張狀態觀測器來觀測系統狀態，從而得到機動目標加速度的估計值。ZHANG 等[9]應用非線性干擾觀測器對系統中的擾動進行跟蹤估計，設計了有限時間收斂的積分滑模導引律。以上文獻中所使用的觀測器都使得觀測誤差漸近收斂到0，為此本文作者應用一種改進的非齊次干擾觀測器，對系統中的擾動進行有限時間的跟蹤估計，同時提高了跟蹤精度。導彈自動駕駛儀的動態響應過程的時間常數決定了導彈對導引律給出的過載指令的響應速度，時間常數過大導致彈體過載跟蹤制導指令滯后，在制導末端嚴重影響制導性能。因此，在導引律設計過程中，考慮導彈動態延遲特性的影響具有現實的工程意義。目前針對導彈的動態延遲特性，主要的研究方法有動態面法[10]、反步法[11]，或者是在導引律設計中直接考慮彈體動態特性的影響[9,12]。隨著滑模控制理論的發展，滑模控制在制導控制系統[1?3,12?16]設計中得到了十分廣泛的應用。滑模控制的最好優勢是該方法對外界干擾和參數不確定性具有很強的魯棒性。在普通的滑模變結構控制的設計中，會選擇一個線性的滑動模態超曲面，使得系統的狀態在到達滑動模態時跟蹤誤差會漸近的收斂到 0。而控制理論界的學者一直在不斷地追求如何建立反饋控制系統的有限時間穩定性分析方法，并取得了一定的成果[2,9,13,16?18]。終端滑模控制方法實現了系統狀態的有限時間收斂[17?18]，但終端滑模面較線性滑模面形式復雜，且在遠離平衡點時收斂速度變慢，而趨近平衡點時易出現奇異現象。SHTESSEL等[19]提出了一種滑模變量動態法，可使系統狀態及其導數在有限時間內收斂到 0。本文作者受此啟發結合線性滑模面與滑模變量動態法的優點，分別設計漸近收斂和有限時間收斂的導引律。在導引律實現過程中，應用一種非齊次干擾觀測器，對系統中的目標總擾動進行有限時間的跟蹤估計。最后，數值仿真結果表明，所應用的觀測器能在有限時間內估計出目標總擾動。在目標進行高速機動時所設計的導引律能高精度地攔截目標。

1　問題描述

考慮攔截平面內的彈目相對運動，導彈與目標均視為質點，分別用M，T表示。它們的連線即為視線，如圖1所示。

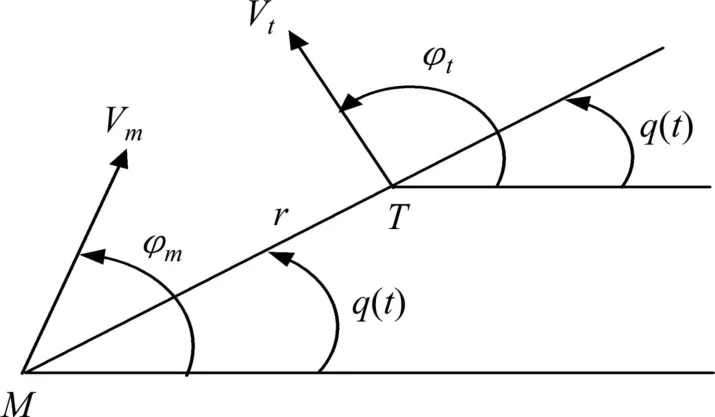
圖1　導彈和目標相對運動幾何關系Fig.1　Relative motion geometry of missile and target

由圖1可以導出如下微分方程描述[20]：

對式(2)關于時間求一階導數，可得：

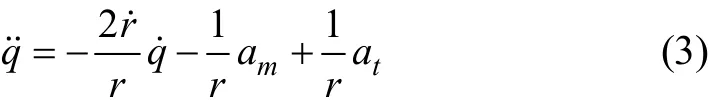
如果導彈飛行控制系統的自動駕駛儀動力學模型為一次單級慣性的，即為

其中：τ 為導彈自動駕駛儀時間常數；u 為提供給導彈自動駕駛儀的制導指令加速度。

在末制導過程中，由于受到過載能力的限制，導彈和目標實際所能提供的最大側向加速度是有限的。同時受到導引頭角跟蹤系統的功率、接收機過載等因素的限制，導引頭存在最小作用距離 r0，當彈目相對距離小于或等于 r0時，制導回路斷開[6]。記末制導開始時刻為0，不失一般性制導過程滿足如下假設。

假設1存在常數 Am＞0，At＞0，A1＞0，A2＞0使得

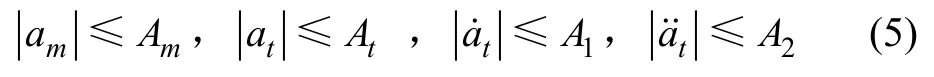
假設2 系統(3)中的時變參數 r(t)滿足

2 有限時間控制

定義1[21]考慮非線性系統

其中，f:U0×R→ Rn在 U0×R 上連續，而 U0是原點x=0的一個開鄰域。系 統的平衡點x=0(局部)有限時間收斂，是指對任意初始時刻 t0給定的初始狀態x(t0)=x0∈U，存在一個依賴于x0的停歇時間，使得式(7)以 x0為初始狀態的解 x(t)=?(t? t0,x0)有定義(可能不唯一)，并且

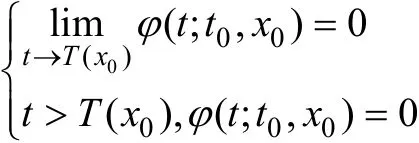
及當 t∈[t0,T(x0))時，?(t? t0,x0)∈U/{0}。另外，此系統的平衡點 x=0(局部)有限時間穩定，是指它是Lyapunov 穩定和在原點的一個鄰域 U?U0里有限時間收斂。若 U=Rn，則原點是全局有限時間穩定的平衡點。

定義2[21]令 f(x): Rn→ Rn為向量函數。若對任意的ε ＞0，存在(r1,r2,L ,rn)∈Rn，使得 f(x)滿足

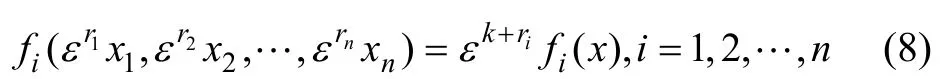
其中，ri＞0(i=1,2,L ,n)，k≥ ?max{ri, i=1,2,L,n }，則稱 f(x)關于(r1,r2,L,rn)具有齊次度k。若 向量函數f(x)是齊次的，則系統 x&= f(x)為齊次系統。

引理1[21]假定系統 x&=f(x),(x∈Rn)關于擴張系數(r1,r2,L,rn)是k＜0次齊次的，f連續并且x=0是它的漸近穩定的平衡點，則系統的平衡點是全局有限時間穩定的。

引理2[22](LaSalle不變原理)假定系統= f(x)，其中，f: D → Rn是從定義域 D ?Rn到 Rn上的局部Lipschitz映射。設 ω? D是該系統方程的一個正不變緊集，V(x): D →R 是連續可微的函數，并且在Ω內滿足(x)≤ 0。設 M是Ω內滿足(x)=0的所有點的集合，M ′是M內的最大不變集。那么，當t →∞ 時，始于Ω內的任意解都將趨于 M ′。

3 導引律的設計與實現

3.1導引律的設計

定義 x1=，x2=，則制導方程(3)可以寫為

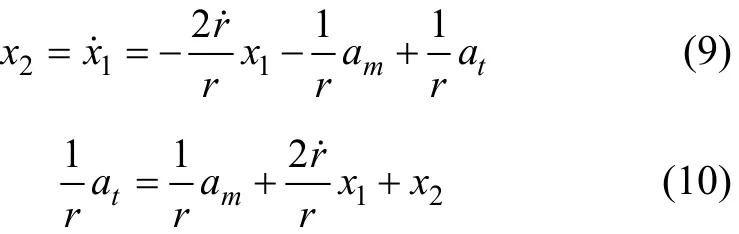
對式(9)求導，可得

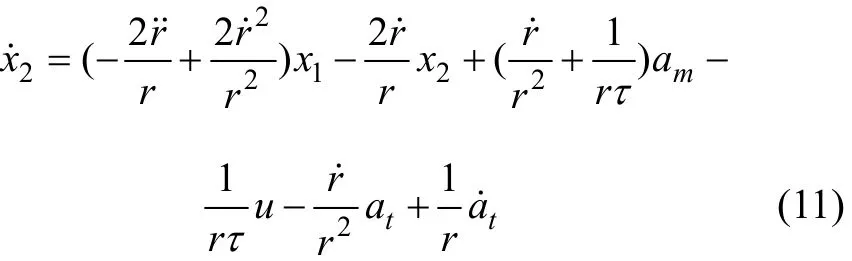
將式(10)代入式(11)，整理得

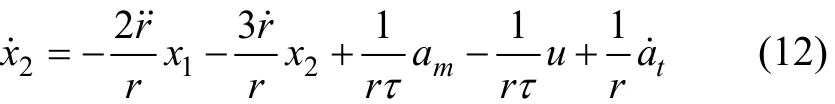
令

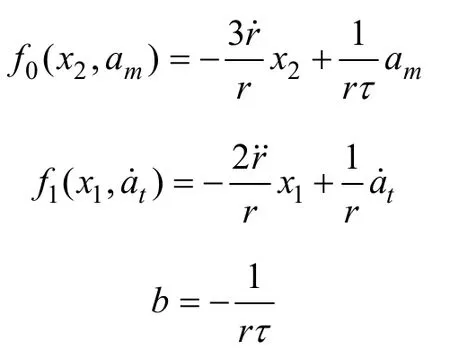
由式(9)和式(12)，整理得

對系統(13)選取線性滑模面

式中：參數k0＞0。對式(14)求導，可得

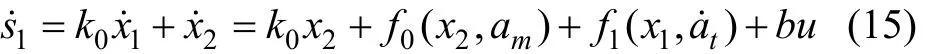
受SHTESSEL等[19]的啟發，選取

結合式(15)和式(16)，設計導引律

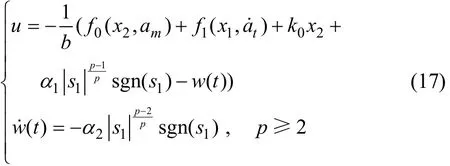
定理1針對二維平面內彈目相對運動的制導系統(13)，通過選取線性滑模面(14)，設計導引律(17)，使得系統(13)在自動駕駛儀存在一階時延的情況下，視線角速率漸近收斂到0，確保導彈精確命中目標。

證明 選取Lyapunov函數

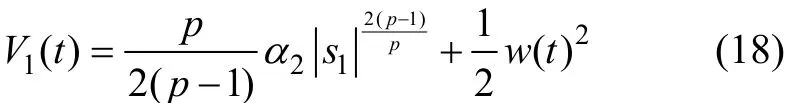
對式(18)求導并將式(15)和式(17)代入可得

導引律式(17)可確保制導系統中的視線角速率漸近收斂到 0，而有限時間收斂一直是控制界學者所追求的。為改善在線性滑模面上的性能，使其視線角速率在有限時間內收斂到0，進一步選取滑模面為

對式(20)求導，可得

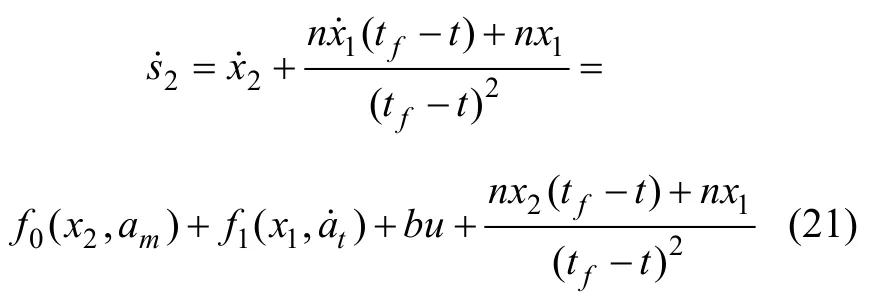
通過式(21)設計導引律

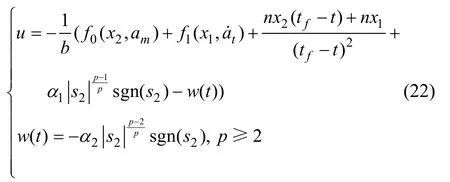
定理2針對二維平面內彈目相對運動的制導系統式(13)，通過選取線性滑模面式(20)，設計導引律式(22)，使得系統式(13)在自動駕駛儀存在一階時延的情況下，視線角速率能夠在有限時間內收斂到0。

證明 將導引律式(22)代入式(21)可得

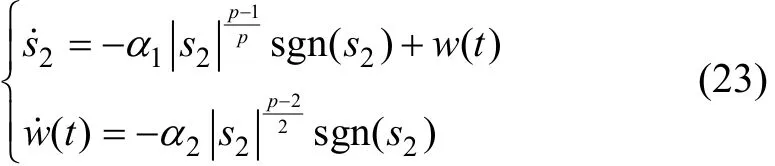
對式(23)選取Lyapunov函數

3.2導引律的實現

考慮一階的SISO非線性系統式(25)表示沿系統軌線的滑模動態特性。s=0定義了系統在滑模面上的運動，u ∈ R 為連續的控制輸入，g(t)為充分光滑的不確定函數。控制的目的是設計連續的控制u，使得s和s& 在有限時間內趨于0。

若滑模變量 s 和控制輸入 u 能實時獲得，g(t)是m?1次可微，gm ?1(t)具有已知的 Lipschitz 常數 L。基于Levant提出的非齊次微分器[23]，李 鵬[24]提出了非齊次干擾觀測器以加快暫態過程，形式如下：

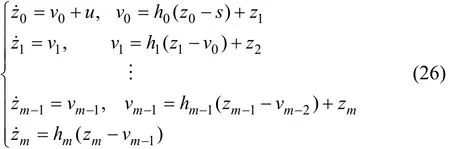
式(26)中hi為下列形式的函數

其中：λi，μi＞0，i=0,1,L,m。

引理 3[24]假設系統式(25)中的 s(t)和 u(t)可測且不存在量測噪聲，參數 λi和 μi在逆序上充分大，則經歷有限時間的暫態過程后，下列方程成立

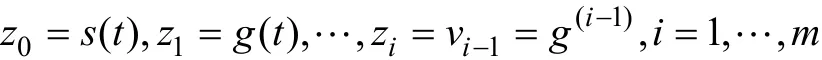
為此，對 系統式(15)和式(21)的總擾動進行有限時間內的跟蹤估計，選取非齊次干擾觀測器形式為

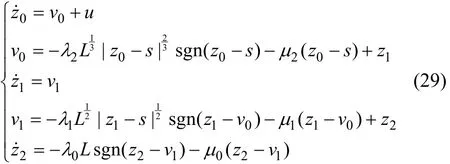
則在有限時間內

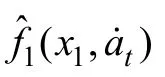
從而由定理1和定理2，系 統式(13)可實現的導引律分別為式(31)和式(32)。

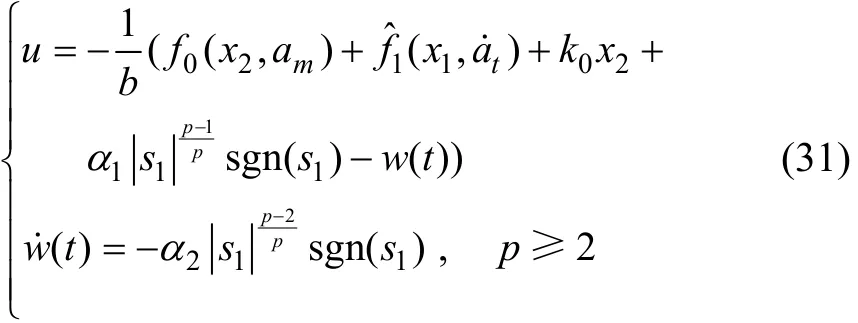
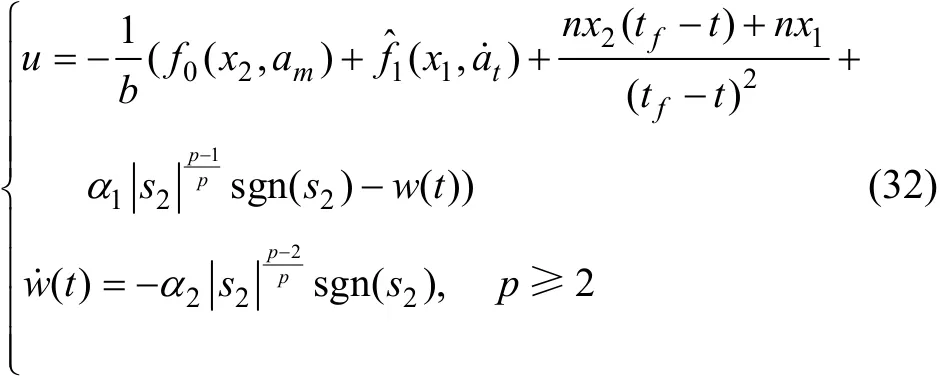
在式(31)和式(32)中，當p=2時將其分別代入式(15)和式(21)中，可得形式為

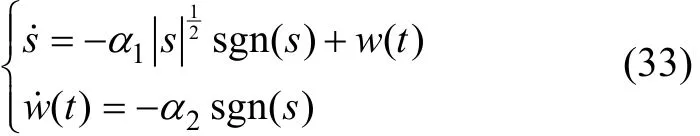
式(33)就是super-twisting算法，但它是非光滑的，滑模面在趨于0的過程中在滑模面為零的兩側抖振，影響制導性能。通過仿真可進一步看出當p＞2時，所設計的導引律性能更好。

4　數值仿真

設某型導彈在某一高度上飛行，馬 赫數為3.5，音速為295.07 m/s，目標的飛行速度為900 m/s，目標和導彈在鉛垂面內運動。

設末制導初始時刻，導彈在慣性系下的位置為xm(0)=0.5 km，ym(0)=16 km，導彈和目標的初始彈道偏角為 φm(0)=φt( 0)=10°，目標的初始位置為xt(0)=1.5 km，yt(0)=16.5 km，導引頭中斷尋的制導距離為r0=100 m。觀測器參數為λ0=1.1；λ1=1.5；λ2=2；μ1=6；μ2=8；L=10 和 g=9.8 m/s2。 假定從末制導開始時刻起，目標分2種情況機動。

情況1：目標在法向上做 at=4 gcos(π t/4)的余弦機動。在導引律式(31)和導引律式(32)中，參數α1=2；α2=3；k0= n =2和 τ=0.5。當p=2,3,4,5時，2 種方法對應的視線角速率、滑模面、導彈法向過載和觀測器誤差估計曲線分別如圖2～5所示，其 中：標記(a)的為導引律式(31)所描繪的曲線，標記(b)的為導引律式(32)所描繪的曲線，相應的脫靶量和命中時間如表1所示。

表1　脫靶量和命中時間Table1　Miss distances and interception time

由表1可見：在 p 取不同值時，導引律式(31)相應的制導結束時間基本一致，脫靶量也相差不大。導引律式(32)(相應的制導結束時間和脫靶量)比導引律式(31)的都小，總體而言所設計的導引律都能精確命中目標。

圖2所示為視線角速率的變化規律，在余弦機動情況下，視線角速率變化曲線快速收斂到 0，這保證了導彈能精確命中目標。只是圖 2(a)中視線角速率比圖 2(b)中的視線角速率提前到達穩定狀態，圖 2(b)中的視線角速率收斂較緩慢，特別在p=2時，相應的視線角速率變化曲線有輕微抖動。因此由圖3～5可見：p=2 時相應的滑模面曲線、導彈法向過載曲線和觀測器跟蹤誤差曲線都出現抖動，尤其是擾動估計誤差曲線，這造成了制導性能下降，所以，當 p=2 時，即super-twisting 算法設計的導引律比 p＞2 時所設計的導引律較差。同樣由圖3～5可見：當p＞2時，另外3種取值的滑模面曲線和擾動估計誤差曲線平穩、 光滑、快速的收斂到 0，這也說明所選取的非齊次干擾觀測器的有效性。而導彈法向過載曲線也快速穩定到一個固定值附近，且過載較小。由圖3可見：收斂到滑模面時相應曲線在最初圖 3(a)比圖 3(b)的值要大些，但很快都收斂到 0。相應的由圖4可見：導彈法向過載曲線在最初圖 4(a)比圖 4(b)的值也要大些，這說明導引律式(32)的總體性能較導引律式(31)的優越。

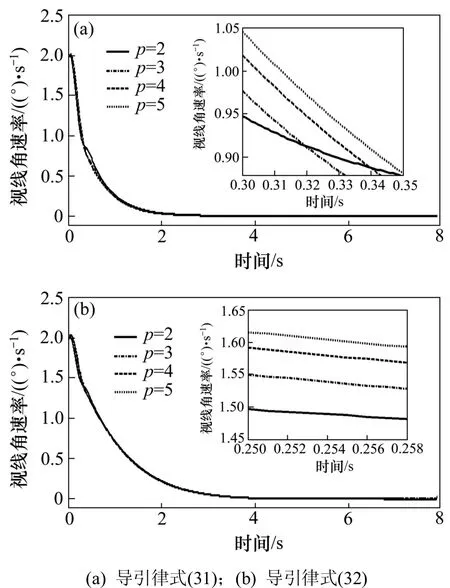
圖2視線角速率Fig.2Line-of-sight angle rate

圖3　滑模面Fig.3　Sliding mode surface

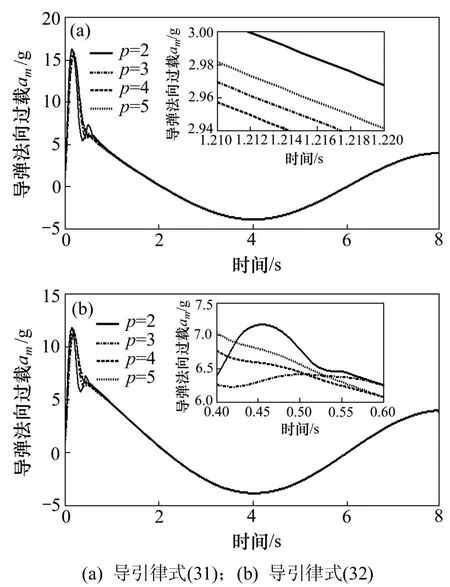
圖4導彈法向過載Fig.4Missile normal acceleration

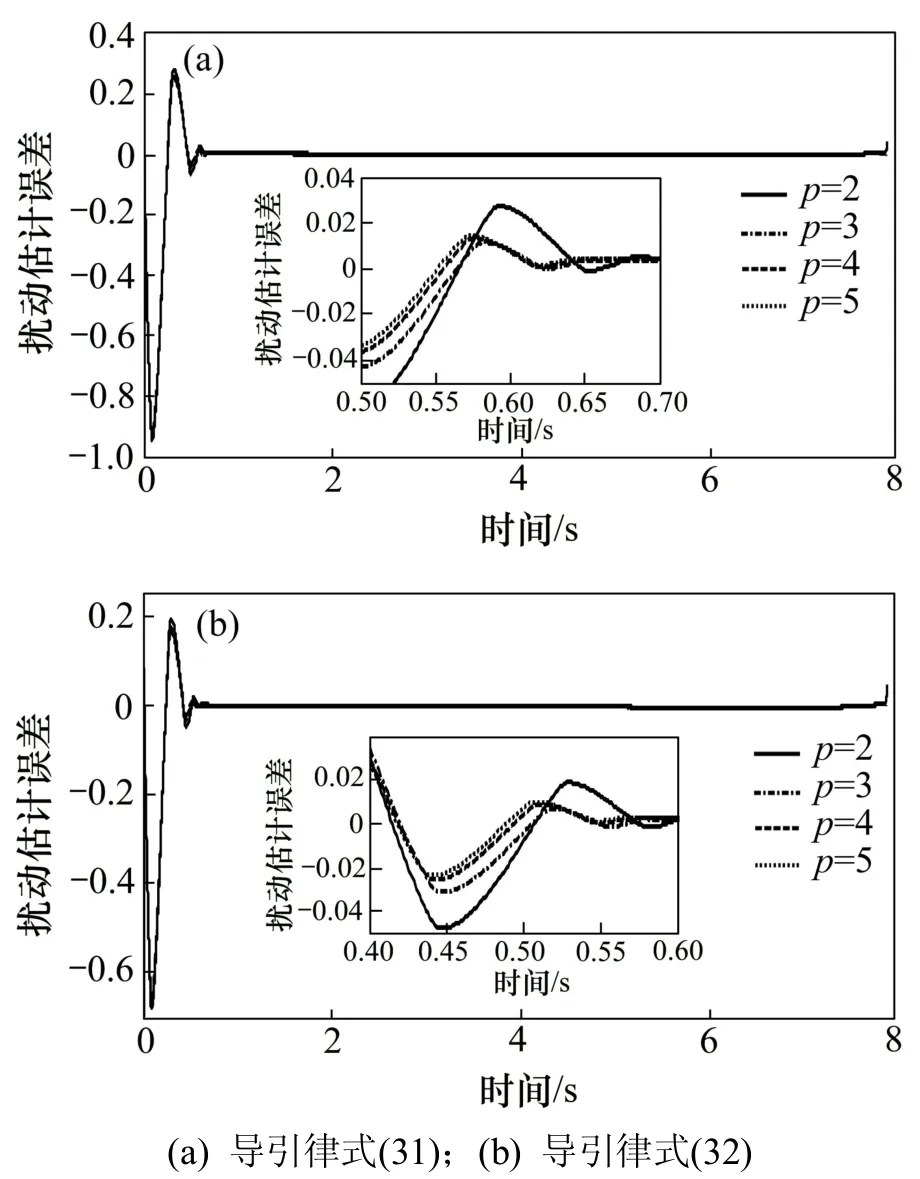
圖5　觀測器誤差Fig.5　Observer error

情況 2: 目標在法向上做 at=9 gsin(π t/4)的正弦大機動。在導引律式(31)(記為 am1)和導引律式(32)(記為 am2)中僅取p=3，τ =0.5 和 τ=0.8，其余參數同前。在大機動情況下導引律 am1和導引律 am2與 p=2 時的super-twisting 算法分別記為導引律 am11(在普通線性滑模面上)和 am22(在有限時間收斂的線性滑模面上)在選取2個不同的動態時延常數時，所描繪的視線角速率、滑模面和法向過載曲線如圖6～8所示，脫靶量如表2所示。

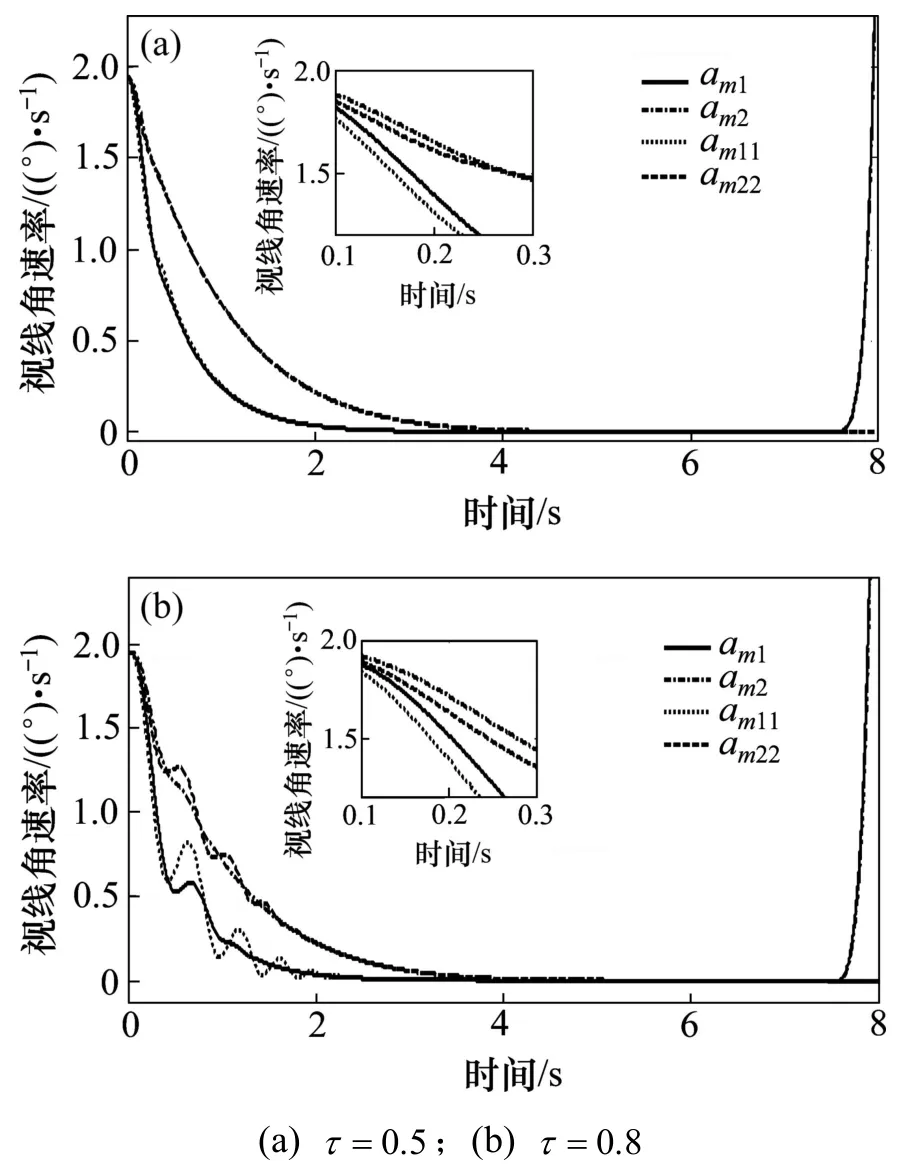
圖6　視線角速率Fig.6　Line-of-sight angle rate

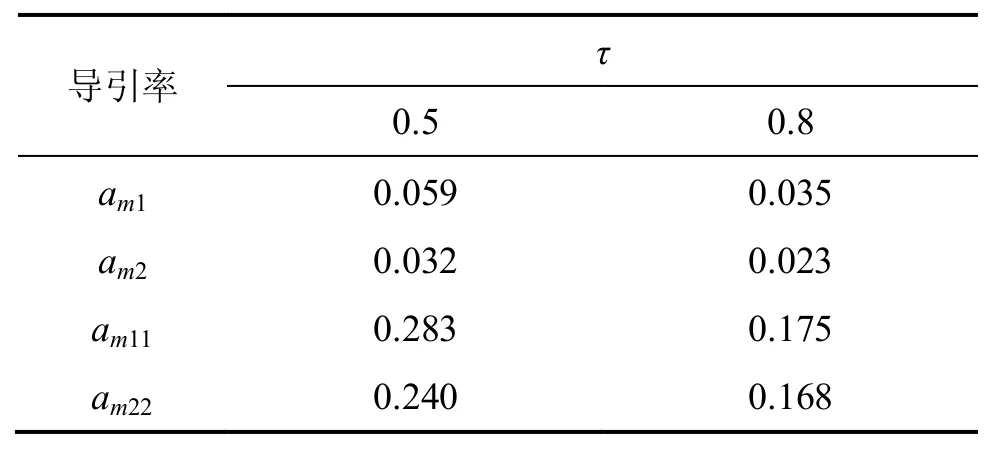
表2脫靶量Table1　Miss distances　m

由表2 可見：選取 τ=0.5 和 τ=0.8 時，4 種導引律的脫靶量都滿足制導精度要求。從圖 6(a)可見：4種導引律的視線角速率曲線相差不大。但當 τ=0.8時，由圖 6(b)可見：導引律 am11和 am22的視線角速率曲線出現抖動，時間持續到3s。對應的滑模面和法向過載曲線圖7(a)和圖8(a)也差距不大。但圖7(b)和圖8(b)的曲線都出現相應的抖動。由此可見，導引律 am11和 am22與導引律 am1和 am2對應進行比較，制導性能變差。同時也說明目標大機動方式下，導彈在取不同的延遲參數時，導引律 am1和 am2具有良好的魯棒性和普適性。

圖7　滑模面Fig.7　Sliding mode surface

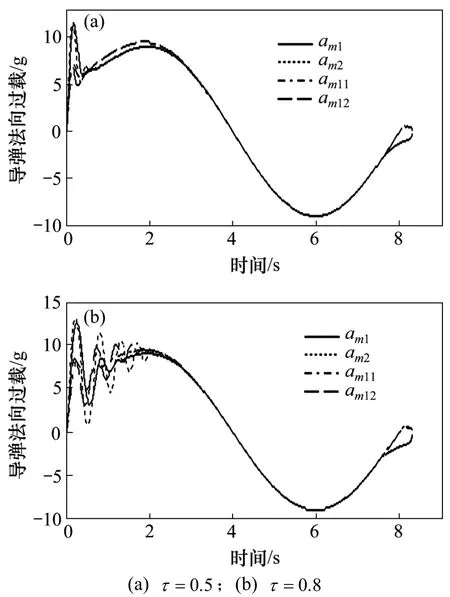
圖8　導彈法向過載Fig.8　Missile normal acceleration

5 結論

1)選取普通的線性滑模面與滑模變量動態方法結合，設計了指數收斂的非線性滑模導引律。

2)選取有限時間收斂的線性滑模面與滑模變量動態方法結合，設計了有限時間收斂的非線性滑模導引律。

3)在導引律實現過程中，為避免對系統中的總擾動進行有界估計而應用非齊次干擾觀測器，對系統中的總擾動進行有限時間內的快速跟蹤估計。該導引律克服了導彈控制系統的動態延遲特性和目標擾動對制導精度的影響。

4)在目標進行余弦機動和大的正弦機動時，通過選取不同的時延參數，進行多組仿真驗證了所設計導引律的有效性和可實現性。導引律結構簡單，利于工程實現。

參考文獻：

[1]馬克茂,馬杰.機動目標攔截的變結構制導律設計與實現[J].宇航學報,2010,31(6):1589?1593.MA Kemao,MA Jie.Design and implementation of variable structure guidance law for maneuvering target interception[J].Journal of Astronautics,2010,31(6):1589?1593.

[2]ZHOU D,SUN S,TEO K L.Guidance laws with finite timeConvergence[J].Journal of Guidance,Control,and Dynamics,2009,32(6):1838?1846.

[3]RAO S,GHOSE D.Terminal impact angleConstrained guidance laws using variable structure systems theory[J].IEEE Transactions onControl Systems Technology,2013,21(6): 2350?2359.

[4]SHIMA T.Intercept-angle guidance[J].Journal of Guidance,Control,and Dynamics,2011,34(2): 484?492.

[5]FREIDOVICH L B,KHALIL H K.Performance recovery of feedback-linearization-based designs[J].AutomaticControl,IEEE Transactions on,2008,53(10): 2324?2334.

[6]馬克茂,賀風華,姚郁.目標機動加速的估計與導引律實現[J].宇航學報,2009,30(6): 2213?2219.MA Kemao,HE Fenghua,YAO Yu.Estimation of target maneuver acceleration and guidance law implementation in homing terminal guidance[J].Journal of Astronautics,2009,30(6): 2213?2219.

[7]姚郁,王宇航.基于擴張狀態觀測器的機動目標加速度估計[J].系統工程與電子技術,2009,31(11): 2682?2684,2692.YAO Yu,WANG Yuhang.Acceleration estimation ofmaneuvering targets based on extended state observer[J].Systems Engineering and Electronics,2009,31(11): 2682?2684,2692.

[8]ZHENG Zhu,DONG Xu,LIU Jingmeng,et al.Missile guidance law based on extended state observer[J].IEEE Transactions on Industrial Electronics,2013,60(12): 5882?5891.

[9]ZHANG Zhu,LI Shihua,LUO Sheng.Composite guidance laws based on sliding modeControl with impact angleConstraint and autopilot lag[J].Transactions of the Institute of Measurement andControl,2013,35(6): 764?776.

[10]曲萍萍,周荻.考慮導彈自動駕駛儀二階動態特性的三維導引律[J].航空學報,2011,32(11): 2096?2105.QU Pingping,ZHOU Di.Three-dimensional guidance law accounting for second-order dynamics of missile autopilot[J].Acta Aeronautica et Astronautica Sinica,2011,32(11): 2096?2105.

[11]孫勝,張華明,周荻.考慮自動駕駛儀動特性的終端角度約束滑模導引律[J].宇航學報,2013,34(1): 69?78.SUN Sheng,ZHANG Huaming,ZHOU Di.Sliding mode guidance law with autopilot lag for terminal angleConstrained trajectories[J].Journal of Astronautics,2013,34(1): 69?78.

[12]佘文學,周軍,周鳳岐.一種考慮自動駕駛儀動態特性的自適應變結構制導律[J].宇航學報,2003,24(3): 245?249.SHE Wenxue,ZHOU Jun,ZHOU Fengqi.An adaptive variable structure guidance lawConsidering missile’s dynamics of autopilot[J].Journal of Astronautics,2003,24(3): 245?249.

[13]ZHANG Yunxi,SUN Mingwei,CHEN Zhengqiang.Finite-timeConvergent guidance law with impact angleConstraint based on sliding-modeControl[J].Nonlinear Dynamics,2012,70(1): 619?625.

[14]KUMAR S R,RAO S,GHOSE D.Sliding-mode guidance andControl for all-aspect interceptors with terminal angleConstraints[J].Journal of Guidance,Control,and Dynamics,2012,35(4):1230?1246.

[15]HARL N,BALAKRISHNAN S N.Impact time and angle guidance with sliding modeControl[C]//AIAA Guidance,Navigation,andControlConference,Chicago,lllinois,2009:1?22.

[16]YAMASAKI T,BALAKRISHNAN S N,TAKANO H,et al.Second order sliding mode-based intercept guidance with uncertainty and disturbanceCompensation[C]//AIAA Guidance,Navigation,andControl(GNC)Conference.Boston,MA: American Institute of Aeronautics and Astronautics,2013:1?17.

[17]YU X H,MAN Z H.Fast terminal sliding-modeControl design for nonlinear dynamical systems[J].IEEE Transactions onCircuits and Systems I: Fundamental Theory and Applications,2002,49(2): 261?264.

[18]FENG Y,YU X,MAN Z.Non-singular terminal sliding modeControl of rigid manipulators[J].Automatica,2002,38(12): 2159?2167.

[19]SHTESSEL Y B,SHKOLNIKOV I A,LEVANT A.Smooth second-order sliding modes: Missile guidance application[J].Automatica,2007,43(8):1470?1476.

[20]周荻.尋的導彈新型導引規律[M].北京: 國防工業出版,2002:14?15.ZHOU Di.New guidance laws for homing missile[M].Beijing: National Defense Industry Press,2002:14?15.

[21]洪奕光,程代展.非線性系統的分析與控制[M].北京: 科學出版社,2005:159?161.HONG Yiguang,CHENG Daizhan.Analysis andControl of nonlinear systems[M].Beijing: Press of Science,2005:159?161.

[22]KHALIL H K.Nonlinear systems[M].The Third Edition.New York: Prentice-Hall,2001: 89?93.

[23]LEVANTA.Non-homogeneousfinite-time-convergent differentiator [C]//Decision andControl,2009 held jointly with the 2009 28thChineseControlConference.Proceedings of the 48th IEEEConference on.Shanghai: IEEE,2009: 8399?8404.

[24]李鵬.傳統和高階滑模控制研究及其應用[D].長沙: 國防科技大學機電工程與自動化學院,2011: 85?86.LI Peng.Research and application of traditional and higher-order sliding modeControl[D].Changsha: National University of Defense Technology.Mechatronic Engineering and Automation,2011: 85?86.

(編輯 羅金花)

Design of an observer-based sliding mode guidance law with finite timeConvergence

ZHOU Huibo1,2,SONG Shenmin1,SONG Junhong1
(1.Center forControl Theory and Guidance Technology,Harbin Institute of Technology,Harbin150001,China? 2.School of Mathematical Sciences,Harbin Normal University,Harbin150009,China)

Abstract:Considering the terminal guidance issue that the missile and the target were relatively moving in a plane,two major factors of the target’s maneuvering and missile’s dynamic delayCharacteristics wereConsidered.Then,two sliding mode guidance laws with asymptoticConvergence and finite timeConvergence were respectively designed.Firstly,selecting the linear sliding manifold with dynamic sliding mode variable,a sliding mode guidance law with asymptotic stability was proposed.After that,a linear sliding mode manifold with finite timeConvergence was further selected on the basis of dynamic sliding mode variable,and a sliding mode guidance law with finite timeConvergence was presented.In the process of implementing the guidance law,an inhomogeneous disturbance observer was employed to estimate the unknown disturbance of the system.Finally,twoCases for the different target acceleration and selecting different dynamic delay parameters wereConsidered.The results show that simulationComparison results are provided to demonstrate the effectiveness and the realizability of the proposed two sliding mode guidance laws from.

Key words:finite timeConvergence? autopilot? sliding mode surface? observer? guidance law

中圖分類號：V448.133

文獻標志碼：A

文章編號：1672?7207(2016)01?0091?09

DOI:10.11817/j.issn.1672-7207.2016.01.014

收稿日期：2015?01?01；修回日期：2015?03?01

基金項目(Foundation item)：國家自然科學基金創新群體項目(61021002)；黑龍江省自然科學基金資助項目(A201410)(Project(61021002)supported by the National Natural Science Foundation ofChina? Project(A201410)supported by the Natural Science Foundation of Heilongjiang Province ofChina)

通信作者：周慧波，博士，副教授，從事飛行器制導與控制研究；E-mail: zhouhub0606@sina.com