基于顯式動力學有限元法的汽車盤式制動器仿真研究

成林，王谷娜，王茂美（北京電子科技職業學院，北京 100176）

?

基于顯式動力學有限元法的汽車盤式制動器仿真研究

成林，王谷娜，王茂美
（北京電子科技職業學院，北京 100176）

摘要：根據制動盤與摩擦片的實際幾何尺寸，建立制動工況下三維瞬態溫度場-應力場仿真的計算模型。在考慮制動盤與摩擦片之間摩擦特性的基礎上，運用有限元軟件 ABAQUS 中的顯式動力學模塊，對盤式制動器的制動過程進行了動態的模擬，揭示了制動過程中制動盤瞬態溫度場-應力場的分布規律，發現二者之間存在著耦合關系，二者隨制動時間呈現周期性變化。

關鍵詞：顯式動力學；有限元法；盤式制動器；仿真研究

10.16638/j.cnki.1671-7988.2016.05.003

CLC NO: U463.51+2Document Code: AArticle ID: 1671-7988 (2016)05-09-04

前言

制動器廣泛應用于飛機、火車、汽車等各類交通工具中，是一種交通安全裝置。盤式制動器制動因數與摩擦系數成線性關系，具有制動性能穩定，力矩容量大和有利于程序化控制等突出的優點，已成為目前最先進的制動裝置之一。

圖1　盤式制動器三維模型

制動器制動過程中的溫度場-應力場的變化規律對制動性能有很大影響，摩擦片各種形式的損壞的主要原因是摩擦所產生的熱量超過了摩擦材料的極限熱容量[1]。摩擦熱導致摩擦材料發生熱降解、粘結劑氣化，摩擦因數發生變化，制動性能降低，出現熱衰退現象；也使金屬對偶件發生局部材料的相變與熱變形，出現局部熱點。局部熱點的出現導致制動壓力不均勻分布的進一步發展，這反過來又促進局部溫度進一步升高，使制動器出現熱彈性不穩定現象。在熱應力作用下很容易造成材料的熱衰退和破壞，產生初始裂紋并導致表面刮削現象加劇[2]。而熱彈性失穩的出現，使得制動器摩擦振動與噪聲加大。由于摩擦熱的產生與接觸壓力的大小直接相關，而溫度分布的不均勻性導致物體的熱變形差異又直接影響接觸狀態或接觸壓力，接觸狀態的改變反過來影響摩擦熱流輸入強度[3]。可見摩擦制動器的熱問題是應力場與溫度場耦合問題。

本文按照制動盤與摩擦片的實際幾何尺寸，把盤、片作為一個整體，建立了制動工況下三維瞬態溫度場-應力場統一的有限元模型，利用顯式動力學有限元法，仿真了制動器的制動過程，并考慮了摩擦熱流在盤片之間的耦合問題，以及熱源移動速度可變效應對制動盤熱應力分布的影響。

1、顯式動力學有限元法

傳統的有限元法在算法上屬于靜態隱式算法。求解中每個時間步都要重新計算大型非線性剛度矩陣，并進行反復迭代以獲得收斂解。需要較長的計算時間和較大的存貯空間。限于當前計算機的速度與容量，求解高度非線性的盤式制動器摩擦生熱問題一直局限于二維或較小寬厚比的三維情況。基于顯式算法的顯式動力學有限元法克服了靜態隱式有限元法收斂困難，計算時間長，存儲空間大，接觸與摩擦難于處理等的缺陷，能有效處理大規模接觸和高度非線性問題[4]。顯式動力學有限元法的基本方程為：

式中M表示質量矩陣；C表示阻尼矩陣；F表示內力矢量；R表示外載荷矢量；分別表示節點速度和加速度矢量。

通常采用中心差分法求解式（1.1）。tn時刻的離散速度和加速度中心差分公式分別為：

式中u表示位移。

把式（1.2）、（1.3）代入式（1.1），得到求解各離散時間點位移的遞推公式為：

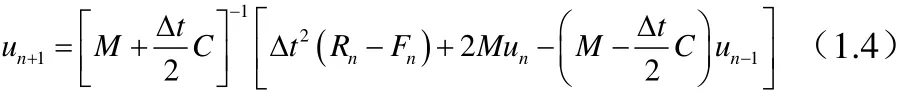
中心差分法是一種顯式算法，它要求條件穩定。當利用它求解具體問題時，時間步長必須小于由該問題求解方程性質所決定的某個臨界值?tmin，否則算法不穩定。

根據Courant-Friendrichs-Levy穩定性準則，臨界時間步長可由下式確定，即：

式中ωmax表示系統的最大固有頻率；L表示單元特征長度（等于單元中任意兩節點間的最小距離）；c表示材料中的聲速（與材料的性質有關）。對于三維單元，材料中的聲速為：

2、溫度場-應力場耦合問題計算模型的建立

要研究制動器工作過程中的溫度場，必須建立摩擦生熱模型，而摩擦生熱問題是一種典型的溫度場-應力場耦合問題。

2.1熱傳導模型的建立

建立熱傳導模型時，作以下假設[5]：

(1) 制動過程中，摩擦符合庫侖定律，摩擦因數保持不變。

(2) 制動壓力均勻作用于摩擦片，制動器內外兩側的片所產生的熱負荷相等，即溫度場-應力場對稱于盤中心平面，因此只需考慮盤的一側。

(3) 為解決摩擦熱流在盤片之間的分配問題，考慮摩擦熱流耦合問題。假設接觸界面為理想平面，且在接觸區域盤、片界面對應點瞬時溫度相等；這樣，摩擦熱流密度q( x , y , t )根據界面的理想熱傳導和盤片的熱物理性質在盤片之間自然分配；并且考慮熱輻射影響。

(4) 不考慮材料磨損的影響，認為所有的摩擦功都轉化為摩擦熱，并且在計算時，把盤、片的熱流輸入當作邊界熱流輸入處理，則摩擦表面輸入熱流密度滿足：式中：表示摩擦表面上的比壓；μ表示摩擦因數；v( x , y , t )表示盤、片的相對移動速度。

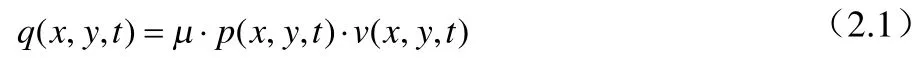
(5) 盤及片的材料為各向同性材料，由于單次緊急制動時間較短，材料熱物性參數不隨溫度變化。

根據實際情況，認為片固定不動，而盤作逆時針轉動。可得盤、片在直角坐標下的熱傳導方程：

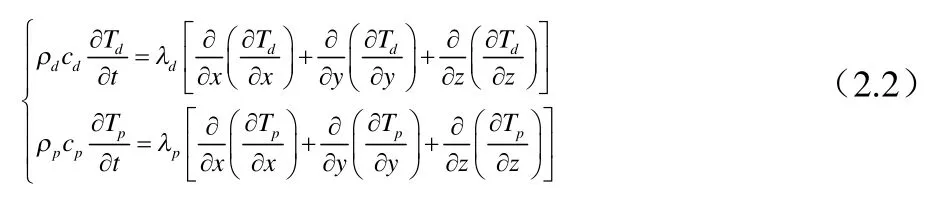
式中dρ、ρp表示盤、片的材料密度；cd、cp表示盤、片的比熱容；dλ、pλ表示盤、片的熱導率；Td、Tp表示盤、片的溫度；t表示制動時間。

制動盤的內圓側面與輪軸凸緣盤相連，又與摩擦熱流輸入區域相距較遠，對于緊急制動工況，其熱流作用時間短，該表面是絕熱的；制動盤的中心平面也是絕熱的。摩擦片的背面遠離摩擦面且與鋼背相連，是絕熱表面。

2.2熱應力的計算

首先假設材料在制動過程中只發生線彈性變形。物體由于熱膨脹只產生線應變，剪切應變為零。這種由于熱變形產生的應變可以看作是物體的初應變。計算應力時包括初應變項：

式中σ表示材料的應力矩陣；D表示材料的彈性矩陣；ε表示材料的應變矩陣；表示溫度變化引起溫度應變。

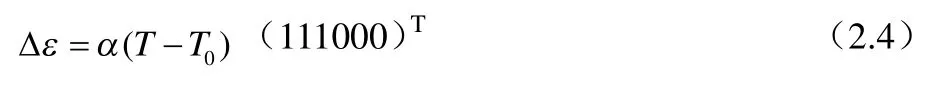
式中α表示材料的熱膨脹系數；T0表示結構的初始溫度場，假定是均勻的；T表示制動時結構的溫度場。

2.3位移邊界條件

根據實際情況，這里認為片不動，盤做逆時針轉動。由于制動壓力作用在摩擦片上，摩擦片是固結在制動鋼背上，故對摩擦片施加x，y軸兩個方向的固定約束。

根據假設條件(2)，認為盤的中心平面沿z方向軸向固定約束。

由于盤的內孔與軸相連接，故在內圓側面施加z軸方向的固定約束，而在x，y軸方向上施加預定的對應位移，為模擬制動盤的減速運動。

3、盤式制動器溫度場-應力場的耦合仿真

本文以首鋼SGA3723礦用汽車盤式制動器的結構為例，制動盤的材料為ZG1Cr13，摩擦片材料為樹脂基復合材料。計算分析所需參數見表1。總制動時間為3.0s，制動初始車速為25km/h，初始制動壓力為10MPa。

表1　材料的特性參數

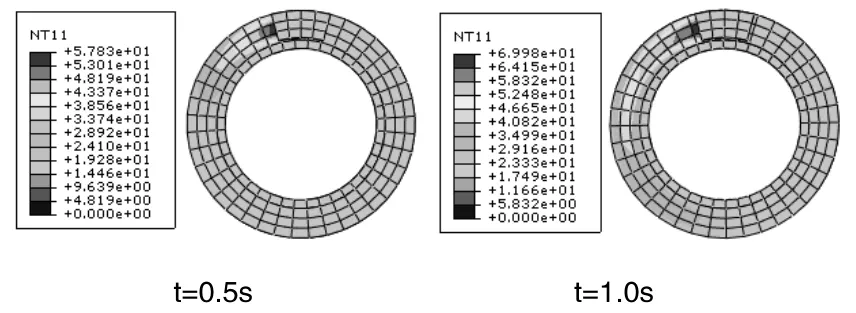
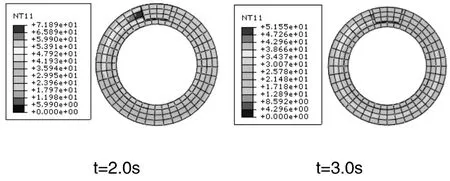
圖2　制動不同時刻溫度分布

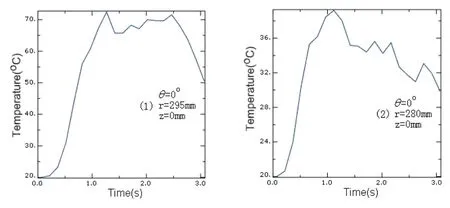
圖3　不同半徑點溫度-時間曲線

圖2為制動器持續制動3.0s時制動盤表面溫度分布圖，在t=2.0s時表面溫度達到制動中的最大值，從制動開始制動盤的溫度（初始溫度為環境溫度）一直升高，但溫度分布并不均勻。t=3.0s時制動結束，此時溫度比t=2.0s時要低一些，主要因為制動后期制動盤的速度很低，此時摩擦產生的熱流密度輸入量低于制動盤與外界的對流換熱量，因此制動盤的溫度由最大值開始下降，當到制動結束時制動盤的溫度分布接近軸對稱分布。圖3為不同半徑點溫度隨時間變化曲線，左圖最高溫度高于右圖，這是因為點（1）處的切線速度大于點（2），因此輸入的熱流密度大，溫度比較高。

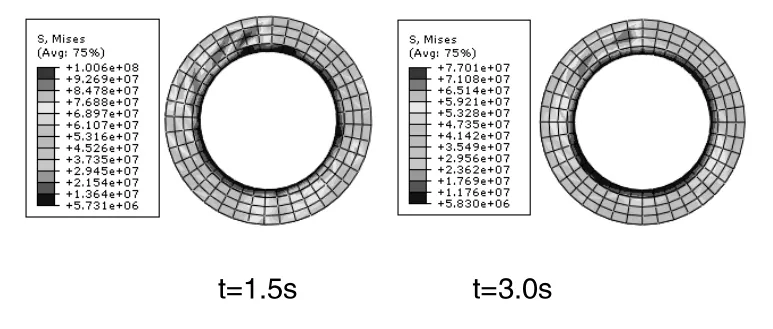
圖4　制動不同時刻應力分布

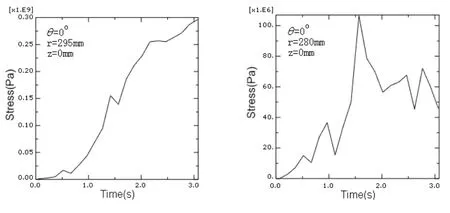
圖5　不同半徑點應力-時間曲線

從圖4和圖5可以看出，由盤內溫度分布的不均勻引起的熱應力分布是相當不均勻的。由于制動時間短，摩擦副產生熱量的速度要遠高于熱量向材料內部傳遞的熱傳導速度，制動盤摩擦接觸表面溫度高于材料內部區域的溫度，并且摩擦區域的表面溫度要高于非摩擦區域的表面溫度，從而在徑向、周向產生很大的溫度梯度。這一溫度梯度使得制動盤摩擦區域部分要向徑向和周向膨脹，

但受到非溫升的約束而不能自由進行，導致在摩擦高溫區域，其徑向和周向都產生了很大的壓應力。盤的內徑處非摩擦區域基本沒有什么溫升，產生了拉應力。同時制動盤沿半徑方向溫度變化梯度高于沿軸向的溫度變化梯度，從而導致制動盤周向應力明顯要高于徑向應力。因此，由此而產生的熱裂紋往往是沿半徑方向分布的。

4、結論

（1）本文建立了盤式制動器溫度場－應力場耦合瞬態非軸對稱有限元模型及其相關的邊界條件，所建模型充分考慮制動器實際尺寸、摩擦熱流耦合和移動熱源可變效應的影響，能較好的仿真制動器制動過程中的溫度場-應力場的動態特性。

（2）溫度及應力的最大部位出現在與摩擦片接觸的垂直中心部位，在摩擦中這些部位溫度及應力不斷升高，而制動盤內、外徑處溫升相對很小，這是因為內、外徑距摩擦區相對較遠。制動中摩擦片的溫度最大值處于摩擦區的出口靠近外徑處，這個部位是最容易磨損的部位，這與摩擦片磨損的實際情況相符合。

（3）制動器表面溫度隨制動開始迅速升高，大約在制動時間三分之二時達到最大值，然后逐漸降低，在制動結束時溫度接近軸對稱分布。

參考文獻

[1]李非雪,張文明,方湄.濕式多片制動器摩擦片溫度分布規律[J].北京科技大學學報,2001,23(6)：539～542.

[2]王亞冪,李世其,宋少云.多場耦合系統協同設計方法研究[J].機械制造,2006,44(4):34～37.

[3]周凡華,吳光強,沈浩.盤式制動器15次循環制動溫度計算[J].汽車工程,2001,23(6):411～413.

[4]劉立忠,劉相華,王國棟.軋制過程的顯式動力學有限元模擬[J].東北大學學報,2001,22(3):327～330.

[5]張立軍,司揚,余卓平.非均勻盤式制動器熱機耦合特性試驗研究[J].汽車技術,2008(6):45～49.

Simulation Study of Automobile Disc Brake Based on Dynamic Explicit Finite Element Method

Cheng Lin, Wang Gu’na, Wang Maomei
（Beijing Polytechnic, Beijing 100176）

Abstract:According to the actual geometry of brake disc and the friction plate, the simulation calculation model of three-dimensional transient temperature field and stress field under braking condition is established. Considering the friction characteristics between the brake disc and the friction plate, the dynamic simulation is used to the braking process of disc brake with explicit dynamic module of ABAQUS. The distribution rules of the brake disc transient temperature field and stress field is studied. The temperature field and stress field are coupled. The temperature field and stress field change periodically with braking time.

Keywords:Explicit dynamics; Finite element method; Disk brake; Simulation study

中圖分類號：U463.51+2

文獻標識碼：A

文章編號：1671-7988（2016）05-09-04

作者簡介：成林，博士研究生，就職于北京電子科技職業學院汽車工程學院。主要研究方向為汽車制動系統的優化設計與仿真。